# #3 Improved Training of Wasserstein GANs
https://arxiv.org/abs/1704.00028

###### tags: `論文まとめ` `GAN`

# 要旨

GANは強力な生成モデルだが，学習が不安定という弱点がある．Wasserstein GANを用いることで，学習にある程度の安定性を持たせたが，特定のダメなサンプルのみを生成してしまうことや，収束の失敗が起こることがある．これは，ディスクリミネータ(critic)に対し，リプシッツ連続の制約を満たすべく，重みのクリッピングを行っていたことに起因することが分かった．そこで，重みをクリップするのではなく，入力に対するディスクリミネータの勾配のノルムをペナルティ項として加算するという新規手法を提案した．この方法により，従来のWGANよりも学習が安定化し，様々な種類のGANに対して，さほどハイパーパラメータチューニングを施すことなく，安定して学習できることを可能にした．

# 前提知識
## Wasserstein GAN

https://arxiv.org/abs/1701.07875
上記論文にて，GANが最小にする発散は，ジェネレータのパラメータに対して連続でない可能性がある．
そこで，上論文はEarth-Mover距離(Wasserstein距離)$W(q,p)$を使用した．これは分布$q$に従って散らばった堆積物を分布$p$に移動させる最小輸送重量コストとして定義される．軽い仮定の下では，$W(q,p)$は任意点で連続で，ほとんど至る所で微分可能である．
WGANの損失関数は ***Kantorovich-Rubinstein双対性*** を用いることで以下の式のように定義できる．

$\displaystyle\min_G \max_{D \in \mathcal D} \mathbb E_{\bf x\sim\mathbb P_r}[D(\bf x)]-\mathbb E_{\bf{\tilde{x}}\sim\mathbb P_g}[D(\bf{\tilde{x}})]$

ただし$\mathcal D$は1-リプシッツ関数の集合であり，$\mathbb P_g$は$\tilde{\bf x}=G(z),z\sim p(z)$によって暗黙に定義されるモデル分布である．このような場合，最適なディスクリミネータ(この論文中では，分類を学習するわけではないのでcriticと呼んでいる)の下では，ジェネレータのパラメータの関数を最小化させることは，$W(\mathbb P_r,\mathbb P_g)$を最小化させることに等しい．

WGANの損失関数は，その入力に対する勾配がGANのそれよりも良い挙動を示すようなCritic関数をもたらすことができる．経験的に，WGANの損失関数はサンプルの質と相関関係があることが分かっている．この傾向は従来のGANには見られなかった性質である．

WGANでは，Criticがリプシッツ制約を満たすべくコンパクト空間$[-c,c]$に落とし込むようにCriticの重みをクリッピングする．この制約を満たす関数の集合は，$c$とCriticのアーキテクチャに依存する$k$に対する$k-$リプシッツ関数の部分集合である．しかしながら，この重みのクリッピングはいくつかの問題があることが知られている．

## 最適化Criticアーキテクチャの特性
> **命題.1** $\mathbb P_r,\mathbb P_g$をコンパクトな距離空間$\mathcal X$の2つの分布とする．このとき，$\max_{||f||_{L}\leq 1}\mathbb E_{y\sim\mathbb P_r}[f(y)]-\mathbb E_{x\sim\mathbb P_g}[f(x)]$の最適解である1-リプシッツ関数$f^{*}$が存在する．
> また，$\pi$を$\mathbb P_r,\mathbb P_g$の最適の組み合わせとする．ただし，$\mathbb P_r,\mathbb P_g$は以下で定義される：
> 「$W(\mathbb P_r,\mathbb P_g)=\inf_{\pi\in\Pi(\mathbb P_r,\mathbb P_g)}\mathbb E_{(x,y)\sim\pi}[||x-y||]$
> ただし$\Pi({\mathbb P_r,\mathbb P_g})$は周辺分布がそれぞれ$\mathbb P_r,\mathbb P_g$である同次分布$\pi(x,y)$の集合である．」
> このとき，以下の性質を満たす：
> $f^*$が微分可能であるとき，$\pi(x=y)=0$であり$x_t=tx+(1-t)y~~(0\leq t\leq1)$で定義される$x_t$は$\displaystyle \mathbb P_{(x,y)\sim \pi}\left[\nabla f^*(x_t)=\frac{y-x_t}{||y-x_t||}\right]=1$を満たす．

> **系.1** $f^*$は$\mathbb P_r,\mathbb P_g$のほとんど至る所で勾配のノルムが$1$である．
# 重み制約の困難性

WGANの重みのクリッピングが，最適化を難しくし，かりに最適化がうまくいったとしても病的な表面を持ってしまうことが明らかとなっている．以下にその立証を示すが，この現象は常に起こるわけではない．

重みクリッピングのほかに，L2ノルムクリッピングや，L1,L2ウェイト減衰を用いて実験を行ったところ，同様の問題が観測された．

バッチ正規化により，これらの問題はある程度緩和されるが，かなりの深層WGANモデルにおいては収束ができないといった問題が観測されている．

## 不十分な能力

重みのクリッピングを使用した$k-$リプシッツ制約の実装はCriticが非常に簡単な関数へと偏らせてしまう．系1で述べたように，最適なWGANのCriticは$\mathbb P_r,\mathbb P_g$のほとんど至る所で勾配のノルムが1である．重みのクリッピング下では，最大勾配ノルムが$k$を達成しようとするNNアーキテクチャが非常に単純な関数を学習してしまうことが観察される．

## 勾配の爆発と消失

WGANは損失関数と重みの制約の相互作用により最適化が困難であることが観測された．結果として，ハイパーパラメータであるクリッピング閾値$c$を綿密に調整しないと勾配が消失もしくは爆発してよい学習が行えなくなる．


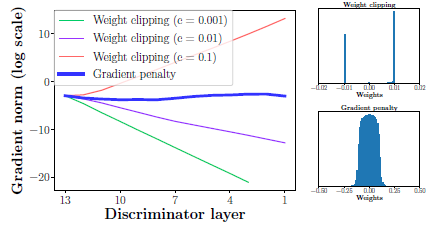
簡単なモデルにおいてこれを示すと，SwissRollデータセットに対して$c$を変えて，勾配のノルムを記録したところ，指数的に重みの爆発もしくは減衰が起きていることが判明した．なお，ジェネレータもクリティックも12層のMLPでバッチ正規化は用いていない．

# 勾配ペナルティ項

そこで，リプシッツ制約を満たすべく，重みのクリッピングではない別の方法を提示する．
微分可能な関数は任意点で1以下のノルムである勾配を持つ場合に限り，1-リプシッツであるといえる．したがって，入力に対するクリティックの出力勾配ノルムを直接制限することを検討する．
実装容易性の観点から損失関数に勾配ノルムに対する罰則項を設けて緩い制約を課すことを考える．
ランダムなサンプル$\hat{\bf x}\sim\mathbb P_{\hat{\bf x}}$に対して，新たに損失関数を以下のように定義する．

$L=\mathbb E_{\tilde{\bf x}\sim\mathbb P_g}[D(\tilde{\bf x})]-\mathbb E_{\bf x\sim\mathbb P_r}[D(\bf x)]+\lambda\mathbb E_{\hat{\bf x}\sim\mathbb P_{\hat{\bf x}}}\left[(||\nabla_{\hat{\bf x}}D\left(\hat{\bf x}\right)||_2-1)^2\right]$

## サンプリング分布

$\mathbb P_{\hat{\bf{x}}}$を，データ分布$\mathbb P_r$とジェネレータ分布$\mathbb P_g$からサンプリングされた点間を結ぶ直線に沿って暗に定義している．この方法の裏付けとしては，最適化されたクリティックが，命題1からもわかるように，$\mathbb P_r$および，$\mathbb P_g$からの結合点を接続する勾配ノルム1を有する直線を含むという事実である．任意点で単位勾配ノルムを課すことは難しいため，これらの直線上でのみ強制させている．実験的にも，この制約により十分に良い結果が得られることが分かった．

## 罰則係数

すべての実験において$\lambda = 10$としている．単純なモデルから複雑なモデルまで，様々なモデルにおいて，この値が最も良いふるまいを示したため，この値としている．

## クリティックアーキテクチャにバッチ正規化を課さない

バッチ正規化は入力バッチ全体を出力バッチへと写像する．そのため，単一の入力を単一の出力に射影するディスクリミネータの問題形式を変更してしまうといえる．バッチ全体ではなく個別入力に対してクリティックの勾配ノルムに罰則を課すため，バッチ正規化の下では，勾配罰則を科す目的がもはや有効ではなくなってしまう．バッチ正規化ではない，サンプル間の相関に従属しない正規化では，この方法においてはうまく動作し，特に，レイヤ正規化を課すことを推奨する．

レイヤ正規化: https://arxiv.org/abs/1607.06450

## 両面的罰則

勾配ノルムは1以下にさせるよりも，1に向かわせるように調整するようにさせるとよい．これは，最適なWGANでは，$\mathbb P_r$,$\mathbb P_g$下のほとんど至る所で，また，その分布間の大部分で勾配ノルムが1となるため，片面的罰則では制約が足りないであろうという経験的な推測によるものである．

# 実装
https://gist.github.com/Shirataki2/86a068ea0a3eff36974ccf9b8ab5a8cf