2023q1 Homework3 (quiz3)

contributed by <Shiritai>

測驗一

完成紅黑樹 parent 指標之指標、對齊、顏色等相關操作。

AAAA 考慮對齊，取得親代指標
指標以 long (64 bits) 對齊，由於每個地址指向一 byte (8 bits)，故真正對齊的地址需為 \(\frac{64}{8} = 8\) 的倍數，也就是最低 \(3\) 位元應為零。
不過考慮 long 在不同 ABI 下長度不一，此時可以利用 sizeof 處理跨平台的情況。
```
#define rb_parent(r) ((node_t *) ((r)->color & ~(sizeof(long) - 1)))
```
BBBB 設定顏色為紅色
單純對最低位進行標記。
```
(r)->color &= CMAP_RED; // CMAP_RED = 0
```
CCCC 設定顏色為黑色
單純對最低位進行標記。
```
(r)->color |= CMAP_BLACK; // CMAP_BLACK = 1
```

完成走訪邏輯

DDDD、EEEE 走訪左右子樹，當非走訪至葉節點且與當前節點相比較小／大時，往左／右子節點走訪。

if (res < 0) {
    if (!cur->left) {
        cur->left = node;
        rb_set_parent(node, cur);
        cmap_fix_colors(obj, node);
        break;
    }
    cur = cur->left;
} else {
    if (!cur->right) {
        cur->right = node;
        rb_set_parent(node, cur);
        cmap_fix_colors(obj, node);
        break;
    }
    cur = cur->right;
}

完成 treesort 邏輯

保存間接指標以利收尾
```
node_t **record = list;
```

將欲排序資料放入 cmap

cmap_t map = cmap_new(sizeof(long), sizeof(NULL), cmap_cmp_int);
while (*list) {
    cmap_insert(map, *list, NULL);
    list = &(*list)->next; // TODO: FFFF
}

中序遍歷整顆紅黑樹，重建 list

node_t *node = cmap_first(map), *first = node;
for (; node; node = cmap_next(node)) {
    *list = node;
    list = &(*list)->next; // TODO: GGGG
}

收尾
將 list 末個 next 設為 NULL 後，重設間接指標的起點。

*list = NULL; // TODO: HHHH
*record = first;
free(map);

圖示化分析以間接指標遍歷的邏輯

以中序遍歷重建 list，為例，其使用間接指標的技巧，避免邊界條件判斷的必要。假設從 a 走訪到 c，行為如下圖所示：

*list = node (1), list = &(*list)->next

digraph dg {
    graph[rankdir=LR]
    node [shape=record]
    first[shape=circle]
    first -> node1:c
    list[shape=circle]
    node1[label="<c> node1|<n> next ptr"]
    node2[label="<c> node2|<n> next ptr"]
    node3[label="<c> node3|<n> next ptr"]
    list -> node1:n [weight=0]
}

*list = node (2), list = &(*list)->next

digraph dg {
    graph[rankdir=LR]
    node[shape=record]
    first[shape=circle]
    first -> node1:c
    list[shape=circle]
    node1[label="<c> node1|<n> next ptr"]
    node2[label="<c> node2|<n> next ptr"]
    node3[label="<c> node3|<n> next ptr"]
    node1:n -> node2:c
    list -> node2:n [weight=0]
}

*list = node (3), list = &(*list)->next

digraph dg {
    graph[rankdir=LR]
    node [shape=record]
    first[shape=circle]
    first -> node1:c
    list[shape=circle]
    node1[label="<c> node1|<n> next ptr"]
    node2[label="<c> node2|<n> next ptr"]
    node3[label="<c> node3|<n> next ptr"]
    node1:n -> node2:c
    node2:n -> node3:c
    list -> node3:n [weight=0]
}

假設遍歷完樹，收尾時將最後一個 next 設為 NULL ~~是業界常態~~

digraph dg {
    graph[rankdir=LR]
    node [shape=record]
    first[shape=circle]
    first -> node1:c
    list[shape=circle]
    node1[label="<c> node1|<n> next ptr"]
    node2[label="<c> node2|<n> next ptr"]
    node3[label="<c> node3|<n> next ptr"]
    node1:n -> node2:c
    node2:n -> node3:c
    list -> node3:n [weight=0]
    NULL[shape=plaintext]
    node3:n -> NULL
}

測驗二

節點與平衡標記相關

取親代指標的邏輯與測驗一同理，利用 sizeof 完成跨平台的指標對齊。

static inline struct avl_node *avl_parent(struct avl_node *node)
{
    // TODO: IIII
    return (struct avl_node *) (node->parent_balance & ~(sizeof(unsigned long) - 1));
}

取顏色直接取最低兩位元即可，之所以是兩位元是因為平衡因子有 0, 1, 2 三種可能，佔 \(2\) bits。

static inline enum avl_node_balance avl_balance(const struct avl_node *node)
{
    // TODO: JJJJ
    return (enum avl_node_balance)(node->parent_balance & 3);
}

指派 `parent_balance` 成員

為其指派親代節點指標可利用之前實作的 avl_balance 函式保留平衡因子的部分：

static void avl_set_parent(struct avl_node *node, struct avl_node *parent)
{
    // TODO: KKKK
    node->parent_balance =
        (unsigned long) parent | (avl_balance(node));
}

指派平衡因子時同理可複用之前實作過的 avl_parent 函式來保留親代指標的部分：

static void avl_set_balance(struct avl_node *node,
                            enum avl_node_balance balance)
{
    // TODO: LLLL
    node->parent_balance =
        ((enum avl_node_balance) avl_parent(node)) | balance;
}

AVL 樹插入節點的平衡操作

旋轉比較難畫，就直接引用維基百科的圖了。

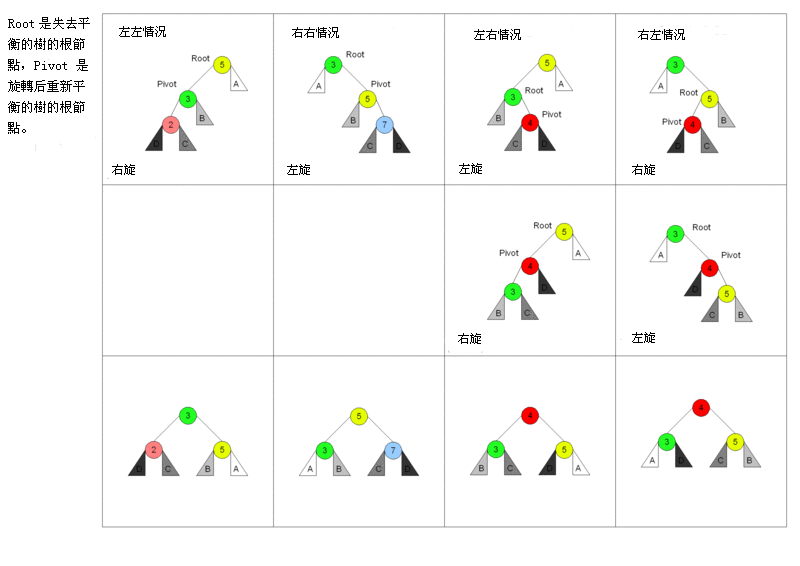
觀察 MMMM, NNNN 所在之迴圈中較前面，針對 RR／RL 所執行的左旋轉／右旋後左旋，推斷 MMMM 和 NNNN 為處理 LL／LR 的情況，故為對應的右旋轉／左旋後右旋，實作如下：

// inside while loop
if (avl_is_right_child(node)) { ... } else {
    switch (avl_balance(parent)) {
        ...
    case AVL_LEFT:
        /* compensate double left balance by rotation
         * and stop afterwards
         */
        switch (avl_balance(node)) {
        default:
        case AVL_LEFT:
        case AVL_NEUTRAL:
            // TODO: MMMM
            avl_rotate_right(node, parent, root);
            break;
        case AVL_RIGHT:
            // TODO: NNNN
            avl_rotate_leftright(node, parent, root);
            break;
        }
        ...
    }
}

測驗三

TODO

測驗四

測驗四題目

以下程式碼應實現 \(\lceil \log_2(x) \rceil\)。

int ceil_log2(uint32_t x)
{
    uint32_t r, shift;

    x--;
    r = (x > 0xFFFF) << 4;                 
    x >>= r;
    shift = (x > 0xFF) << 3;
    x >>= shift;
    r |= shift;
    shift = (x > 0xF) << 2;
    x >>= shift;
    r |= shift;
    shift = (x > 0x3) << 1;
    x >>= shift;
    return (KKKK) + 1;       
}

測驗四分析

觀察程式碼，由其行為可見當 x 大於某二的冪長度之全一時，便以 shift 蒐集某長度之全一的長度，記錄 shift 於 r 後將 x 位移 shift。從 \(16\) 個 \(1\) 開始，推測最後會處理一個 1 的情況，故我們應該看到：

// collect result of 0x3 part
// ...
r |= shift;
// collect result of 0x1 part
shift = (x > 0x1) << 0;
x >>= shift;
r |= shift;

上述程式碼對 x 的操作沒有必要，因為後續不再使用，故 (不考慮註解的) 第 3 行可去除，並可將 1, 2, 3 行簡化為：

r |= shift | x > 0x1;

至於 r 紀錄了什麼？當 x 為無號最大值 \(x_{max}\) (全一) 時，shift 一路下來捕獲了 \(16, 8, 4, 2, 1\)，並將其以 or 運算紀錄於 r，結果為 \(31\)，與 \(\lceil \log_2(x_{max}) \rceil = 32\) 差一，由此認為 return (KKKK) + 1; 的 + 1 因此出現。

這樣一來 KKKK 為何就比較明朗了。考慮前方簡化版邏輯，由於直接回傳，不需要將結果存入 r，故改為 expression 版如下：

return (r | shift | (x > 0x1)) + 1;

再來我們簡化 x > 0x1 的部分。由於我們已經使用 \(2^1, 2^1, 2^3, 2^4\) 這幾把拿來左移的尺，對於 \(32\) 位元的數字而言只可能還沒碰到原本最高的兩位，此時 x 只剩 \(0 \sim 3\) 這四種可能，故可替換其邏輯為 x >> 1，捕獲未觸碰的原最高位。

所以答案為

KKKK = r | shift | x >> 1

Syntax	Example	Reference
# Header	Header	基本排版
- Unordered List	Unordered List
1. Ordered List	Ordered List
- [ ] Todo List	Todo List
> Blockquote	Blockquote
Bold font	Bold font
Italics font	Italics font
~~Strikethrough~~	~~Strikethrough~~
19^th^	19^th
H~2~O	H₂O
++Inserted text++	Inserted text
==Marked text==	Marked text
[link text](https:// "title")	Link
![image alt](https:// "title")	Image
`Code`	`Code`	在筆記中貼入程式碼
```javascript var i = 0; ```	`var i = 0;`	在筆記中貼入程式碼
:smile:		Emoji list
{%youtube youtube_id %}	Externals
$L^aT_eX$	L^aT_eX
:::info This is a alert area. :::	This is a alert area.

2023q1 Homework3 (quiz3)

測驗一

完成紅黑樹 parent 指標之指標、對齊、顏色等相關操作。

完成走訪邏輯

完成 treesort 邏輯

圖示化分析以間接指標遍歷的邏輯

測驗二

節點與平衡標記相關

指派 parent_balance 成員

AVL 樹插入節點的平衡操作

測驗三

測驗四

測驗四題目

測驗四分析

指派 `parent_balance` 成員