###### tags: `統計` # 心理科學基礎統計 課表名稱：社會統計(二) 授課教師：陳紹慶 上課時間：每週一3:40pm ~ 5:30pm 上課教室：人社院電腦教室 --- ## 現代人需要的統計思考 上課日期：3/2 ---- ### 為什麼要學習這門課？ - 我們活在要依賴資訊才能安全生活的世界 - 例如：[國內新冠肺炎即時資訊](https://sites.google.com/cdc.gov.tw/2019ncov/taiwan?authuser=0) - 資訊：歸納的數據資料 ---- ### 如何知道資訊的可信度 - 靠自己判斷各種來源資訊的能力 - 運用工具處理要歸納的數據資料 ---- ### [podcast開放咖啡角](https://anchor.fm/opensci-cafe)的後台資訊 > 2020/2/22截圖  ---- |  |  | |---|---| ---- - 這些資訊告訴我什麼？ - 我能用這些資訊做什麼？ ---- ### 這門課要學什麼？ - 運用**統計思考**判讀與歸納資訊 - 認清**統計思考**是**科學思考**的一部分 ---- ### 這門課的學習資源 - [課程資訊公開網頁](https://www.notion.so/sauchinchen/890053e7bf0e48c6af1d19df5b500a2b) - 開源統計軟體 |[jamovi](https://www.jamovi.org/)|[JASP](https://jasp-stats.org/)| |---|---| ---- ### 個人設備調查 - 沒有自已的個人電腦？ - 自已的個人電腦無法安裝JASP與jamovi？ ---- ### jamovi下載與安裝示範影片 {%youtube QVNQh9JerjA %} ---- ### JSAP下載與安裝示範影片 {%youtube sYw8eG8hoY8 %} ---- ### 這門課的學習規劃 - 9次作業(iCan繳交) - 排程專案：[重製研究文獻統計資訊](https://hackmd.io/@CSC/Hy20fu0QL) ---- ### 補課意見收集 - 緣由：本學期第17週(6/22~6/28)有出國規劃，需要調查同學修課狀況，第三週決定補課方式。 --- ## 統計思考與研究設計 上課日期：3/9 ---- - 科學思考：<br>**假設**充分演繹事件發生原因並提出驗證原因的方法，以對原因的了解預測可能的結果；<br>**設計**驗證方法可公平發現*符合預測的正面結果*，與*不符合預測的反面結果*。 ----  [Lady tasting tea](https://en.wikipedia.org/wiki/Lady_tasting_tea)  ----  [治療性撫慰學會官網](http://therapeutictouch.org/) ----  ---- ### Emily Rosa的感應測試設計 - 假設：撫慰師的感應測試正確率應該高於隨機猜測。 - 設計：隨機製造撫慰師與施測者事前都不知道的**十次出手順序**；紀錄所有撫慰師能答對的次數。 ---- - 統計思考：</br>以科學思考形成的**假設** </br> 收集資料的**設計**符合隨機原則 </br> **分析**正面證據肯定假設對比反面證據否定假設的機率 ---- #### 資料分析展示：以Emily Rosa的感應測試資料 JASP -> Data Library -> `5. Frequencies` -> Emily Rosa \_\_\_\_\_\_\_\_\_ #### 匯出資料 Menu -> Export Data -> Save in your computer ---- ### JASP與jamovi的資料處理哲學 - 限定處理**可分析資料**，通常包含**依變項**/**應變項**及**獨變項**/**自變項** - 至少有一個可分析資料的欄位是**依變項**/**應變項** - 其他**可分析資料**欄位來自紀錄；分析者編輯新欄位；或轉換非可分析資料 ---- ### 資料編輯功能 JASP 使用系統預設試算表編輯器編輯資料；jamovi可直接編輯資料。  --- ## 測量尺度與描述統計 上課日期：3/16 ---- ### 資料尺度的設定 JASP, jamovi能自動判斷匯入資料的尺度，不一定是符合計畫的尺度。  ----  ---- ### 資料整隊(Data Wrangling) - 約佔80%的資料分析工作時間(參考[datalab視頻](https://youtu.be/B2OgFq05QMs)) - 匯入統計軟體前：資料已按欄位排列；(變項)欄位名稱已設定；**[根據自變項標記總結應變項資料](https://www.managertoday.com.tw/columns/view/54673)**。 - [匯入統計軟體後](https://scgeeker.github.io/BasicStatistics/data-manipulating.html)：過濾不需要分析的數值；轉換原始欄位；製造虛擬變項。 ---- ### 變項種類 - 展示JASP與jamovi的描述統計範例資料。 - 請指出那些欄位是**依(應)變項**，那些欄位是**獨(自)變項**。 - 如果有必要改變尺度，說明如何更改。 ---- - Fear of Statistics  ---- - Sleep  ---- - Book sales  ---- - AFL winning margins by year  ---- - 變項種類決定變項尺度 - 變項種類構成研究設計 ---- ### 統計量數 - 有資訊的統計量數：資料來自**隨機程序**。 - 能計算統計量數的變項種類：**依變項**；**隨機抽樣的自變項**。 ---- ### 什麼是隨機程序 - 個人的固定收入支出 - 打工的飲料店本月營業額 - 為了旅遊計畫準備的存款 - 某天晚上逛夜市的消費 [請作答](https://goo.gl/forms/n90a5gr2S5QJJHM52) ---- ### 數值表達的資訊 - 最有可能發現的觀察結果 - 符合收集條件的隨機資料範圍 ---- ### 統計量數的資訊 - 集中趨勢 - 變異趨勢 - 變項尺度決定表達資訊的形式 - 以gss2010為例 --- ## 統計資訊的報告 上課日期：3/11 ---- ### 呈現統計資訊的方式 - 文字 - 表格 - 圖像 - 有可以參考的建議嗎？ ---- ### 示範案例 - (**作業檢討**)專業按摩店經理的任務：一分鐘讓員工了解[當天顧客的回饋](https://docs.google.com/spreadsheets/d/1-tcb_Ff6Djk_mf-apTYUuT7V81_wT8HU9JdWn_EvmdA/edit?usp=sharing)。 - 示範檔案：[JASP](https://osf.io/a8epr/)(0.9.2),[jamovi](https://osf.io/b4kdp/) ---- ### APA 5.03(1) - 表格與圖像會不會不容易讓讀者抓到重點？ - 「今天客人的普遍反應...」 ---- ### APA 5.03(2) - 呈現載體的規格限制？ - 按規定建檔的報表 - 給股東看的簡報 - 內部會議的口頭說明 ---- ### APA 5.03(3) - 表格與圖像不是達成有效溝通的必要選項。 - 「今天上班的按摩師有三位，約三分之二的客人反應...」 ---- ### 次數分配表(Frequency Table) <small>以JASP製作</small> <small> |Feedback | Frequency | Percent | Valid Percent | Cumulative Percent | |:---:|:---:|:---:|:---:|:---:| |1 | 1 | 3.13 | 3.13 | 3.13| |2 | 3 | 9.38 | 9.38 | 12.50| |3 | 5 | 15.63 | 15.63 | 28.13| |4 | 9 | 28.13 | 28.13 | 56.25| |5 | 7 | 21.88 | 21.88 | 78.13| |6 | 5 | 15.63 | 15.63 | 93.75| |7 | 2 | 6.25 | 6.25 | 100.00 | |Missing | 0 | 0.00 |Total | 32 | 100.00 </small> ---- ### 長條圖(bar chart; bar plot) <small>以jamovi製作(JASP -> Distribution plot)</small>  ---- ### 箱形圖(boxplot)與小提琴圖(violine plot) <small>以JASP製作(jamovi必須是連續尺度)</small>  ---- ### 計算及轉換變項功能示範 - 分組變項 - 反向計分 ---- ### 圖表製作建議 ||<small>依變項為類別變項</small>|<small>依變項為連續變項</small>| |---|---|---| |<small>無獨變項</small>|<small>無分組資料：長條圖,箱形圖<br>有分組資料：次數分配表</small>|<small>無分組資料：直方圖,箱形圖/密度曲線,次數分配表<br>有分組資料：柱狀圖,多組箱形圖/密度曲線,次數分配表</small>| |<small>獨變項為相依樣本*</small>|<small>列聯表,附趨勢線柱狀圖</small>|<small>附誤差區間折線圖</small>| |<small>獨變項為獨立樣本*</small>|<small>列聯表,附趨勢線柱狀圖</small>|<small>附誤差區間折線圖或柱狀圖</small>| \* 必為分組資料 ---- ### 依變項為類別變項;無獨變項 - <small>[Emily Rosa的TT試驗](https://osf.io/rax3g/)，以所有受測者的回答次數分析</small>  ---- ### 依變項為連續變項;無獨變項 - <small>[Emily Rosa的TT試驗](https://osf.io/4k7nc/)，以每位受測者的正確率分析</small> |  |  | |---|---| ---- ### 依變項為類別變項;獨變項為相依樣本 - <small>[AGPP政黨形象廣告試片調查](https://osf.io/q6epv/)</small> ||試片前表示認同|試片前表示不認同|總數| |:---:|:---:|:---:|:---:| |試片後表示認同|5|**5**|10 |試片後表示不認同|**25**|65|90 |總數|30|70|100 ---- ### 依變項為連續變項;獨變項為相依樣本 - <small>[失智症者出現危險行為的紀錄](https://osf.io/35nk8/)</small>  ---- ### 依變項為類別變項;獨變項為獨立樣本 - <small>[線上問卷抽獎提示研究](https://osf.io/6rqvd/)</small>  ---- ### 依變項為連續變項;獨變項為獨立樣本 - <small>[身體動作與新奇感受的認知研究](https://osf.io/spn64/)</small>  ---- ### 呈現統計資訊的綜合建議 - 先了解呈現統計資訊的用途與場合，以讀者的角度思考如何有效理解。 ---- ### 呈現統計資訊的綜合建議 - 統計分析是作者檢驗問題的步驟之一，呈現統計資訊如同解釋如何推論。 ---- ### 呈現統計資訊的綜合建議 - 用一句話或一段文字就能讓讀者理解最重要的統計資訊，文字是首選。 --- ## 第一次階段考核檢討 上課日期：3/18 ---- - [JASP 示範檔案0.9.0](https://osf.io/v7r8f/) - [JASP 示範檔案0.9.2](https://osf.io/gta2p/) - [jamovi 示範檔案](https://osf.io/qtaev/) ---- ### 變項換算 - 以BMI值的計算為例 - [BMI維基百科條目](https://zh.wikipedia.org/wiki/%E8%BA%AB%E9%AB%98%E9%AB%94%E9%87%8D%E6%8C%87%E6%95%B8) ---- ### index 的分組與BMI的差異一致? - 百分位數的設定 - 次數分配表的功能 - 散佈圖的功能 ---- ### BMI分組分析 - 平均值與標準差 - 箱形圖與小提琴圖 - 極端值 ---- ### 重要資訊解讀 - BMI值的index分組差異 - BMI級別與身高體重比值的對應關係 - 性別差異的可能原因 ---- ### 風險評估的應用 - BMI級別修正 - 潛在族群差異分析 - 分層抽樣 ---- ### 實證資料的不確定性 - 描述統計(文字與圖表)必須呈現集中與變異資訊 - 事件發生的可觀察紀錄有其侷限(可觀察的對象、紀錄方法) - 有可驗證的假設，正反證據皆存在樣本偏差(bias) ---- ### 研究設計的隨機化措施 - 隨機取樣(Random Sampling):取樣對象就是測量紀錄；取樣對象涵蓋各種事件發生的可能性。 - 隨機分派(Random Assignment):有預先準備的處置；收集各種處置的測量紀錄；測量對象被分派到各種處置的機率符合預先設定的機率分佈。 - 任何隨機化措施，必須設定正反證據出現的機率分佈，才能評估證據的有效性。 --- ## 機率論：機率的計算 上課日期：3/25 ---- ### 集合論 - 根據規則，定義某個事件出現為$A_1$，其他事件出現為$A_2$，$A_3$，依此類推 - 符合條件B的事件有$A_1,A_2,A_3$ - 符合條件C的事件有$A_3,A_4,A_5$ ---- ### 集合論 - 聯集 $B \cup C = \{A_1,A_2,A_3,A_4,A_5\}$ - 交集 $B \cap C = \{A_3\}$ - 補集 $\bar{B} = \{A_4,A_5\}$ - $\bar{B} \cap \bar{C} = ?$ ---- ### 機率事件 - $A_1,A_2, ..., A_n$ 任一事件出現機率都相等，可知$P(A_x) = 1/n, x = \{1,2, ... n\}$ - $P(B) = P(A_1) + P(A_2) + P(A_3) = 3/n$ - $P(B \cup C) = ?$ - $P(\bar{B}) = ?$ - $P(\bar{B} \cap \bar{C}) = ?$ ---- ### 機率事件的排列組合 - 事件$A_x$: 投擲三枚硬幣，正面或反面朝上的組合。 |事件代號|投擲結果|發生機率| |:---:|---|:---:| |$A_1$|正、正、正|1/8| |$A_2$|反、正、正；正、反、正；正、正、反|3/8| |$A_3$|反、反、正；正、反、反；反、正、反|3/8| |$A_4$|反、反、反|1/8| ---- ### 機率事件的排列組合 - 部分結果: $C^n_x = \frac{n!}{(n-x)!x!}$ - 所有結果: $\sum_{x=0}^n C^n_x$ n: 所有可能發生的結果, x: 符合部分條件的可能發生結果 ---- ### 樣本空間 - $S_1$:至少一枚硬幣正面朝上 - $P(S_1) = P(A_1) + P(A_2) + P(A_3)$ - $S_2$:至少三枚硬幣反面朝上 - $P(S_2) = P(A_4)$ - $S_3$:沒有硬幣正面朝上 - $P(S_3) = P(A_4)$ - $S_4$:至少一枚硬幣反面朝上 - $P(S_4) = P(A_1) + P(A_2) + P(A_3) + P(A_4)$ - 以上那些機率事件總和為1？ ---- ### 條件機率 - 蒙提霍爾問題  - [請先猜猜看...](https://forms.gle/BGHFxDHbNNgEQZSV9)需要登入慈大google帳號 ---- ### 條件機率 - 來賓該不該換門? - $\theta$: 來賓一開始選擇的門; $P(\theta)$: 選擇其中一道門的機率 - $D$: 主持人打開的門; $P(D)$: 主持人打開其中一道門的機率 - $P(\frac{\theta}{D})$: 主持人打開其中一道門，來賓決定不換門而得到車子的機率 - $P(\frac{\bar{\theta} }{D})$: 主持人打開其中一道門，來賓決定不換門而未得到車子的機率 - $P(\frac{\theta}{D}) + P(\frac{\bar{\theta} }{D}) = 1$ ---- ### 貝氏定理 $P(\frac{\theta}{D}) = \frac{P(\frac{D}{\theta}) \times P(\theta)}{P(D)}$ ---- ### $P(\theta)$ 來賓選擇任何一道門的機率 = 1/n; n:節目設定的門數 ---- ### $P(D)$ 主持人打開其餘任何一道門的機率 = 1/(n-1) ---- ### $P(\frac{D}{\theta})$ - $P(\frac{D}{\theta}) = \frac{P(D \cap \theta)}{P(\theta)}$ - 若來賓選門，主持人開車是彼此獨立的事件 - $P(D \cap \theta) = P(D)P(\theta)$ - 因為來賓的選擇會影響主持人的行動，蒙提霍爾的節目不符合$\theta$與$D$彼此獨立的條件 ---- ### $\theta$ = 1號門 |狀況|*1號門*|2號門|3號門| |:---:|:---:|:---:|:---:| |選擇正確($\theta$)|車|羊|羊| |選擇錯誤($\bar{\theta}$)|羊|車|羊| |選擇錯誤($\bar{\theta}$)|羊|羊|車| ---- ### $\theta$ = 2號門 |狀況|1號門|*2號門*|3號門| |:---:|:---:|:---:|:---:| |選擇錯誤($\bar{\theta}$)|車|羊|羊| |選擇正確($\theta$)|羊|車|羊| |選擇錯誤($\bar{\theta}$)|羊|羊|車| ---- ### $\theta$ = 3號門 |狀況|1號門|2號門|*3號門*| |:---:|:---:|:---:|:---:| |選擇錯誤($\bar{\theta}$)|車|羊|羊| |選擇錯誤($\bar{\theta}$)|羊|車|羊| |選擇正確($\theta$)|羊|羊|車| ---- ### $P(\frac{D}{\theta})$是多少? $P(\frac{D}{\theta}) = P(\frac{D=?}{\theta=1}) + P(\frac{D=?}{\theta=2}) + P(\frac{D=?}{\theta=3})$ ---- ### 回首貝氏定理 $取得的資料支持假設的機率 = \frac{假設成立並取得支持資料的機率 \times 假設成立的機率}{取得資料的機率}$ ---- ### 現代統計的機率基礎 - 次數主義統計(frequentist statistics): $P(\frac{D}{\theta})$ - 貝氏統計(Bayesian statistics): $P(\frac{\theta}{D}); \frac{P(\frac{D}{\theta_1})}{P(\frac{D}{\theta_2})}$ ---- ### 更多關於貝氏定理... [林澤民：會算「貝氏定理」的人生是彩色的！該如何利用它讓生活更美好呢？](https://pansci.asia/archives/155071) [【余博講物理】貝氏定理與Monty Hall Problem](https://youtu.be/176RDyzlJck) ---- ### 隨機變數 - 間斷隨機變數 - 樂透彩號碼, 李克特量表 - 連續隨機變數 - 身高, 體重, 反應時間 - 任何隨機變數必有**值域**。 - 統計尺度規範源於隨機變數的數學定理。 ---- ### 機率分佈：函數 - 隨機變數(x)值域內任何數值，均有對應的出現機率(p)。 - 機率函數p(x)用來計算間斷隨機變數的機率法則。 - 機率密度函數**pdf**用來計算連續隨機變數的機率法則。 - 箱形圖、小提琴圖的製作基礎。 ---- ### 機率分佈：累積機率 - 對隨機變數(x)值域內任意實數，累積機率函數**cdf**用來計算實數範圍之內的累加機率。 - 計算**百分位數**的數學原理。 - 間斷隨機變數範例：[二項分佈](https://osf.io/t5rs3/) - 連續隨機變數範例：[常態分佈](https://osf.io/jzpmy/) ---- ### 隨機變數的期望值 - $E[X]$ = 隨機變數(x)值域內所有實數與對應機率的乘積和 - $E[X^2]$ = 隨機變數(x)值域內所有實數之平方與對應機率的乘積和 - 平均數 $\mu_x = E[X]$ - 變異數 $\sigma_x^2 = E[X^2] - \mu_x^2$ ---- ### 小結 - 機率的計算原理來自集合論。 - 機率事件是理想的樣本集合，各種機率分佈的計算元素。 - 兩種機率事件的發生先後構成條件機率，無法直接計算的條件機率可運用貝氏定理計算。 - 隨機變數是隨機化測量的數學基礎，構成的機率分佈是計算統計量數與統計圖表製作基礎。 --- ## 機率論：機率的模擬 上課日期：4/1 ---- ### 模擬條件機率：蒙提蒙爾問題 [蒙提蒙爾模擬器](https://osf.io/j5evz/):一萬集都決定換門而得到車子的結局次數  ---- ### 模擬條件機率：蒙提蒙爾問題 > $$ p(\frac{\bar{\theta}}{D}) = \frac{換門得到車子的模擬次數}{總模擬次數} $$ > $$ p(\frac{\theta}{D}) = \frac{換門未得到車子的模擬次數}{總模擬次數} $$  ---- ### 樂透彩中獎機率分析  ---- ### 樂透彩中獎機率分析  取自[台灣彩卷官網](http://www.taiwanlottery.com.tw/Lotto649/index.asp) ---- ### 每一期各獎項都會有人得獎嗎？ ---- ### 樂透彩中獎機率分析 - 不計有特別號的獎項，隨機變數(x)表示４個獎項的中獎號碼數:{3,4,5,6} - 各獎項中獎機率函數 > $$p(x) = \frac{C_x^6 \times C_{6-x}^{49-6}}{C_6^{49}}$$ ---- ### 樂透彩中獎機率分析  ---- ### 模擬連續十期的中獎狀況 - 請先下載[樂透彩模擬器](https://osf.io/wr8h2/)  ---- ### 樂透彩模擬器設定 - 隨機變數值域(x)及機率( p ) | x | p | |:---:|:---:| |3|0.0176504| |4|0.0009686| |5|0.0000184| |6|0.0000001| ---- ### 模擬連續S期的中獎狀況 - 更改第12行(模擬次數)與第19行(一期投注數量)的數值，重覆測試到至少一期出現首獎。　 - 模擬次數 = 樣本數。 - 投注數量 = 樣本的觀察值個數。 ---- ### 母群體 vs. 樣本 - 一次需要多少投注數量才容易出現首獎? - 至少要進行多少次模擬才容易出現首獎? - 如何調整模擬次數與投注數量，才能讓樣本估計的機率值逼近模擬器設定的機率? ---- ### 模擬器製造原理 - 大數法則(Law of large number)：固定條件的實驗重複越多次，累積結果的統計值越逼近**母群體**的**參數**(parameter, 隨機變數的值域)。 - 任何隨機程序的**母群體**，都是一套機率函數$P(\theta)$。 > 隨機變數涵括所有可能結果，以及給定各隨機變數發生機率之函數。 ---- ### 模擬器製造原理 - 每一次模擬結果，就是一組樣本，可總計一筆**母群體參數**的估計值，也就是**期望值**。 - 模擬多次累積的樣本，形成**期望值**的**抽樣分佈(Sampling Distribution)**。 - 抽樣分佈逼近符合資料隨機性質的條件機率$P(\frac{D}{\theta})$；$P(\frac{D}{\theta})$不一定等於$P(\theta)$。 ---- ### 二項分佈 - 下載[二項分佈示範檔案](https://osf.io/t5rs3/)  ---- ### 二項分佈：理論的機率函數 隨機變數 $X \sim B(n, p)$ ||| |---|---| ---- ### 二項分佈：母群體是伯努利事件的抽樣分佈 |母群體(n = 2; p = 0.5)|抽樣分佈(N = 10)| |:---:|:---:| ||| ---- ### 常態分佈 - 下載[常態分佈示範檔案](https://osf.io/jzpmy/)  ---- ### 常態分佈：理論的機率函數 隨機變數 $X \sim N(0, 1)$ ||| |---|---| ---- ### 常態分佈：母群體是均勻分佈的抽樣分佈 |母群體(均勻分佈 -4 ~ 4)|抽樣分佈(N=10)| |:---:|:---:| ||| --- ## 機率論小結 上課日期: 4/8 ---- [Seeing theory](https://seeing-theory.brown.edu)<br> **統計理論視覺化** ---- ### 名詞對照:章節標題 |繁中|簡中| |:---:|:---:| |基礎機率論|基础概率论| |進階機率論|进阶概率论| |機率分佈|概率分布| |推論統計：次數主義學派|统计推断：频率学派| |推論統計：貝氏學派|统计推断：贝叶斯学派| |回歸分析|回归分析| ---- ### 名詞對照:基礎機率論 |繁中|簡中| |:---:|:---:| |機率事件|概率事件| |機率分佈|*重量分布*| |期望值<br>[模擬作業](https://forms.gle/e2z9LH9mvfQuJnPC7)|期望| |變異數<br>[模擬作業](https://forms.gle/uhqqfBnL4ephwibY9)|方差| |隨機變數|随机变量| ---- ### 名詞對照:進階機率論 |繁中|簡中| |:---:|:---:| |古典機率|古典概型| |條件機率|条件概率| [蒙提霍爾問題似然性示意圖上傳表單](https://forms.gle/8dA2PuCH8yZbgNex5) ---- ### 名詞對照:機率分佈 |繁中|簡中| |:---:|:---:| |隨機變數|随机变量| |常態分佈|正态分布| |中央極限定理|中心极限定理| ---- ### [二項分佈jamovi](https://osf.io/t5rs3/)使用訣竅 - 伯努利分佈：更新第7行`p <-`之後的數值 - 二項分佈：更新第17行`N <-`與第32行`P <-`之後的數值 - [查表對照](http://eschool.kuas.edu.tw/tsungo/Publish/Appendix.pdf) ---- ### [常態分佈jamovi](https://osf.io/jzpmy/)使用訣竅 - 常態分佈：更新第24行`M <-`與第25行`SD <-`之後的數值 - [查表對照](http://eschool.kuas.edu.tw/tsungo/Publish/Appendix.pdf) --- ## 次數主義推論統計 上課日期: 4/15 ---- ### [中央極限定理](https://seeing-theory.brown.edu/probability-distributions/cn.html#section3) 回家作業檢討與反思 ---- ### 反覆抽樣與中央極限定理 - 無法掌握母群體期望值，抽樣分佈會是什麼樣？ - 現實案例：[觀測黑洞](https://thestandnews.com/cosmos/%E9%BB%91%E6%B4%9E%E7%85%A7%E7%89%87%E7%84%A1%E5%90%8D%E8%8B%B1%E9%9B%84-katie-bouman/?fbclid=IwAR0z749sUVziD50-r-BeFZvyp_z-3QgHLsDVbLyV4cy7bSur0Xb66u6rtqE) [BootStrap Method](https://seeing-theory.brown.edu/frequentist-inference/cn.html#section3) [回家作業#06反覆抽樣版](https://osf.io/g4jqh/) ---- ### 再談tea lady ||| |---|---| ---- ### 二項檢定 [jamovi示範檔](https://osf.io/9ftwe/) [JASP0.9.0.1示範檔](https://osf.io/h7bm6/) ---- ### 解讀tea lady的測試結果 |<small>假設</small>|<small>結果</small>| |---|---| |只是亂猜|| |十次中九|| ---- ### p值之父表示... - p值是**觀察結果與期望值的差別程度** - $p\ value = P(X > T(x_a)|\theta_a)$ - $\theta_a$:預期結果的期望值; $T(x_a)$: 根據觀察結果對期望值的估計 ---- ### p值的計算方法 1. 運用**符合**抽樣分佈的機率函數 2. 運用**逼近**抽樣分佈的機率函數 ---- ### 信賴區間(confidence interval) - 採用Clopper & Pearson(1934)提出的[估計方法](https://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval#Clopper%E2%80%93Pearson_interval)。 - JASP提供視覺化選項。 ---- ### 測試報告 - <small>第一次聚會：四組都答對。根據亂猜的答對率(0.5)，這次答對率(100%)之*p*值為.125，95% C.I.[0.389,1.000]包含0.5；根據有能力十次中九的答對率(0.9)，這次答對率(100%)之*p*值為1.0，95% C.I.[0.389,1.000]包含0.9。</small> - <small>第二次聚會：六組都答對。根據亂猜的答對率(0.5)，這次答對率(100%)之*p*值為.031，95% C.I.[0.541,1.000]未包合0.5；根據有能力十次中九的答對率(0.9)，這次答對率(100%)之*p*值為1.0，95% C.I.[0.541,1.000]包含0.9。</small> - <small>第三次聚會：十組答對九組。根據亂猜的答對率(0.5)，這次答對率(90%)之*p*值為.021，95% C.I.[0.555,.997]未包合0.5；根據有能力十次中九的答對率(0.9)，這次答對率(90%)之*p*值為1.0，95% C.I.[0.555,.997]包含0.9。</small> ---- ### 測試結論 - 一場要測試的組數越多，這位女士的答對率與亂猜的答對率(0.5)相差越大，95%信賴區間越不相容亂猜的答對率；每場答對率與有能力十次中九的答對率無明顯差別，95%信賴區間與十次中九的機率值保持相容。三場表現支持這位女士有能力分辨奶茶的沖煮方式。 --- ## 第二次階段考核檢討 上課日期：4/22 ---- ### JASP參考分析 - [0.9.0](https://osf.io/vnyg8/) - [0.9.2](https://osf.io/zde6q/) ---- ### 每位TT的答對率是0.5 - 根據亂猜的答對率(0.5)，所有受測TT的答對率之*p*值最小值為0.344，最大值為1；答錯率之*p*值最小值為0.344，最大值為1。每位受測TT的95% C.I.都包含0.5。 ---- ### 設定訓練有素的TT答對率是0.9 - 根據設定的答對率(0.9)，答對率最高的第六位TT(答對率0.7)之*p*值最大(.07)，95% C.I.[0.348 0.933]包含答對率0.9。其他14位TT的答對率之*p*值都小於.07，95% C.I.都沒有包含0.9。 - 答錯率最高的三位TT(答錯率0.7)之*p*值最大(.07)，95% C.I.[0.348 0.933]包含答錯率0.9。 ---- ### 分析結論 - 除了第六位TT的答對率(0.7)與設定有本事的答對率(0.9)之差別最小，未達到.05的判斷門檻/信賴區間相容0.9；14位TT的答對率與0.9的差別更大，皆有超過.05的判斷門檻/信賴區間不相容0.9。所有TT的答對率與隨機亂猜的答對率(0.5)之差異分析，無法確認有明顯差別/信賴區間相容0.5。以這次15位TT的測試結果來說，無法證實有能力的TT們發揮他們宣稱的能力。 ---- ### TT們真有本事？ - TT們測試時的狀況不佳？ - Emily Rosa設計的測試方法不夠嚴謹？ ---- ### [再一次理解統計思考](https://scgeeker.github.io/BasicStatistics/intro.html#intro_stat) - 可測試的假設 - 可實作的測試方法 - 正反證據的成立條件 ---- ### 認識p值的估計方法 - 下載[完整版二項檢定](https://osf.io/ubqs5/) - 以精確的二項分佈估計(distrACTION) - 以模擬的抽樣分佈估計(Rj Editor) ---- ### 解析型一與型二錯誤率  ---- ### 什麼因素會影響型一與型二錯誤率 - 改變以下數值，觀察估計的變化 - 全部反應數目 - H1答對率 - 真陰率(True Negative Rate) ---- ### 不是回家作業 - [培養本土嗅癌犬的生技公司資訊](http://www.sharp-biotech.com.tw/index.html#about) - 你能否辨認首頁提供的兩個統計資訊：**準確率**與**偽陽性**，分別代表今天上課提的那兩種機率？ --- ## 單一樣本的推論統計 上課日期: 4/29<br> [心理科學基礎統計 單元5](https://scgeeker.github.io/BasicStatistics/onesample.html) ---- - 奠基於抽樣分佈的虛無及對立假設 - 結論犯錯的機率：型一與型二錯誤率 - p值的來源 - 母數與無母數統計 ---- ### TT測試結果的隨機變數 <section> <div style="text-align: left; float: left;"> <p data-markdown>- H0隨機變數</p> |x|p| |---|---| |0|0.5| |1|0.5| </div> <div style="text-align: right; float: right;"> <p data-markdown>- H1隨機變數？</p> |x|p| |---|---| |0|0.2| |1|0.8| </div> </section> ---- ### TT測試結果的虛無/對立假設 ||| |---|---| ---- ### TT測試結果的錯誤率估計 ||二項檢定|t檢定| |---|---:|---:| |型一|4.28 %|2.75 %| |型二|0 %|0.6 %| ---- ### TT測試結果的p值 |二項檢定|t檢定(雙側)| |---|---| ||| ---- ### 兩種機率計算 - p值：使用逼近抽樣分佈的機率函數計算累積機率 - 型一/型二錯誤率：模擬上萬次的實驗結果，因超過標準而誤判的次數比例 ---- ### TT測試結果的信賴區間 - 抽樣分佈的每一次實驗結果都是期望值的估計 - [seeing theory圖解](https://seeing-theory.brown.edu/frequentist-inference/cn.html) - 選項設定：student t; n = 15; 1 - $\alpha$ = .95 ---- ### p值 vs. 信賴區間 - 計算 vs. 模擬 ---- ### 母數 vs. 無母數 - 能否掌握研究假設的期望值？ - 各種期望值的抽樣分佈是否遵循中央極限定理成型？ ---- ### [預先註冊](https://scgeeker.github.io/BasicStatistics/onesample.html#onesample-preregistration) - 收集或分析資料之前，研究者自我約定... - 收集的資料數量 <- 樣本數估計 - 有效資料的條件 <- 正誤反應;未作答... - 分析資料的方法 <- 描述統計圖表;推論統計 - 分析結果的判讀原則 ---- ### 作業#07檢討 - 事先自訂判斷水準 - 判斷水準來自分析者對問題的洞見 - 為何心理科學少見單一樣本分析? --- ## 相依樣本假設檢定 上課日期: 5/6 [相依樣本的推論統計](https://scgeeker.github.io/BasicStatistics/paired.html) ---- ### 母數檢定範例 - 失智症患者[在有月亮的日子，出現破壞行為的次數，比沒有月亮的日子多嗎](https://scgeeker.github.io/BasicStatistics/paired.html#paired-continuous-case)？  ---- ### 運用相依樣本t檢定的基本條件 - [jamovi示範檔案](https://osf.io/pfmkz/) - 對應研究假設的抽樣分佈是什麼樣子？ - 為何t分佈較符合抽樣分佈？ - 型一與型二錯誤率該如何取捨？ - 信賴區間的意義？ ---- ### 雙尾檢定示範 |[jamovi](https://osf.io/pfmkz/)|| |---|---| |[JASP](https://osf.io/35nk8/)|| ---- ### 單尾檢定示範 |[jamovi](https://osf.io/pfmkz/)|| |---|---| |[JASP](https://osf.io/35nk8/)|| ---- ### 報告規範 - [寫作範例](https://scgeeker.github.io/BasicStatistics/paired.html#paired-continuous-t) ---- ### 效果量、考驗力、樣本數 - 研究任務是測量差異，效果量是估計最小樣本數的重要指標 - 已知能測得的效果量：根據建議考驗力確認最小樣本數 - 未知能測得的效果量： - 比較兩項平均值差異：運用 - 多組比較/多因子設子：設定數據模擬可能效果量的最小樣本數 ---- ### 預先註冊的樣本數估計  ---- ### 無母數檢定範例 ||| |---|---| ---- ### 政黨廣告試映調查  </br> from Navarro and Foxcroft (2018) unit 10.7 </br> [jamovi示範檔案](https://osf.io/q6epv/) ---- ### 運用McNemar檢定的基本條件 || |---| |$$ 統計值 = \frac{(b - c)^2}{b + c} $$| ---- ### 運用McNemar檢定的基本條件 - 如果b與c的總和不超過20，樣本機率函數符合二項分佈 - 如果b與c的總和超過20，樣本機率函數符合**自由度為1**的[卡方機率分佈](https://seeing-theory.brown.edu/probability-distributions/cn.html#section2) ---- ### jamovi檢定示範  ---- ### McNamer檢定的型一與型二錯誤率  ---- ### McNamer檢定的型一與型二錯誤率 ||30|50| |---|---|---| |Type 1 error|~ 0.005|| |Type 2 error|~ 0.10|| ---- ### 報告規範 - [寫作範例](https://scgeeker.github.io/BasicStatistics/paired.html#paired-categorical-McNemar) --- ## 獨立樣本假設檢定 上課日期: 5/13;5/20 [獨立樣本的推論統計](https://scgeeker.github.io/BasicStatistics/independent.html) ---- ### 獨立樣本的無母數統計 - 適用時機：比較各組次數差異 - 常用方式：一因子適合度檢定；二因子獨立性/關聯性檢定 ---- ### 適合度檢定範例介紹 - 某位推理小說家寫作最新作品的過程，同時開網路直播說故事，邀請觀眾在最後一回之前，猜猜真正兇手是五名角色A，B，C，D，E之中那一名？根據情節設計，他預想最多觀眾會猜角色A，然而真兇其實是角色E。直播最後一回之前，他公佈每位角色的觀眾投票人數，統計結果下表： ---- ### 「誰是真兇」投票結果 - [jamovi示範檔案](https://osf.io/kcswx/) - [JASP示範檔案](https://osf.io/9sdbv/) |A|B|C|D|E| |:---:|:---:|:---:|:---:|:---:| |58|41|41|42|18| ---- ### 「誰是真兇」分析任務 - 小說家的情節設計成功誤導讀者的推論了嗎？ ---- ### 適合度檢定基本條件 - 唯一獨變項，且為類別變項 - 依變項是各類別**觀察次數**，可根據問題目標設定**期望次數** - 類別數目決定自由度，決定抽樣分佈**樣態** - 出現總次數決定抽樣分佈**變異** ---- ### 適合度檢定的統計數 $\sum\frac{(觀察次數 - 期望次數)^2}{期望次數}$ - 成功：$觀察次數 \neq 期望次數$ - 失敗：觀察次數 = 期望次數 ---- ### 適合度檢定的抽樣分佈 |成功|$n_A \neq n_B \neq n_C \neq n_D \neq n_E$| |---|---| |失敗|$n_A = n_B = n_C = n_D = n_E$| - 為何上述設定適用小說家的問題？ ---- ### 適合度檢定的抽樣分佈  ---- ### 適合度檢定的抽樣分佈 - 測試與觀察：調整總次數(Total)，觀察模擬結果 ||300|200|100| |---|---|---|---| |Type 1 error||~ 0.05|| |Type 2 error||~ 0.025|| ---- ### 適合度檢定的判斷水準  ---- ### 適合度檢定示範:jamovi  ---- ### 適合度檢定示範:JASP  ---- ### 適合度檢定的報告 > 根據.05的判斷水準，200位觀眾認為兇手是角色A的人數，明顯多於認為兇手是角色E的人數，卡方檢定顯示$\chi^2$(4, N=200) = 20.35, p < .001。作家可宣告情節設計成功。 ---- ### 獨立性/關聯性檢定範例介紹 Seo等人(2007)調查1,184位美國中西部大學生平常從事的運動強度(低度、溫和、劇烈)，與日常攝取水果累積量(少量、一般、超量)之間的關係。研究者認為兩種條件之間並非無關，所以分析工作一開始，使用卡方檢定確認之，再計算相關係數。示範資料已內建於JASP之`Data Library` -> `5. Frequency` -> `Health Habits`。 ---- ### 運動強度與水果攝取量關聯性分析任務 - 大學生的運動強度與水果攝取量有一定程度的關聯性嗎？ - [jamovi示範檔案](https://osf.io/j86hw/) ---- ### 獨立性/關聯性檢定使用條件 - 可組織**列聯表**(contigency table)的兩套獨變項，皆為類別變項 - 依變項是各類別**觀察次數**，可根據問題目標設定**期望次數** - 類別數目決定自由度，決定抽樣分佈**樣態** - 出現總次數決定抽樣分佈**變異**與**去中央化程度** ---- ### 解析列聯表 ||低度|溫和|劇烈|**總和**| |---|---|---|---|---| |少量|$O_{11}$|$O_{12}$|$O_{13}$|$R_1$| |一般|$O_{21}$|$O_{22}$|$O_{23}$|$R_2$| |超量|$O_{31}$|$O_{32}$|$O_{33}$|$R_3$| |**總和**|$C_1$|$C_2$|$C_3$|N| - $E_{ij} = \frac{R_i \times C_j}{N}$ - O:觀察次數; E:期望次數 ---- ### 獨立性/關聯性檢定的統計數 $\sum_i\sum_j\frac{(觀察次數_{ij} - 期望次數_{ij})^2}{期望次數_{ij}}$ ---- ### 獨立性/關聯性檢定的抽樣分佈  ---- ### 獨立性/關聯性檢定的抽樣分佈 - 測試與觀察：調整總次數(Total)，觀察模擬結果 ||1500|1184|800| |---|---|---|---| |Type 1 error, 無ncp||~ 0.30|| |Type 1 error, 有ncp||~ 0.03|| |Type 2 error, 無ncp||~ 0.006|| |Type 2 error, 有ncp||~ 0.140|| ---- ### 獨立性/關聯性檢定的判斷水準 **留意罩門！**  ---- ### 獨立性/關聯性檢定示範:jamovi  ---- ### 獨立性/關聯性檢定示範:JASP  ---- ### 獨立性/關聯性檢定的報告 > 根據.05的判斷水準，1184位大學生平常運動強度與攝食水果的總量，應該有關聯性，卡方檢定顯示$\chi^2$(4, N=1184) = 14.152, p = .007。相關係數分析也支持一致的結論，Kendall's $\tau$ = 0.061, p = .022。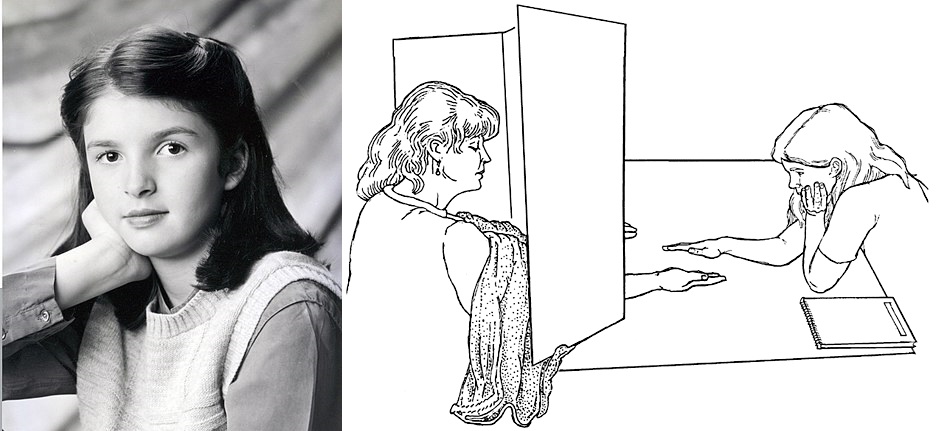 ---- ### 獨立樣本的母數統計 - 適用時機：比較兩組或多組平均數差異 - 常用方式：兩組獨立樣本t檢定;多組單因子變異數分析 ---- ### 獨立樣本範例 - 順時針轉動讓你的思想更開放？(Topolinski & Sparenberg, 2012)  ---- - Topolinski 與 Sparenberg (2012)報告**顯著**的結果。 - Wagenmakers等人(2017)招募接近原始研究的人數，採用相同的實驗方法，能否再現原始結果？ ---- ### 獨立樣本t檢定基本條件 - 獨變項是組間標記，各組採隨機分派收集參與者資料。 - 依變項對應各組期望值，比較平均值之間的差異。 - **變異等量假設**：各組資料變異數無差異。 - **常態分佈假設**：組間差異抽樣分佈符合常態分佈。 ---- ### 再現研究結果  [jamovi示範](https://osf.io/spn64/)<br> [JASP示範](https://osf.io/dkwuf/) ---- ### 模擬數據來源  ---- ### 分組模擬抽樣分佈  ---- ### 常態性檢定  ---- ### 等變異性檢定  ---- ### [獨立t檢定的策略](https://statkat.com/stattest.php?t=10&t2=9)  ---- ### 合併樣本標準差 - $s_p = \sqrt{\frac{(n_1 - 1) \times s_1^2 + (n_2 - 1) \times s_2^2}{n_1 + n_2 - 2}}$ - $se = s_p \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}$ ---- ### 組間差異的抽樣分佈  Type 1 error ~ .025 Type 2 error ~ .90 ---- ### 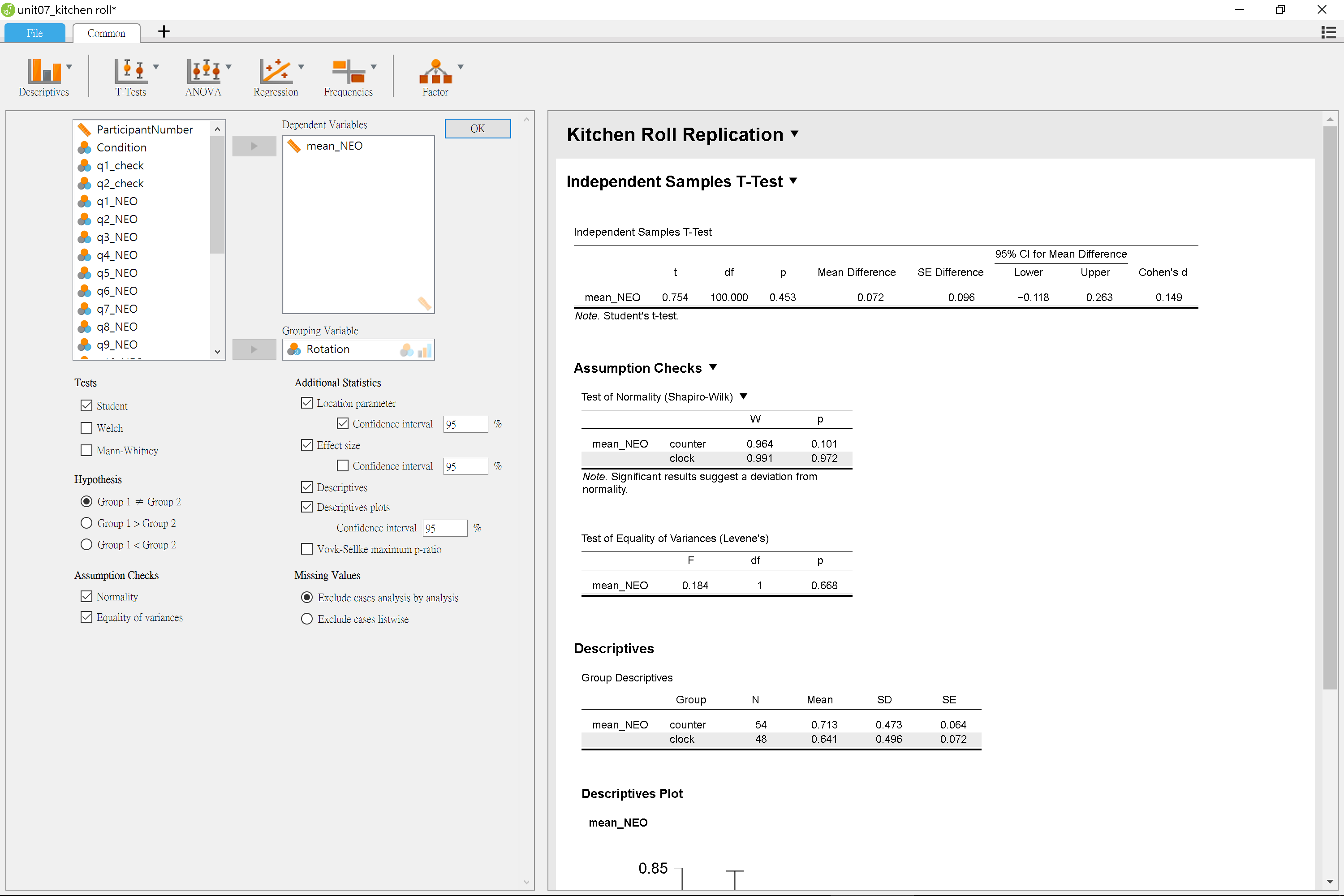獨立樣本t檢定示範: JASP  ---- ### 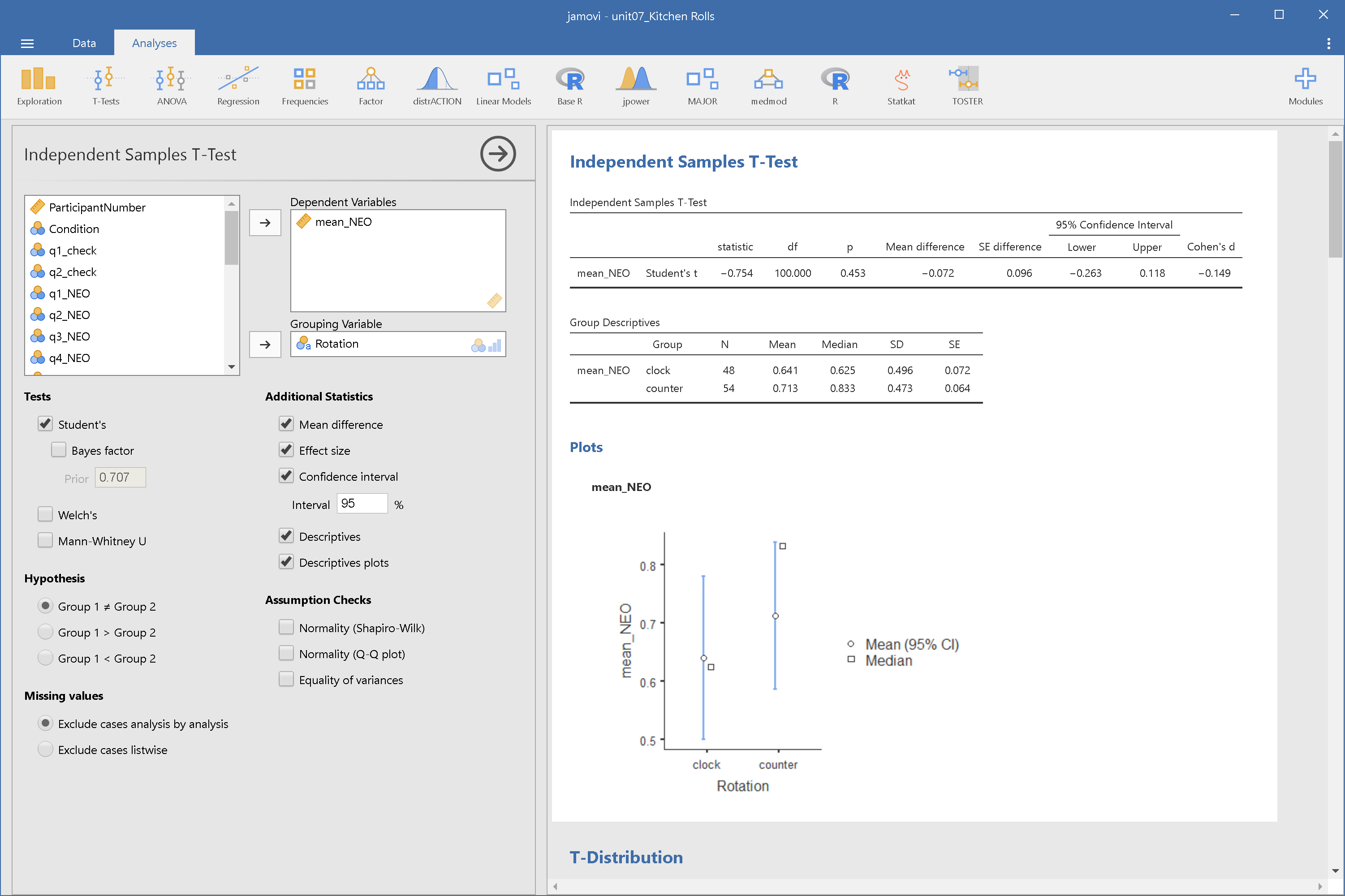獨立樣本t檢定示範: jamovi  ---- ### 獨立樣本t檢定報告 > 順時針捲動的平均評分比逆時針捲動的平均評分高0.072分(順時針：M = 0.641, SD = 0.496；無關聯：M = 0.713, SD = 0.473， 95% CI [-0.118 0.263])，並未達到事先宣告的統計顯著水準，*t*(100) = 0.754, *p* = .453, *d* = 0.149。 ---- ### 獨立樣本t檢定的效果量 - $Cohen's d = \frac{\bar{y_1} - \bar{y_2}}{s_p}$ - 限定符合變異數等量及常態性。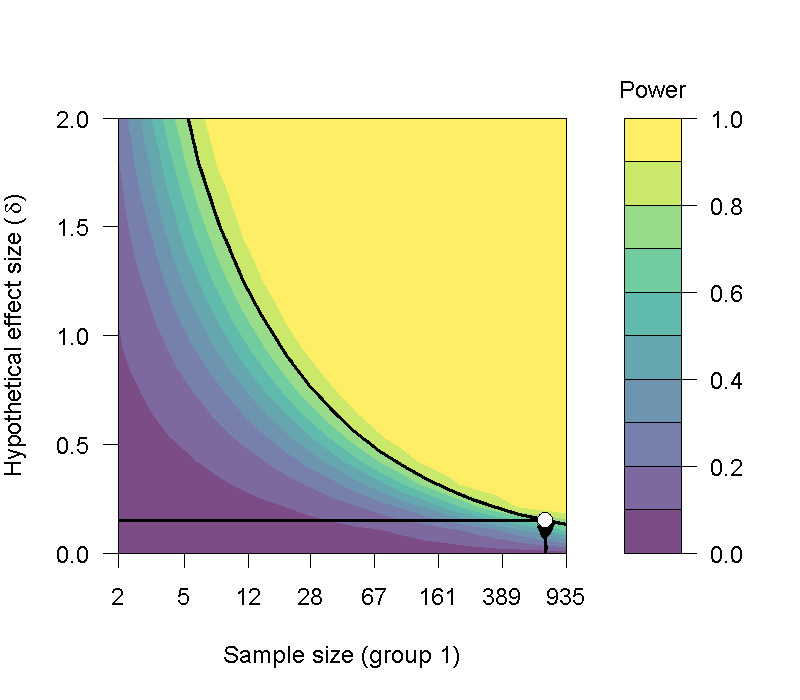 ---- ### 獨立樣本的樣本數估計  ---- ### 低效果量(0.2以下)的研究難題 - 第一次研究通常難以判斷 - 需要人數必須近千人，才能保障顯著結果的品質 - 樣本數越少，越不容易判斷導致結果的直接因素 ---- ### 探索效果量與考驗力 - 有理論預測分組測驗的差異之效果量(Cohen's d)在0.5到1.0之間，請估計以下條件達到的考驗力 |0.5|0.6|0.7|0.8|0.9|1.0| |:---:|:---:|:---:|:---:|:---:|:---:| |30|25|40|20|15|15| |雙尾$\alpha$ = .05|單尾$\alpha$ = .05|雙尾$\alpha$ = .01|單尾$\alpha$ = .01|雙尾$\alpha$ = .005|單尾$\alpha$ = .005| --- ## 相關與迴歸簡介 上課日期：5/27</br> [相關與迴歸教材](https://scgeeker.github.io/BasicStatistics/corr-reg.html) ---- ### 相關與迴歸的功能 - 相關；兩變項之間存在任何可能關係的指標 - 迴歸：歸納可由自變項預測依變項的線性關係 ---- ### 範例：[安德森鳶尾花資料庫](https://zh.wikipedia.org/wiki/%E5%AE%89%E5%BE%B7%E6%A3%AE%E9%B8%A2%E5%B0%BE%E8%8A%B1%E5%8D%89%E6%95%B0%E6%8D%AE%E9%9B%86) |山鳶尾(setosa)|變色鳶尾(vericolor)|維吉尼亞鳶尾(virginica)| |:---:|:---:|:---:| |||| ---- ### 範例：[安德森鳶尾花資料庫](https://zh.wikipedia.org/wiki/%E5%AE%89%E5%BE%B7%E6%A3%AE%E9%B8%A2%E5%B0%BE%E8%8A%B1%E5%8D%89%E6%95%B0%E6%8D%AE%E9%9B%86) - 相關：花萼和花瓣的長度與寬度，最能區辨品種的特徵 - 迴歸：運用花萼或花瓣的特徵A，估計花萼或花瓣的特徵B  ---- ### 皮爾森相關係數的使用條件 - 適用範圍：兩個變項都是連續變項 - 樣本數少於一百，應做費雪轉換，維持常態性。 ---- ### 示範案例：五大人格特質 - JASP -> Data Library -> 4. Regression -> Big Five Personality Traits  ---- ### 計算皮爾森相關係數 |母數|樣本| |:---:|:---:| ||| ---- ### 費雪轉換公式與使用時機 -  - 建議樣本數少於三十時使用。 ---- ### 費雪轉換校正非常態資料 - <small>盡責性（Conscientiousness）與情緒不穩定性（Neuroticism）之相關係數=-0.368。如果只有12位樣本資料：</small> - <small>~黑色\~原始資料模擬抽樣分佈；紅色\~原始資料費轉轉換後模擬抽樣分佈~</small>  ---- ### 費雪轉換不校正估計偏誤 - <small>盡責性（Conscientiousness）與情緒不穩定性（Neuroticism）之相關係數=-0.368。如果使用500筆樣本資料：</small> - <small>~黑色\~原始資料模擬抽樣分佈；紅色\~原始資料費轉轉換後模擬抽樣分佈~</small>  ---- ### 相關係數的意義  ---- ### 相關係數的抽樣分佈 - $H_1:r_{Conscientiousness \times Neuroticism} \neq 0$ - $H_0:r_{Conscientiousness \times Neuroticism} = 0$  ---- ### 簡單迴歸 - 自變項(X)與依變項(Y)有無限多種線性關係，皆稱為迴歸。 - 必要條件：以自變項(X)估計的依變項數值($\hat{Y}$)，與實際依變項數值(Y)之差異平方和，是所有線性關係中最小。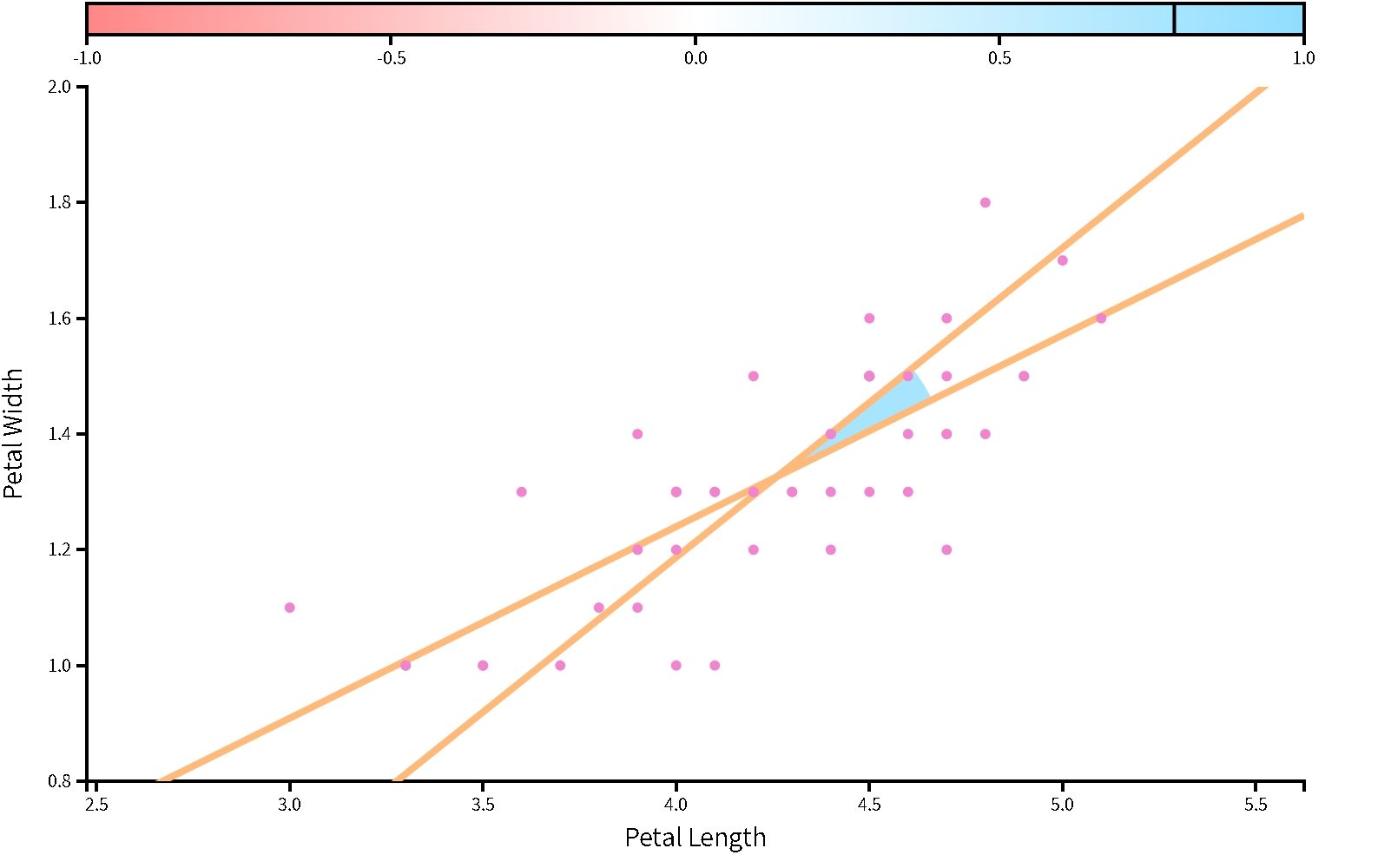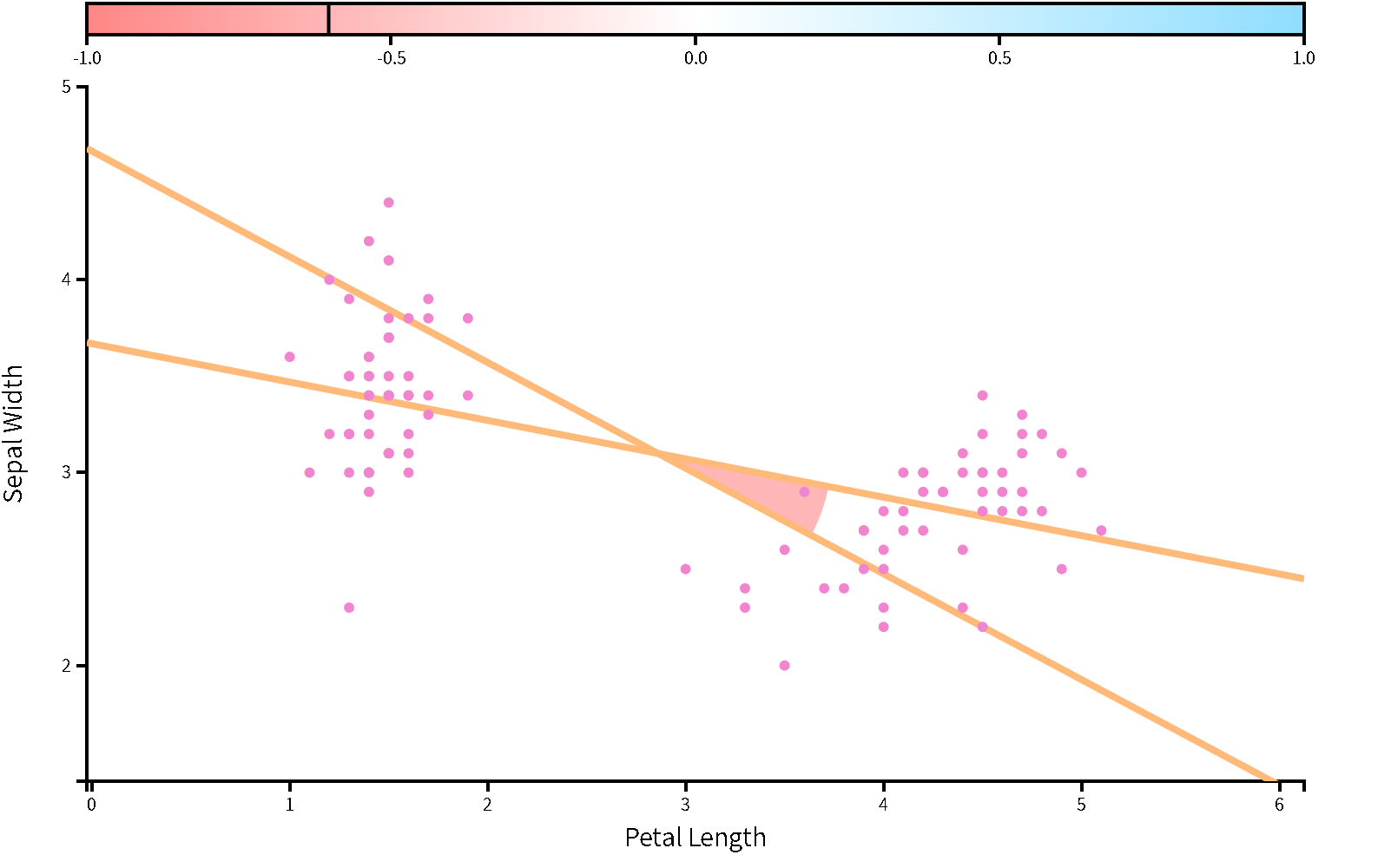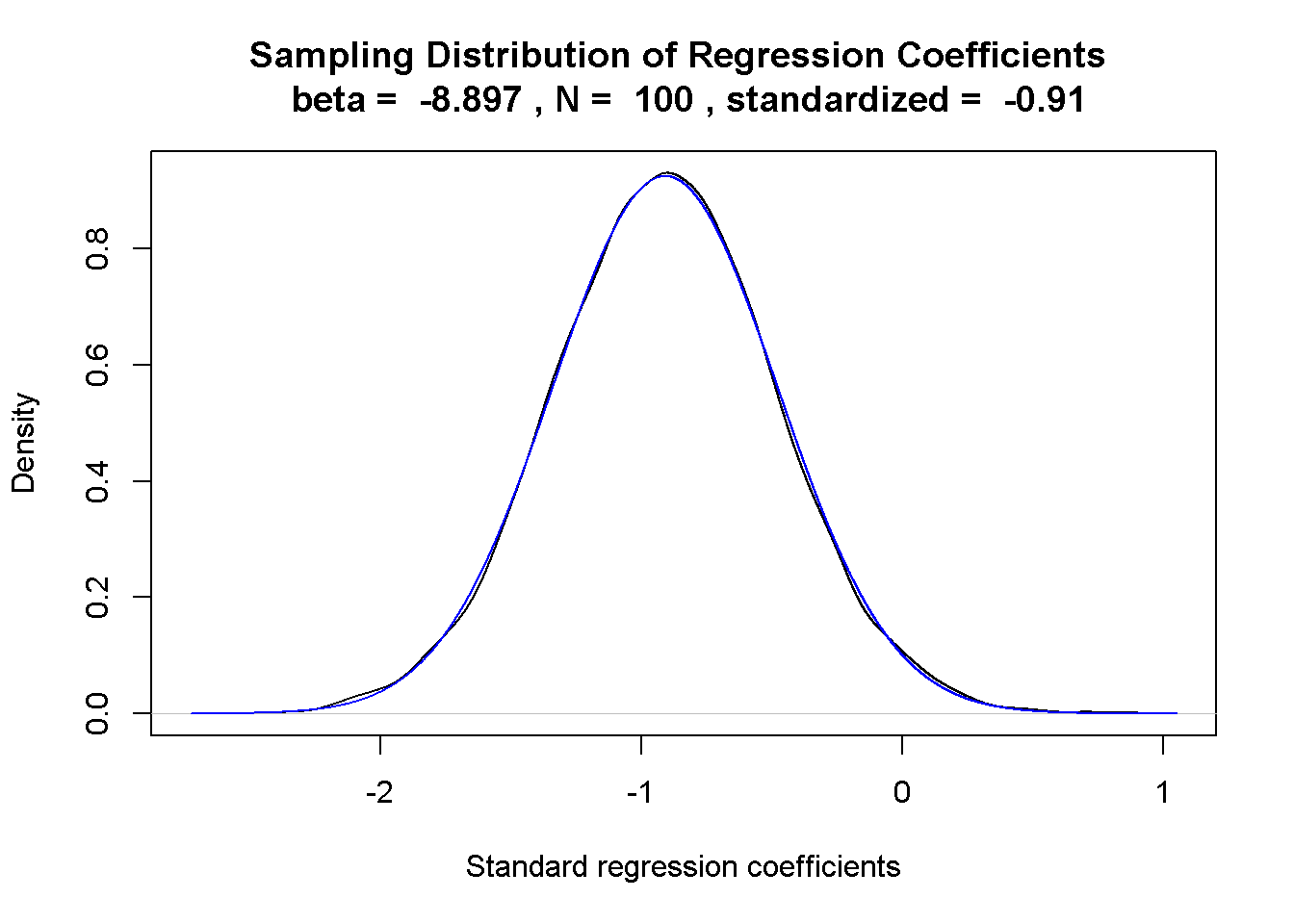 - 簡單迴歸必定通過自變項(X)與依變項(Y)的平均值；通過平均的迴歸不一定是簡單迴歸 ---- ### 相關與迴歸 |正相關|負相關| |:---:|:---:| ||| ---- ### 示範資料：新手爸爸100天育兒紀錄 - 爸爸每天自評歹命度(Y) \~ 爸爸每天睡眠時間(X) - [JASP示範檔案](https://osf.io/bmgtv/);[jamovi示範檔案](https://osf.io/g5ycu/)  ---- ### 相關係數 = 標準化迴歸係數    ---- ### 迴歸係數的抽樣分佈  ---- ### 最小平方迴歸 - $SS_{Total} = \sum\sum(Y - \bar{Y})^2$ - $SS_{Regression} = \sum\sum(\hat{Y} - \bar{Y})^2$ - $SS_{Error} = \sum\sum(Y-\hat{Y})^2$ -> 殘差平方和   ---- ### 估計標準誤與迴歸信賴區間 ||| |---|---|  --- ## 復習：以線性模型理解基礎統計 #### 上課日期：2019/6/3 [教材網頁](https://scgeeker.github.io/tests-as-linear/index.html) ---- - 簡單迴歸+多元迴歸 - 無母數統計是母數統計的序列化 - 示範檔案使用最新版JASP與jamovi ---- ||<small>相關</small>|<small>單一平均數</small>|<small>相依樣本</small>|<small>兩組獨立樣本</small>| |:---:|:---:|:---:|:---:|:---:| |<small>迴歸式</small>| $y= \beta_0 + \beta_1 x$ | $y = \beta_0$ | $y_1 - y_2 = \beta_0$ | $y= \beta_0 + \beta_1 x_i$ | |<small>虛無假設(H0)</small>| $\beta_1 = 0$ | $\beta_0 = 0$ | $\beta_0 = 0$ | $\beta_1 = 0$ | |<small>示範資料</small>| <small>[data](https://osf.io/gdshp/);[JASP](https://osf.io/efdsu/)</small> | <small>[data](https://osf.io/dkmjg/);[jamovi](https://osf.io/4sdgv/)</small> | <small>[data](https://osf.io/dvw7g/);[jamovi](https://osf.io/xdjh9/)</small> |<small>[data](https://osf.io/sja2e/);[jamovi](https://osf.io/3f6nd/)</small> | ---- ||<small>迴歸式</small>| |:---:|:---:| |<small>適合度檢定</small>| $log(y_i) = log(N) + log(\alpha_i)$ <br> <small>[data](https://osf.io/c84ep/);[jamovi](https://osf.io/2w8dm/)</small> | |<small>獨立性/關聯性檢定</small>|$log(y_i) = log(N) + log(\alpha_i) + log(\beta_i) + log(\alpha_i \beta_i)$ <br> <small>[data](https://osf.io/ep32u/);[jamovi](https://osf.io/2qtfc/)</small> | --- ## 獨立樣本變異數分析 上課日期：2019/6/10 [教材網頁](https://scgeeker.github.io/BasicStatistics/oneway-anova.html) ---- ### 廻歸 vs. 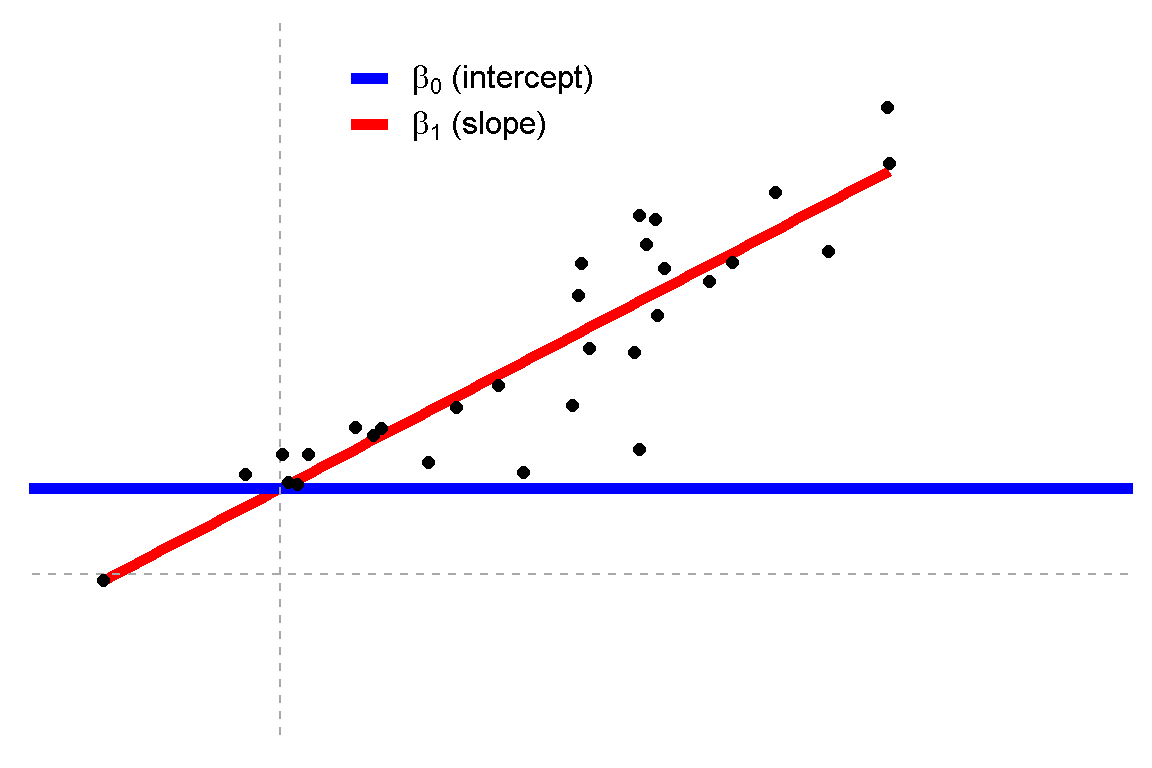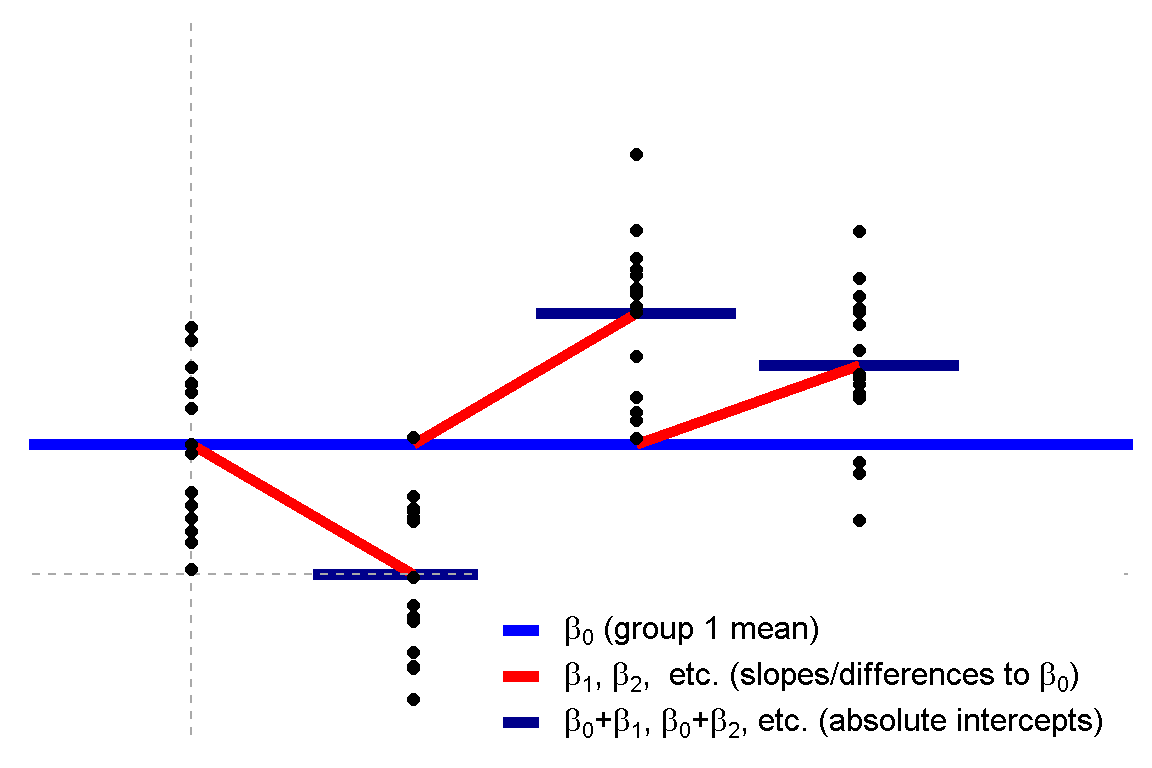變異數分析 |Regression|ANOVA| |---|---| ||| ---- ### 線型模型 ||Regression|ANOVA| |---|:---:|:---:| |線性模型|$y = \beta_0 + \beta_1 x$|$y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + ...$| |$H_0$|$\beta_1 = 0$|$y = \beta_0$| ---- ### 變異數分解 |Regression|ANOVA| |:---:|:---:| |$\sum_i \sum_j (Y_{ij} - \bar{Y})^2 =$ <br> $\sum_j(\hat{Y} - \bar{Y})^2 + \sum_i \sum_j(Y_{ij} - \hat{Y})^2$|$\sum_i \sum_j (Y_{ij} - \bar{Y})^2 =$ <br> $\sum_j(\bar{Y}_j - \bar{Y})^2 + \sum_i \sum_j(Y_{ij} - \bar{Y}_j)^2$| |$SS_{Total} = SS_{Regression} + SS_{Residual}$|$SS_{Total} = SS_{Variable} + SS_{Residual}$| ---- ### 案例說明 - 邀請134位大學生，隨機分派評估五組朋友數各異的臉書用戶之社交吸引力 - [JASP示範檔案](https://osf.io/ydz4p/);[jamovi示範檔案](https://osf.io/v26br/)  ---- ### 分析之前 - 研究者預期的組間差異，會是什麼樣子？ - 還沒收集資料前會怎麼想？ - 臉友數越多越受歡迎，評分越高 - 看到資料，做分析前會怎麼想？ - 300之後，似乎差不多 - 300似乎是最高分 - ANOVA的分析結果，能確實幫助研究者評估嗎？ ---- ### [變異數分析的考驗力分析](http://shiny.ieis.tue.nl/anova_power/)  ---- ### 報表解讀 |ANOVA|| |---|---| |General Linear Model|| ---- ### 適用性檢定 - 組間變異同質(Homogenerity) - 樣本分佈常態(Normality) ---- ### 殘差變異的抽樣分佈 - 符合F機率分佈  ---- ### 分析後報告 經過134位大學生分組評價五組臉書使用者公開資料，交友數102人得到最低社交吸引力評分(M = 3.82, SD = 1.00)，以設定的型一錯誤率不超過.05來看，五組之間的差異是明顯的： $F(4,129) = 4.14, MSE = 1.20, p = .003, \eta_p^2 = 0.114$。 ---- ### 分析風險 |任兩組之間t檢定|ANOVA| |---|---| |$C_2^5 \times .05$|.05| ---- ### 簡介多重比較 - [jamovi示範檔案](https://osf.io/v26br/)操作