# Sobre las geodesicas en superficies de revolucion
Presentación de geometría diferencial

de **Alvaro Martínez Ramírez**

---

## Alexis Claude Clairaut
**(1713-1765)**
Matemático y astrónomo de la época de la ilustración francesa.

<div class="r-stack">
<span ><img class="fragment fade-out" src="https://i.pinimg.com/originals/0f/5f/6f/0f5f6ff6255f22afcd7b036fa6d3eed9.jpg"/>
<span class="fragment current-visible">
no ese tipo de ilustración francesa!</span> </span>
<img class="fragment" src="https://mathshistory.st-andrews.ac.uk/Biographies/Clairaut/Clairaut.jpeg">
</div>

----

<div class="r-stack">
<img class="fragment fade-out" src="https://cdn11.bigcommerce.com/s-wefngua/images/stencil/1280x1280/products/767/2779/claieaut2__92271.1420134325.jpg"/>
<img class="fragment" src="http://www.mathouriste.eu/Clairaut/prem_article_extr.JPG" />
<img class="fragment" src="" />
<img class="fragment" src="" />
<!--img class="fragment" src="" /-->
</div>

Note:
Durante el desarrollo del cálculo diferencial, uno de los principales problemas a resolver era el movimiento de los astros bajo la gravedad de los planetas y el sol.

Es en ese contexto que llegó el niño Clairaut como el matemático más joven en ser aceptado dentro de la academia de las ciencias de Paris, a los 13 años, con el trabajo titulado *Quatre problèmes sur de nouvelles courbes*. [^1]

[^1] https://www.maa.org/press/periodicals/convergence/the-four-curves-of-alexis-clairaut

https://www.maa.org/book/export/html/2411028

*Sobre la forma de la tierra*
https://www.geology-books.com/rare-science-book-clairaut-alexis-claude-theorie-de-la-figure-de-la-terre-1743/

https://en.wikipedia.org/wiki/Alexis_Clairaut

----

$$ y = xy' + f(y')$$

<img src="http://www.mathouriste.eu/Clairaut/Parabola_env.gif" width="80%"/>

Note:
A lo largo de su vida, Clairaut investigó y desarrolló ecuaciones diferenciales que permitiran entender la trayectoria de cuerpos en orbita de planetas, logrando resultados trascendentes para la geometría (como el teorema que lleva su nombre sobre evolutas de ecuaciones diferenciales), geología (con un trabajo sobre la forma de la tierra según la medida de la gravedad) y astronomía.

----

<img src="https://2.bp.blogspot.com/-JyxA1iukjJI/UNeP708lCXI/AAAAAAAAAtw/vTeZMsgywvc/s1600/Leonhard%2BEuler.jpg" width="30%"/> <img src="https://i.pinimg.com/originals/45/f6/cb/45f6cb587883b090a745712756c0cda6.jpg" width="22%" /> <img src="https://4.bp.blogspot.com/-kv_bYFGT5ik/VQX_gU_p0NI/AAAAAAAAAcc/2aFOHkhxF5I/s1600/Johann_Bernoulli2.jpg" width="25%"/></span>

Note:
Trabajó en contacto directo con muchos de los matemáticos mas prominentes de su época como Euler, Johann Bernoulli, Maupertuis y d'Alambert [^2].

[^2] https://mathshistory.st-andrews.ac.uk/Biographies/Clairaut/

http://www.mathouriste.eu/Clairaut/Clairaut.html

----

<img src="https://milestone-books-de.cdn.bibliopolis.com/pictures/001995_1.jpg?auto=webp&v=1523105473" width="40%"/> <img src="https://milestone-books-de.cdn.bibliopolis.com/pictures/001995_4.jpg
" width="47%"/>

libro *Théorie de la lune*
https://www.milestone-books.de/pages/books/001995/alexis-claude-clairaut/theorie-de-la-lune-deduite-du-seul-principe-de-lattraction-reciproquement-proportionnelle-aux

Note:
Aunque en su época no existía aun el formalismo hamiltoniano de la mecánica, sus cálculos permitieron entender la dinámica celeste desde un punto de vista geométrico y variacional. Poco tiempo después J.L.Lagrange, también francés, logró avances fundamentales en mecánica celeste y geometría que permitieron llegar a dicho formalismo.

----

## Relación de Clairaut

$$R \cdot cos(\alpha) = c_{cte}$$


Note:
En cada punto de una geodésica sobre una superficie de revolución, se cumple una relación entre la distancia $R$ al eje de rotación de la superficie y el ángulo $\alpha$ que se forma entre la tangente a la geodésica y la tangente a rotación de la superficie.

----

## Interpretacion geométrica

----

### Superficies de revolucion

<div class="r-stack">
<img class="fragment fade-out" src="https://upload.wikimedia.org/wikipedia/commons/5/5d/Eug%C3%A8ne_Delacroix_-_Le_28_Juillet._La_Libert%C3%A9_guidant_le_peuple.jpg" alt="Eugène Delacroix - Le 28 Juillet. La Liberté guidant le peuple.jpg" height="480" width="598">

<img class="fragment current-visible" src="https://media.springernature.com/full/springer-static/image/chp%3A10.1007%2F978-3-319-11773-7_2/MediaObjects/322269_1_En_2_Figb_HTML.gif" height="480" alt="superficie de revolución"/>

<img class="fragment" src="https://catiadoc.free.fr/online/icmug_C2/images/SurfaceOfRevolution_types.gif" width="80%"/>

</div>

Note:
las superficies de revolución se pueden definir de la forma mas elemental como la superficie que resulta de girar una curva plana al rededor de una recta llamada eje. Esto se puede extender a una abstracción en la que se parametriza la superficie por el ángulo de rotación y la altura sobre dicho eje.

----

### Geodésicas
**imagen de curvas y longitud de arco con plano tangente**
$$ \int |\gamma'| dt $$

$$ \int \sqrt{\phi_{\gamma}^{*}(\gamma')^2 } dt $$

Note:
**falta**
- longitud de arco
- cuando la superficie está parametrizada

----

¿Cómo minimizamos la longitud?


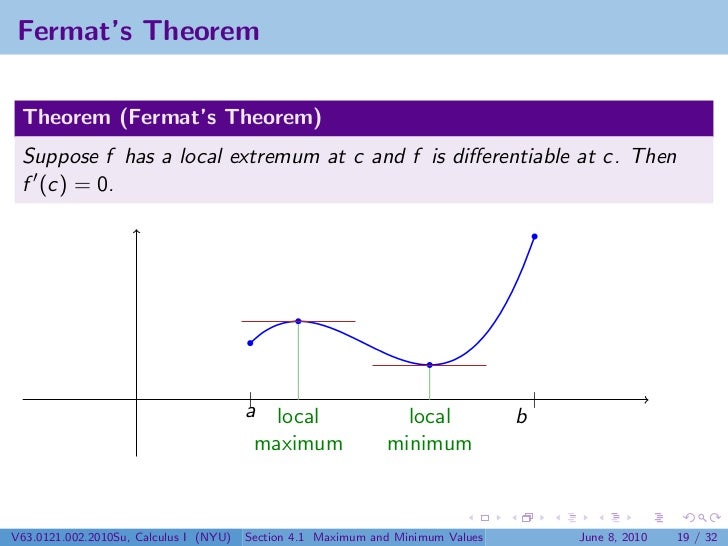
Note:
- imagen de punto mínimo en función
- plantear el problema de que no se miniza sobre un argumento, sino sobre un espacio de funciones

---

## Lagrange y el principio de acción estacionaria


Note:
- Maupertuis ya pensaba en problemas de optimización y estableció en geometría el llamado principio de Maupertuis
- Fermat lo había observado para optica
- Lagrange lamentablemente no conoció personalmente a Clairaut
- planteó el formalismo necesario para expresar geometricamente los problemas de mecánica
- La formulación lagrangiana significó una dirección fundamental para estudiar la realidad bajo la luz del análisis variacional. En este sentido una gran cantidad de los problemas de física se reducen a encontrar el funcional que describe geométricamente la realidad.
- Las geodesicas caben perfectamente en este marco de pensamiento

----

### principio de minima acción

$$ S = \int_{\gamma} L(\gamma, \gamma')dt$$

$$ \frac{\delta S}{\delta \gamma} = 0$$

Note:
- parece que la realidad evoluciona solamente hacia donde toma lo menos de un cierto funcional que involucra solamente la energía del sistema en cuestión.

- En física, la funcion lagrangiana $L$ se establece según el problema

----

### Cálculo variacional

si $\forall f$, tenemos que
$$\int f g \ dt = \langle f, g \rangle = 0$$
entonces $g= 0$ en todos los puntos

Note:
- lema fundamental del cálculo variacional
- el espacio de funciones es un espacio extremadamente grande, para asegurar que se cumplan algunos teoremas se le aplican restricciones (soporte compacto, continuidad, etc...)

----

##### Minimmizar un funcional
sobre una curva


Note:
- tomar una curva $\gamma$ y una variación muy cercana a ella
$\gamma + \varphi$
donde $|\varphi| < \epsilon$
- se puede evaluar el funcional con un solo argumento real
$$l \to \gamma + l\varphi$$
- teniendo fija la variacion $\varphi$, el funcional solo depende de $l$

----

### Ecc. de Euler-Lagrange

$$\frac{d }{d t}\left( \frac{\partial L}{\partial \dot \gamma}\right) - \frac{\partial L}{\partial \gamma} = 0 $$

Note:
- aplicando el lema fundamental a todas las variaciones posibles de una curva fija, resulta que el funcional solo se minimiza si la derivada es cero en cada punto
- haciendo manipulaciones simbólicas, llegamos a la ecuacion de identidad con cero de
$$ \Delta L/ \Delta l = 0$$

---

## Emmy Nöther

**imagenes de Noether, hilbert, gotinga y princeton**

Note:
Emmy Nöther fue la mujer mas importante para las matemáticas según Hilbert, Lefshetz y otros. Se graduó de Gotinga y tomó el lugar de otros profesores por que las autoridades de la universidad no permitían que una mujer fuera contratada.
En los primeros años de su trabajo como profesora, se dedicó a la búsqueda de invariantes de grupos, junto con otro profesor que le cedía su lugar en las clases y Hilbert.
Mas tarde se dedicó mas al desarrollo del álgebra abstracta que en ese momento se estaba replanteando.

----

### Leyes de conservación y simetrías



Note:

Los fisicos han observado desde el principio del estudio de la mecánica que en muchas situaciones aparecen cantidades que se conservan durante la evolución del movimiento de un conjunto de masas. A estos fenómenos les llamaron leyes de conservación (momento lineal, momento angular, energía, etc.). Sin embargo la explicación teorica más comprensiva apareció hasta que Nöther encontró que ciertos invariantes aparecen solamente por las condiciones de simetría del sistema donde sucede la dinámica. Esto es muy notable porque arroja una comprensión de la mecánica mas global y devela la naturaleza geométrica de la dinámica.

----

### Teorema de Nöther
![Emmy](https://upload.wikimedia.org/wikipedia/commons/e/e5/Noether.jpg "Emmy Nöther" =200x) ![imag](https://upload.wikimedia.org/wikipedia/commons/f/f5/Noether_theorem_scheme.png "" =300x)

$$ \frac{\partial \tau_\alpha}{\partial\alpha} \cdot \frac{\partial L}{\partial \dot \gamma} $$

Note:
https://en.wikipedia.org/wiki/Emmy_Noether
https://en.wikipedia.org/wiki/Noether%27s_theorem

---

## Conclusiones (resultados?)

https://sagemath.org/
(el sistema de cálculo simbólico)

----

### Aplicaciones a superficies especiales

----

#### Toro

----

#### Pseudoesfera

----

#### Soluciones numéricas