---
tags: vaje, or, grafi
hackmd: https://hackmd.io/29v0PupJRPOGccV0sV2i2g
plugins: mathjax
---
# Operacijske raziskave - vaje 17.5.2021
---
## Floyd-Warshallov algoritem
```python
class UtezenDigraf(Digraf):
...
def floydWarshall(G):
razdalja = {(u, v): 0 if u == v else float('inf')
for u in G.vozlisca() for v in G.vozlisca()}
stars = {(u, v): None for u in G.vozlisca() for v in G.vozlisca()}
for u in G.vozlisca():
for v, r in G.utezeniSosedi().items():
razdalja[u, v] = r
stars[u, v] = u
for w in G.vozlisca():
for u in G.vozlisca():
if razdalja[u, w] + razdalja[w, u] < 0:
raise ValueError("graf ima negativen cikel")
for v in G.vozlisca():
r = razdalja[u, w] + razdalja[w, v]
if r < razdalja[u, v]:
razdalja[u, v] = r
stars[u, v] = stars[w, v]
return (razdalja, stars)
```
Časovna zahtevnost: $O(n^3)$
* Dijkstrov algoritem (s kopico) iz vsakega vozlišča posebej: $O(mn \log n)$ je hitrejši, če velja $m = o(n^2/\log n)$ in nimamo negativnih uteži
---
### Naloga 1
S pomočjo Floyd-Warshallovega algoritma poišči najkrajše poti med vsemi pari vozlišč.

----
| | A | B | C | D | E | F | G | H |
| - | - | - | - | - | - | - | - | - |
| A | 0 | 3/A | 10/B | 3/C | 12/B | 1/G | 2/H | 7/D
| B | | 0 | 7/B | 0/C | 9/B | -2/G | -1/H | 4/D
| C | | 2/D | 0 | -7/C | 11/B | -3/G | -8/H | -3/D
| D | | 9/D | 16/B | 0 | 18/B | -2/G | -1/H | 4/D
| E | | 10/D | 17/B | 1/E | 0 | -1/G | 0/H | 5/D
| F | | | | | | 0 | 8/F
| G | | | | | | -1/G | 0
| H | | | | | | -6/G | -5/H | 0 |
---
## Uporaba algoritmov na grafih
### Naloga 2
Denimo, da imamo neusmerjen graf $G = (V, E)$, katerega vozlišča predstavljajo mesta, povezave pa predstavljajo ceste, ki jih povezujejo. Za vsako povezavo $e \in E$ poznamo njeno dolžino ${\ell_e}$ (v kilometrih).
Priti želimo iz mesta $s$ v mesto $t$. V vsakem mestu je bencinska črpalka, ob cestah pa teh ni. Žal imamo na voljo samo star avto, ki lahko s polnim rezervoarjem prepelje le $L$ kilometrov.
1. Zapiši algoritem, ki v linearnem času poišče pot, ki jo lahko prevozimo z našim avtom, oziroma ugotovi, da ta ne obstaja.
2. Izkaže se, da z našim avtom te poti ne moremo prevoziti, zato se odločimo za nakup novega. Zapiši algoritem, ki v času $O(m \log n)$ določi najmanjše število prevoženih kilometrov, ki naj jih avto zmore z enim polnjenjem, da bo pot od $s$ do $t$ mogoča.
----
1. * Konstruiramo graf $G' = (V, E')$, kjer je $E' = \lbrace e \in E \mid {\ell_e} \le L \rbrace$
* Uporabimo BFS ali DFS na $G'$ z začetkom v $s$
* Če dosežemo vozlišče $t$, potem ustrezna pot obstaja
* Časovna zahtevnost: $O(m)$
2. Varianta Dijkstrovega algoritma:
```python
def minPrevozenih(G, s, t):
Q = Kopica({v: -float('inf') if v == s else float('inf')
for v in G.vozlisca()})
min_prevozenih = {}
stars = {s: None}
while len(Q) > 0:
v, d = Q.pop()
min_prevozenih[v] = d
if v == t:
return (min_prevozenih[t], stars)
for w, l in G.utezeniSosedi(v).items():
if w in min_prevozenih:
continue
r = max(d, l)
if r < Q[w]:
Q[w] = r
stars[w] = v
raise ValueError("končnega vozlišča ni mogoče doseči")
```
---
### Naloga 3
Oviratlon je tekalna preizkušnja na 8 do 10 kilometrov dolgi poti z različnimi ovirami. Zanima nas, na koliko različnih načinov lahko pridemo od štarta do cilja. Dan je utežen usmerjen acikličen graf $G$ ter vozlišči $s$ in $t$, ki predstavljata štart oziroma cilj. Uteži na povezavah nam predstavljajo, na koliko načinov jih lahko prečkamo.
1. Reši nalogo za sledeči graf.
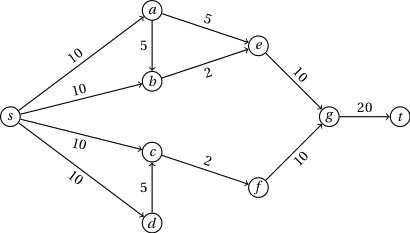
2. Zapiši algoritem, ki reši dani problem. Kakšna je njegova časovna zahtevnost?
----
```python
def oviratlon(G, s, t):
nacini = {v: 1 if v == s else 0 for v in G.vozlisca()}
for u in G.topoloskoUrejanje():
for v, st in G.utezeniSosedi(u).items():
nacini[v] += nacini[u] * st
return nacini[t]
```
Časovna zahevnost: $O(m)$
| s | a | b | d | c | e | f | g | t |
| - | - | - | - | - | - | - | - | - |
| 1 | 10 | 60 | 10 | 60 | 170 | 120 | 2900 | 58000 |
---
### Naloga 4
Dan je neusmerjen utežen graf $G = (V, E)$ z nenegativnimi cenami povezav ${L_e}$ ($e \in E$). Naj bosta $A$ in $B$ disjunktni množici povezav, tako da velja $E = A \cup B$. Želimo najti najcenejšo *alternirajočo* pot med danima vozliščema $s, t \in V$ - torej takšno, v kateri se povezave iz $A$ in iz $B$ izmenjujejo (ni pomembno, ali začnemo oziroma končamo s povezavo iz množice $A$ ali $B$). Posamezno vozlišče se lahko v alternirajoči poti pojavi tudi večkrat.
1. Predlagaj čim učinkovitejši algoritem za reševanje danega problema. Kakšna je njegova časovna zahtevnost?
**Namig:** grafu $G$ priredi usmerjen graf $G'$, v katerem bodo vse poti od $s$ do $t$ ustrezale alternirajočim potem v $G$. Po potrebi lahko vozlišča tudi podvojiš.
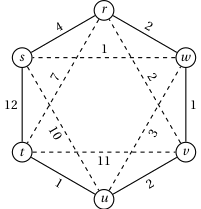
2. S svojim algoritmom poišči najcenejšo alternirajočo pot od $s$ do $t$ na spodnjem grafu. Povezave iz množice $A$ so označene s polno, povezave iz množice $B$ pa s črtkano črto. Iz rešitve naj bo jasno, kako poteka izvajanje algoritma.
 Sign in with Wallet
Sign in with Wallet

