# 圖的抽象資料型態
## 定義
圖由兩種基本物組成: 邊(edge)、節點(vertex)
而邊則有兩種型態(有無方向)

## 表現方式
一張圖通常是使用點集合與邊集合的方式表示(手寫)，而在程式實作中通常只使用edge set(看情況)
| graph | vertex | edge |
| ----- | ------------- |:----------------------------------- |
| a | 0,1,2,3 | (0,1),(0,2),(0,3),(1,2),(1,3),(2,3) |
| b | 0,1,2,3,4,5,6 | (0,1),(0,2),(1,3),(1,4),(2,5),(2,6) |
| c | 0,1,2 | <0,1>,<1,0>,<1,2> |

*tips:* 在有向圖中，edge set 中的紀錄也會有方向(通常由前指向後<前,後>)

## Constraints (通常禁止以下的內容)
1. self edge
:::spoiler
指那些由A指向A的邊，也稱 self loop
EX : (A,A)、<C,C>
<img src="https://github.com/baiyanchen8/hackmd-image/blob/main/%E5%9F%BA%E7%A4%8E%E8%B3%87%E6%96%99%E7%B5%90%E6%A7%8B/chap6/self_loop.jpg?raw=true" width="" height="288">
:::
3. multigraph
:::spoiler
擁有**多重邊**的圖即稱為 mutigraph
<img src="https://github.com/baiyanchen8/hackmd-image/blob/main/%E5%9F%BA%E7%A4%8E%E8%B3%87%E6%96%99%E7%B5%90%E6%A7%8B/chap6/multigraph.jpg?raw=true" width="" height="288">
:::

## 圖的各種表示法
### 相鄰矩陣 (Adjacency Matrix)
假設共有 N 個 Vertex，使用一個N$\times$N的矩陣，並用0表示不相鄰、1表示相鄰。
:::spoiler 舉例
使用$G_3$舉例
| x\y | 0 | 1 | 2 |
| --- |:--- | --- | --- |
| 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |

*tips:* 在這裡有方向性(y$\rightarrow$x)
:::
#### 優點
對於尋找A,B任意兩點之間是否相鄰非常快，只需要$O(1)$
#### 缺點
空間複雜度為$O(N^2)$，且所有需要遍歷的算法都需要比較大的時間複雜度

### 相鄰串列 (adjacency list)

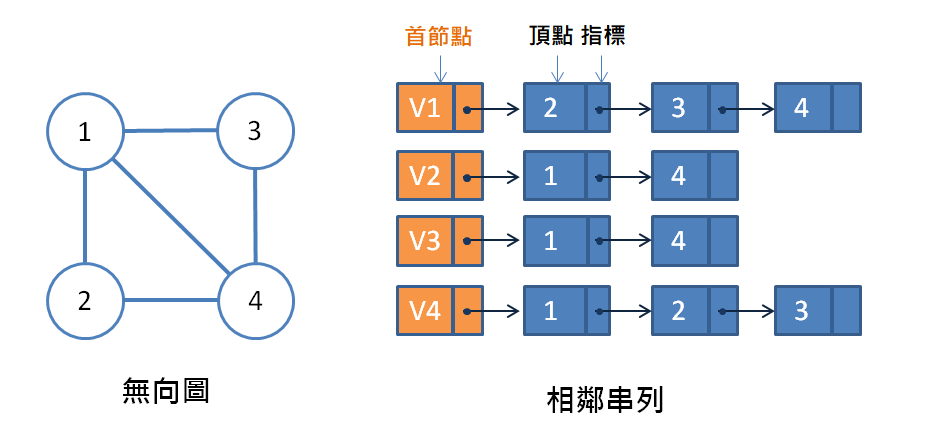
### 相鄰多元串列 (Adjacency Multilist)

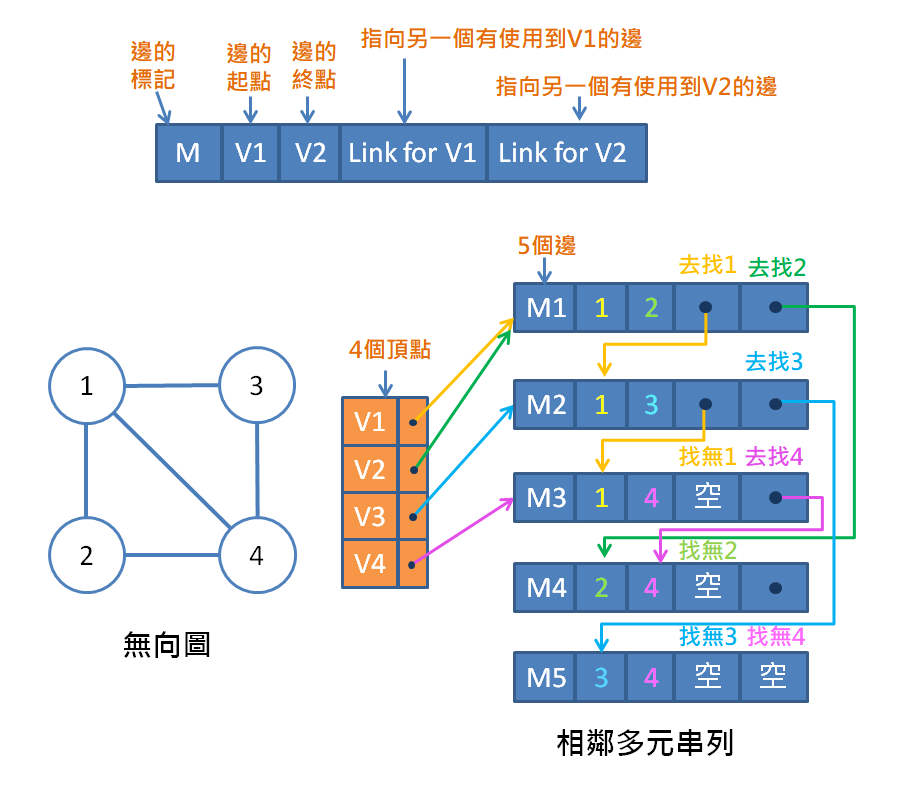
### 索引表 (Index Table)
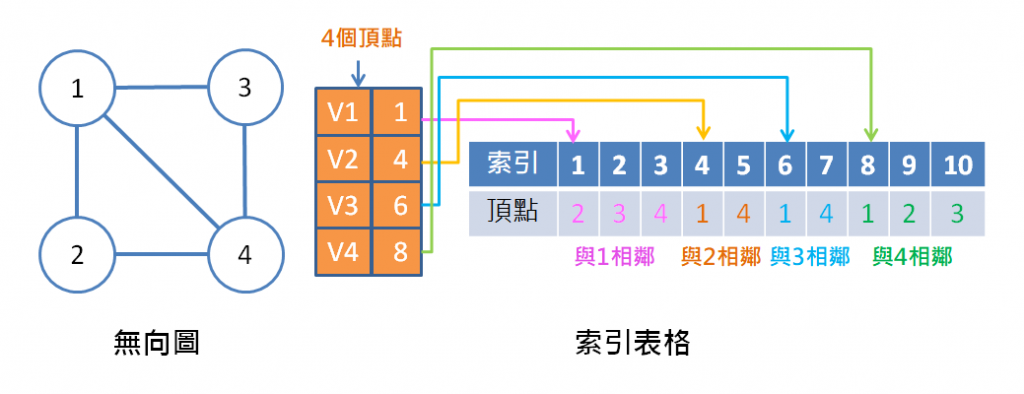
# 圖的各種基本名詞
1. 完全圖 full graph
:::spoiler
一個有*n*個邊的無向圖中，最多可能有$\frac{n(n-1)}{2}$個邊(*握手問題*)，而一個擁有最多可能邊的無向圖則稱為無向圖
### **Example**
<img src="https://github.com/baiyanchen8/hackmd-image/blob/main/%E5%9F%BA%E7%A4%8E%E8%B3%87%E6%96%99%E7%B5%90%E6%A7%8B/chap6/fullgraph.jpg?raw=true" width="" height="288">
:::
1. 子圖 sub-graph
:::spoiler 說明
通過將原本的圖拆分，所獲得的圖即為 sub-graph
:::
1. 迴圈 circle
:::spoiler 說明
由一段頭尾相同的路徑組成
:::
1. 連通 connect
:::spoiler 說明
指一張圖中，若u&v之間存在至少一條路徑，即為連通
:::
1. 連通元件 connect components
:::spoiler 說明
連通元件是指在一個圖形或網路中，能夠互相連接的元素或節點集合，這些元素之間可以透過路徑相互到達。
:::
1. 強連通圖 strongly connected components
:::spoiler 說明
強連通圖是指在*有向圖*中，任意兩個節點之間都存在互相到達的路徑，也就是說，圖中的任意兩個節點都是彼此可達的。
:::
1. 弱連通圖 weak connected components
:::spoiler 說明
如果將一個*有像圖*所有有向邊替換為無向邊之後的無向圖是連通的，則稱為弱連通圖。
:::
1. 分支度
:::spoiler 說明
1. 無向圖
所有相連邊的數量
3. 有向圖
有向圖的分支度分為入分支度 & 出分支度，就是將指向節點的邊&指出節點的邊分開計算。
:::

# 圖的基本運算

## Deepth First Search (深度優先算法)

從字面意義上可知，是優先探索深度的算法

int visited[num_vertex]; // 假設 non visited 為 0 , visited 為1 
int edge [num_vertex][2];//假設未使用的edge內容為(-1,-1)
void dfs(int now){
    visited[now]=1;
    printf("%d ",now);
    int i;
    for (i=0;i<num_vertex;i++){
        if (edge[i][0]==-1 || edge[i][1]==-1)
            continue;
        if (edge[i][0]==now && visited[edge[i][1]]==0)
            dfs(edge[i][1]);
        if (edge[i][1]==now && visited[edge[i][0]]==0)
            dfs(edge[i][0]);
    }
}

## Breadth First Search

int visited[num_vertex]; // 假設 non visited 為 0 , visited 為1 
int edge [num_vertex][2];//假設未使用的edge內容為(-1,-1)void bfs(int now){
void bfs(int now){
    addqueue(now);
    int tmp;
    while (queue){
        tmp = dequeue();
        if (tmp ==-1){
            break;
        }
        visited[tmp] = 1;
        printf ("%d ", tmp);
        int i;
        for (i = 0; i < num_vertex; i++){
            if (edge[i][0] == -1 || edge[i][1] == -1)
                continue;
            if (edge[i][0] == tmp && visited[edge[i][1]] == 0)
                addqueue(edge[i][1]);
            if (edge[i][1] == tmp && visited[edge[i][0]] == 0)
                addqueue(edge[i][0]);
        }
    }
}

## 連通元件
通過 dfs or bfs 尋找就可以了。

void connected(){
    bfs();
}

## 生成樹
當選擇圖中一個頂點，然後使用某種算法遍歷所有頂點，把所有其中經歷的路徑記錄下來便是生成樹

## 雙連通元件((bi-connected components))
articulation point : 將*連通圖G*中某一*節點v*刪除會出現多個(>1)連通圖，該節點極為連接點(articulation point)

### low 公式
low(n)=min{dfn(n)
&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;,min{low(w)\|當w為n的child on dfs tree}
&emsp;&emsp;&emsp;&emsp;&emsp;&emsp;,min{dfn(w)\|當(w,n)為back edge}}

### code
不想寫 ......

# 最小花費生成樹(Minimum spanning tree)
## greedy method

# 最短路徑與遞移封閉

# 活動網路