# 2018q1 Homework3 (list)
contributed by <`ujiet`>
## 生日悖論
- **如何透過近似的運算式,估算上述機率計算呢?附上有效的 LaTeX 算式。**
根據 [Extensions of the birthday surprise](https://www.sciencedirect.com/science/article/pii/S0021980067800759) 此篇的內容,尋找 $E(n,k)$ 函數當中 $E(365,2)$ 的答案即為所求。其中 $n$ 可視為有幾種相異物,我們在 $n$ 中可重複的挑選物品,直到發現其中一物已挑出了 $k$ 次才停止,而 $E(n,k)$ 即為預期完成所需要的次數。
假設一個 Trucating Operation --- $T_k$,使得多項式中大於 $k$ 次的項皆被消除,則我們可以得到 $$E = \sum_{N=0}^{\infty}\ \ T_k\{(x_1 + x_2 + \cdots + x_n)^N\}]_{\frac{1}{n},\frac{1}{n},\cdots,\frac{1}{n}}$$ 為 $E$ 的期望值,也就是 $N$ 次選取後失敗的機率之總和。其中 $(x_1 + x_2 + \cdots + x_n)^N$ 為經過 $N$ 次選取所得之生成函數。考慮以下級數: $$F(t) = \sum_{N=0}^{\infty}\ \ T_k\{(x_1 + x_2 + \cdots + x_n)^N\}\cfrac{t^N}{N!} = S_k(x_1t)S_k(x_2t)\cdots S_k(x_nt)$$ 其中 $S_k(x)$ 為 $e^x$ 的 $k$-th partial sum。由於 $$1 = \int^{\infty}_{0} \cfrac{t^N}{N!}\ e^{-t}dt$$ 故可得到 $$\sum_{N=0}^{\infty}\ \ T_k\{(x_1 + x_2 + \cdots + x_n)^N\} = \int^{\infty}_{0} F(t)\ e^{-t}dt$$ 代入 $x_i = 1/n$ ,可得 $$E(n,k) = \int^{\infty}_{0} [S_k(\frac{t}{n})]^n\ e^{-t}dt$$
為了求取近似值,設 $t = n^{1-1/k}u$,代入上式:
$$E = n^{1-1/k}\int^{\infty}_{0} \{S_k(un^{-1/k})e^{-un^{-1/k}}\}^ndu$$
又當 $n \rightarrow \infty$ 時,
$$\{S_k(un^{-1/k})e^{-un^{-1/k}}\}^n \rightarrow e^{-u^k/k!}$$
所以可得到
$$\lim_{n\rightarrow\infty}\cfrac{E(n,k)}{n^{1-1/k}} = \sqrt[k]{k!}\ \Gamma(1+1/k)$$
故當 $n\rightarrow \infty$ 時,近似式為:
$$E(n,k) \sim \sqrt[k]{k!}\ \Gamma(1+1/k)\ n^{1-1/k}$$
求得結果:
$$E(365,2) \approx \sqrt{2}\ \Gamma(\frac{3}{2})\sqrt{365} \approx 23.94$$
- **[Birthday problem](https://en.wikipedia.org/wiki/Birthday_problem) 對資訊安全的影響在哪些層面?**
主要影響於加密雜湊函數的破解。Birthday problem 告訴我們輸入集合過大或是輸出值長度過短的雜湊函數可能被輕易的破解。
一個好的 hash function 應該盡量減少 collision,也就是盡量讓輸出的值分散。而是否發生碰撞主要由 **輸入集合的大小(size)** 與 **輸出值的大小(length)** 所共同決定,故避免碰撞的方法,可根據輸入集合的大小選取輸出合適長度 hash value 的 hash function。
從 [wiki](https://en.wikipedia.org/wiki/Birthday_attack) 可得知若 hash value 有 $H$ 種可能,則產生一次碰撞大約需要 $1.25\sqrt{H}$ 次的嘗試。對於 n-bit 的值而言,可以 $2^{\frac{n}{2}}$ 來計算。舉例來說,使用一個 64 位的 hash function,如果產生每個 hash value 的可能性是相同的,那麼只需大約 $5.1 \times 10^9$ 次嘗試就有約 50% 的機會發生碰撞。下圖顯示不同位元數的值所需的嘗試次數。
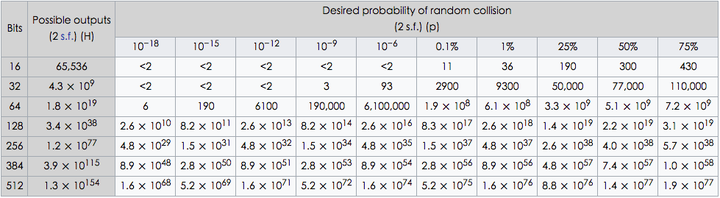
故在使用加密雜湊函數時,輸入集合的大小應盡量保持在安全的範圍內。例如使用 128-bit 的 MD5 時,將輸入集合大小控制在 $8.2 \times 10^{11}$ 個以內,可將碰撞機率降低至 $10^{-15}$ 以下。
- [參考資料](https://www.zhihu.com/question/54307104)
- **像是 [Random Number Generator](http://stattrek.com/statistics/random-number-generator.aspx) 這樣的產生器,是否能產生「夠亂」的亂數呢?**
---
## Linux 風格的 linked list
- 重點整理
- 好的程式設計品味 - The fewer conditions you test for, the better your code “tastes”.
- [git merge 與 rebase 的選擇](https://github.com/geeeeeeeeek/git-recipes/wiki/5.1-%E4%BB%A3%E7%A0%81%E5%90%88%E5%B9%B6%EF%BC%9AMerge%E3%80%81Rebase-%E7%9A%84%E9%80%89%E6%8B%A9)
- link list 的刪除是**常數時間**
- **為何 Linux 採用 macro 來實作 linked list?一般的 function call 有何成本?**
Linux 在很多地方都會使用 link list 來解決問題,因此使用 macro 不但可以統一 link list 的形式,也可以使用統一的 function 來操作,類似物件導向語言裡的資料封裝。
一般 function call 使用時,須先將原函式的資訊(parameter, local variable, return address)等,存進 stack 後,再進行所要的函式,在遞迴呼叫的時候需要花費相當大的成本在存取 stack。若採用 macro 則可在編譯之前展開所需函式,減少存取 stack 的成本,但缺點是增加 code 的長度且難以 debug。
- **Linux 應用 linked list 在哪些場合?舉三個案例並附上對應程式碼,需解說以及揣摩對應的考量。**
1. 在 Process list 中,常常使用到,例如 Linux 的 waiting queue
```
struct wait_queue_head {
spinlock_t lock;
struct list_head task_list;
};
typedef struct wait_queue_head wait_queue_head_t;
```
spinlock_t 為互斥控制的欄位,因為 waiting queue 有被 interrupt handler 和 kernel functions 修改的可能,所以須防止 kernel 的 concurrent access。
```
struct wait_queue {
unsigned int flags;
struct task_struct * task;
wait_queue_func_t func;
struct list_head task_list;
};
typedef struct wait_queue wait_queue_t;
```
每個在 waiting queue 裡的 element 代表一個 sleeping process。`task` 指向該 process 的 desciptor,而 `task_list` 指向等待同一個事件發生的 processes 。`flags` 用來識別該 process 是否為 exclusive,通常若只需喚醒一個 process ,系統會優先喚醒 nonexclusive process。
```
A process waiting for a resource that can be granted to just one process at a time is a typical exclusive process. Processes waiting for an event that may concern any of them are nonexclusive.
```
2. 在 Linux kernel 裡的 hash table 則是以 hlist 建構,也就是雙向非環狀鏈結串列。在 `list.h` 和 `hashtable.h` 中:
```
#define HLIST_HEAD_INIT { .first = NULL }
#define HLIST_HEAD(name) struct hlist_head name = { .first = NULL }
#define INIT_HLIST_HEAD(ptr) ((ptr)->first = NULL)
...
static inline void __hash_init(struct hlist_head *ht, unsigned int sz)
{
unsigned int i;
for (i = 0; i < sz; i++)
INIT_HLIST_HEAD(&ht[i]);
}
```
因為非環狀,所以一開始的指標指向 NULL,再根據所需的 size(sz) 和 height(ht) 建立 table。
3. 在 glib 中的所使用的 glist 也是以 doubly link list 呈現。結構如下
```
struct GList {
gpointer data;
GList *next;
GList *prev;
};
```
和 linux list 不同的地方在於多了一個 gpointer,可指向任何型態的資料。
- [Glib Reference Manual](https://people.gnome.org/~desrt/glib-docs/index.html)
- **GNU extension 的 typeof 有何作用?在程式碼中扮演什麼角色?**
根據[此篇](https://gcc.gnu.org/onlinedocs/gcc/Typeof.html)中所提到,typeof 可以得到其<s>引數</s>參數的資料型別。其引數可為表示式或直接為資料名稱。
:::warning
parameter 翻譯為「參數」
:notes: jserv
:::
一般來說,typeof 常用於連接 statement expressions,可以保障資料型別的正確性。下面程式碼展現了如何實作一個安全的 "maximum" macro:
```
#define max(a,b) \
({ typeof (a) _a = (a); \
typeof (b) _b = (b); \
_a > _b ? _a : _b; })
```
注意底線的使用是為了避免和原來的參數產生衝突。如[這裡](https://gcc.gnu.org/onlinedocs/gcc/Statement-Exprs.html#Statement-Exprs)提到,若沒有加上底線,參數中的 a 或 b 其中之一可能會計算兩次,而若此參數有其他副作用則可能產生不可預期的結果。其中的 `({ ... })` 為 GNU C 的特殊用法,用來表示一個 compound statement,為多個 statement 的集合。conpound statement 在多個 statement 之後,最後需放一個 expression,其值即為該 compound statement 的值。
- **解釋以下巨集的原理:**
```
#define container_of(ptr, type, member) \
__extension__({ \
const __typeof__(((type *) 0)->member) *__pmember = (ptr); \
(type *) ((char *) __pmember - offsetof(type, member)); \
})
```
[查詢](https://stackoverflow.com/questions/5323478/how-to-use-extension-and-typeof-in-a-minified-example-in-c)之後發現 ```__extension__``` 的作用為避免一些 GNU C extension 所造成的 warning。
```((type *) 0)->member``` 將數值 0 強制轉成指向 type 這個資料型別的指標後再指向其中的 member 成員。故此整行的作用為:宣告一個指向 member 的指標 __pmember,其值為 ptr。
下一行的 `offsetof()` 可以得到 member 與 type 起始點的偏移量,以 __pmember 的值減去後即可得該 type 的起始位址。
結論:利用 `container_of()`,只要知道某結構任一成員的位址,即可求包含該成員之結構的起始位址。
- [參考資料](https://myao0730.blogspot.tw/2016/09/linuxcontainerof-offsetof.html)
- **除了你熟悉的 add 和 delete 操作,`list.h` 還定義一系列操作,為什麼呢?這些有什麼益處?**
將此類抽象資料型別的各種操作事先在 header 定義好,如此一來在實作的時候,只需引入標頭檔即可進行各種操作,可達成類似資料封裝的概念。
- **`LIST_POISONING` 這樣的設計有何意義?**
在 `poison.h` 中,有以下程式碼:
```clike
/*
* Architectures might want to move the poison pointer offset
* into some well-recognized area such as 0xdead000000000000,
* that is also not mappable by user-space exploits:
*/
#ifdef CONFIG_ILLEGAL_POINTER_VALUE
# define POISON_POINTER_DELTA _AC(CONFIG_ILLEGAL_POINTER_VALUE, UL)
#else
# define POISON_POINTER_DELTA 0
#endif
/*
* These are non-NULL pointers that will result in page faults
* under normal circumstances, used to verify that nobody uses
* non-initialized list entries.
*/
#define LIST_POISON1 ((void *) 0x100 + POISON_POINTER_DELTA)
#define LIST_POISON2 ((void *) 0x200 + POISON_POINTER_DELTA)
```
由註解可發現,`LIST_POISON1` 和 `LIST_POISON2` 這些非空的指標在正常情況下會導致 page fault 的發生,可以用來測試結點是否已被正確地刪除。
- **linked list 採用環狀是基於哪些考量?**
在 linux 的 link list 中,許多操作都需要走訪 list 中的結點。使用雙向可以讓存取前一個結點更快速,而在環狀的結構下,我們只需一個 for loop 即可實作走訪的過程,且指標最後會回到串列的頭,減少實作的複雜性。另外,Linux 也有支援非環狀的串列,即為 hlist,通常用於空間需求大且不常存取到最後一個結點的場合,例如 hash table。
- **`list_for_each_safe` 和 `list_for_each` 的差異在哪?“safe” 在執行時期的影響為何?**
`list_for_each` 用於走訪一個串列裡的所有結點,但沒有任何其他的保護動作。在 `list_for_each_safe` 中,由於多一個 n 去指定 pos 的下一個結點,所以萬一 head 被刪除也不會有任何影響。
- **for_each 風格的開發方式對程式開發者的影響為何?**
- **提示:對照其他程式語言,如 Perl 和 Python**
- **程式註解裡頭大量存在 @ 符號,這有何意義?你能否應用在後續的程式開發呢?**
- **提示: 對照看 Doxygen**
Doxygen 是一開源的程式文件產生器,可幫助開發者撰寫註解。

此處的 @ 符號大部分為表示參數之用。更多用法可以參照 [Doxygen 手冊](http://www.stack.nl/~dimitri/doxygen/manual/index.html)。
- **`tests/` 目錄底下的 unit test 的作用為何?就軟體工程來說的精神為何?**
從最簡單的小功能一一的測試,可以在確保功能可行的狀況下逐步完成專案。不但可以減少發生錯誤的機會,也能加快工作的速度。
- [Twelve Benefits of Writing Unit Tests First](http://sd.jtimothyking.com/2006/07/11/twelve-benefits-of-writing-unit-tests-first/)
- **`tests/` 目錄的 unit test 可如何持續精進和改善呢?**
---
## 針對 linked list 的排序演算法
- **對 linked list 進行排序的應用場合為何?**
- **考慮到 linked list 在某些場合幾乎都是幾乎排序完成,這樣貿然套用 quick sort 會有什麼問題?如何確保在平均和最差的時間複雜度呢?**
- **能否找出 Linux 核心原始程式碼裡頭,對 linked list 排序的案例?**
- **透過 skiplist 這樣的變形,能否加速排序?**
- **研讀 How to find the kth largest element in an unsorted array of length n in O(n)?,比照上方連結,是否能設計出針對 linked list 有效找出第 k 大 (或小) 元素的演算法?**
- **linux-list 裡頭 examples 裡頭有兩種排序實作 (insertion 和 quick sort),請簡述其原理**
---
## Merge sort 實作
實作了很久才終於成功,程式碼如下:
```clike=
#include <assert.h>
#include <stdlib.h>
#include "list.h"
#include "common.h"
static uint16_t values[256];
static struct list_head *getMiddle(struct list_head *head)
{
if (head->next == head)
return head;
struct list_head *fast, *slow;
slow = fast = head;
while (fast->next != head && fast->next->next != head) {
fast = fast->next->next;
slow = slow->next;
}
return slow;
}
static void merge(struct list_head *head, struct list_head *newhead)
{
struct listitem *item1 = NULL, *item2 = NULL;
LIST_HEAD(temp);
while (!list_empty(head) && !list_empty(newhead)) {
item1 = list_first_entry(head, struct listitem, list);
item2 = list_first_entry(newhead, struct listitem, list);
if (cmpint(&item1->i, &item2->i) < 0)
list_move_tail(&item1->list, &temp);
else
list_move_tail(&item2->list, &temp);
}
list_splice_tail_init(head, &temp);
list_splice_tail_init(newhead, &temp);
list_splice_init(&temp, head);
}
static void list_msort(struct list_head *head){
if (list_empty(head) || list_is_singular(head))
return;
struct list_head *middle;
LIST_HEAD(newhead);
middle = getMiddle(head);
list_cut_position(&newhead, head, middle);
list_msort(head);
list_msort(&newhead);
merge(head, &newhead);
return;
}
int main(void)
{
...
list_msort(&testlist);
...
return 0;
}
```
main 函式裡頭和 `/examples` 裡的 `insert-sort.c` 的 main 幾乎一樣,只要把其中一行改掉就好。
getMiddle 函式可以得到 list 的中間點,運用了和龜兔賽跑相似的原理。先讓一個指標移動的速度是另一個指標的兩倍,則當快的完成一圈回到 head 時,慢的此時會恰好在 list 的中間。
將此 merge-sort.c 放進 `/tests` 裡,執行 make ,得到 Verified 即算成功。
```
CC tests/merge-sort.o
LD tests/merge-sort
*** Validating tests/merge-sort ***
[ Verified ]
```
---
- Reference
- Understanding the Linux Kernel, Daniel P. Bovet, 3rd Edition
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet