# 2017 q3 Homework08 - Natural merge sort contributed by <`Zixin`, `kevin550029`> :::danger **TODO**: * natural merge sort 的應用情境 ::: ## 目標 * 延續 [Natural merge sort 在特定硬體的加速](https://hackmd.io/s/B1_V03Vlg)，釐清之前的議題。需要完整的技術報告和錄影 ## 先備知識 ### Mergesort #### 參考資料 * [ALGORITHMS - MERGE SORT](http://www.bogotobogo.com/Algorithms/mergesort.php) * [Real-world sorting](http://www.cse.chalmers.se/edu/year/2016/course/DIT960_Data_structures/slides/8.pdf) #### 範例一 ![](https://i.imgur.com/MstWopF.png) * Partition: 對半切, 切到每個 array 只有一個元素 * Merge: 兩兩比大小進行合併, 每次比較皆由第一個元素開始比 (該 array 最小的數) 取最小的放在新的 array, 在原本的 array 中刪除該數字 再繼續比較兩個 array 的第一個數, 直到把兩個 array 中的數字都比完 #### 範例二 ![](https://i.imgur.com/jndUUgT.png) ![](https://i.imgur.com/bhrFAjE.png) ```clike= vector<int> mergeSort(vector<int> m) //傳入一組數列 { if (m.size() <= 1) //當傳入的數列長度小於等於一時，回傳數列本身 return m; vector<int> left, right, result; int middle = ((int)m.size()+ 1) / 2; //取得傳入數列的中間位置 //將中間位置之前的數字 push 進 left 的 vector for (int i = 0; i < middle; i++) { left.push_back(m[i]); } //將中間位置之後的數字 push 進 right 的 vector for (int i = middle; i < (int)m.size(); i++) { right.push_back(m[i]); } //遞回執行, 直到傳入的數列長度為一的時候中止, 並回傳數列本身(長度為一的數列) left = mergeSort(left); right = mergeSort(right); // 比較第一個數的大小, 合併兩個 vectors result = merge(left, right); return result; } ``` ## Natural Merge Sort 介紹 :::danger difference between two merge sort ( deal with odd number input ) [merge sort wiki - varient](https://en.wikipedia.org/wiki/Merge_sort) -> try to reducing space complexity & cost of copying use figures to explain ::: * Idea: Exploit pre-existing order by identifying naturally-occurring runs * 傳統的 Merge Sort 在進行合併之前，會先把數列的 list 切割成單一個 element ，而 Natural Merge Sort 則會將 list 切成一個一個 run (有序數列) * 簡而言之，Natural Merge Sort 是利用數據中**本身存在的有序數列 (升序或降序) 片段**, 來 **減少切割的次數** ![](https://i.imgur.com/CMnJcUG.png) 以上面的圖當例子，" 1 3 6 8 "是一個在原數列中，已排序好的子數列，在 Natural Merge Sort 中，這個數列可已被切割成一個單一的 run :::danger 我們觀察到兩種 Natural Merge Sort 的實作方式，下面會用兩個例子解釋 ::: ### 範例 第一個例子是來自於 [wiki - Natural merge sort](https://en.wikipedia.org/wiki/Merge_sort#Natural_merge_sort) 這個方法會先探訪一遍數列，並將有序數列切成多個 runs 再做合併 ``` Start : 3--4--2--1--7--5--8--9--0--6 Select runs : 3--4 2 1--7 5--8--9 0--6 Merge : 2--3--4 1--5--7--8--9 0--6 Merge : 1--2--3--4--5--7--8--9 0--6 Merge : 0--1--2--3--4--5--6--7--8--9 ``` 第二個例子是來自於 [淺談 merge sort](https://blog.kuoe0.tw/posts/2013/03/06/sort-about-merge-sort/) ，下方用他提供的演算法來解釋 * Algorithm 描述: 傳入要排序的 A 數列，宣告兩個數列空間 B 與 C，並設定數列 B 為使用中數列( CUR ) * 依序探訪原數列元素，並將元素放入使用中數列 B * 當目前的元素小於上一個元素時，並將該元素放入另一個數列 C * 不斷的重複上述步驟，直到所有元素都被探訪過，並分配到子數列 ```clike= function naturalMergeSort( A ): B, C are empty sequence //宣告空的兩個數列空間， B 與 C CUR refer to B //設定 B 為使用中數列 LAST = A[ 0 ] //設定 CUR 中最後一個數字為 A 的第一個數字 // first( A ) 與 LAST 比較, 較大則將 first( A ) 存入 CUR // 較小將 CUR 指向另一個 不在使用中 的數列空間, 並將 first( A ) 存入 CUR while A is not empty if first( A ) >= LAST append first(A) to CUR LAST = first( A ) A = rest( A ) else if CUR refer to B CUR refer to C else CUR refer to B LAST = first( A ) if B is empty or C is empty return // 當 A 被切割完成後, 傳入 B 和 C 繼續進行切割 // 直到其中一個傳入數列已變成有序數列 (不用再切割) naturalMergeSort( B ) naturalMergeSort( C ) A = merge( B, C ) ``` 假如 input 數列 A 為 1 3 4 2 7 5 8 0 9 第一輪切割後，B 和 C 分別為 B: 1 3 4 5 8 C: 2 7 0 9 再將 B 和 C 分別傳入 naturalMergeSort() 繼續進行切割 ## 比較 Natural Merge Sort 利用有序數列來減少傳統 Merge Sort 所需要的切割數量， 藉此來加速排序過程，但他在切割 run 時必須進行比較，這個過程也會耗費額外的時間。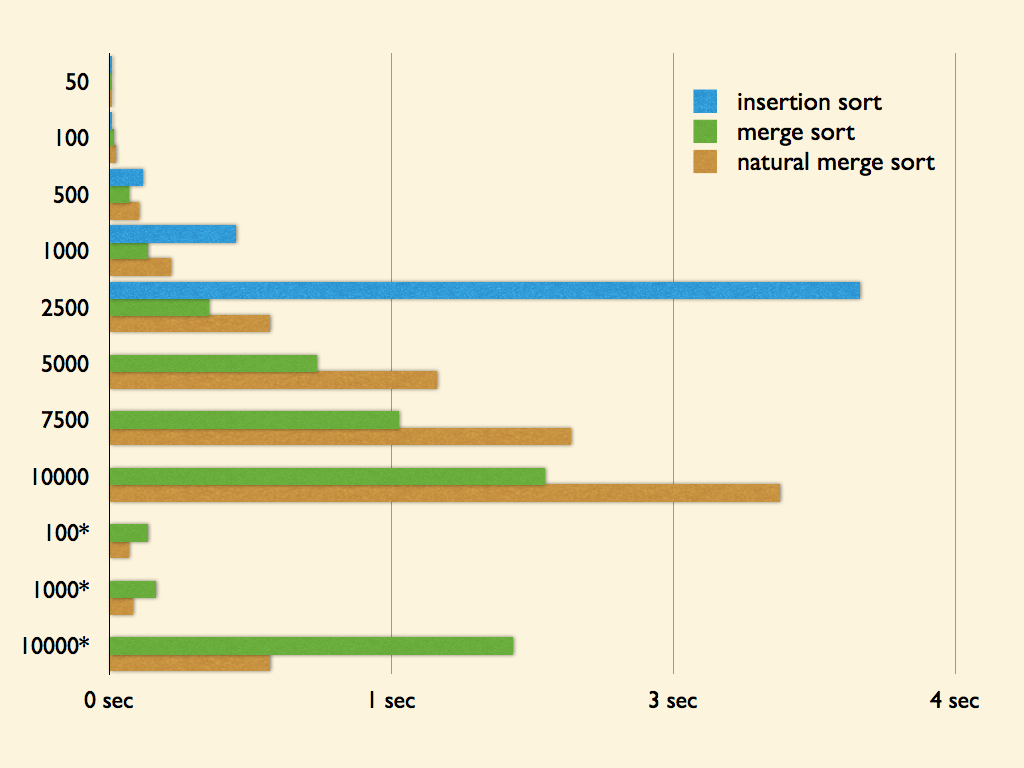 在 [淺談 merge sort](https://blog.kuoe0.tw/posts/2013/03/06/sort-about-merge-sort/) 的介紹中有一個測試實驗，比較不同資料數量下 Natural Merge Sort 和 傳統 Merge Sort 的執行時間 ![](https://raw.githubusercontent.com/KuoE0/blog-assets/master/content-photos/2013-03-06-sort-about-merge-sort-1.jpg) 測試資料皆為 100 組，單位為秒 (second)， 有星號的測試資料表示數列本身是**由多組有序數列組成** 可以觀察在一般的資料底下 Natural Merge Sort 並不一定比傳統 Merge Sort 快, 反而花的時間比較多 但在經過設計，有較多有序數列的資料底下，Natural Merge Sort 的效能就有明顯得提升 ## 前人進度 :::danger put some reference of previous work restate previous work point out problems ::: * 嘗試使用硬體提供的 clz 指令來改寫，但 mergesort 當中 clz 運算的次數很小, 所以沒有效能沒有提升很多 * 利用 __builtin_clz 指令, 及減少些微執行時間 ![](https://i.imgur.com/jymCAYb.png) * 最耗效能的部分在 merge，因此可以先偵測數字順序連續小於的區塊，減少 memcpy 的次數 ```c int conti_times_right = 0, conti_times_left = 0; while (left + conti_times_left < left_bound && right + conti_times_right < right_bound) { if (cmp(((char*) source) + size * (right + conti_times_right), ((char*) source) + size * (left + conti_times_left)) < 0) { //cmp() means? //A: user-defined comparasion function if (conti_times_left) { memcpy(((char*) target) + size * target_index, ((char*) source) + size * left, size * conti_times_left); left += conti_times_left; target_index += conti_times_left; conti_times_left = 0; } conti_times_right++; } else { if (conti_times_right) { memcpy(((char*) target) + size * target_index, ((char*) source) + size * right, size * conti_times_right); right += conti_times_right; target_index += conti_times_right; conti_times_right = 0; } conti_times_left++; } } if (conti_times_left) { memcpy(((char*) target) + size * target_index, ((char*) source) + size * left, size * conti_times_left); left += conti_times_left; target_index += conti_times_left; } else if (conti_times_right) { memcpy(((char*) target) + size * target_index, ((char*) source) + size * right, size*conti_times_right); right += conti_times_right; target_index += conti_times_right; } ``` 利用 conti_times_left, conti_times_right 來紀錄遞增數列的長度, 直到不再遞增, 再做 memcpy, 如此可以大大減少 memcpy 的次數 * Inline cmp 減少 overhead * 使用 branch predictor 的概念，先不判斷而是先作如果式子成立的結果，再來判斷如果式子不成立的結果 override (這部分還沒加入 natural mergesort) * 改變測試資料的型態，分別測試 (random, sorted, nearly sorted, reversed) * 兩篇參考文章 * 先分幾個 block, 分別排序好再 merge (與 natural mergesort 的不同: 此篇是隨機分 block, natural mergesort 是依照遞減情況分 block) * Nvidia 怎麼在 GPU 上加速 * [Github](https://github.com/petermouse/natural-mergesort) * calculate.c: 計算平均執行時間 * gen_testcase.c: 生成資料 * main.c: 輸出 ans.txt, runtime.txt * natural-mergesort.c * natural-mergesort_change.c ## Eliminating Branches with Prediction :::danger observe, assume, experiment design make an assumption, design experiment to verify it select representive measurement: ex: micro-benchmark ::: ## Introduction to branch prediction ![](https://i.imgur.com/dbSmQV0.png) Branches 會造成 pipeline 的困難, 當處理器抓到 branch 指令, 就會去抓下一步的指令, 但下一步有兩種可能, 處理器就會等待 branch 指令執行完再抓取下一步的指令, 這樣會造成 pipeline 中止。 而現代處理器會避免等待 branch 執行完再去抓取下一步指令, 因此會試圖預測下一步, 提早抓取預測的指令。當預測錯誤, 處理器就會丟棄該指令, 重新執行正確的指令。 For example, ``` int SumArray(int[] array) { if (array == null) throw new ArgumentNullException("array"); int sum=0; for(int i=0; i<array.Length; i++) sum += array[i]; return sum; } ``` 在這個例子中, (array == null) 和 (i<array.Length) 這兩個 branch, 前者當輸入錯誤時執行, 所以執行機會很小, 後者執行頻繁, 所以是很好預測的例子。 然而相對 branch 較少的情況, 若出現較多 branch, 處理器勢必更能預測出正確的下一步指令, 因此接下來我們嘗試減少 mergesort 裡 branch 的數量 ## eliminate branches orig code ```clike= while (left < left_bound && right < right_bound) { if (cmp(((char*) source) + size * right, ((char*) source) + size * left) < 0) { /* right is smaller */ memcpy(((char*) target) + size * target_index, ((char*) source) + size * right, size); ++right; } else { memcpy(((char*) target) + size * target_index, ((char*) source) + size * left, size); ++left; } ++target_index; } ``` 從以上程式碼, 我們可以看出來 branch 的其中一支是當右邊的值小於左邊的值的情況, 而另一支則相反, 因為兩者發生的機率從資料來看是剛好各 50%, 也就是預測錯誤的機會也是 50%, 因此我們嘗試減少 branch opt code ```clike= while (left < left_bound && right < right_bound) { char* v1 = ((char*) source) + size * right; char* v2 = ((char*) source) + size * left; int take = cmp(v1, v2) < 0; char* v = take ? v1 : v2; memcpy(((char*) target) + size * target_index, v, size); right = take ? right + 1 : right; left = take ? left : left + 1; ++ target_index; } ``` testcase: random, 100 numbers, range from 1~5000 ``` Performance counter stats for './natural-mergesort' (1000 runs): 0.623910 task-clock (msec) # 0.566 CPUs utilized ( +- 1.61% ) 1 context-switches # 0.827 K/sec ( +- 5.61% ) 0 cpu-migrations # 0.005 K/sec ( +- 57.68% ) 53 page-faults # 0.086 M/sec ( +- 0.06% ) 87,6290 cycles # 1.405 GHz ( +- 0.43% ) 87,0591 instructions # 0.99 insn per cycle ( +- 0.05% ) 17,2126 branches # 275.882 M/sec ( +- 0.04% ) 6800 branch-misses # 3.95% of all branches ( +- 0.26% ) 0.001103096 seconds time elapsed ( +- 5.59% ) ``` ``` Performance counter stats for './natural-mergesort_opt' (1000 runs): 0.524626 task-clock (msec) # 0.596 CPUs utilized ( +- 1.03% ) 0 context-switches # 0.810 K/sec ( +- 6.43% ) 0 cpu-migrations # 0.008 K/sec ( +- 49.92% ) 54 page-faults # 0.102 M/sec ( +- 0.05% ) 87,4084 cycles # 1.666 GHz ( +- 0.40% ) 87,6883 instructions # 1.00 insn per cycle ( +- 0.05% ) 17,3504 branches # 330.719 M/sec ( +- 0.04% ) 6704 branch-misses # 3.86% of all branches ( +- 0.24% ) 0.000880129 seconds time elapsed ( +- 1.56% ) ``` ![](https://i.imgur.com/QALhbsL.png) testcase: sorted, 100 numbers, range from 1~5000 ![](https://i.imgur.com/vr0yaKJ.png) testcase: nearly-sorted, 100 numbers, range from 1~5000 ![](https://i.imgur.com/R2wEvXY.png) testcase: reversed, 100 numbers, range from 1~5000 ![](https://i.imgur.com/NXupMVc.png) 實驗結果呈現的是, 效能沒有明顯提昇, 所以我發現去掉 if, else, 用其他判斷式, 如 C ? A : B, 並沒有降低在 branch 上消耗的 cost 在預測錯誤的情況下, 原始的程式碼是先抓取到錯誤的指令, 直到 branch 指令結束才發現預測錯誤, 丟棄原本執行的結果, 再重新執行。 而更新的程式碼是直接執行某一個 branch, 當發現預測錯誤再跳回執行另一個 branch, 所以其實是一樣的。 回頭看原始程式碼, 可以知道 branch 預測成本在於資料 random 分佈的情況, 預測準確度只有 50%, 但如果是 sorted 或 reversed 的資料, 因會傾向執行某一分支, 所以預測也會較準確。 ## Timsort 參考 Timsort，思考混合兩種以上 stable sorting algorithm 的機會 * 結合了 merge sort 和 insertion sort * 關鍵特性: 利用數據中的某些共同特性(已排序) * 方法概述 * 先將 input array 切割成許多個 sub-arrays (稱為 runs) * 利用 Insertion sort 排序各個 runs * 將排序好的 runs 利用 merge sort 合併 ### Algorithm * Step 1. Splitting input into Runs * 將 base address 設為 input array 起始 * 從目前的位置開始探訪， 尋找有序數列 (run) * 當找到的 run 長度小於 minrun 使用 insertion sort 持續將接下來的元素加入該 run 直到其長度滿足 minrun ![](https://www.infopulse.com/wp-content/uploads/2015/08/timsort-algorythm-2nd-screenshot.png) * Step 2. Merge * 結束上個步驟後，會有許多不同的 runs * 假設 input data 是 random 的，每個 run 的長度會接近於 minrun * 而當 input data 是偏向 sorted 的， run 的長度會遠超過 minrun * merge 的條件 * 當Timsort算法找到一個run時， 會將該run在數列中的起始位置和長度放入 stack 然後根據先前放入 stack 中的run决定是否合併 * 以下圖為例 X, Y, Z 分別是三個 run 的長度 當不滿足下列兩狀況時， X, Y 會被合併 (1) X>Y+Z (2) Y>Z ![](https://www.infopulse.com/wp-content/uploads/2015/08/timsort-algorythm-3rd-screenshot.png) * merge 方法 * 宣告一個臨時儲存空間，來合併兩個連續的 runs * 先將較小的 run 複製到這個臨時儲存空間 * 用原先儲存這兩個 runs 的空間来儲存合併後的 run ![](https://www.infopulse.com/wp-content/uploads/2015/08/timsort-algorythm-4th-screenshot.png) ## 參考資料 [淺談 merge sort](https://blog.kuoe0.tw/posts/2013/03/06/sort-about-merge-sort/) [Branch elimination](http://cellperformance.beyond3d.com/articles/2006/04/benefits-to-branch-elimination.html) [Fast and slow if-statements](http://igoro.com/archive/fast-and-slow-if-statements-branch-prediction-in-modern-processors/) [TIMSORT SORTING ALGORITHM](https://www.infopulse.com/blog/timsort-sorting-algorithm/)