2018q1 Homework1 (作業區)

2018q1 Homework1 (作業區) ====================== contributed by <`workat60474`> ### Reviewed by `rex662624` * 記得在 Hackmd 加上 “contributed by” * 問題回答的最後一題，有說到可以分析名字中哪個部分重複最少，但這將會使worst case非常的耗時，可能要把first name、last name等等都分析過才知道哪個部分最少重複。 * Hash 中 Collision 用到的不是這次作業較常見的 Chaining 而是 Open addressing ，因此也可以更詳細解釋讓大家了解，或是跟 Chaining 做效能上的比較。 ----- * 系統環境架構 * Cache * 將Cache的特性應用在程式上 * 實驗1.減小 size of entry * 實驗2 利用hash來加速 * 實驗3 利用Binary search tree 來加速系統環境 ------ Ubuntu 16.04.2 :::danger 請更新 Ubuntu Linux 到 17.04 後的版本，否則後續的作業可能會無法正確安裝環境 :notes: jserv ::: Linux version 4.8.0-36-generic gcc version 5.4.0 20160609 (Ubuntu 5.4.0-6ubuntu1~16.04.4) * Architecture: x86_64 * CPU 作業模式： 32-bit, 64-bit * Byte Order: Little Endian * CPU(s): 4 * On-line CPU(s) list: 0-3 * 每核心執行緒數：2 * 每通訊端核心數：2 * Socket(s): 1 * NUMA 節點： 1 * 供應商識別號： GenuineIntel * CPU 家族： 6 * 型號： 61 * Model name: Intel(R) Core(TM) i5-5257U CPU @ 2.70GHz * 製程： 4 * CPU MHz： 1008.544 * CPU max MHz: 3100.0000 * CPU min MHz: 500.0000 * BogoMIPS: 5400.35 * 虛擬： VT-x * L1d 快取： 32K * L1i 快取： 32K * L2 快取： 256K * L3 快取： 3072K * NUMA node0 CPU(s): 0-3 ![](https://i.imgur.com/LsrOa9P.png) ## Cache 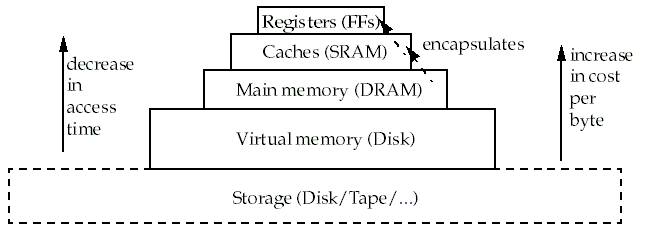因為不同的記憶體技術其存取速度和價錢上的差異，現代電腦架構利用各自的優點來建構階層式記憶體( Memory hierarchy)，在此架構中，越是靠近cpu的記憶體其存取速度越快，但價格也越高，相反地，越是在下面階層的記憶體，存取速度較慢，價格也較為便宜，如下圖所示。 ![「memory hierarchy」的圖片搜尋結果](https://m.eet.com/images/eetimes/2017/01/1331205/Besang01.png) 而最接近CPU的記憶體稱為Cache(快取)，最下層則為Disk，介於Cache和Disk之間的稱為Main memory。 ![「memory hierarchy」的圖片搜尋結果](http://ece-research.unm.edu/jimp/611/slides/chap5_1-1.gif) ## 將Cache的特性應用在程式上 **Locality:** 首先，由於程式在一小段時間只會存取一小部分的address space，這樣的行為稱為**locality(區域性)**，locality可分為兩種不同的類型 1. spatial locality (空間區域性)：意指如果一個entry被存取到，那麼他的位址附近的entry也會很快被存取到。 2. temperal locality (時間區域性)：意指如果一個entry被存取到，那麼它很快地會再次被存取到。 **Cache miss**: cache miss:當資料無法在快取記憶體中取得即稱為cache miss，cache misses可以分成以下3種種類 1. compulsory misses(強迫性失誤）:當這個區塊從未被使用過，那麼在它第一次被讀取的時候，此記憶體區塊必定不存在於快取中，這種情況下第一次存取此區塊就會發生失誤。 2. capacity misses（容量性失誤）:程式在執行時，若快取記憶體的容量不足以包含所有該程式需要讀取的區塊，就會發生快取失誤，而其中，capacity misses發生的原因在於，cache block不斷的被置換，而短暫時間後又被重新置換。 3. conflict misses（衝突性失誤）:在set-associative cache 中或者direct mapping cache中，當多個block競爭同一個working set，但是同一份working set不能同時出現在不同的block中。 confict misses只會發生在 direct mapping 或者 set-associative cache中，在fully associative的快取中是不會發生的。熟悉了以上幾點，開始來探討如何寫出cache friendly code？先從簡單的矩陣乘法看起： ![](https://i.imgur.com/3cNpb38.png) 並且假設 * Matrix element為double type (佔8個byte) * 矩陣為 n*n大小 * 一個cache block 佔 32bytes (4個double) * Cache size C遠小於n 如果我們採用非常基本的矩陣相乘程式碼 ``` for (i=0;i<n;i++) for(j=0;j<n;j++) for(k=0;k<n;k++) c[i][j]+=a[i][k]*b[k][j]; ``` 那麼在第一個iteration中（$c[0][0]=\sum_{i=0}^{n}a[0][i]*b[i][0]$) ![](https://i.imgur.com/jOJLTZd.png) (圖中,紅色部分的entry代表發生 cache miss 的entry,而淡黃色部分的entry，因為先前發生了cache miss而一同被置換進cache的部分，代表cache hit。) 會產生的 cache misses次數為： $\frac{n}{4}+n＝\frac{5}{4}n$ * 其中的 $\frac{n}{4}$ 是因為矩陣A的 $Row 0$ 由於起初不存在於 cache 中，會發生 cache miss，因為電腦架構是row-major，所以單就 $Row 0$ 共會發生 $\frac{n}{4}$次cache misses。 * 而 $n$ 則是因為，對矩陣B來說，因為要 access B的$Col0$中的所有element，而在每次的 access，而又因為row-major的關係，除了會被使用的$b[j][0]$這個element，其他被一起置換進來的如 $b[j][1], b[j][2] ...b[j][n]$, 都不會被用到，而當要access B的$b[j+1][0]$時又會再度發生一次cache misses , 這導致了一共會發生 $n$ 次的cache misses。因為矩陣具有$n^{2}$個entries，每次發生 $\frac{5}{4}n$ 次cache misses,一共會發生$n^{2}*\frac{5}{4}n=\frac{5}{4}n^{3}$ 次cache misses。如何優化？考慮block matrix 乘法 ![](https://i.imgur.com/EtXbnw9.png) 想法非常簡單，與其一次計算C的一個row，不如一次計算C中的一個block(如圖中的橘色部份)，要能夠計算C中的block，會需要矩陣A和矩陣B的淡黃色部分，這正好是一個cache block能夠放進的資料大小！在一個iteration中，cache miss的次數大幅減少了！不僅如此，當我們考慮計算下一個C中的block時 ![](https://i.imgur.com/7vTVNsb.png) 只需要透過重新放置B的下一個block就可以了。不過，假設block的size為$B^2$個double，在挑選block的size時，需要注意的是cache至少要能夠存放3個block的大小，也就是A,B,C正在計算的3個block。 $=> 3B^{2}<<C$ 而每次計算C中的一個block會有 $（\frac{B}{4}*B）*\frac{2n}{B}=\frac{B^{2}}{4}*\frac{2n}{B}=\frac{nB}{2}$次cache misses 而一共需要計算$(\frac{n}{B})^{2}$個blocks 所以透過block來進行乘法的想法，總共cache miss的次數為： $\frac{n^{3}}{2B}$ 和原本的$\frac{5n^{3}}{4}$次cache misses比較起來是不是快了不少呢？！結論: 1. 要對code做cache最佳化是一件“platform specific"的任務。（依據cache size,line size,關聯度等數值有緊密關聯） 2. 盡可能保持working set的最小化。(因為temporal locality) 3. 選用small stride(因為spatial locality) ## 實驗1 減小 size of entry 想法非常簡單，就像作業解說影片裡面提到的，由於原本的 entry size 為 136 bytes,但是我們只透過比對last name欄位來進行比對，若把entry size縮小，並且另外定義addi_entry來存放其他的欄位，就能降低entry size到36 bytes。 phonebook_orig.h ``` /* original version */ typedef struct __PHONE_BOOK_ENTRY { char lastName[MAX_LAST_NAME_SIZE]; char firstName[16]; char email[16]; char phone[10]; char cell[10]; char addr1[16]; char addr2[16]; char city[16]; char state[2]; char zip[5]; struct __PHONE_BOOK_ENTRY *pNext; } entry; ``` ``` size of entry : 136 bytes execution time of append() : 0.049628 sec execution time of findName() : 0.005275 sec ``` Cache miss 在orig的版本高達93% ``` Performance counter stats for './phonebook_orig' (100 runs): 3,415,271 cache-misses # 93.074 % of all cache refs ( +- 0.04% ) 3,669,415 cache-references ( +- 0.16% ) 261,936,549 instructions # 1.43 insn per cycle ( +- 0.02% ) 183,523,356 cycles ( +- 0.34% ) 0.060063780 seconds time elapsed ( +- 0.39% ) ``` phonebook_opt.h ``` typedef struct addi_entry{ char firstName[16] ; char email[16]; char phone[10]; char cell[10]; char addr1[16]; char addr2[16]; char city[16]; char stat[2]; char zip[5]; }detail_entry; typedef struct __PHONE_BOOK_ENTRY { char lastName[MAX_LAST_NAME_SIZE]; // char firstName[16]; //char email[16]; //char phone[10]; //char cell[10]; //char addr1[16]; //char addr2[16]; //char city[16]; //char state[2]; //char zip[5]; detail_entry *detail ; struct __PHONE_BOOK_ENTRY *pNext; } entry; ``` ``` size of entry : 32 bytes execution time of append() : 0.035499 sec execution time of findName() : 0.002242 sec ``` Cache-misses在opt(降低了entry size)的版本為72% ``` 1,190,529 cache-misses # 72.689 % of all cache refs ( +- 0.08% ) 1,637,849 cache-references ( +- 0.32% ) 244,368,274 instructions # 1.98 insn per cycle ( +- 0.02% ) 123,133,474 cycles ( +- 0.35% ) 0.040567132 seconds time elapsed ( +- 0.47% ) ``` ![](https://i.imgur.com/acoBukq.png) :::danger 你要如何解釋上圖呈現的時間落差？請量化分析。 :notes: jserv ::: **為何cache miss降低了？** 由於我的 L1d Cache之大小為32kb,因此在orig的版本中，因為entry的大小136bytes，L1d cache能夠存放的entry數目為(32 * 1024)/136=240筆struct資料,而之後縮小了entry大小至36bytes，L1d cache能夠存放的資料數目為(32* 1024)/36=910筆，能夠存放的資料增加了，cpu有更多次可以在cache裡面找到所需的資料，這是造成cache miss降低的原因。 **為何append和findname的時間降低了？** 當發生cache miss的時候，cpu會 1.stall cpu ,凍結暫存器裡面的資料。 2.使用分離的cache controller 來處理cache miss，並透過置換演算法（如LRU,FIFO)，選出要放置資料的cache，並將資料從main memory載入到cache。 3.一旦資料載入cache，我們將從造成cache miss的cycle重新開始執行。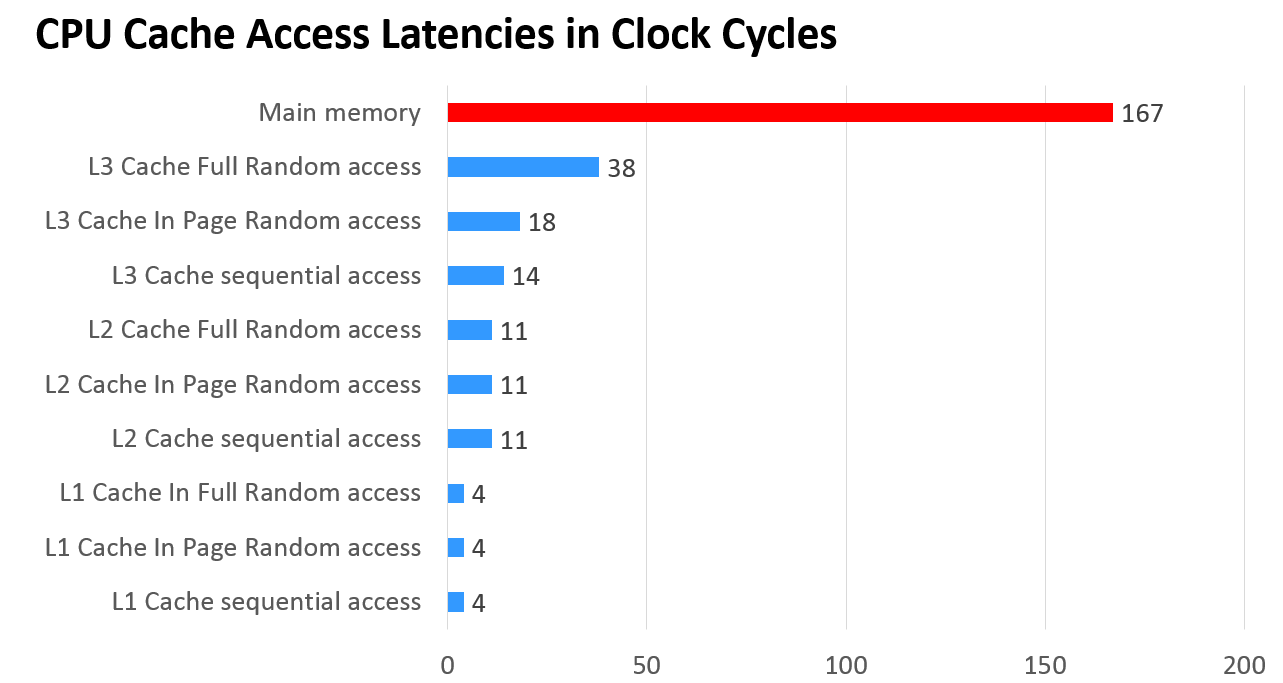在Memory hierarchy的架構下，不同level之記憶體之存取速度不同，在步驟2中cpu到cache的下一層中去尋找資料，所需的access time（或說access latencies) 比起cache差異慎大（見下圖） ![latency](http://cenalulu.github.io/images/linux/cache_line/latency.png) 透過降低cache miss rate，就能減少存取main memory的次數，也就能減少miss penalty的時間，這是append和findname的時間降低的原因。 ———————————————————————————————————————————— ＊遇到的小問題：我在減少entry大小之後，使用make plot所畫出來的圖卻和perf驗證的不同, 在圖上append和findname的時間都沒有降低！後來仔細看了一下問題出在一開始的phonebook_opt.h裡面的 ``` //#define opt 1 ``` 是被註解的，這導致了phonebook資料夾下根本不會生成opt.txt，因為在main.c裡面有這麼一段 ``` #ifdef OPT #define OUT_FILE "opt.txt" #else #define OUT_FILE "orig.txt" #endif ``` 這導致了它只會生成orig.txt，所以只要把phonebook_opt.h裡面的 ``` //#define opt 1 ``` 把註解拿掉改成 ``` #define opt 1 ``` 就能成功生成opt.txt,如此一來make plot所畫出的圖才會符合perf的結果。 ## 實驗2 利用hash來加速設定hash_table size為32768 * Based on BKDR hash funtion 1,756,771 cache-misses # 78.296 % of all cache refs ( +- 0.11% ) 2,243,769 cache-references ( +- 0.38% ) 272,646,864 instructions # 1.32 insn per cycle ( +- 0.02% ) 205,835,785 cycles ( +- 0.34% ) 0.068301698 seconds time elapsed ( +- 0.35% ) ``` size of entry : 24 bytes execution time of append() : 0.041564 sec execution time of findName() : 0.000000 sec ``` ![](https://i.imgur.com/QxrBhHB.png) 如圖，可以看出append的時間增加，findName的時間大幅降低，Cache misses的比例為78%。 WHY? * findName的時間大幅降低是可以想見的，由於先前的version-1採取linked-list來存放資料，在linked-list中找到特定欄位所需之time complexity為$O(n)$,而hash table中存取特定欄位，考慮collision和Probing的發生，其complexity為$O(1)(amortized)$ ，比對的時間大幅減少（為constant time)。 * append所花的時間增加：利用perf發現花在計算hash_index的時間為hot spot，append的時間甚至少他的一半，下面附上其程式碼。 * 利用perf查看overhead發現許多時間花費在計算hash index上。 ``` Samples: 308 of event 'cpu-clock', Event count (approx.): 77000000 Overhead Command Shared Object Symbol 33.12% phonebook_hash phonebook_hash [.] release_hash_table 10.39% phonebook_hash phonebook_hash [.] main 8.12% phonebook_hash libc-2.23.so [.] _int_malloc 6.49% phonebook_hash libc-2.23.so [.] free 5.84% phonebook_hash phonebook_hash [.] bkdr_hash 5.52% phonebook_hash libc-2.23.so [.] _IO_fgets ``` ``` unsigned int bkdr_hash(char *str) { unsigned seed = 127; unsigned hash=0; while(*str) hash = hash*seed+(*str++); return hash % HASH_TABLE_SIZE; } ``` **如何降低cache misses?** 起初我將hash table的size設為32768，嘗試改變hash table size的大小來觀察對於cache misses的影響 1. hash table size = 42737 ``` 1,463,096 cache-misses # 64.478 % of all cache refs ( +- 1.07% ) (25.49%) 2,269,125 cache-references ( +- 1.28% ) (26.34%) 274,351,833 instructions # 1.18 insn per cycle ( +- 1.11% ) (25.79%) 233,485,406 cycles ( +- 0.36% ) (25.32%) 0.081729874 seconds time elapsed ( +- 0.37% ) ``` cache misses 確實有下降，我後續嘗試了不同的數值: | hash table size | cache misses | cache reference|append time| | -------- | -------- | -------- |-------| | 10000|3505174| 5186209|0.047050sec| | 20000|1506168|2101795|0.050490sec | 30000|1450283|2191374|0.050414sec | 40000|1514148|2244696|0.045116sec | 50000|1495635|2293420|0.049817sec | 60000|1543214|2381301|0.046142sec | 70000|1608300|2441266|0.047791sec | 80000|1418144|2316503|0.046550sec | 90000|1578929|2424464|0.054449sec | 100000|1327630|2431227|0.047374sec | 110000|1335383|2421136|0.047381sec | 120000|1401031|2495336|0.051134sec | 130000|1625883|2564941|0.046979sec | 140000|1370780|2283537|0.051699sec | 160000|1384432|2321349|0.046852sec Q:為什麼hash table size 在10000以下，會造成cache misses上升？ A:由於這次實驗採open addressing ，一旦發生collision，得透過Probing到其他的buckets去尋找空的slot來存放資料。考慮在hash table size遠大於cache size的前提下(本例）：當hash table size減少時會造成load factor 的上升，代表整個hash table已經被用以存放資料的比例越高，也就是說空的slot數目較少，這也造成需要更多次的Probing來尋找空的slot，違反locality of reference，Cache misses也隨之提高。換言之，collision的次數和cache miss的次數為正相關。反之若是hash table size小於cache size，那麼整個 hash table 的資料都能夠存放在cache中，並不會有因為拜訪hash table中某個slot的資料造成cache miss的情況。 cache misses在hash table size大於20000以後，並無明顯差異，append()time也無明顯差異。 ## 實驗3 利用Binary search tree 來加速參考了[Ryan Wang同學的作法](https://hackmd.io/s/Sk-qaWiYl#) 利用Sorted Linked List to Balanced BST 作法請參考：https://www.geeksforgeeks.org/sorted-linked-list-to-balanced-bst/ ``` example: Input: Linked List 1->2->3 Output: A Balanced BST 2 / \ 1 3 Input: Linked List 1->2->3->4->5->6->7 Output: A Balanced BST 4 / \ 2 6 / \ / \ 1 3 4 7 ``` 探討其操作的複雜度使用Binary search，insert/search/deletion之time-complexity取決於find的時間複雜度，也就是樹的高度。因此對一個具有$N$個elements的binary search tree來說： | $time-complexity$ | Best-case | average-case |worst-case | | -------- | -------- | -------- | --------| | insertion| $O(logN)$| $O(logN)$ |$O(N)$| | find-specify-element| $O(logN)$| $O(logN)$ |$O(N)$| 實驗結果： ``` size of entry : 32 bytes execution time of append() : 0.041623 sec execution time of findName() : 0.000000 sec 1,589,273 cache-misses # 81.076 % of all cache refs ( +- 0.09% ) 1,960,233 cache-references ( +- 0.24% ) 343,192,582 instructions # 1.53 insn per cycle ( +- 0.01% ) 224,503,303 cycles ( +- 0.18% ) 0.073416944 seconds time elapsed ( +- 0.21% ) ``` ![](https://i.imgur.com/UGyLSpR.png) | | orig | reduece-entry-size | Hash | B.S.T| | -------- | -------- | -------| -------- | -------- | | append-time| 0.052535 sec | 0.052535 sec | 0.062574 sec | 0.036677 sec| | findName-time | 0.005210 sec | 0.001943 sec |0.000000 sec| 0.000000 sec| | cache-miss | 3,415,271 | 1,190,529 |1,463,096|1,589,273 | |instruction-count | 261,936,549 |244,368,274 |274,351,833| 343,192,582| * Cache-misses增加的原因：在binary-search-tree中，由於樹狀結構，每次發生cache-misses時，cache-controller將main memory中的資料搬到cache，因為Tree structure無法如同array或者linked-list的排列方式，無法發揮cache中的locality of reference的效益。 * findName比起reduce_entry_size時間低的原因： B.S.T search的複雜度為$O(logN)$~$O(N)$，而由於原本的資料是已經排序過的，如此建成的B.S.T不會為worst-case，考慮average-case的話： $N$$\approx$$400000$ linked-list search的time-complexity $O(N)$ 而B.S.T average的search time-complexity $O(logN)$ $\frac{N}{logN}\approx$ $21494.2357731$ 倍的時間差距 * append時間比起reduce_entry_size時間高的原因：由於B.S.T利用insertion來建樹，所花的time-complexity為$O(NlogN)$，相較於link-list建立的time-complexity為$O({N}^2)$， $\frac{{N}^2}{NlogN}\approx$ $18$ * 為什麼時間和複雜度所計算出的比例不同？ ## 問題回答補充：本例選用的 dataset (也就是輸入電話簿的姓名) 是否存在問題？ * 有代表性嗎？跟真實英文姓氏差異大嗎？ ANS:差異慎大，許多姓名不存在於現實世界中，不僅如此，只透過last name來進行批配也不夠嚴謹，應該考慮last name重複的話，再對於姓名的其他部份（eg. middle name,first name) 再進行比較。 * 資料難道「數大就是美」嗎？ ANS:與其說數大便是美，不如說能夠使用適當且有效率的資料結構和演算法，來降低對資料操作的複雜度，並了解資料的特性，搭配電腦硬體的適應方式，寫出適當且有效率的程式碼。 * 如果我們要建立符合真實電話簿情境的輸入，該怎麼作？ ANS: 考慮到姓名中，可能重複的部份，如果能夠先對資料整體做一次分析，判斷中先利用名子的哪個部份做批配，發生重複的機率最低，再搭配適當資料結構和演算法來撰寫存放資料和查找的方法。 ## 參考資料 * [关于CPU Cache -- 程序猿需要知道的那些事](http://cenalulu.github.io/linux/all-about-cpu-cache/) * [淺談memory cache ](http://opass.logdown.com/posts/249025-discussion-on-memory-cache) * https://zh.wikipedia.org/wiki/%E5%93%88%E5%B8%8C%E8%A1%A8#.E8.BD.BD.E8.8D.B7.E5.9B.A0.E5.AD.90