# 2017-11-17 課堂練習

## 學習方式

搭配 [15-213/18-213/15-513: Intro to Computer Systems](http://www.cs.cmu.edu/~213/schedule.html) (目前 2017 Fall) 的投影片和錄影 (YouTube 可開字幕)
:::info
1. 以下頁面以簡體中文《深入理解計算機系統》為主
2. 下方隨堂練習請在檢討後，於 11 月 25 日前，將完整作答和討論的共筆發信到 `<[e-mail]>`，標題是 `[sysprog] 你的姓名` (中間有空格)
:::

## 數值系統

:::success
隨堂練習
- [x] 2.58: 撰寫函式 `is_little_endian`，在 Little endian 機器上返回 `1`，反之返回 `0`，應能再任意機器上，無論幾位元的架構都適用 (==Page 88==)
- [x] 2.66: 撰寫函式 `leftmost_one`，產生得以找出數值 x 最高位 `1` 的位元遮罩 (==Page 90==)
- [x] 2.92: 撰寫函式 `float_negate`，給定浮點數 `f`，回傳 `-f`，倘若 `f` 是 $NaN$，直接回傳 `f`。輸入數值範圍為有效的 2^32^ 個數值 (==Page 96==)
:::
### 2.58
* is_little_endian

#include <stdio.h>
#include <stdlib.h>
int main() {
    int char_var = 1;
    unsigned char *test = (unsigned char*) &char_var;
    
    printf("%d, is little endin = %d\n", test[0], test[0] == 1);
    return 0;
} 

這主要是利用了 int 的 4bytes 大小以及 char 的 1byte 大小差異來分辨位元之間的排列方法。

根據[參考資料](https://stackoverflow.com/questions/12791864/c-program-to-check-little-vs-big-endian)，電腦若是 little_endin，其記憶體配置如下：

   higher memory
      ----->
+----+----+----+----+
|0x01|0x00|0x00|0x00|
+----+----+----+----+
char_var
|
test

可以發現 test[0] 會是 1。

另一方面，若是 big_endin：

   higher memory
      ----->
+----+----+----+----+
|0x00|0x00|0x00|0x01|
+----+----+----+----+
char_var
|
test

test[0] 就便成了 0。

### 2.66
* leftmost_one

int leftmost(unsigned x) {
    x |= x >> 1;
    x |= x >> 2;
    x |= x >> 4;
    x |= x >> 8;
    x |= x >> 16;
    return x ^ (x >> 1);
}                          

後來觀察了一下它的數值變化過程，以 $10_{10} = 1010_2$ 為例：
清楚發現到這個 function 的前面右移部份負責將最高為一的位元後的所有位元填滿，接著結果本身與右移一格的結果進行 ```XOR``` 即可獲得最高位元的遮罩。

同樣方法，我們亦可以取出最低位元的遮罩，僅須換個方向：
* rightmost_one

int leftmost(unsigned x) {
    x |= x << 1;
    x |= x << 2;
    x |= x << 4;
    x |= x << 8;
    x |= x << 16;
    return x ^ (x << 1);
}                          


### 2.92
* float_negate
根據[教學](https://www3.ntu.edu.sg/home/ehchua/programming/java/datarepresentation.html)所示，我們知道了 float 的單精度二進位表示方式：

並且同時也知道了 ==$NaN$== 以及 ==$\pm\infty$== 的表示方法：
$NaN$: Exponent 段全為一，且 Fractction 段非零。
$\pm\infty$: Exponent 段全為一， Fraction 段也是零，並依照 S 段決定正負。

因此可以寫出以下程式：

typedef unsigned float_bits;

float_bits float_negate(float_bits f) {
    unsigned sign = f >> 31;
    unsigned exp  = f >> 23 & 0xFF;
    unsigned frac = f & 0x7FFFFF;
    
    // NaN
    if (exp == 0xFF && frac != 0) {
        return f
    }
    
    return (sign << 31) | (f & 0x7FFFFFFF);
}

但有趣的是，上面的參考資料時發現 float 當中亦存在 $\pm0$，如下圖：

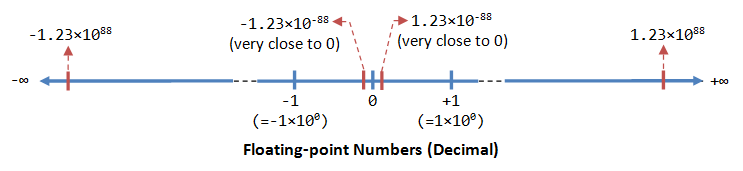
雖然浮點數的表示方法使用 $(-1)^s \times 1.frac \times 10^{exp}$ 的科學記號表示，對於小數有很高的表示能力，但由於表示用的科學記號預期會帶有 1 在最前面，因此就是沒辦法完全的表現 0 ，這部份只能透過 ==趨近== 的方式由正負兩個方向趨近，因此才會出現 $+0$ 以及 $-0$。

## 計算機組織與結構

:::success
隨堂練習
- [x] 4.47: 以 C 語言指標改寫原本使用陣列表示法的氣泡排序程式碼 (==Page 327==) / 延伸題目: [最佳化](https://en.wikipedia.org/wiki/Bubble_sort#Optimizing_bubble_sort) / [Analysis on Bubble Sort Algorithm Optimization](http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=5635119)
:::
### 4.47
一開始我不太清楚這個題目的意義，但為了符合題意我依然寫了一個程式，開始做點研究。

以下使用指標作為 bubble sort 的 index 作法：

void bubble(long *data, long count) {
    long *i, *j;
    
    for (i = data; i < data + count - 1; i ++) {
        for (j = i; i < data + count; j ++) {
            if (*j > *(j + 1)) {
                long t = *(i + 1);
                *(i + 1) = *i;
                *i = t;
            }
        }
    }
}

表面上看似沒什麼差別，這邊我們看看組合語言：

    // void bubble(long *data, long count) {
    push rbp
    mov rbp,rsp
    mov QWORD PTR [rbp-0x28],rdi
    mov QWORD PTR [rbp-0x30],rsi
    
    // for (i = data; i < data + count - 1; i ++) {
    mov rax,QWORD PTR [rbp-0x28]
    mov QWORD PTR [rbp-0x8],rax
    jmp 4005f9 <bubble(long*, long)+0x83>
    
    // for (j = i; i < data + count; j ++) {
    mov rax,QWORD PTR [rbp-0x8]
    mov QWORD PTR [rbp-0x10],rax
    jmp 4005db <bubble(long*, long)+0x65>
    
    // if (*j > *(j + 1)) {
    mov rax,QWORD PTR [rbp-0x10]
    mov rdx,QWORD PTR [rax]
    mov rax,QWORD PTR [rbp-0x10]
    add rax,0x8
    mov rax,QWORD PTR [rax]
    cmp rdx,rax
    jle 4005d6 <bubble(long*, long)+0x60>
    
    // swap, t = i, i = j, j = t
    mov rax,QWORD PTR [rbp-0x8]
    mov rax,QWORD PTR [rax+0x8]
    mov QWORD PTR [rbp-0x18],rax
    mov rax,QWORD PTR [rbp-0x8]
    lea rdx,[rax+0x8]
    mov rax,QWORD PTR [rbp-0x8]
    mov rax,QWORD PTR [rax]
    mov QWORD PTR [rdx],rax
    mov rax,QWORD PTR [rbp-0x8]
    mov rdx,QWORD PTR [rbp-0x18]
    mov QWORD PTR [rax],rdx
    
    // for (j = i; i < data + count; j ++) {
    add QWORD PTR [rbp-0x10],0x8
    mov rax,QWORD PTR [rbp-0x30]
    lea rdx,[rax*8+0x0]
    mov rax,QWORD PTR [rbp-0x28]
    add rax,rdx
    cmp rax,QWORD PTR [rbp-0x8]
    ja 400596 <bubble(long*, long)+0x20>
    
    // for (i = data; i < data + count - 1; i ++) {
    add QWORD PTR [rbp-0x8],0x8
    mov rax,QWORD PTR [rbp-0x30]
    shl rax,0x3
    lea rdx,[rax-0x8]
    mov rax,QWORD PTR [rbp-0x28]
    add rax,rdx
    cmp rax,QWORD PTR [rbp-0x8]
    ja 40058c <bubble(long*, long)+0x16>
    
    // }
    pop rbp
    ret

這邊我們對照原版的 bubble sort：

void bubble(long *data, long count) {
    int i, j;
    
    for (i = 0; i < count - 1; i ++) {
        for (j = i; j < count - 1; j ++) {
            if (data[j] > data[j + 1]) {
                long t = data[j + 1];
                data[j + 1] = data[j];
                data[j] = t;
            }
        }
    }
}

組合語言為：
為方辦觀察這裡只擷取 ```if (data[j] > data[j + 1]) {``` 以及 ```swap``` 的部份

    push rbp
    
    ...
    
    // if (data[j] > data[j + 1]) {
    mov eax,DWORD PTR [rbp-0x8]
    cdqe 
    lea rdx,[rax*8+0x0]
    mov rax,QWORD PTR [rbp-0x18]
    add rax,rdx
    mov rdx,QWORD PTR [rax]
    mov eax,DWORD PTR [rbp-0x8]
    cdqe 
    add rax,0x1
    lea rcx,[rax*8+0x0]
    mov rax,QWORD PTR [rbp-0x18]
    add rax,rcx
    mov rax,QWORD PTR [rax]
    cmp rdx,rax
    jle 40063c <bubble(long*, long)+0xc6>
    
    // swap, t = i, i = j, j = t
    mov eax,DWORD PTR [rbp-0x8]
    cdqe 
    add rax,0x1
    lea rdx,[rax*8+0x0]
    mov rax,QWORD PTR [rbp-0x18]
    add rax,rdx
    mov rax,QWORD PTR [rax]
    mov QWORD PTR [rbp-0x10],rax
    mov eax,DWORD PTR [rbp-0x8]
    cdqe 
    add rax,0x1
    lea rdx,[rax*8+0x0]
    mov rax,QWORD PTR [rbp-0x18]
    add rdx,rax
    mov eax,DWORD PTR [rbp-0x8]
    cdqe 
    lea rcx,[rax*8+0x0]
    mov rax,QWORD PTR [rbp-0x18]
    add rax,rcx
    mov rax,QWORD PTR [rax]
    mov QWORD PTR [rdx],rax
    mov eax,DWORD PTR [rbp-0x8]
    cdqe 
    lea rdx,[rax*8+0x0]
    mov rax,QWORD PTR [rbp-0x18]
    add rdx,rax
    mov rax,QWORD PTR [rbp-0x10]
    mov QWORD PTR [rdx],rax

    ...
    
    pop rbp
    ret

可以很明顯的察覺到，注意到，兩邊 swap 的部份指令數差距超過兩倍 (11/28)，並且在 if( a > b) 的判斷方面也是有著 7:15 的巨大差距。再更加仔細觀察便會發現原始版本為了實做陣列的 index 運算以及存取，多了許多 add 以及 lea 運算，並且也為了使用這個新計算出來的 index，必須多一道 mov 指令，導致比起原先僅需要兩道指令來載入到暫存器的讀取動作，至少多了兩道(index 的add以及 lea)，再計算其他流程上的影響，最終導致指令數多出一倍以上，可見即使是基本的矩陣存取方法上依然有不少陷阱阿。

:::success
隨堂練習
- [x] 6.37: 計算 `N=64` 和 `N=60` 的 cache miss rate (==Page 455==)
- [x] 6.45: 撰寫更快的轉置矩陣實作 (==Page 45==)
- [x] 6.46: 有向圖轉換為無向圖 (==Page 45==) / 參考: [Graph](http://www.csie.ntnu.edu.tw/~u91029/Graph.html), [相鄰矩陣 (Adjacency Matrix))](https://hellolynn.hpd.io/2017/09/22/%E5%AF%A6%E4%BD%9Cgraph%E8%88%87dfs%E3%80%81bfs%E8%B5%B0%E8%A8%AA/)
:::

### 6.37
題目要求在 4KB cache、16 byte cache block 的 Direct Mapping cache 狀況下計算以下程式碼中的各個 sum 在 N=60, 64 時的 cache miss rate。其中陣列 a 從0x08000000 開始儲存。

typedef int array_t[N][N];

int sumA(array_t a) {
    int i, j;
    int sum = 0;
    for (i = 0; i < N; i++)
        for (j = 0; j < N; j++) {
            sum += a[i][j];
        }    
    return sum;
}

int sumB(array_t a) {
    int i, j;
    int sum = 0;
    for (j = 0; j < N; j++)
        for (i = 0; i < N; i++) {
            sum += a[i][j];
        }
    return sum;
}

int sumC(array_t a) {
    int i, j;
    int sum = 0;
    for (j = 0; j < N; j += 2)
        for (i = 0; i < N; i += 2) {
            sum += a[i][j] + a[i + 1][j]
                    + a[i][j + 1] + a[i + 1][j + 1];
        }
    return sum;
}

* Direct Mapping Cache
雖說是 Direct Mapping Cache 但其實際上存在兩種定址方式，如[參考網站所述](http://fourier.eng.hmc.edu/e85_old/lectures/memory/node4.html)：
其存在 Continuous 以及 Interleaved 兩種映射方法，將會把兩者的數值計算出來。

根據[參考共筆](https://hackmd.io/s/H1U6NgK3Z)所整理的 cache address 組成示意圖：

我們可以計算出實際上這個 cache 包含多少 set：
$S = 4KB / (16byte \times E) = 256, E = 1$

由於 a 從 0x08000000 開始儲存，這邊根據 address 的表示法判斷總記憶體大小為 $2^{32} byte = 8GB$，這裡根據 address 組成並假設 0x080000000 之後不會存放任何程式執行時會被存取到的資料，開始分項討論：

### Continuous Mapping

| set index | tag | block offset |
| --------- | -------- | ------------ |
| 8 bits | 20 bits | 4 bits |

#### N = 60, a size = 14400 bytes($2^{13} < a_{size} < 2^{14}$)
這個大小由於並未大於 $2^{24}$ 因此整個陣列將被對應於單一個 16bytes 的cache。

##### sumA
程式碼是循序存取，因與陣列在記憶體中的實際配置方法相同順序，不難推測其基本上每四次記憶體存取就會出現一次(第一次存取)失敗，得失敗率為 ==25%==。

##### sumB
程式碼與 sumA 的差距為，sumB 為跳列存取，每次都為跳下一列的存取方式，並且由於整個 a 陣列都會對應到同一個 cache block，導致次跳列都會造成 cache miss，並且 cache block 遭到清空。
因此可得失敗率為 ==100%==。

##### sumC
此方法看似複雜，實際上是在外部迴圈部份每次都 +2，並且在內部加法時可以透過多寫些加法項來實做。
若編譯時程式所採用的 evaluation 順序為：

a[i][j];
a[i + 1][j];
a[i][j + 1];
a[i + 1][j + 1];

即原始順序，則每次存取將確實跳轉一排，導致失敗率為 ==100%==。

若編譯時其順序有經過微調：

a[i][j];
a[i][j + 1];
a[i + 1][j];
a[i + 1][j + 1];

則每兩次存取會出現一次失敗，即失敗率為 ==50%==。

#### N = 64, a size = 16384 bytes($a_{size} = 2^{14}$)
由於在 continuous 的 mapping 方式中，整個 a 陣列依然被對應在一個 cache block 當中，因此其結果也將相同。

### Interleaved Mapping

| tag | set index | block offset |
| -------- | --------- | ------------ |
| 20 bits | 8 bits | 4 bits |

#### N = 60, a size = 14400 bytes($2^{13} < a_{size} < 2^{14}$)
在 Interleaved Mapping 的狀況下 a 陣列可以被切割為 900 個 block，但實際上系統中只有 256 個 block，根據鴿籠原理，前面 132 個 block 將會對應到 4 個 a 陣列值($index = i, i + 1024, i + 2 \times 1024, i + 3 \times 1024$)，剩下的 124 個 block 則對應到三次。

##### sumA
雖然這次的 Direct Mapping 方法不同，但由於其為循序存取，失敗率與 Continuous Mapping 時相同為 ==25%==。

##### sumB
根據估算，整個 Direct Mapping 4KB Cache 可以塞下 17 行又 4 個 int，其本身雖採取跳行存取，但由於其 cache id 在 j 相同的一列當中並不是完全對齊(多了 4 個 int)的，因此存取後續行時並不會覆蓋到上一次 17 行的 cache 結果，再加上其行數為 60 並未超過 cache block 可用極限，可以完整載入一列。第一次 $[0][0] ~ [59][0]$ 雖然全部失敗但後續的 $[0][1] ~ [59][1], [0][2] ~ [59][2], [0][3] ~ [59][3]$ 皆會成功，以此計算失敗率為 ==25%==。

##### sumC
這裡使用上面 Interleaved Mapping, N=60, sumB 的相同想法來理解，雖然它一次存取兩行的各兩個元素，但我們可以注意到實際上 a[i][j + 1] 以及 a[i + 1][j + 1] 都是保證會命中的，並且 a[i][j] 以及 a[i + 1][j] 則是皆僅在每次 $j\mod4 = 0$ 時失敗(與 sumB 相同)，以此可以計算出失敗率為 2/4(j) + 0/4(j + 2) = 2 / 8 = ==25%==。

#### N = 64, a size = 16384 bytes($a_{size} = 2^{14}$)

##### sumA
由於其為正常順序存取，cache miss = ==25%==。

##### sumB
雖然存取方法與 N=60 時的 sumB 相同，但十分不幸的當 N = 64 時，其每 16 行剛好對齊整個 cache，也就是每跳 16 行便會開始覆蓋上 16 行的 cache 結果，最後導致每次讀取都會是新的 block，同時 cache 使用率也極低。失敗率為 ==100%==。

##### sumB
這個方法雖然比起 N=60 時的 sumC 同樣受到了影響，但由於其還是包含循序讀取的部份(a[i][j] -> a[i][j + 1], a[i + 1][j] -> a[i + 1][j + 1])，即使跳行讀取完全失敗，其依然有 2/4 的正確率，因此其失敗率為 ==50%==。

#### 總結
以下總結做表
* Continuous Mapping

| type\N | 60 | 64 |
| ------ | ---------- | ---------- |
| sumA | 25% | 25% |
| sumB | 100% | 100% |
| sumC | 100% / 50% | 100% / 50% |

* Interleaved Mapping

| type\N | 60 | 64 |
| ------ | --- | ---- |
| sumA | 25% | 25% |
| sumB | 25% | 100% |
| sumC | 25% | 50% |

### 6.45
由於並不是很了解題目的限制條件，這邊我參考了 [github 上的解答](https://github.com/DreamAndDead/CSAPP-3e-Solutions/blob/master/chapter6/6.45.md) 才了解一些此題的目的。

題目透過一次交換兩列的兩個元素來達到至少 50% 的 cache 命中率。其中假設 block 為 8 bytes，可以儲存 2 個 int。

for (i = 0; i <= N - 2; i += 2) {
    for (j = 0; j <= N - 2; j += 2) {
        dst[j * N + i] = src[i * N + j];
        dst[j * N + i + 1] = src[(i + 1) * N + j];
        dst[(j + 1) * N + i] = src[i * N + j + 1];
        dst[(j + 1) * N + i + 1] = src[(i + 1) * N + j + 1]; 
    }
}

因此這邊提出了改良版：

c = 4; // Cache Block Size(byte) / 4
for (i = 0; i < N - c; i += c) {
    for (j = 0; j < N - c; j += c) {
        for (n = 0; n < c; n ++) {
            for (m = 0; m < c; m ++) {
                dst[(j + m) * N + (i + n)] = src[(i + n) * N + (j + m)];
            }
        }
    }
}

if (i != N) {
    for (; i < N; i ++) {
        for (; j < N; j ++) {
            dst[j * N + i] = src[i * N + j];
        }
    }
}

其可以根據 c 所定義的一個 block 能儲存的 int 數量，以此決定要翻轉的子矩陣大小。

另外，若是在於 continuous mapping 的 cache 環境下，則必須慎重決定 n 跟 m 的順序，若是翻轉本身讀取效能較為吃重，優先建議寫成以下：

for (m = 0; m < c; m ++) {
    for (n = 0; n < c; n ++) {
        dst[(i + n) * N + (j + m)] = src[(j + m) * N + (i + n)];
    }
}

使 src 的橫列部份優先進行迭代。

同樣，若是寫入效能較為吃重，由於 cache 本身 write back 的策略，則建議先將資料完整寫入 dst 的快取後才進行換列：

for (n = 0; n < c; n ++) {
    for (m = 0; m < c; m ++) {
        dst[(i + n) * N + (j + m)] = src[(j + m) * N + (i + n)];
    }
}

### 6.46
利用與 6.45 相同的想法，依然是在運算時希望可以盡量利用到 cache，並且盡量不讓之前載入至 cache 的資料失效。

由於這次我們必須==讀取兩個元素==運算後寫入至==一個地方==，為了最大化效能表現，我們會希望這些動作都能被 cache 所包含，並且對於寫入是友善的(這邊假設是 write-back)。
首先我參考 6.45 所寫的程式碼，改寫為：

c = 4; // Cache Block Size(byte) / 4
for (i = 0; i < dim - c; i += c) {
    for (j = 0; j < dim - c; j += c) {
        for (n = 0; n < c; n ++) {
            for (m = 0; m < c; m ++) {
                G[(j + m) * dim + (i + n)] =
                    G[(i + n) * dim + (j + m)] ||
                    G[(j + m) * dim + (i + n)];
            }
        }
    }
}

if (i != dim) {
    for (; i < dim; i ++) {
        for (; j < dim; j ++) {
            G[j * dim + i] = G[i * dim + j] || G[j * dim + i];
        }
    }
}

其中改寫最為核心的部份是：

for (n = 0; n < c; n ++) {
    for (m = 0; m < c; m ++) {
        G[(j + m) * dim + (i + n)] =
            G[(i + n) * dim + (j + m)] ||
            G[(j + m) * dim + (i + n)];
    }
}

然而這段程式碼有個缺點，寫入的過程由於是跳行的操作，根據 6.37 告訴我其有可能每次都觸發 cache-miss，並且直接造成必須將 cache 中的資料寫回至原來目標，造成效能消耗。為此我再修改一下程式碼：

for (n = 0; n < c; n ++) {
    for (m = 0; m < c; m ++) {
        G[(i + n) * dim + (j + m)] =
            G[(j + m) * dim + (i + n)] ||
            G[(i + n) * dim + (j + m)];
    }
}

這份程式碼至少可以確保 G[(i + n) * dim + (j + m)] 在於讀取以及寫入上的效能，即使是 continuous mapping 的策略中依然不會變成 100% 的 cache-miss。

## 參考資料
* [C program to check little vs. big endian](https://stackoverflow.com/questions/12791864/c-program-to-check-little-vs-big-endian)
* [A Tutorial on Data Representation](https://www3.ntu.edu.sg/home/ehchua/programming/java/datarepresentation.html)
* [CPU Cache 原理探討](https://hackmd.io/s/H1U6NgK3Z)
* [Computer Architecture Notes](https://hackmd.io/s/rkloHgHcx)
* [計算機組織結構](https://hackmd.io/s/H1sZHv4R)
* [CSAPP-3e-Solutions](https://github.com/DreamAndDead/CSAPP-3e-Solutions)