Note 08: Sorting Algorithms - [Homepage](http://gddh.github.io/)
==================

# MergeSort

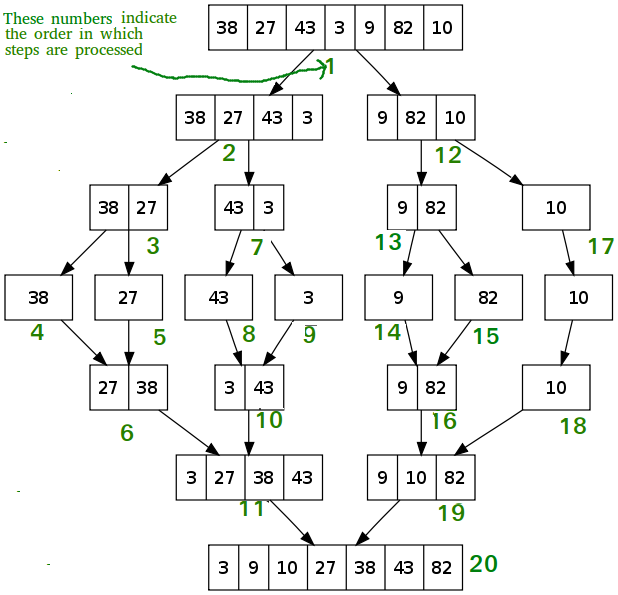
### Brief Description:
1. recursively divides the array by halves until each element is its own array
2. merges the individual elements into sorted arrays
3. merges sorted array

<table>
<tr>
<th>Best Case</th>
<th>Average Case</th>
<th>Worst Case</th>
<th>Array Space</th>
<th>Linked List Space</th>
</tr>
<tr>
<td>Ω(n log n)</td>
<td>Θ(n log(n))</td>
<td>O(n log(n))</td>
<td>O(n)</td>
<td>O(log n)</td>
</tr>
</table>

### Runtime Analysis
Merge sort is a divide and conquer algorithm.

Thus write a recurrence relation: T(n) = 2T(n/2) + Θ(n).
Master's Theorem: T(n) = aT(⌈n/b⌉) + O(n^d)
Using Master's theorem we see that the runtime is (n logn) no matter what.

An intuitive argument would be that we are building two trees and at each level we handle n elements.

### Space Analysis
#### Array Implementation - O(n)
Observe that the worst case scenario for space is O(n) because we will need to use a temporary array to merge the sublists. The largest two temporary arrays would be each 1/2 n.

Note that the space is taken up in ``merge``.

#### Linked List Implementation - O(log n)
Observe that ``merge`` is actually happening in place. We create a new head node to be returned, which is O(1). (To clarify, consider the array implementation where we created O(n) sized array. Here we aren't creating anything with respect to n).

Another way of looking at it is that linked list require O(1) time to add elements, therefore merge operations will take O(1).

However, we still need to account for the space that the recursive calls take up. There are log n recursive calls.

### Implementation Tips
**Note** These implementation tips are meant to shadow my implementation thought process. Your implementation/thought process may be different or you may come across a different set of challenges. So these may not necessarily be relevant to you.

Two main steps that apply to both implementation
1. recursively dividing the elements until they are singular units
- Use the midpoint as the point to divide with
3. merging the elements by twos
- Keep "merging" until one of the "halves" is exhausted
- Add on the half that is not exhausted

#### Array Implementation
- In order to modify the original array, we will need temporary arrays to hold the original value
- Notice that temporary arrays require sizes
- Use a ```mid``` variable to calculate sizes

#### Linked List Implementation
- First write the ```merge``` function - merges two sorted arrays
- to find the midpoint use two pointers. One that skips a link, while the other traverses each link. When the one skipping reaches the end, the one traversing each link will be at the midpoint.
- Merging requires two sorted arrays. In order to achieve these arrays, we cannot just create pointers to our original array because this will cause a "staggered repitition." This means in addition to creating pointers, we also need to "break" our original list into sublists.

### Usage:
#### Sorting Linked Lists
- does not require random selection of elements. If we were to use something like quick sort, where we would randomly select an element, we would need to traverse through the list each time to randomly select. Merge sort doesn't do that.
- Space complexity is low

#### Inversion Problem
- The inversion count problem: How many inversions/swaps will a sort require to completely sort the array
- In the merge step, there is at least one inversion if the element from the "right-hand side" sorted array is less than the element from the "left-hand side" sorted array. We can calculate the number of inversion per comparison by ```m - l + 1```. Keep track of running sum.
- inversion pairs such that A[i] > A[j]
- By using merge sort, we beat the runtime for the brute force solution, which is O(n^2)
- Applicable to MapReduce
- Map Reduce Refresher:
- http://stevekrenzel.com/finding-friends-with-mapreduce
- https://stackoverflow.com/questions/22141631/what-is-the-purpose-of-shuffling-and-sorting-phase-in-the-reducer-in-map-reduce
- https://developer.yahoo.com/hadoop/tutorial/module4.html#dataflow
- Merge sort is used in reduce side. Merge sort is the default feature of MapReduce. Data comes from the different nodes to a single point, so the best algorithm that can be used here is the merge sort.

# Quick Sort

<table>
<tr>
<th>Best Case</th>
<th>Average Case</th>
<th>Worst Case</th>
<th>Array Space</th>
</tr>
<tr>
<td>Ω(n)</td>
<td>Θ(n log n)</td>
<td>O(n^2)</td>
<td>O(log n)</td>
</tr>
</table>

### Runtime Analysis
Quick Sort's runtime largely depends on the input and the choice of pivot with respect to the input. Because of the randomness in possible inputs and the difference of choice of pivot, we break down the runtime of quicksort into the following three cases.

#### Best Case
The best case is when the pivot evenly divides the list. Wikipedia expresses this concisely:

Each time we perform a partition we divide the list into two nearly equal pieces. This means each recursive call processes a list of half the size. Consequently, we can make only log_2(n) nested calls before we reach a list of size 1. This means that the depth of the call tree is log_2(n). But no two calls at the same level of the call tree process the same part of the original list; thus, each level of calls needs only O(n) time all together (each call has some constant overhead, but since there are only O(n) calls at each level, this is subsumed in the O(n) factor).

The result is O(n log n).

#### Average Case
The average case is O(n log n).

Let us understand this intuitively:

- Divide the array into 4 equal sections:

- Observe the elements in ```B``` and ```C``` form 1 / 2 the elements.

- Therfore on average, half of times our chosen pivots will **at least** partition the elements into partitions that include 1 / 4 and 3 /4 of the relevant subarray.

- *For simplicity let us assume* that everytime our chosen pivots will **at least** partition the elements into partitions composed of 1 / 4 and 3 /4 of the elements in the relevant subarray.

- This means that in the worst case, we will make log_{3/4}(n) recursive calls before we hit the base case. 
    - Why log_{3/4}(n)?
        - Consider we start at 1. How many times would we need to multiply by 4/3 until we get to n?
        - Mathematically this question can be rephrased as solving for x: (4/3)^x = n
            - x = log_{3/4} = n
        - The number of times we need to multiply by 4/3 tels us the number of recursive calls because under our assumptions the biggest argument to a recursive call will be 3/4 of the current array. Therefore our problem in the worst case is being divided by 3/4
        - In other words,
            - number of times we would need to multiply by 4/3 to get n starting from 1 == the number of times we would need to divide by 3/4 to get 1 starting from n

- Retract our assumption of ignoring the half of the times where our parititions will not create partitions of 1 / 4 and 3 /4. Thus, in worst case, half of our paritions will be composed of 1 element and n-1 elements.
- Let us now observe in worst case scenario (with randomness when partitioning):
    - half of the time, our recursive calls will make progress by dividing elements into at least paritions of 1 / 4 and 3 / 4, while the other half of the time, o
    - other half of the time, our recursive calls will essentially make no progress because partitions of 1 and n - 1 elements basically leaves the subproblem with n elements.
    - Therefore we are making progress half of our recursive calls. So if we double the recursive calls, we should be able to hit the base case and complete our task.
- The *total* partitioning time for each subproblem/subarray of a particular size is ```cn``` where ```c``` is some constant.
- Thus we have 2(cn log_{3/4} n) as our runtime. 
    - 2(cn log_{3/4} n) = O(nlog_n)

Further clarification: https://www.khanacademy.org/computing/computer-science/algorithms/quick-sort/a/analysis-of-quicksort

#### Worst Case
The worst case is when the element chosen as the pivot is the smallest or largest element in the relevant subarray. (In some implementations, another worst case is when there are many of the same elements in the relevant subarray) 

This is the worst case because the argument to the recursive call will be an array that is smaller by just one element. Therefore, we will make n recursive calls with each recursive call going through the elements in the relevant subarray.

The total number of elements that are processed will be the sum: n + (n - 1) + ... + 2 + 1 = ((n)(n + 1)) / 2 = O(n^2)

### Space Analysis
Simple quick sort in the worst case requires O(n) recursive calls. 

QuickSort Tail Call Optimization has O(log n) for space complexity.
- By using recursion only on the smaller half, we guarantee that the amount of recursive calls will be at most log n recursive calls. 
    - This is because in the worst case scenario for space, we will evenly partition the relevant subarray.
    - Where did the other recursive calls go?
        - We take care of it using iteration and "tail calls." The "tail calls" allow us to minimize the depth of the recursion, moving most of the work to the iteration. The iteration is done in one frame.
        - Further reading: 

            - https://www.geeksforgeeks.org/quicksort-tail-call-optimization-reducing-worst-case-space-log-n/
            - This one has a slight mistake I think... The following stack overflow link addresses it. http://mypathtothe4.blogspot.com/2013/02/lesson-2-variations-on-quicksort-tail.html
            - https://stackoverflow.com/questions/19854007/what-is-the-advantage-of-using-tail-recursion-here
            - https://stackoverflow.com/questions/19094283/quicksort-and-tail-recursive-optimization

### Implementation Tips
- The overall algorithm consists of three steps:
    - partition
    - recursively quick sort the left of the partition
    - recursively quick sort the right of the partition
- When partitioning we can choose which element to use as the partition in many ways:
    - Last element
    - First element
    - Median
    - Random

- Partitioning
    - **Original Approach** was figuring out how to place the pivot in the proper position and then swapping elements smaller than the pivot to the left and elements larger than the pivot to the right.
    - **Better Approach** was figuring out how to move elements smaller than the pivot to the left THEN placing the pivot in the proper position:
        - Isolate the pivot and iterate through the array while moving the elements smaller than the pivot to the left of the array. Then place the pivot 
        - To collect the elements left of the array, use two pointers 
            - Pointer, ```p_a```, keeps track of potential space for elements to the left of the pivot 
            - Pointer, ```p_b```, iterates through the nonpivot index and swaps with ```p_a```.
            - Refer to "Illustration of partition()" for example of partitioning process: https://www.geeksforgeeks.org/quick-sort/
        - Place the partition to the right of the elements that have been moved to the left of the array.
        - return the partition
    - If your choice of pivot is not the right most element, you can first take your pivot and swap it with the right most element and perform the same operations

- Optimizations
    - Take medians of a couple of randomly chosen elements and use that as a pivot. The more you pick the better chances of balanced partitions.
    - Given information on the data, you may be able to choose the position of your pivot such that you evenly divide the array.
    - Space can be optimized by tail call optimization.
    

## Quick Sort vs. Merge Sort
- Both Divide and Conquer Algorithms
    - We can use Master Theorem to analyze the run time.
- In merge sort, the divide step does hardly anything, and all the real work happens in the combine step. Quick sort is the opposite: all the real work happens in the divide step
- In practice, quick sort outperforms merge sort, and it significantly outperforms selection sort and insertion sort.
- Quick sort is not stable. Merge sort is stable.
- Quick sort is cache friendly (it has good locality of reference when used for arrays.)
- Quick sort is usually an in-place sort (doesn’t need extra storage). Merge sort requires O(N) extra storage, where N is array size. This can be expensive.
- Merge sort is preferred for Linked Lists because may not be adjacent, so accessing memory randomly will be more costly for quick sort.

# Selection Sort
(CS61B - Professor Hug): Repeatedly identifying the most extreme element and moving it to the end of the unsorted section of the array. The naive implementation of such an algorithm is in place.

<table>
  <tr>
    <th>Best Case</th>
    <th>Average Case</th>
    <th>Worst Case</th>
    <th>Array Space</th>
  </tr>
  <tr>
    <td>Ω(n^2)</td>
    <td>Θ(n^2)</td>
    <td>O(n^2)</td>
    <td>O(1)</td>
  </tr>
</table>

### Runtime Analysis
In selection sort, we go through the entire array and at each step we consider **all** the remaining elements.

To be explicit let's consider the example: 1, 3, 2, 4, 5
Step 1: 1, 3, 2, 4, 5
Step 2: 3, 2, 4, 5
Step 3: 3, 4, 5
Step 4: 4, 5
Step 5: 5
Therefore: 5 + 4 + 3 + 2 + 1

Generalizing: n + n - 1 + ... + 1 = (n(n + 1)) / 2 = O(n)

### Space Analysis
Since we are working in place, selection sort is O(1)

# Sorting with Stacks

Sort a stack using 1 temporary stack. 

## How it works - Sort in Ascending Order

**Note 1**
If the elements in the stack are oriented in descending order, the stack is sorted in ascending order.

To be clear

stack : 4 3 2 1

pop(stack) --> 1
pop(stack) --> 2
pop(stack) --> 3
pop(stack) --> 4

**Note 2**
Consider two stacks:

stack1: 1 2 3 4 # this is sorted in descending order. Consider popping it.
stack2:

If I pop everything from stack1 and push it onto stack 2.

stack1:
stack2: 4 3 2 1 # now sorted in ascending order

**Observe: ** If we can get stack1 in descending order and then just pop and push into stack2, then stack2 will be sorted in ascending order.

**Note 3**
Consider the following example of getting elements of stack1 into stack2 in ascending order:

stack1: 1 3 2 4 5
stack2:

stack1: 1 3 2
stack2: 5 4

- If we just pop 2 and push it into stack2, we won't have stack2 in descending order.
    - The problem here is that 2, the top of stack1, is smaller than 4, the top of stack2.
- 2 must appear before 4 in stack 2.
    - How can we acheive this?
        - One idea is to hold onto the 2 in a variable. 
        1. Then pop and push all of stack2 into stack1.
        2. Then push cur into stack2
        3. Then pop and push the elements originally in stack2 back into stack2

1.
stack1: 1 3
stack2: 5 4
cur : 2

2.
stack1: 1 3 4 5
stack2: 2
cur :

3.
stack1: 1 3
stack2: 2 4 5

If we do the same process for all elements in stack1, then we can get stack 2 in descending order. 

Given a stack 2 in descending order, we just need to pop and push everything into stack1 for stack1 to be in ascending order.

### Runtime

The worst case is a stack that starts in descending order. For each element, we will have to move what is already on the temp stack (stack 2) back onto the original stack (stack 1).  This number will grow from 1 to n - 1. This means we will have 1 + 2 + .... + n - 1 movement. Thus O(n^2)