# [2016q1 Homework #1](http://wiki.csie.ncku.edu.tw/embedded/2016q1h1)

## 預期目標

* 準備 GNU/Linux 開發工具
* 學習使用 Git 與 GitHub
* 學習效能分析工具
* 研究軟體最佳化

**lscpu | grep cache**

* L1d cache:             32K
* L1i cache:             32K
* L2 cache:              256K
* L3 cache:              6144K

## 實作的優化方法

**改善資料結構**

1.修改structure結構，使得structure裡頭只有lastName實際佔空間，由於原本的structure太大所以一個cache沒辦法放入很多結構所以改小structure

**改善搜尋演算法**

2.HASH

3.BST

4.AVL Tree

**修改Makefile與scripts/runtime.gp**

[參考](https://xn--[]-fs3g/#ifndef, #define, #endif的用法(整理)) 中的#ifdef及老師的 #if defined() 可以改出直接下make plot就自動幫忙畫好所有的圖

優點是我可以把所有程式碼集中在一份(phonebook_opt.c)裡面,只要修改Makefile裏頭的參數即可做出不同功能

## 效能分析

**優化前**

* perf stat --repeat 100 \
* -e cache-misses,cache-references,instructions,cycles \
* ./phonebook_orig
* size of entry : 136 bytes
* execution time of append() : 0.049326 sec
* execution time of findName() : 0.005799 sec

* Performance counter stats for ’./phonebook_orig’ (100 runs):

* 2,050,363 cache-misses              #   90.245 % of all cache refs      ( +-  0.05% )
* 2,272,002 cache-references                                              ( +-  0.02% )
* 268,736,633 instructions              #    1.27  insns per cycle          ( +-  0.02% )
* 211,278,740 cycles                     ( +-  0.10% )

* 0.066504571 seconds time elapsed                                          ( +-  0.40% )

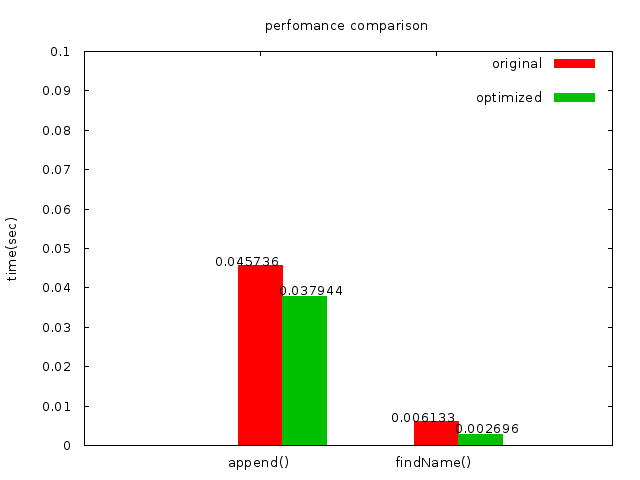
**Case1(減小資料結構)**

利用調整struct大小來增加裝載在cache裡的資料數，進而降低cache miss


* perf stat --repeat 100 \
* -e cache-misses,cache-references,instructions,cycles \
* ./phonebook_opt
* size of entry : 32 bytes
* execution time of append() : 0.043508 sec
* execution time of findName() : 0.002599 sec
* Performance counter stats for ’./phonebook_opt’ (100 runs):

* 399,508 cache-misses              #   59.302 % of all cache refs      ( +-  0.14% )
* 673,682 cache-references                                              ( +-  0.12% )
* 248,104,990 instructions              #    1.69  insns per cycle          ( +-  0.02% )
* 147,185,970 cycles                     ( +-  0.18% )

* 0.046546887 seconds time elapsed                                          ( +-  0.58% )

可以由上面的結果知道改上資料結構可以減少cache miss的程度

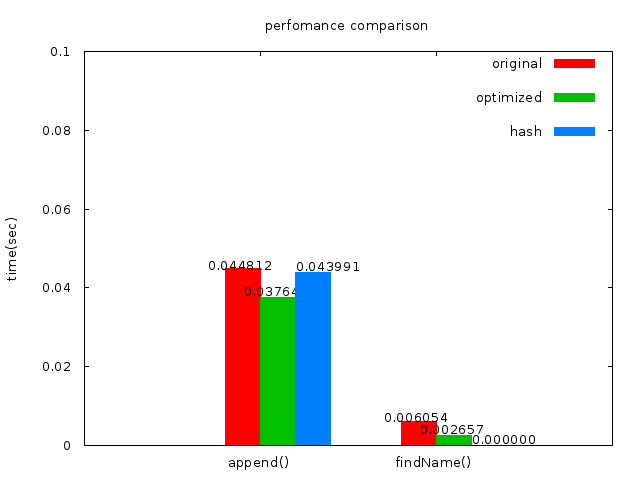
**Case2(HASH)**

我的hash function如下

* int hash31(char *s)
* {
* unsigned value = 0;
* for (; (*s) !=’\0’; s++)
* value = (value << 5) - (value + (*s));
* return value % HASH_TABLE_SIZE;
* }

* hash_table size = 1000


* perf stat --repeat 100 \
* -e cache-misses,cache-references,instructions,cycles \
* ./phonebook_hash
* size of entry : 32 bytes
* execution time of append() : 0.017986 sec
* execution time of findName() : 0.000000 sec
* Performance counter stats for ’./phonebook_hash’ (100 runs):

* 15,437 cache-misses              #   25.774 % of all cache refs      ( +-  3.01% )
* 59,894 cache-references                                              ( +-  0.75% )
* 94,543,925 instructions              #    1.61  insns per cycle          ( +-  0.00% )
* 58,634,626 cycles                     ( +-  0.22% )

* 0.019716930 seconds time elapsed                                          ( +-  1.35% )

雖然append的時間稍稍上升了,但是在findName上面的時間幾乎趨近於0

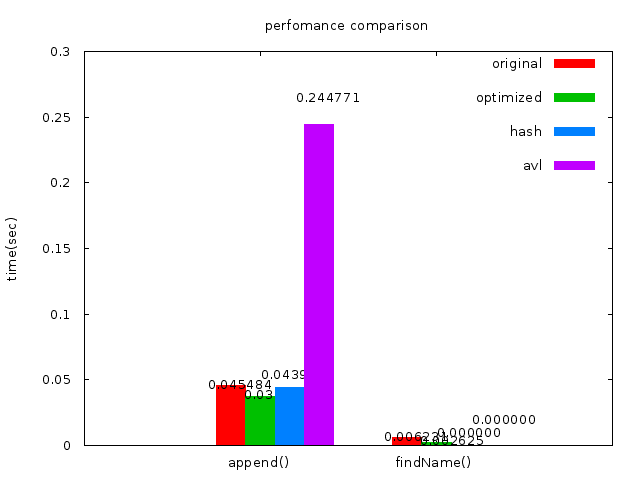
**Case3([AVL Tree](http://www.geeksforgeeks.org/avl-tree-set-1-insertion/))(trie)**

我把BST跟AVL tree放在一起因為在這個phonebook的例子裡面BST tree會退化成為一條直線因為原始的資料是已經有排序好的，使得append的時間會高達400多秒。原因是因為每次在append時都要從tree 的root開始搜尋

後來使用AVL Tree，AVL tree的好處是可以隨時調整樹的高度，讓樹能夠很平均


* size of entry : 48 bytes
* execution time of append() : 0.248442 sec
* execution time of findName() : 0.000000 sec

* Performance counter stats for ’./phonebook_avl’ (100 runs):

* 373,119 cache-misses              #   52.815 % of all cache refs      ( +-  0.26% )
* 706,460 cache-references                                              ( +-  1.69% )
* 1,280,608,877 instructions              #    1.59  insns per cycle          ( +-  0.00% )
* 807,487,367 cycles                     ( +-  0.08% )

* 0.247392619 seconds time elapsed                                          ( +-  0.15% )

在append的時間增加了,但是findName的時間也是趨近於0

p.s. 0.0000的部分我已經有用gdb驗證過了,實際上是有找到的

## Levenshtein Distance （編輯距離）

參考[李詔遠同學得hackpad](https://charles620016.hackpad.com/Charles-Week-6-HW5-Japi4qFyAzt)來實作fuzzy search

**Fuzzy Search**

Fuzzy Search 根據問題大概可以分兩類，一個是從已知的字串推斷出可能的單字或句子，另一個是從字典或是資料庫裡面找出相似的 pattern，而這次目標就是實現後者。

在[Fuzzy string search](http://ntz-develop.blogspot.tw/2011/03/fuzzy-string-search.html)這篇文章有更詳盡的介紹

[Levenshtein Distance](https://en.wikipedia.org/wiki/Levenshtein_distance) 又叫做編輯距離 ( Edit Distance )，是 1965 年由研究資訊理論、錯誤更正碼、組合設計的俄羅斯科學家 Vladimir Levenshtein 所提出來的概念。 是指一個字串轉換成為另外一個字串所需的最少「編輯操作」次數，所謂的編輯操作可以是替換字元、插入字元、刪除字元，是個用來衡量兩字串相似度的重要指標。

例如將`kitten`轉成`sitting`：

* step 1: kitten → sitten  (**substitution** of "s" for "k")
* step 2: sitten → sittin  (**substitution** of "i" for "e")
* step 3: sittin → sitting (**insertion** of "g" at the end)

數學式子如下，[indicator function](https://en.wikipedia.org/wiki/Indicator_function) 是指示函數，括弧內為此函數等於 1 時的條件。


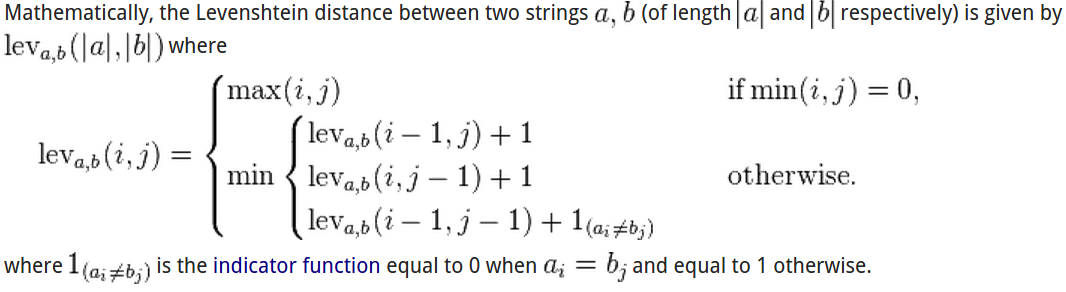
實際上實作有兩種recursive 與iterative

recursive的code就長得跟數學式差不多，[參考](https://en.wikipedia.org/wiki/Levenshtein_distance)

* _// len_s and len_t are the number of characters in string s and t respectively_int LevenshteinDistance(string s, int len_s, string t, int len_t){ int cost;

* _/* base case: empty strings */_
* **if** (len_s == 0) **return** len_t;
* **if** (len_t == 0) **return** len_s;

* _/* test if last characters of the strings match */_
* **if** (s[len_s-1] == t[len_t-1])
* cost = 0;
* **else**
* cost = 1;

* _/* return minimum of delete char from s, delete char from t, and delete char from both */_
* **return** minimum(LevenshteinDistance(s, len_s - 1, t, len_t    ) + 1,
* LevenshteinDistance(s, len_s    , t, len_t - 1) + 1,
* LevenshteinDistance(s, len_s - 1, t, len_t - 1) + cost);}