# 演算法 (Alogrithm)
> AndyLee 2017.5.3
## 1.演算法(Algorithm)
- 為問題的解決過程中,先做問題的描述,有系統的規劃安排,最後再透過某種能與電腦溝通的介面來讓電腦來執行,就是一種「計算方法或法則」。
- 或者也可以將演算法看成是解決某一個工作或問題,所需要的一些有限個數的指令或步驟。
## 2. 演算法需要具備以下五大基本原則:
- 有限性(Finiteness)
必須在有限的步驟內解決問題,不可造成無窮迴路。
- 有效性(Effectiveness)
每一個步驟或運算若交給人們用筆或紙計算,也能在有限時間內達成同樣效果。
- 明確性(Definiteness)
每一個步驟或指令必須要敘述的很清楚,不可以模糊不清。
- 輸入資料(Input)
演算法的輸入資料可有可無,零或一個以上都可以。
- 輸出資料(Output)
演算法的結果一定要有一或一個以上的輸出資料。
## 2. Space Complexity : 是執行完成一個程式所需要的記憶體大小。
下面這個函式,會隨著丟進去的數字而影響變數的量,例如:
```clike=
funtcion(int n){
int c[n];
for(int i=0;i<n;i++){
c[i] = i;
}
}
```
丟進去 n,就換產生 n 個變數,故該函式空間複雜度為 O(n)。
## 3. Time Complexity:是指一個程式從開始到執行完成總共所需要花費的執行時間。
O(1)< O(logn)< O(n)< O(nlogn)< O(n^2^)< O(n^3^)< O(2^n^)< O(n!)
## Greed Alogrithm (貪婪演算法)
貪婪演算法(Greedy algorithm)是指在對問題求解時,==總是做出在當前看來是最好的選擇。==
也就是說,不從整體上最優(global optimization)加以考慮,所做出的僅是在某種意義上的局部上最優的解(local optimization)。
貪心演算法不是對所有問題都能得到整體最優解,但對範圍相當廣泛的許多問題他能產生整體最優解或者是整體最優解的近似解。
**Example : 要把 n 個 1 元硬幣兌換成 50 元, 10 元, 5 元, 1 元硬幣, 如何兌換可以讓最終的硬幣數最少?**
每一步都不管大局, 只求這一步換掉越多 1 元硬幣越好。
1. x~0~ = floor(n / 50); n = n % 50;
2. x~1~ = floor(n / 10); n = n % 10;
3. x~2~ = floor(n / 5) ; x3 =n % 5 ;
則 "x~0~ 個 50 元, x~1~ 個 10 元, x~2~ 個 5 元, x~3~ 個 1 元" 即為答案。
## Dynamic Programming(動態規劃)
動態規劃是分治法的延伸。當遞迴分割出來的問題,一而再、再而三出現,就運用==記憶法儲存這些問題的答案,避免重複求解,以空間換取時間。==
動態規劃的過程,就是反覆地讀取數據、計算數據、儲存數據
- 動態規劃類似Divide and Conquer,一個問題的答案來相依於子問題,常用來解決**最佳解**的問題。
- 與Divide and Conquer不同的地方在於,動態規劃多使用了**memoization的機制**,將處理過的子問題答案記錄下來,避免重複計算,因此在子問題重疊的時候應該使用動態規劃
- 動態規劃是分治法的延伸。當遞迴分割出來的問題,一而再、再而三出現,就運用記憶法儲存這些問題的答案,避免重複求解,以空間換取時間。
- 簡言之:「計算並儲存小問題的解,並將這些解組合成大問題的解。」
### Time Complexity
總共 N 個問題,每個問題花費 O(1) 時間,總共花費 O(N) 時間。
### Space Complexity
求 1! 到 N! :總共 N 個問題,用一條 N 格陣列儲存全部問題的答案,空間複雜度為 O(N) 。
### 費波那西數列(Fibonacci)例子
```
function Fibonacci(n)
if n == 0
return 0
if n == 1
return 1
return Fibonacci(n - 1) + Fibonacci(n - 2)
```
```
var map // cache of fibonacci
map[0] = 0
map[1] = 1
function Fibonacci(n)
if map[n] == null
map[n] = Fibonacci(n - 1) + Fibonacci(n - 2)
return map[n]
```
### 最大子序列(Maximum Subarray)例子
最大子序列(Maximum Subsequence)為Kadane's演算法(Dynamic Programming)在一個具有正負數陣列當中,找出一段連續的元素總和最大。
Kadane's演算法(Dynamic Programming)
```
// O(n), Kadane's 演算法(dynamic porgramming), 可不取版本
public class Kadanes {
public static int GetMax(int[] array)
{
int sum = 0;
int max = array[0];
for (int i = 0; i < array.length; ++i)
{
sum += array[i];
sum = Math.max(0, sum);
max = Math.max(sum, max);
}
return max;
}
}
```
Reference:
1. https://goo.gl/Dh36rW
2. https://goo.gl/uQnxAo
---
# Sorting Algorithm
| | Quick Sort | Merge Sort | Heap Sort | Insertion Sort | Selection Sort | Bubble Sort
| --- | --- | --- | --- | --- |---|----|
| Best case | N log N | N log N | N log N | N | N^2^ |N|
| **Average case** | N log N | N log N | Nlog N | N^2^ | N^2^ |N^2^|
| Worst case | N^2^ | NlogN | NlogN | N^2^ | N^2^ |N^2^|
Reference:
http://spaces.isu.edu.tw/upload/18833/3/web/sorting.htm
## Bubble Sort
氣泡排序法(Bubble Sort)是排序演算法的一種,其觀念是==逐次比較相鄰的兩筆資料,不斷將最大的元素擠出(移動)到陣列最尾端==,當所有元素都如同氣泡般被被擠出後,排序就完成了!
氣泡排序演算法的運作原理如下:
1.比較相鄰的元素,如果第一個元素比第二個元素大(小),就交換這兩個元素。
2.對每一對相鄰的元素執行同樣的行為,從開始的第一對到結尾的最後一對。當這步做完之後最後的元素會是最大的數。
3.針對除了最後一個已經排序過後的數之外重複步驟一跟步驟二。
4.持續每次對越來越少的未排序的元素重複上面的步驟,直到沒有任何一對數字需要比較。
執行時,未排序資料中的**最大值**會如同氣泡般往右邊移動,故此命名為氣泡排序法。
:::info
* 最佳時間複雜度:O(n) 當資料的順序恰好是所選擇的排序方式時。
* 平均時間複雜度:O(n^2^) 第n筆資料,平均比較(n-1)/2 次。
* 最差時間複雜度:O(n^2^) 當資料的排序恰好是所選擇的相反排序方式。
:::
```clike=
public class BubbleSort {
public static void Sort(int[] array)
{
for (int i = array.length - 1; i > 0; --i){ //i 從length-1 ~
for (int j = 0; j < i; ++j){ ////iterate每一個item跟旁邊item比較
if (array[j] > array[j + 1])
Swap(array, j, j + 1);
}
}
}
private static void Swap(int[] array, int a, int b)
{
int tmp = array[a];
array[a] = array[b];
array[b] = tmp;
}
}
```
### bubble sort 優化
若序列已經是排序狀態了,每一次for(int i )裡面都要再做一次for(int j ),這樣太浪費時間跟內存
下面是優化過的版本,主要是加上一個flag紀錄序列是否已經是排序好的了
```clike=
public static void bubbleSort(final int[] array) {
for (int i = array.length - 1; i > 0; i--) {
boolean sorted = true; // 紀錄接下來for (int j = 0; j < i; ++j)是否排序過了
for (int j = 0; j < i; j++) {
if (array[j] > array[j+1]) {
int buffer = array[j];
array[j] = array[j+1];
array[j+1] = buffer;
sorted = false; //有需要排序的
}
}
if (sorted) { // 若sorted==true,代表數列都已經是排序好了!就BREAK不做了
break;
}
}
}
```
---
## Selection Sort
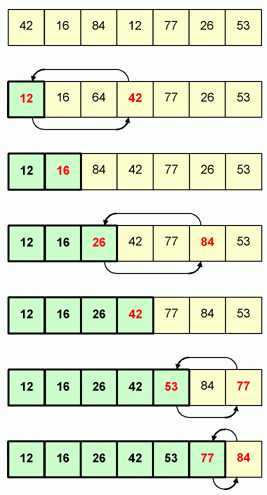
選擇排序的原理是==每次都在剩下的資料中找出最小的資料,將該資料丟到當前的正確位置==
也就是說將第 i 筆到第 n 筆資料中排出最小值,與第 i 筆資料做交換。
每回合自第 i 筆到第 n 筆中排出最小值,與第 i 筆資料做交換
:::info
最佳時間複雜度:O(n^2^)
平均時間複雜度:O(n^2^)
最差時間複雜度:O(n^2^)
:::
```clike=
public void selectionSort(int[] arr) {
int i, j, minIndex, tmp;
int n = arr.length;
for (i = 0; i < n - 1; i++) {
minIndex = i; //假設目前最小值是i
for (j = i + 1; j < n; j++){
if (arr[j] < arr[minIndex])
minIndex = j;
// 交換arr[i]與arr[minIndex]
tmp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = tmp;
}
}
}
```
***
## Insertion Sort
Insertion Sort的方法為:將第i張紙牌加入「前i−1張排序過」的紙牌組合,得到i張排序過的紙牌組合。
從左邊數來的前三張紙牌已經排好序:index(0)、index(1)、index(2)分別為1、3、51、3、5,現在要將第四張紙牌(index(3),數值為22)加入前三張牌,想要得到「前四張排好序」的紙牌組合。
經由觀察,最終結果的紙牌順序為1、2、3、51、2、3、5,可以透過以下步驟完成:
原先index(2)的5搬到index(3);
原先index(1)的3搬到index(2);
原先index(3)的2搬到index(1);
如此便能把第4張紙牌加入(insert)「前3張排序過」的紙牌組合,得到「前4張排序過」的紙牌組合。
由以上說明可以看出,Insertion Sort要求,在處理第i筆資料時,第1筆至第i−1筆資料必須先排好序。
:::info
* 最佳時間複雜度:O(N
要處理的序列是1、2、...、N **當問題已經「接近完成排序」的狀態時,使用Insertion Sort會非常有效率**。
* 平均時間複雜度:O(N^2^)
* 最差時間複雜度:O(N^2^)
若要處理的序列恰好是顛倒順序,N、N−1、...、2、1,那麼位於index(i)的元素,需要比較「i−1次」。
:::
```clike=
void InsertionSort(int *arr, int size){
for (int i = 1; i < size; i++) {
int key = arr[i];
int j = i - 1;
while (key < arr[j] && j >= 0) { //不斷比較arr[i] and arr[i-1],直到最小值在左邊
arr[j+1] = arr[j]; //swap
j--; //向左移,再做一次while
}
arr[j+1] = key; //最後把最左邊的給值key
}
}
```
## Merge Sort
合併排序法(或稱歸併排序法),是排序演算法的一種,使用[Divide and Conquer](http://emn178.pixnet.net/blog/post/87739443)的演算法來實作。
排序時需要額外的空間來處理,過程依照以下步驟進行:
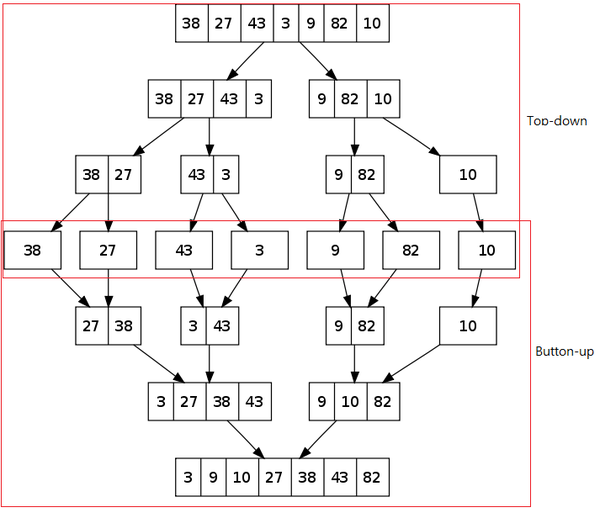
1. 將陣列分割直到只有一個元素。
2. 開始兩兩合併,每次合併同時進行排序,合併出排序過的陣列。
3. 重複2的動作直接全部合併完成。
流程範例如圖所示:
:::info
最佳時間複雜度:O(nlog n)
平均時間複雜度:O(nlog n)
最差時間複雜度:O(nlog n)
:::
```clike=
class MergeSort {
public static void main(String args[]) {
int arr[] = { 12, 11, 13, 5, 6, 7 };
System.out.println("Given Array");
printArray(arr);
MergeSort ob = new MergeSort();
ob.sort(arr, 0, arr.length - 1);
System.out.println("\nSorted array");
printArray(arr);
}
// Main function that sorts arr[l..r] using merge()
void sort(int arr[], int l, int r) {
if (l < r) {
// Find the middle point
int m = (l + r) / 2;
// Sort first and second halves
sort(arr, l, m);
sort(arr, m + 1, r);
// Merge the sorted halves
merge(arr, l, m, r);
}
}
// Merges two subarrays of arr[]
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r) {
// Find sizes of two subarrays to be merged
int n1 = m - l + 1;
int n2 = r - m;
/* Create temp arrays , need additional space*/
int L[] = new int[n1];
int R[] = new int[n2];
/* Copy data to temp arrays */
for (int i = 0; i < n1; ++i)
L[i] = arr[l + i];
for (int j = 0; j < n2; ++j)
R[j] = arr[m + 1 + j];
/* Merge the temp arrays */
int i = 0, j = 0;
// Initial index of merged subarray
int k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
/* Copy remaining elements of L[] if any */
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
/* Copy remaining elements of R[] if any */
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
static void printArray(int arr[]) {
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
}
```
## Quick Sort
Quick sort排序演算法是普遍被認為最快的排序演算法,與Merge Sort 一樣,都採用 divide & conquer 的策略。
Quick sort 的切割方式為,每次從數列中選出一個元素作為 pivot(支軸),並將剩餘的元素分為兩堆,一堆是小於 pivot 的元素,另一堆是大於 pivot 的元素,至於相等的隨便放就好。
:::info
- Best Case:Ο(nlogn):第一個**基準值**的位置剛好是中位數,將資料均分成二等份
- Worst Case:Ο(n^2^) :當資料的順序恰好為由大到小或由小到大時
- Average Case:Ο(nlogn)
:::
```clike
#include <stdio.h>
#include <stdlib.h>
void print(int *data, int n);
void quicksort(int *data, int left, int right);
void swap(int *a, int *b);
int main(void)
{
int data[] = {5,4,1,2,3};
int n = sizeof(data)/sizeof(int);
print(data, n);
quicksort(data, 0, n - 1);
print(data, n);
return 0;
}
void print(int *data, int n){
for(int i = 0 ; i < n ; i++)printf("%d ",data[i]);
printf("\n");
}
void quicksort(int *data, int left, int right)
{
if (left >= right) { return; }
int i, j;
int pivot = data[left]; // pivot = data[0]
i = left + 1;
j = right;
while (1){
// 向右找大於Pivot的第一個數值的位置
while (i <= right){
if (data[i] > pivot) break;
i++;
}
// 向左找小於Pivot第一個的數值的位置
while (j > left){
if (data[j] < pivot) break;
j--;
}
// 若i,j的位置交叉,代表範圍內,Pivot右邊已無比Pivot小的數值,Pivot左邊已無比Pivot大的數值
if (i > j) {break;}
// 將比Pivot大的數值換到右邊,比Pivot小的數值換到左邊
swap(&data[i], &data[j]);
}
swap(&data[left], &data[j]); // 將Pivot移到中間
quicksort(data, left, j - 1);// 對左子串列進行快速排序
quicksort(data, j + 1, right);// 對右子串列進行快速排序
}
void swap(int *a, int *b){
int temp = *a;
*a = *b;
*b = temp;
}
```
## Heap Sort
---
# Search Alogrithm
## Binary Search
二元搜索法(Binary Search)又稱折半搜索,搜索演算法的一種,可使用[Divide and Conquer](http://emn178.pixnet.net/blog/post/87739443)或直接使用迴圈來實作,搜索的目標資料必須是已經排序過的(以小到大排序為例)。其概念是每次挑選中間位置的資料來比對,若該資料小於目標值,則縮小範圍為左半部,反之亦然;因此使用這個方法每次比對後都可以濾掉一半的資料,以增快搜索速度。
過程如下:
1. 取出搜索範圍中點的元素。
2. 與搜索目標比較,若相等則回傳位址。若小於則將左邊邊界改為中點右側,若大於則將右邊邊界改為中點左側。
3. 左邊邊界不超過右邊邊界(還有資料)則重複以上動作,若已無資料則回傳-1(找不到)。
:::info
最佳時間複雜度:O(1)
平均時間複雜度:O(log n)
最差時間複雜度:O(log n)
空間複雜度:O(1)
:::
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet