# Optimizing matrix multiplication

###### tags: `aweimeow`, `sysprog`, `Team3`

---

## Basic Matrix Multiple Introduce


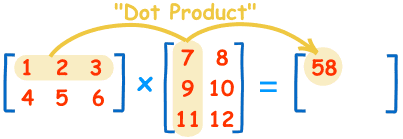
Let start from a short sweet multiply code:

for i = 1 to m
	for j = 1 to m
		for k = 1 to m
			C(i, j) = C(i, j) + A(i, k) * B(k, j)

## Optimization Techniques

### L1 cache blocking optimizations

Partition Big Matrix into uniform matrix, muitiply matrix in L1 cache, and then self-interface misses are minimized.

##### Calculate Optimal block size

> $2 * (blockSize)^2 * wordSize = L1cachesize$

* blockSize: uniform matrix size
> 文章中是以2的倍數，因為 L1 cache 一行有 4 words 的大小，選其他倍率效能會很差。
> 觀察從16到64之間 block sizes 效能設定。

* wordSize: Datatype in matrix (ex. double: 8 bytes)

### Compile flag Optimizations

gcc provide various compiling options, and `-O4`, `-funroll-loops`, `-ffast-math`, but `-ffast-math` make opt to IEEE floating point standard will cause incorrect result.

### Software Optimizations

* Software unrolling and register reuse
* Unroll innermost loop, and load a common value in outer loop to register
* avoid repeatedly fetched from L1 or L2 caches.
* Avoiding pointer arithmetic in arrays
* In array: `c[10]` is better than `*(c + 10)`
* c[10] can be execute in one LOAD instructions
* Avoiding inequality comparsions
* BRNZ(Branch if not ZERO) extremely fast
* replace inequality based for-loop to equality based for-loop
* Interspacing add-multiply operations
* add, multiply performed in different processing units

### Copy Optimizations

在矩陣乘法當中，乘法是以行（column）乘以列（row），且在此假設矩陣以 row-major 的方式儲存，那麼在 Matrix 的大小是 $2^N$ 的時候，column 中每一個元素的地址是被用 $2^N$ 去切開的。而也因為 L1 Cache 使用 direct mapped cache，這會導致大量的 Cache Misses。

「remedy」則是一個解決此問題的技術，在乘法運算開始之前，將第一個矩陣存成 Row-major 的格式，而第二個矩陣存成 Column-major 的格式，這種作法就達成了空間局域性（Space Locality）

### L2 Cache blocking optimizations

把 L2 Cache 也加進來算，這樣可以存放更多 Matrix 的資料

## 閱讀資料
[Optimizing matrix multiplication](http://networks.cs.ucdavis.edu/~amitabha/optimizingMatrixMultiplication.pdf)