# Plonk 學習
* "證明"的目的很重要,必須要了解到底證明什麼。
ZKP有兩個角色, 一個是prover, 一個verifier,
如果要編寫prover, 有兩點要留意,第一是要產生一個有效的proof, 第二是要注意在產生proof時,有沒有暴露了一些不想公開的訊息。
如果要編寫verifier,要關注檢查的proof是不是有效的,能否滿足成為有效證明的條件。
prover要用最少的資源去證明一件事,verifier要用最少的資源去驗證一件事。
當完成一組代碼後,就算順利完成編譯,也不算是完全沒有bug的。因為代碼的完整性是不能忽視,需要經過測試,不過惡意的prover有很多種,在測試上是存在很大難度,難以完全進行所有測試。畢竟技術也在進步,有時候新的技術可能會欺騙到verifier。
所以在設計上,最重要的要考慮到自己寫的verifier如何不被惡意prover欺騙。
一個協議需要關注以下三部分:
1. 完整性(completeness)
能否驗證所有為真的證明
2. 可靠性(soundness)
當證明是真的,就會通過驗證
3. 零知識(Zero-knowledge)
保護個人隱私
在prover與verifier之間要有大量交互,在有足夠多的交互下,才可以進一步減低作弊的風險。
真的證明能通過驗證,是其中一項條件,不代表這就是完整的。
如果要是假的證明又能通過驗證,這就雖然通過完整性,但就欠缺可靠性。所以兩者需要同時
如果不能區分假的證明,這就雖然通過可靠性,但就欠缺完整性。
所以兩者需要同時為真,才可以做到有效的驗證。
基於Non-interactive zero-knowledge proof ,用戶可以直接生成proof,然後發送到區塊鏈上進行驗證。
從而加快驗證效率
透過Fiat-Shamir transformation,可以實現Non-interactive zero-knowledge proof,
令public coin protocol變成Non-interactive proof。
public coin protocol 可以讓誠實的驗證點發出隨機的coin(可以理解為隨機數)作為訊息,然後由prover產生一個proof。
不過發出隨機的coin的動作不一定由verifier負責,可以由其他人負責。
所以可以引入random oracle(例如是 cryptographic hash function)來生成隨機數,然後由prover產生一個proof,再直接發送給verifier(on-chain)。因此,也減少了verifier的工作量。

commitment 有以下特性:
- O(1) size
- Binding, 當commitment出現,其數值就不能被修改。保證其他人拿到你的commitment也不可以再改它。
- Hiding, 當數值不公開,就不能被發現。不被人知道你的輸入資料, 每次生成的commitment都不同。
Plonk具有 commit-and-prove的特性,
commitment 有什麼種類?
1. hash
2. merkle-tree
3. pedersen commitment
* 當然是還有其他的,我會繼續去深入了解。
why zkSNARK?
1. 可以實現verifier on-chain
2. recursive proof: 可以進一步優化計算的compression及可以做到不同組合的計算效果.
why Plonk?
1. 是一個universal trust setup (KZG10)
2. Proving O(nlogn), Verifier O(logn), Proof-size O(1)
Plonk 的組成部分是 arithematic + polynomial IOP。
circut:
門是屬於 Polynomial Gates。
當Circut經過計算之後會產出一堆polynomial。
polynomial會交給polynomial IOP
polynomial commitment
例子 : KZG10, IPM, FRI
這裡不是單單驗證一件事,而是驗證整個多項式。
#### 參考文章:
1. Fiat-Shamir transformation
* https://www.zkdocs.com/docs/zkdocs/protocol-primitives/fiat-shamir/
2. zkSNARK是如何組成的 — 1
* https://medium.com/swf-lab/zksnark%E6%98%AF%E5%A6%82%E4%BD%95%E7%B5%84%E6%88%90%E7%9A%84-1-2c6a474bcb06
3. Zero Knowledge Proofs: Example with Pedersen Commitments in Monero
* https://medium.com/coinmonks/zero-knowledge-proofs-um-what-a092f0ee9f28
4. Understanding KZG10 Polynomial Commitments
* https://taoa.io/posts/Understanding-KZG10-Polynomial-Commitments
5. Recursive zkSNARKs: Exploring New Territory
* https://0xparc.org/blog/groth16-recursion
## PLONK算術化
https://www.youtube.com/watch?v=L3qMBzPgfWY
Plonkish算术化是PLONK證明系統特有的算术化
在Plonkish出現之前,其實主流的電路表達形式都是為RICS,而這表達形式已被多個零知識證明算法所使用,包括Groth16。
學習了加法門和乘法門在運算符中的區分。
* 以下是一個電路例子:

1. 有3個門、6個輸入及1個輸出。
2. 滿足了3個約束。
* X1 + X2 = X6
* X3 * X4 = X5
* X6 * X5 = OUT
* 以下是一個矩陣W表格:
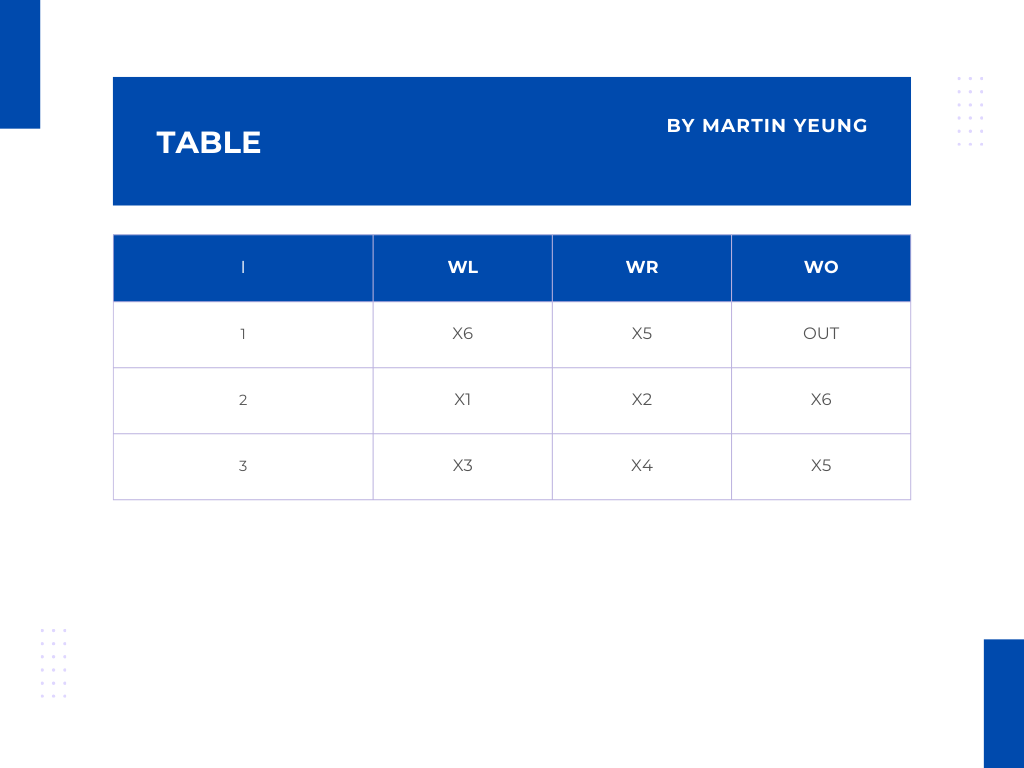
* 在表格中的第1行是各欄的標題,i是指門、 WL是指左輸入、WR是指右輸入及WO是指輸出。
第1列是指第1個門,會看到X6是指左輸入、X5是指右輸入及OUT是指輸出。
第2列是指第2個門,會看到X1是指左輸入、X2是指右輸入及X6是指輸出。
第3列是指第3個門,會看到X3是指左輸入、X4是指右輸入及X5是指輸出。
* 為了能對加法門和乘法門進行區分,會以這個矩陣Q表格作展示:
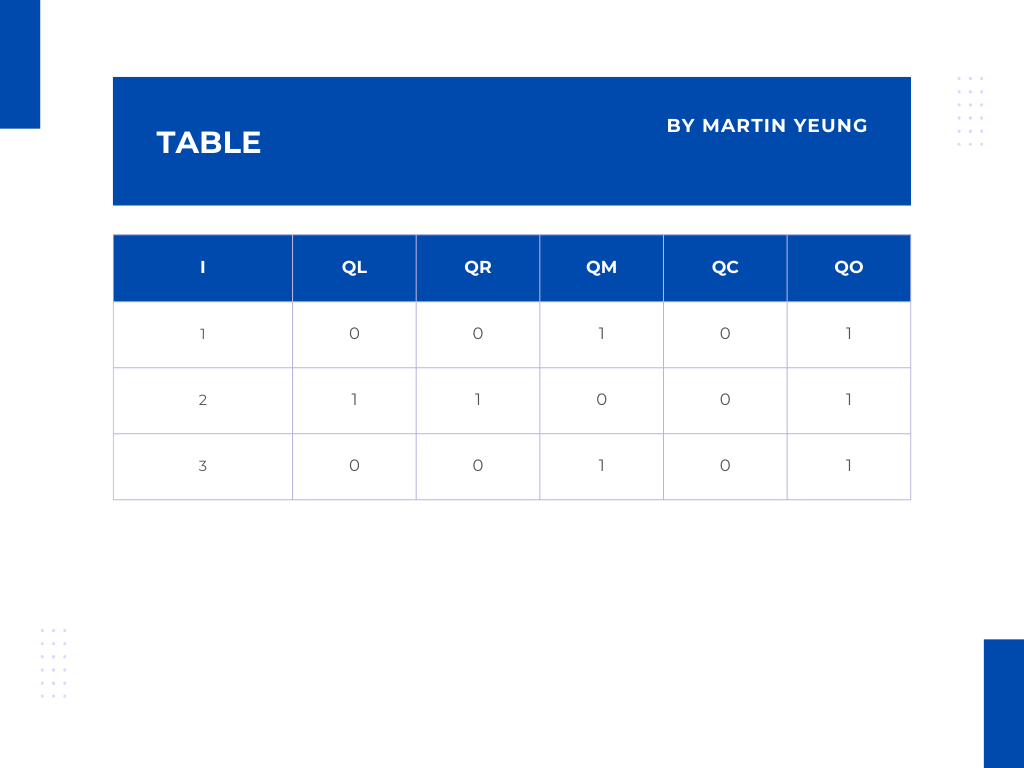
* QL 和 QR 來表示加法門的輸入
* QL 是指左輸入
* QR 是指右輸入
* QM 表示乘法門
* QC 表示常量的數值
* QO 表示輸出
### 認識複製約束
* 由於在矩陣W表格中,可以看到第1個門的左轉入W6不一定等於第2個門的輸出X6。所以需要加入複製約束來確保第1個門的左轉入W6一定等於第2個門的輸出X6。也可以看到加入複製約束可以讓輸出的值會等於另一輸入的值,從入讓事出和輸入形成一種關連,而不是各自各的約束。
### 插值 (拉格朗日插值)
拉格朗日插值法可以找到一個多項式,其恰好在各個觀測的點取到觀測到的值。
有了一個多項式,可以便利驗證。
### 例子解說
矩陣W表格可以說是Prover需要準備的資料,當準備好之後,可以進行編譯。
完成後編譯,可以將結果發送給Verifier。
現在在矩陣W加多一項約束,約束是最終輸出是99。
因此,新增一條約束後的矩陣W表格會是這個:

* 由於只是新增輸出一項約束,不會影響算術門的數量及輸入的值。
假設參數:
* 第1列是指第1個門,左輸入X6是3、右輸入X5是33及OUT輸出是99。
* 第2列是指第2個門,左輸入X1是1、右輸入X2是2及X6是3。
* 第3列是指第3個門,左輸入X3是3、右輸入X4是11及X5是33。
* 第4列是沒有指向任何門,只是其中一個輸出約束,左輸入是0、右輸入是0及輸出是99。
另外,新增一條約束後的矩陣Q表格會是這個:
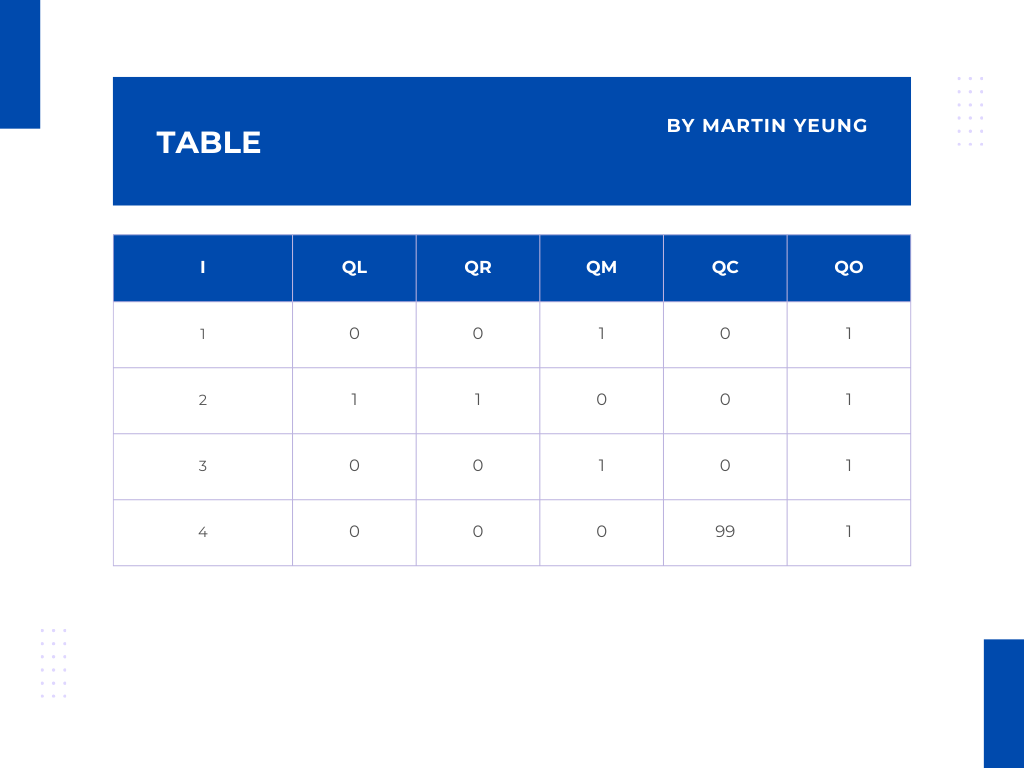
當拉格朗日插值需要滿足QL[0,1,0,0]時,即f(0)=0, f(1)=1, f(2)=0, f(3)=0 .
```math
L_{0}(x) = \frac{(x-1)(x-2)(x-3)}{(0-1)(0-2)(0-3)} = 84*[x^3 - 6*x^2 + 11x -6] = 84x^3 + x^2 + 15x + 1
```
```math
L_{1}(x) = \frac{(x)(x-2)(x-3)}{(1-0)(1-2)(1-3)} = 51*[x^3 - 5*x^2 + 6x] = 51x^3 + 48x^2 + 3x
```
```math
L_{2}(x) = \frac{(x)(x-1)(x-3)}{(2-0)(2-1)(2-3)} = 50*[x^3 - 2*x^2 + 49x] = 50x^3 + 2x^2 + 49x
```
```math
L_{3}(x) = \frac{(x)(x-1)(x-2)}{(3-0)(3-1)(3-2)} = 17x^3 + 50x^2 + 34x
```
* 最終的拉格朗日插值式為:
```math
P(x) = 0*L_{0}(x) + 1*L_{1}(x) + 0*L_{2}(x) + 0*L_{3}(x) = 51x^3 + 48x^2 + 3x
```
當拉格朗日插值需要滿足WL[3,1,3,0]時,即f(0)=3, f(1)=1, f(2)=3, f(3)=0 .
* 最終的拉格朗日插值式為:
```math
P(x) = 3*L_{0}(x) + 1*L_{1}(x) + 3*L_{2}(x) + 0*L_{3}(x) = 49x^3 + 57x^2 + 94x + 3
```
換言之,要滿足QL[3,1,3,0],就必須在f(0)=3, f(1)=1, f(2)=3, f(3)=0時通過以上多項式。
## PLONK中的多項式
* 透過多項式編碼,可以將多個約束轉換成一個約束。
### 多項式的概率檢查
* 要做多項式的概率檢查,需要有2個多項式,而且同為2個次數不多於d的多項式。Verifier只要進行一次多項式隨機挑戰就可以。這是Schwartz-Zippel定理。
* 因為可以進一步地去使用多項式承諾(Polynomial Commitment),讓Prover負責計算x在某一任意地方的值,然後發送證明,這樣Verifier的工作量可以減少。
* 假設要驗證向量a + 向量b是否等於向量c:
可以先把向量編碼成多項式(系數編碼方式)
```math
a(x) = a_{0} + a_{1}(x) + a_{2}(x^2) + ... + a_{n-1}(x^n-1)
```
```math
b(x) = b_{0} + b_{1}(x) + b_{2}(x^2) + ... + b_{n-1}(x^n-1)
```
```math
c(x) = c_{0} + c_{1}(x) + c_{2}(x^2) + ... + c_{n-1}(x^n-1)
```
Verifier 只需要給出一個隨機挑戰值(任意值) ζ∈F
```math
a(ζ) + b(ζ) = c(ζ)
```
如果成功證明到以上公式,則向量a + 向量b是等於向量c。
不過當要驗證向量a乘向量b是否等於向量c,就需要用拉格朗日插值的編碼方式,經轉換之後如下:
```math
a(X)⋅b(X)=c(X),∀X∈H
```
但在這公式,Verifier需要挑戰多次才可以縮小出錯概率。
因此,需要更高效的方法來進行檢測,目標是只用一次就可以檢查出Prover是否存在作弊行為。
```math
a(X)⋅b(X)−c(X)=q(X)⋅z H(X),∀X∈F
```
在公式上可以看到a(X)⋅b(X)−c(X)會等於0,所以q(X)⋅zH(X)也會等於0。
換言之,在X∈H的條件下,H會是a(X)⋅b(X)−c(X)的根集合。因為X必須要使到a(X)⋅b(X)−c(X)等於0。
另外,a(X)⋅b(X)−c(X)可以被多項式zH(X)整除,並得到一個商多項式q(X)。所以只要讓Prover計算出q(X),就可以使到Verifier的工作量減少至只需進行一次隨機檢測就可知道a(X)⋅b(X)−c(X)在X∈H的條件下是否等於0。而Verifier 計算 zH(ζ) 需要 O(n) 的計算量。
### 單位根 Roots of Unity
以單位根作為 H,這可使到zH(ζ)的計算量會減少至O(logn)。
## PLONK中的置換證明
Plonk 的複製約束是通過置換證明(Permutation Argument)來實現。
在這個矩陣W表格中(加入位置標示):

可以看到,WL1 = WO2, WR1 = WO3, WO1 = WO4 。而置換證明可以通過轉換它們的位置,然後再證明置換後的新矩陣是等於矩陣W。
### 基礎協議 - Grand Product Argument
由於進行多項式編碼,所以會把多個單乘法壓縮成單次乘法的驗證。
這裡可以理解成將多個約束壓縮在一起,轉換成1個可驗證的多項式。
* 引入一個輔助向量r
```math
r_{0} = 1
```
* r是每一個對上計算的結果(Accumulator)
```math
r_{k+1} = q_{k}*r_{k}
```
假設現在有3個約束,第1個約束的起始值是1,公式是:
```math
L_{0}*(r(X)-1) = 0 ,∀X∈H
```
第2個約束(遞歸的乘法關系)的公式是:
```math
q(X)*r(X) = r(w.X) ,∀X∈H∖{ω-^1}
```
第3個約束 - 為最後結果是:
```math
r_{n-1} = p ,∀X∈H
```
第3個約束的公式是:
```math
L_{n-1}*(r(X)-r_{n-1}) = 0 ,∀X∈H
```
利用遞歸的乘法關系:
```math
q(X)*r(X) = r(w.X) ,∀X∈H
```
最後得出可以驗證的多項式:(以下是相關步驟)
```math
q(X)*r(X) - r(w.X) = 0 ,∀X∈H
```
```math
L_{0}(X)*(r(X) - 1) + q(X)*r(X) - r(w.X) = 0 ,∀X∈H
```
```math
L_{0}(X)*(r(X) - 1) + (α*q(X)*r(X) - r(w.X)) = 0 ,∀X∈H
```
```math
L_{0}(X)*(r(X) - 1) + α*(q(X)*r(X) - r(w.X)) = h(X)*Z_{H}(X) ,∀X∈H
```
當中α是一個隨機數,h(X)是商多項式,
```math
Z_{H}(X)是(X-1)(X-W)...(X-W^{n-1})
```
### 如何利用連乘證明來實現Multiset等價證明(Multiset Equality Argument)
假設向量 {qi} 為一個多項式 q(X) 的根集合,即對向量中的任何一個元素qi,都滿足q(ri)=0。這個多項式可以定義為:
```math
q(X) = (X - q_{0})(X - q_{1})...(X - q_{n-1})
```
如果有另一多項式p(X)與q(x)相同,則會具有相同的根集合。
可以利用 Schwartz-Zippel 定理做檢驗,只要Verifier輸入一個隨機數 γ,Prover就可以通過下面的公式以證明向量 {pi} 和 {qi} 是在多重集合上是等價。
```math
\prod_{i\in[n]}(γ-p_{i}) = \prod_{i\in[n]}(γ-q_{i})
```
然後,再使用連乘證明完成驗證,通過加入輔助向量,轉換成可以驗證的多項式。在目前例子,兩個連乘公式可以轉換成為一個連乘公式:
```math
\prod_{i\in[n]}\frac{(γ-p_{i})}{(γ-q_{i})} = 1
```
### 如何證明Multiset與置換證明(Permutation Argument)的關係
首先,要Prover證明兩個向量是滿足奇偶位置互換的置換情況。
```math
\vec{a} = (a_{0}, a_{1}, a_{2}, ..., a_{n-1}, a_{n})
```
```math
\vec{b} = (b_{0}, b_{1}, b_{2}, ..., b_{n-1}, b_{n})
```
可以運用多項式編碼把向量轉換成多項式,同時加入位置向置來表示奇偶位置互換。
```math
\vec{i} = (0, 1, 2, 3, ..., n-1, n)
```
```math
σ = (0, 1, 3, 2, ..., n, n-1)
```
兩個向量以表格形式列出一部分:

之後,再整理一下,將表格中的左面和右面分成2組如下:
```math
a^{\prime} = (a_{i}, i) , b^{\prime} = (b_{i}, σ(i))
```
```math
(a_{0}, 0) , (b_{0} = a_{1}, 1)
```
```math
(a_{1}, 1) , (b_{1} = a_{0}, 0)
```
```math
\vdots , \vdots
```
```math
(a_{n-1}, n-1) , (b_{n-1} = a_{n}, n)
```
```math
(a_{n}, n) , (b_{n} = a_{n-1}, n-1)
```
根據以上情況,如果2個向量(a, b)滿足奇偶位置互換的置換情況,則以上2個向量(a', b')也會滿足Multiset等價的關系。
若要轉換為一個多項式(或一個新的向量),可以加入一個隨機數β,結果如下:
```math
a_{i}^{\prime} = (a_{i} + β*i) , b_{i}^{\prime} = (b_{i} + β*σ(i))
```
```math
(a_{0} + β*0) , (b_{0} + β*1)
```
```math
(a_{1} + β*1) , (b_{1} + β*0)
```
```math
\vdots , \vdots
```
```math
(a_{n-1} + β*(n-1)) , (b_{n-1} + β*(n))
```
```math
(a_{n} + β*(n)) , (b_{n} + β*(n-1))
```
## 算術約束與複製約束
### 向量的複製約束
一個向量中,可以證明多個不同位置上的向量元素相等,例子如下:
```math
\vec{a}= (a_{0} + a_{1} + a_{2} + a_{3})
```
如果要證明
```math
a_{0} = a_{2}
```
可以將它們的位置對調,以σ 表示位置向量:
```math
\vec{a}_{σ} 為置換後的向量
```
```math
σ = (2, 1, 0, 3), \vec{a}_{σ} = (a_{2} + a_{1} + a_{0} + a_{3})
```
只要Prover證明到置換前的向量和置換後的向量相等,就表示:
```math
a_{0} = a_{2} 是正確的
```
### 向量(多個)的複製約束
* 以下會以例子說明整個流程:
選用矩陣W表格,同時加入一個輸出的約束。

會留意到有些地方的值是相等的,包括:
```math
w_{a,1} = w_{c,2}, w_{b,1} = w_{c,3}, w_{c,0} = w_{c,1}
```
* 對表格中的三列向量用三個置換向量統一地進行位置編碼,結果如下:

置換後的向量為:
```math
σ_{a} , σ_{b} , σ_{c}
```

因此,現在會有2個向量,分別是置換前的向量及置換後的向量。為了進行下一步驗證,需要利用一個隨機數β來進行向量合併。
之後再利用另一個隨機數γ配合連乘以獲得2個向量的Multisets。
置換前的向量:
```math
f_{i} = (w_{a,i} + β*id_{a,i} + γ)(w_{b,i} + β*id_{b,i} + γ)(w_{c,i} + β*id_{c,i} + γ)
```
置換後的向量:
```math
g_{i} = (w^{\prime}_{a,i} + β*σ_{a,i} + γ)(w^{\prime}_{b,i} + β*σ_{b,i} + γ)(w^{\prime}_{c,i} + β*σ_{c,i} + γ)
```
進一步演示 - 置換前的向量:
```math
f_{0} = (w_{a,0} + β*0 + γ)(w_{b,0} + β*4 + γ)(w_{c,0} + β*8 + γ)
```
```math
f_{1} = (w_{a,1} + β*1 + γ)(w_{b,1} + β*5 + γ)(w_{c,1} + β*9 + γ)
```
```math
f_{2} = (w_{a,2} + β*2 + γ)(w_{b,2} + β*6 + γ)(w_{c,2} + β*10 + γ)
```
```math
f_{3} = (w_{a,3} + β*3 + γ)(w_{b,3} + β*7 + γ)(w_{c,3} + β*11 + γ)
```
進一步演示 - 置換後的向量:
```math
g_{0} = (w^{\prime}_{a,0} + β*0 + γ)(w^{\prime}_{b,0} + β*4 + γ)(w^{\prime}_{c,0} + β*9 + γ)
```
```math
g_{1} = (w^{\prime}_{a,1} + β*10 + γ)(w^{\prime}_{b,1} + β*11 + γ)(w^{\prime}_{c,1} + β*8 + γ)
```
```math
g_{2} = (w^{\prime}_{a,2} + β*2 + γ)(w^{\prime}_{b,2} + β*6 + γ)(w^{\prime}_{c,2} + β*1 + γ)
```
```math
g_{3} = (w^{\prime}_{a,3} + β*3 + γ)(w^{\prime}_{b,3} + β*7 + γ)(w^{\prime}_{c,3} + β*5 + γ)
```
由於
```math
w_{a,1} = w^{\prime}_{c,2}
```
```math
w_{c,2} = w^{\prime}_{a,1}
```
所以:
```math
(w_{a,1} + β*1 + γ) = (w^{\prime}_{c,2} + β*1 + γ)
```
```math
(w_{c,2} + β*10 + γ) = (w^{\prime}_{a,1} + β*10 + γ)
```
換言之:
```math
\prod_{x\in H}f(X) = \prod_{i\in H}g(X)
```
```math
\prod_{x\in H}\frac{f(X)}{g(X)}
```
現在再利用新的向量z,以表示連乘計算的一系列中的過程。
需假設:
```math
Z_{0} = 1, Z_{i+1} = Z_{i}*\frac{f(i)}{g(i)}
```
Prover可以計算出以下的值:

```math
如果\vec{f} = \vec{g},則Z_{N}會等於1
```
所以:
```math
Z_{N} = Z_{0} = 1
```
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet