:dart: W12 - Logistic Regression
===

<!-- ## Table of Content
[Toc] -->

## 名字：靖涵
### Logistic Regression

- **linear regression**
計算 p-value 看變數之間有沒有顯著性
再計算 R^2 看變數之間的關聯性有多大
可以用一個變數去預測出另一個變數
變數以 least square 符合線性分佈，即找出最小的殘差平方和(minimizes the sum of the squares of these residuals)

- **multiple regression**
和 linear regression 一樣都計算 p-value 和 R^2
另外還可以用兩個變數去預測出第三個變數

- **logistic regression**
不同於前面的 regression 僅是預測出連續值(continuous)，logistic regression 使用 S shaped logistic function，即可把預測出的數值壓在 0 到 1 之間，進一步去設立分界，以預測是 0/1 哪一個類別(classification)。這樣可以提供新樣本分類機率讓 logistic regression 變成之後 machine learning 的基礎。


- **Multivariable Logistic Regression（多變量邏輯回歸）**
和一般 Logistic Regression 差在自變量的數量， 在Multivariable Logistic Regression 中會使用多個自變量預測目標變量的機率，但一般的 Logistic Regression 只有單一個變量。

[Reference_LogisticRegression_1](https://www.youtube.com/watch?v=yIYKR4sgzI8&list=PLblh5JKOoLUKxzEP5HA2d-Li7IJkHfXSe)
[Reference_LogisticRegression_2](https://towardsdatascience.com/introduction-to-logistic-regression-66248243c148)
### Maximum Likelihood Estimation (MLE)

- logistic regression 的計算也不同於 linear regression 計算 least squares 和 R^2，而是使用 maximum likelihood。
- 即選定一個 curve 然後計算每一個 data 在這個 curve 情況下的 likelihood，最後再把所有 data 的 likelihood 相乘，計算整個資料集的聯合機率(joint probability)；接著再移動 curve 然後重複計算一次，一直重複，然後最後選定會有 maximum likelihood 的 curve。
- MLE 是估計模型參數的方法，為了能最好解釋觀察到的資料的模型參數，所以要透過已經可以觀察到的樣本資訊推導出背後能產出這樣樣本結果的模型參數（likelihood 概念： 不知道母數有多大，但從現在既有資源去推估）。所以可以說是要找到可以使 likelihood 最高的一組模型參數，也就是 Maximum Likelihood。

[Reference_MaximumLikelihood_1](https://medium.com/qiubingcheng/%E6%9C%80%E5%A4%A7%E6%A6%82%E4%BC%BC%E4%BC%B0%E8%A8%88-maximum-likelihood-estimation-mle-78a281d5f1d)
[Reference_MaximumLikelihood_2](https://www.youtube.com/watch?v=XepXtl9YKwc)

---

## 名字：俞辰
### Logistic Regression
邏輯迴歸是一種資料分析技術，使用數學來尋找兩個資料要素之間的關係。然後，根據其中一個要素預測另一個要素的值。不同於線性回歸是用來預測一個連續的值，邏輯回歸是用來做分類的。此外，以此方式預測得到的結果只能是二元分類，其中結果變數顯示兩個類別（0 和 1）中的一個，無法更細微的預測因變數的實際值。例如，我們透過歷史資料去預測消費者會不會按下購物車中的結帳按鈕、學生會不會通過考試，以及吸菸者會不會得到肺癌等。


羅吉斯回歸用到的對數函數是Sigmoid函數，公式與圖形如下:

邏輯迴歸包括三種基本類型：
* 二進位：二進位輸出是一個變量，其中只有兩種可能的結果。這些結果必須是相互對立且互相排斥的。是否有貓是二進制輸出。
* 多項：多項迴歸可分析有幾種可能結果的問題，只要結果的數量是有限的。例如，它可以根據人口數據，預測房價是否會增加 25%、50%、75% 或 100%，但無法預測房屋的確切價值。
* 序數：是一種特殊類型的多項迴歸，針對其中數字代表排列，而非實際值的問題。例如，您可以使用序數迴歸，來預測調查問題的答案，該問題要求客戶根據數值 (如他們在一年中向您購買的商品數量)，將您的服務評級為「較差」、「一般」、「較好」或「出色」。

[Reference 1](https://aws.amazon.com/tw/what-is/logistic-regression/)
[Reference 2](https://chih-sheng-huang821.medium.com/%E6%A9%9F%E5%99%A8-%E7%B5%B1%E8%A8%88%E5%AD%B8%E7%BF%92-%E7%BE%85%E5%90%89%E6%96%AF%E5%9B%9E%E6%AD%B8-logistic-regression-aff7a830fb5d)

### Correspondence Analysis
對應分析，也稱為倒數平均，是一種有用的數據科學視覺化技術，用於尋找和顯示類別之間的關係。它使用繪製數據的圖表，直觀地顯示兩個或多個數據點的結果。對應分析有助於衡量品牌之間的相似性以及不同特色方面的實力。例如，假設一家公司想要了解不同品牌的飲料對於消費者來說有哪些特色屬性。

假設我們要將對應分析應用於不同品牌的汽水產品，首先我們需要收集各項變數的數據並做出一個二維表如下，行和列上各有一組變數，這裡的兩組變數分別是「品牌」和「屬性」。

在對應分析中，我們想要查看每個單元格的殘差。正殘差向我們表明，該品牌屬性配對的計數遠高於預期，表明存在牢固的關係；相應地，負殘差顯示的值低於預期，表示關係較弱。殘差 R 等於：R = P - E，其中 P 是觀察到的比例，E 是每個像元的預期比例。

觀察到的比例 (P) 等於儲存格中的值除以表中所有值的總和。因此，對於上面的列聯表，總和將為：5 + 7 + 2 + 18 … + 16 = 312。計算後的結果如下表:

接著，我們可以根據觀察到的比例輕鬆計算出比例表中行和列的總和，即行質量和列質量，如下表:

而預期比例（E） 將是我們期望在每個單元格的比例中看到的內容，假設行和列之間沒有關係。我們對單元格的期望值將是該單元格的行質量乘以該單元格的列質量。

現在，我們可以計算殘差 R 表，其中 R = P - E。

取 Squishee 和 Economic 的最大負值 -0.045，我們在這裡的解釋是 Squishee 和 Economic 之間存在負關聯；與我們其他品牌的飲料相比，Squishee 不太可能被視為「經濟」。

[Reference 1](https://www.qualtrics.com/eng/correspondence-analysis-what-is-it-and-how-can-i-use-it-to-measure-my-brand-part-1-of-2/)
[Reference 2](https://www.tibco.com/glossary/what-is-correspondence-analysis)

---

## 名字：予茜
### 羅吉斯回歸(logistic regression)
**特色**：
1. 適用於分類問題，因變數必須為**類別**變數，自變數可為類別或連續變數。
2. 線性迴歸中的依變數(Y)通常為連續型變數，但羅吉斯迴歸的依變數主要為**類別**變數，特別是分成兩類的變數(例如：是或否、有或無等）。
3. 若類別只有兩種，則為二元邏輯式迴歸(Binary logistic regression)，若是類別超過三個以上則為 Polytomous logistic regression，是更複雜的模型。
4. 以勝算比(odds ratio)來計算，勝算即**事件成功機率與失敗機率的比值**。

**假設**：
1. 在羅吉斯回歸中，自變數對依變數的影響是以**指數**的方式做變動，因此數據不需要常態分配的假設。

2. 依變數Y為二元變數，p為其成功的機率，受自變數ｘ所影響，則p與ｘ之關係如下：
Ｙ事件成功的機率：
Ｙ事件失敗的機率：
p的值會介於0~1之間，當p接近0時表示Y成功的機會很小，接近1時則表示成功的機會很大。

**公式**：對勝算比取自然對數(ln)得之。
係數值( )→當值增加一單位時勝算的改變量(Δ odds)。

當 Δ odds > 1，表示當Xi 增加時，事件Y 的勝算比提高
當 Δ odds < 1，表示當Xi 增加時，事件Y 的勝算比降低
＊Δ odds 又稱為OR值。

**例子**：一個班上有20名學生，各自花費0~6小時準備考試，請問學生不同的學習時數如何影響通過考試的機率？

依變數(Y)：通過為1，不通過為0
自變數(X)：學習的時間(0~6)


[picture](https://www.yongxi-stat.com/logistic-regression/)
[reference](https://www.yongxi-stat.com/logistic-regression/)
[reference](https://zh.wikipedia.org/zh-tw/邏輯斯諦迴歸)

---
## 名字：植棻

### Regression Analysis 迴歸分析
迴歸分析的目的是了解兩個或多個變數間==是否相關、相關方向與強度==。期望瞭解自變數的變化，對於依變數產生的改變量。而透過回歸分析，可以由給出的自變數，估計依變數的條件期望值。（做預測）

**一些關鍵字：**
- 欲預測、推估或估計的變數：
- 依變數、因變數、應變數(response variable; regressand)
- 相依變數(dependent variable)
- 解釋變數(explained variable)
- 欲操作、操縱的變數：
- 自變數、獨立變數(independent variable)
- 預測變數、解釋變數(explanatory variable; regressor)

**迴歸分析的種類：**
- **線性**
- 簡單線性迴歸 (Simple linear regression)：一個自變數，一個依變數
- 多元迴歸/複迴歸 (Multiple regression)：多個自變數，一個依變數
- 對數線性迴歸 (Log-linear regression)：將自變數跟依變數的數值都取對數，再進行線性回歸。所以依據依變數的數量，會有**對數簡單回歸**或是**對數複回歸**
- 多變量迴歸分析 (Multi-variable regression)：多個自變數預測數個依變數

- **非線性**
- 對數機率回歸 (Logistic Regression)
- 偏回歸 (Partial Regression)

### Linear Regression

只有一個自變數跟依變數，兩者的關係趨近於比例關係（線性關係、直線關係）自變數與依變數之間的關係可以分為：
- 正向關係
- 負向關係
- 沒有(無)關係

例如：想要了解餐廳的行銷費用（自變數$X$）與餐廳的營業額（依變數$Y$）的關係。

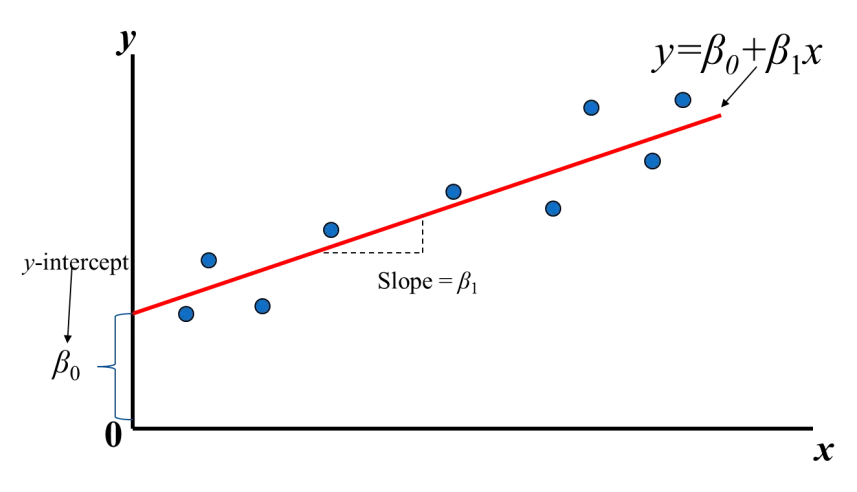
==簡單線性回歸公式：$ŷi =β0+β1xi，i=1, …,n$==
回歸分析就只是在找 $β0$ 和 $β1$ ，所以會將一組資料的每個點$(xi, yi), i=1, …,n$ 帶到回歸公式內
$ŷi$ 為預估出來的餐廳的營業額，和真實資料還是會有誤差(error)或稱為殘差(Residual)：$εi = yi — ŷi$ ，殘差越小表示預測的越好

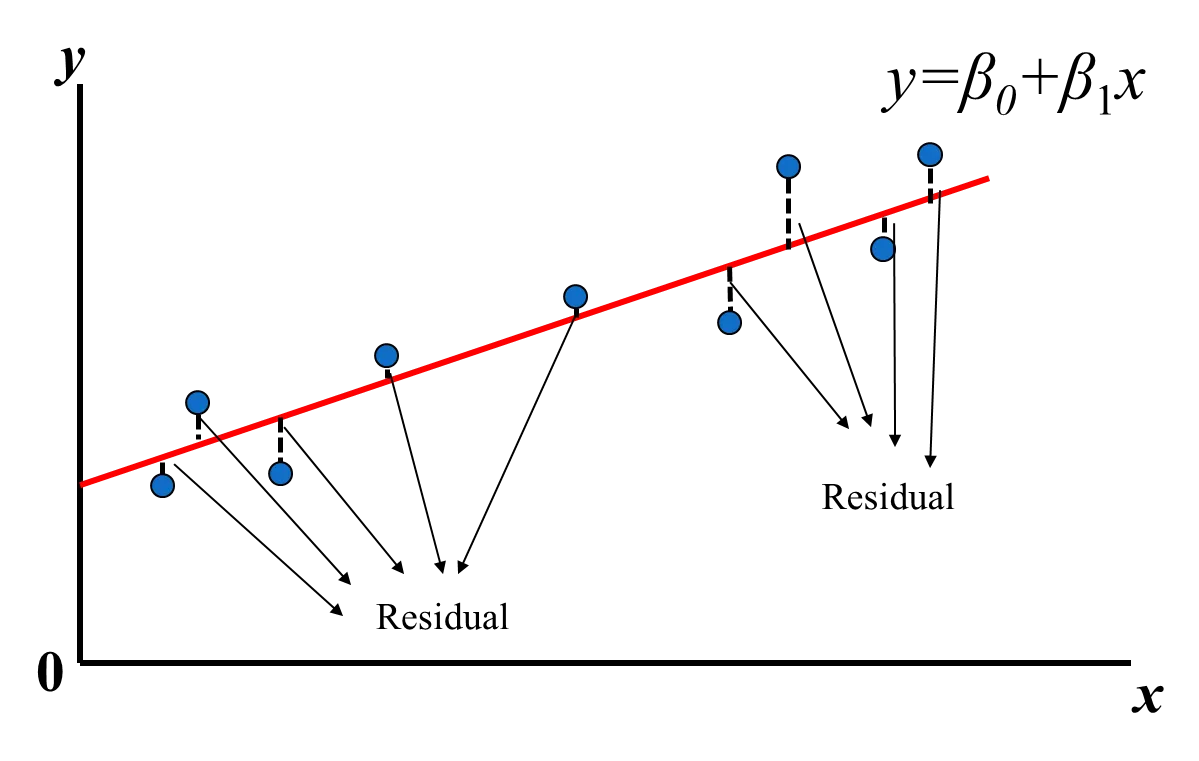
[ref_1](https://chih-sheng-huang821.medium.com/線性回歸-linear-regression-3a271a7453e)
[ref_2](http://www2.nkust.edu.tw/~tsungo/Publish/14%20Simple%20linear%20regression%20analysis.pdf)

### Logistic Regression

邏輯回歸是一個分類模型，通常依變數會是類別變數(categorical variable)且是二元類別
自變數對依變數的影響是以指數的方式做變動，因此不需要常態分配的假設。

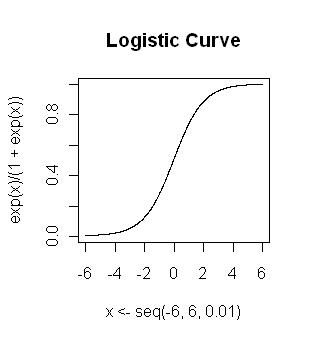
邏輯回歸會找一個機率 (posterior probability)，機率會透過一個 sigmoid function（也稱為logistic function）將輸出轉換成 0~1 的值。

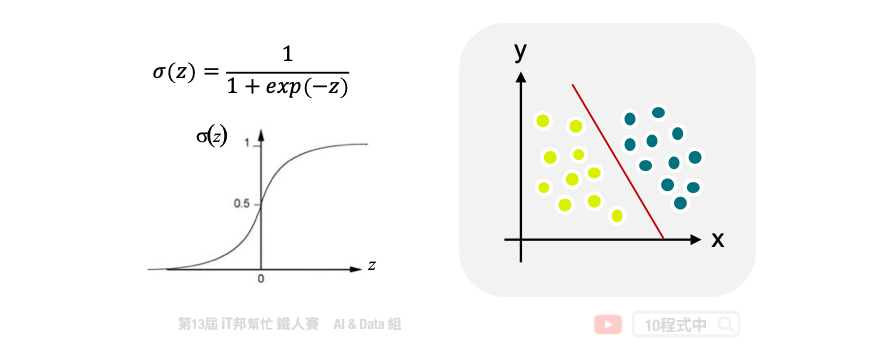
當機率 $P(C1|x)>0.5$ 時則判斷為 Class 1，反之機率 $P(C1|x)<0.5$ 則判斷為 Class 2
$x$ 為輸入特徵，而 $w$ 與 $b$ 分別為權重 (weight)與偏權值 (bias)

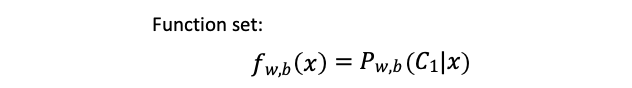
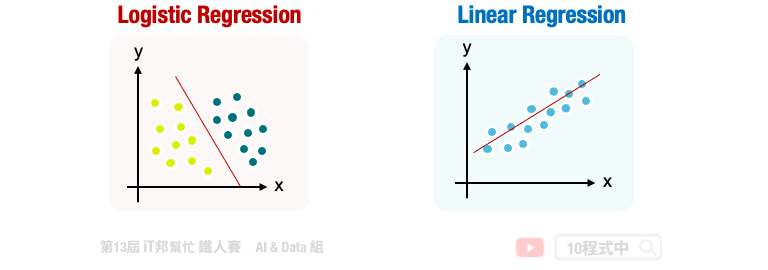
邏輯回歸的目標是找到一條直線可以將資料做分類（如左圖）
右圖則是線性回歸，目標是想找一條直線可以逼近真實的資料，以進行預測。


[ref_1](https://www.yongxi-stat.com/logistic-regression/)
[ref_2](https://medium.com/jameslearningnote/資料分析-機器學習-第3-3講-線性分類-邏輯斯回歸-logistic-regression-介紹-a1a5f47017e5)
[ref_3](https://ithelp.ithome.com.tw/m/articles/10269006)

---
## 名字：瓈萱
### 邏輯斯回歸 logistic regression

回歸分析的一種，主要是來看依變數（dependent variable)和自變數(independent variable)之間的關係，可以預測二元變量（0或1,0 可以想成事件沒發生，1 表示事件發生）並估計1的發生概率。
比如說想要知道什麼因素會影響感然疾病的發生，0代表沒有患有疾病，1代表患有疾病，變數像是年齡、性別、有沒有抽菸等就可以被檢測跟患有疾病的事件有沒有相關，換句話說，考量到上述的變量，這個人患有疾病的可能性有多大。


有關邏輯回歸的幾個特點：
* 是一種監督式學習
* 大多數用來做分類任務（結果只會是0或1 ex. 是/否)
* 依變數是類別變數
#### Multinomial logistic regression
當依賴變數只有兩類（例如男性、女性）時，就會使用常用的二元邏輯回歸分析。但是，如果依賴變數有超過兩類，例如要預測一個人上班會選擇什麼樣的交通工具（汽車、公共交通、自行車），則必須使用多元邏輯分析
#### 邏輯斯回歸和線性回歸的差別
- 一般線性回歸的目的是希望來找一條線，資料點能越靠近那條線越好，而邏輯斯回歸則是希望找到一條線能讓資料分成兩類的線。


- 一般線性迴歸的迴歸係數（regression coefficient）的解釋是「當自變項增加一個單位，依變項會因此增加多少單位」，但是在Logistic regression中的迴歸係數解釋為「當自變項增加一個單位，依變項1相對依變項0的機率會增加幾倍 （就是這變數的改變會不會造成依變數也因此改變 例如：性別如果從男生變成女生的話，患病機率（1的機率）會不會因此提升？）
- 在線性回歸中，如果一個自變量與因變量之間具有強烈的相關性，那個自變量就會被認定是好的。而在邏輯回歸中，如果一個自變量能夠強烈影響到依變量的不同，則該自變量被認為是“好”的。
- 線性回歸的依變數必須要是連續性變數，羅基斯回歸的依變數則是可以是類別變數
[reference](https://ithelp.ithome.com.tw/articles/10289837)
[reference](https://blog.gopenai.com/linear-and-logistic-regression-same-regression-but-different-purpose-f6ff5f93b7ef)
[reference](https://dasanlin888.pixnet.net/blog/post/34468457)
### 對應分析 Correspondence Analysis
一種統計方法，用於分析兩個或多個分類變數之間的關係。它是一種資料視覺化技術，目的是在尋找不同變數類別之間的**模式**和**關聯**。
- 通常使用在市場、商品分析等
- 優點：可以以圖形化的方式，能夠將幾組看不出任何聯繫的數據，通過視覺上可以接受的定點陣圖展現出來。他的目的不是在檢視資料是否適合研究者設定的理論模型，而是單純的呈現資料本身的結構。
[reference](https://www.jianshu.com/p/8f1aa3770c61)
---

## 名字：孟桁
### logistic regression
They can be applied in predicting binary outcomes for classification tasks like decision tree models, though the statistics in this model present the probability of an outcome, not statistical classification. Logistic regression is also less ideal if there are outliers, compared to decision trees.

### cross-tabulation
Basically data tables that record relationships between multiple variables in a row and column format.

---
## 名字：喻璞

### Multivariate Logistic Regression
#### Multivariate model
用於具有一個以上的結果（例如，重複測量）和多個獨立變數的分析。[ref](https://academic.oup.com/ntr/article/23/8/1446/5812038)

> Multivariable model: 用於具有一個結果（x/dependent variables/因變量）和多個自變量（y/independent variables/預測變量/解釋變量）的分析

#### Hirota (2022)
本研究應用了 multivariable logistic regressoin，將 語氣變化(mode) 作為因變量，將其他社會語言因素（年齡、性別、地區、教育水平、副詞、動詞類型、動詞體態、人稱和距離）作為自變量。

- 目的：試圖預測陳述語氣和虛擬語氣的出現機率。

邏輯回歸的好處：
1. 目標是使用最簡潔的模型預測個別情況的結果類別
2. 適用於處理不平衡的數據集
3. Logistic回歸允許分析多個預測變量與一個因變量之間的關係。換句話說，Logistic回歸可以預測每個因素的影響程度

#### 複習
- 線性迴歸（linear regression）是連續性的結果變數 / 線性
- 羅吉斯迴歸（logistic regression）具有二分式结果（dichotomous outcome / 非線性
- 存活分析（survival analysis）包含時間結果預測（time to event outcome）

### odds-ratios (ORs) 勝算比
為實驗組中發生結果的勝算（Odds）與對照組中發生結果的勝算，此兩者間的比值就稱為勝算比（OR）。通常用於計算事件的發生率、或特定結果的各種風險因素的大小。

在計算logistic regression時，回歸係數（regression coefficient; b1）代表每單位exposure增加時結果的對數勝算的估計增加量。換句話說，回歸係數的指數函數（$e^{b1}$）代表exposure增加一個單位時相應的勝算比。

#### 算法
各組的勝算 = 研究過程中各組發生某一事件之人數除以沒有發生某一事件之人數。

[ORs.png](https://www.yongxi-stat.com/wp-content/uploads/2022/11/2022-11-1-OddsRatio-P1.jpg.webp)

以上表為例：實驗組中發生結果的勝算= A/B，對照組中發生結果的勝算= C/D，勝算比= (A/B) / (C/D) = AD/BC。

p.s.
當發生此一事件之可能性極低時，則相對危險比（RR）幾近於勝算比（OR）。 [ref1](https://www.yongxi-stat.com/odds-ratio-or-r/)

- OR = 1：暴露不會影響結果的勝算。
- OR > 1：暴露與結果的勝算有較高的關聯性。
- OR < 1：暴露與結果的勝算有較低的關聯性。

#### confidence intervals
- 95%信賴區間（CI）用於估計OR的精確性。
- CI值大表示OR的精確性水平較低，CI值小表示OR的精確性較高。
- CI與p值不同，95%的CI並不報告一個測量的統計顯著性。 [ref2](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2938757/)

#### OR vs RR
##### odds ratio (OR)
可以用在前瞻性研究(prospective study)與回溯性研究(retrospective study)及病例對照研究(Case–control study)，適用範圍較廣。

##### relative risk (RR)
RR不能用在Case–control study，是因為控制組或對照組的比例一改變，RR也會不同，但OR還是一樣。

[ref3](https://chungyizhen.medium.com/%E7%82%BA%E4%BB%80%E9%BA%BC%E9%83%BD%E7%94%A8-%E5%8B%9D%E7%AE%97%E6%AF%94-odds-ratio-or-%E8%80%8C%E4%B8%8D%E6%98%AF-%E7%9B%B8%E5%B0%8D%E9%A2%A8%E9%9A%AA-rr-%E5%91%A2-5c62fe84787c)

### cross-tabulation 交叉表/交叉分析表

交叉表是一種以行列交叉的方式，進行分類彙整的表格，每一行和每一列上至少會有一個**類別變數**，因此在行與列的交叉處便可以對資料進行多種計算。

叉表常用於比較一或數個變數的結果與另一個變數的結果。它可用來分析名目資料，其中變數的名稱和標籤並無特定順序。我們可以透過交叉表檢視資料之間不明顯的關係。交叉分析表也可呈現市場調查研究中一或數個調查問卷問題間的關聯性。

關於兩個變項間的分佈狀況，可以使用交叉表（Cross Table）來檢視其分佈情形。當依變項(應變數/dependent variable/y)是nominal scale（類別變項）時通常採用Chi-square（卡方）檢定。

p.s. 卡方獨立性檢定適用於分析兩組類別變數的關聯性。

#### Example
**員工滿意度**，透過問卷調查訪問員工以下幾點問題：a. 他們工作時感到多快樂; b. 他們打算在工作崗位上待多久; c. 他們在組織任職多久; d. 他們每日工作幾小時（平均時數）

並將結果整理成以下表格：

[crosstab.png](https://prod.smassets.net/assets/content/sm/sites/16/crosstab1-zh-TW.png)

[ref1](https://www.yongxi-stat.com/spss-cross-table/) [ref2](https://zh.surveymonkey.com/mp/what-is-a-crosstab-and-when-to-use/) [ref3](https://myweb.scu.edu.tw/~swlean/cross%20image/cross%20table.htm)

#### 優點
1. 減少分析資料時的混淆：藉由分類將資料集化繁為簡，進而減少產生的錯誤。
2. 更精細的資料點：可以審視一或數個變數間的關係，從而獲得**層次**更精細的洞見。
3. 可操作的洞見：使用交叉分析表來簡化資料集，以利快速比較資料。
4. 清楚解讀：即使沒受過分析訓練的研究專家與團隊成員也能輕鬆檢視和使用。

---

<!-- ## tags, 拜託不要刪除以下 -->
###### tags: `QL2024`

<!-- ---

## 名字：
### 以下如果要用到標題請打三個以上的井字號 -->