:dart: W11 - Markov Model
===

<!-- ## Table of Content
[Toc] -->

## 名字：瓈萱
### Type I Error & Type II Error

統計上用來表示假說檢定中的兩種錯誤
* 虛無假設 H0：希望能證明假設為錯誤的假設 通常是「沒有差異」、「沒有影響」、「沒有效果」的論述 數據上看不到任何特典或差異 ex. 打疫苗不能減少確診機率
* 對立假設 H1：跟虛無假設完全對立的假設 通常是 數據上能看得出有差異、或特點 ex. 打疫苗可以減少確診機率

1. type one error 型一錯誤 （又被稱作是偽陽性錯誤）

如果真相是 ==虛無假設是正確的==，數據應該顯示沒有任何特點、差異，我們卻判斷出數據有某些特點、差異因此拒絕虛無假設，這試型一錯誤

2. type two error 型二錯誤 （又被稱為是偽陰性錯誤）

如果真像是==虛無假設是錯誤的==，數據應該有顯示有某些差異、效果，我們卻判斷數據是沒有差異性的，因此接受虛無假設，這就是型二錯誤

- 舉個🌰：

假設有一袋巧克力，裡面包含了 白巧克力跟黑巧顆粒兩種 想要知道白巧克力跟黑巧克力的分布情況
虛無假設：白巧克力跟黑巧克力的數量是一樣的
對立假設：其中一種巧克力的數量比較多

假設小弟弟用手去撈一把巧克力的結果是白色撈到3顆黑色撈到5顆 因次斷定袋子中一定有某種巧克力比較多，而如果今天真相是兩種巧克力的數量是一樣的，小弟弟就會犯了型ㄧ錯誤。如果小弟弟今天撈到兩顆白巧 兩顆黑巧，因此推斷說袋子中兩種巧克力的量是一樣的，但真實的分佈是白巧比較多，那他就犯了型二錯誤。

#### 統計學用來表達型一、型二錯誤的機率
型一錯誤機率表達方式：alpha（α）＝顯著水準 一設0.05 所以也可以因此解讀成：如果虛無假設成立，還是有 5% 的機率在數據上看以到顯著的結果

型二錯誤的機率表達方式：beta（β）來表示。
也常用 1 - β 來表示「檢定力」 也就是不犯下型二錯誤的「正確率」。
#### 如何降低型一型二錯誤的發生率
降低型一錯誤發生率：可以調整顯著水準（ex. 0.05 改為0.01)
缺點：結果會過於保守

降低型二錯誤的方法：增加樣本數

* 型一錯誤跟型二錯誤之間存在一個反向的關係：當型一錯誤的發生機率越大，型二錯誤發生的機率就越小。

[reference](https://haosquare.com/type-i-error-and-type-ii-error/)
[reference](https://rayhsu005.medium.com/%E4%BB%80%E9%BA%BC%E6%98%AF%E5%9E%8B%E4%B8%80%E9%8C%AF%E8%AA%A4-type-i-error-%E5%92%8C%E5%9E%8B%E4%BA%8C%E9%8C%AF%E8%AA%A4-type-ii-error-ea163eaa182c)

### Markov Models 馬可夫模型

#### 馬可夫鏈（Markov Chain）
討論一個系統內，同類型的事件（不同的狀態）依序發生的機率。假設天氣可以分為兩種 晴天、陰天 那昨天是晴天，今天是陰天的機率跟昨天陰天 今天陰天的機率會不同。這是因為我們相信前面發生的狀態會影響到後面發生的狀態，這種前面的狀態會引響到後面的狀態就是馬可夫鏈。
在馬可夫鏈中，根據機率分布，可以從一個狀態變到另一個狀態（晴天變陰天），也可以保持當前狀態（維持晴天）。而一個事件/狀態到下一個事件/狀態只與現在的事件/狀態有關


圖是代表馬可夫鏈的示意圖
當前事件為E(晴天），下一個可能發生E（晴天）的機率為0.3 可能發生A（陰天）的機率為0.7
當前事件為A（陰天），下一個可能發生E（晴天）的機率為0.4 可能再發生一次A（陰天）的機率為0.6
#### 馬可夫鏈3大核心要素
- 狀態空間 （states space)
已舉的例子來說，天氣的狀態只可能來自狀態A（晴天）、B（陰天）
- 無記憶性（memorylessness)
當期狀態發生的概率只受上期狀態影響（例子中，*今天的天氣* 只受*昨天的天氣* 而有所影響）
- 轉移矩陣 (transition matrix)
可以將轉移的概率數據放到矩陣中
#### 隱藏馬可夫鏈 （ Hidden Markov Model ）
是馬可夫鏈的延伸，讓我們可以透過觀察「看得到的」現象去推測另一個「看不到的」現象
ex. 假設本來小明家沒有窗戶，所以每天都要靠出門才可以知道天氣狀態，有一天他不小心摔斷腿 沒辦法出門，所以也沒辦法知道外面的天氣如何，但是他知道隔壁鄰居在雨天的時候會有10%機率出門散布、40%機率出門購物，和50%在家打掃；在雨天的時候會有60%機率出門散布、30%機率出門購物，和10%在家打掃。
就可以因此推測今天的天氣為何。

y代表可觀查到的訊息（observe variable)，x代表隱藏的訊息（我們要藉由x去推測y 的東西）
以小明的例子來說，雖然天氣怎樣不知道，但可以透過鄰居的行蹤來推測天氣

[reference](https://pansci.asia/archives/43586)
[reference](https://pansci.asia/archives/43298)
[reference](https://qiubite31.github.io/2017/05/31/Hidden_Markov_Model_HMM/)

---

## 名字：俞辰
### Markov Models
多模態馬可夫模型是一種具有狀態的隨機過程，擴展了傳統馬可夫模型的統計模型，它允許系統在不同的狀態之間切換，而不僅僅是單一狀態，其中假設系統的未來狀態僅依賴於當前狀態，而不受先前狀態的影響。這意味著系統的過去、現在和未來狀態都是相互獨立的。而「狀態」可以是短暫的，例如生病或健康，也可能是永恆不可逆的(absorbing state)，例如死亡。

圖 1是生物統計學中使用的常見多狀態模型 (A) 是疾病-死亡模式，有時稱為殘疾模型，(B) 是進行性分期疾病模型，(C )是競爭風險模型。

多模態馬可夫模型允許系統可以處於多種可能的狀態，並且可以在這些狀態之間轉換，每個模態可能代表系統的不同行為模式或狀態。例如，假設我們正在建模一個人的日常行為，可能會有幾種不同的模態，如“工作”、“休息”和“運動”。根據不同的情況和環境，這個人可能會在這些模態之間切換。而多狀態馬可夫模型的缺點則是需要對這些狀態進行分類。

[ Reference 1](https://www.kiglobalhealth.org/resources/multistate-markov-models/)
[Reference 2](https://zhuanlan.zhihu.com/p/487589382)

### Time Series and Survival Analysis
時間序列分析是一種統計方法，專注於研究隨時間變化的數據。時間序列是一組按時間順序排列的資料點，比如：每小時的氣壓、每年的醫院急診、按分鐘計算的股票價格。時間序列資料有三個主要組成部分:趨勢、季節性、殘差或白噪聲。
時間序列資料特徵有兩個:
靜態時間序列(Static Time Series)：靜態時間序列是指資料在時間上沒有變化的情況下進行分析。在靜態時間序列中，我們通常關注資料的平均水平、趨勢和季節性等靜態特徵。常見的靜態時間序列模型包括平均數模型、指數平滑模型和ARIMA模型等。
動態時間序列(Dynamic Time Series)：動態時間序列是指資料在時間上呈現出變化的情況下進行分析。也就是說，它認為觀測到的時間序列資料是隨時間變化的，並且過去的值對未來的值有影響。在動態時間序列中，我們關注資料的動態性、趨勢變化和週期性等動態特徵。常見的動態時間序列模型包括自迴歸移動平均模型（ARMA）、自迴歸積分滑動平均模型（ARIMA）和向量自迴歸模型（VAR）等。

生存分析，研究的是隨訪中研究對象發生我們關心的事件與否，以及比較發生該事件之前時間的長短 (生存時間) 的一種分析方法。生存數據的常見例子有:死亡 (all cause);診斷/治療後直至死亡發生的時間;
孕婦的懷孕時間 (孕期長短);對象以健康狀態進入研究時開始，直至其診斷爲患有某種疾病的時間。

生存分析中的常見術語:
* 生存時間 survival time = 失敗時間 failure time = 事件時間 event time。
* 生存分析本身常被叫做事件史分析 time-to-event analysis。

生存分析的結果可以用來回答我們關心的問題有:
1. 研究特定人羣中，在某段時間內人口生存 (或死亡) 的模式 (平均壽命)
2. 比較兩組或多組人羣之間，不同的特徵導致的死亡時間的差異大小的估計
3. 研究多種變量 (例如體重，年齡，性別，吸煙，飲食等) 和事件發生時間長短之間的關系

[Reference 1](https://allaboutdataanalysis.medium.com/20%E5%80%8B%E6%99%82%E9%96%93%E5%BA%8F%E5%88%97%E5%9F%BA%E6%9C%AC%E6%A6%82%E5%BF%B5-%E5%AD%B8%E6%9C%83%E5%B9%AB%E4%BD%A0%E5%81%9A%E5%A5%BD%E9%A0%90%E6%B8%AC%E5%88%86%E6%9E%90-c297c631b374)
[Reference 2](https://wangcc.me/LSHTMlearningnote/surv-intro.html)

---
## 名字：靖涵
### Markov Chains 馬可夫鏈
- 最重要的概念是：
1. 「未來(**future state**)僅受現在(**current state**)影響，不會受其他時候的狀態影響」。
例如：明天午餐吃什麼(future state)，只會被今天午餐吃什麼影響(current state)。而不同 state 之間的轉換稱為 **transition** (form one state to another)。
2. 另外在馬可夫鏈中，從一個 state 出發的所有 arrow 加起來會為 1（因為他們代表的是機率）。(如下圖)

- 先把原本的 transition probability 以 adjacency matrix(相鄰矩陣) 表示，所以也可以稱為 **transition matrix** ，如下圖是 current state 為 pizza 的例子：[0 1 0] ，乘上 transition matrix 後得到 future state 的 probability。
**π**：可以用來標示 current state 的機率。

- **the stationary distribution/the equilibrium distribution**：即機率收斂變成固定，但若僅用多次相乘去找收斂後的固定機率可能會忽略有多個 stationary distribution 的情況，計算上較沒有效率。因此計算上可以改以 **線性代數(linear algebra)** 的方法。
所以當到達 the stationary distribution/the equilibrium distribution 時，input vector 就會和 output vector 相等。πA=π。（這個就跟之前有提到線性代數中 eigenvector equation **A x = λ x** 很相似。）

- 另外，state 在呈現某些狀態時會有不同的名稱：
- **Transient state：**
如下圖中的 state 0，只要從這個 state 出去之後就不會再回到這個 state 本身（因為沒有箭頭指向這個state）這時候就會說這個 state 是 **Reducible**。（相反，如果當每一個 state 之間都可以互相通行的話，就會叫做 **Irreducible**）
- **Recurrence state：**
如圖中的 state 1 和 state 2 只會在彼此之間相互循環變換。

[Reference_MarkovChain_1](https://www.youtube.com/watch?v=i3AkTO9HLXo&list=PLM8wYQRetTxBkdvBtz-gw8b9lcVkdXQKV)
[Reference_MarkovChain_2](https://www.youtube.com/watch?v=VNHeFp6zXKU&list=PLM8wYQRetTxBkdvBtz-gw8b9lcVkdXQKV&index=2)
### Hidden Markov Model (HMM)
- HMM = Hidden Markov Chain + Observed Variables
可分為兩大部分：隱藏狀態（Hidden States） 和 觀察序列（Observations Sequence）
**觀察序列（Observations Sequence）**:
可以直接看到的部分，但這部分其實是受看不見 **隱藏狀態（Hidden States）** 的影響，每一個 hidden state 和 observations sequence 之間都有機率分佈，而 hidden state 之間也有機率分佈。

- 以下面例子為例，其實每一天的心情好不好（Observations Sequence）是受到（並且也僅受到）今天天氣（Hidden States）的影響，而天氣之間其實就是 markov chain。從這個例子，我們無法知道今天天氣好不好，僅可以知道心情好不好。
綠色的部分為 Markov Chain 的 transition matrix，紅色是 hidden state 和 Observations Sequence 之間機率關係，可以稱為 **emission matrix**。

- 以上面的例子計算 😃 -> 😃 -> 😟 ，就可以寫成下面的計算方式，即 在已知天氣的情況下心情的 joint probability，但同時要注意到的是一開始的 晴天機率計算無法從 hidden state 中得知，所以這時候就要使用 stationary distribution 中的固定機率。

- 但我們其實無法得知 hidden state 為何，所以這時候如果只知道 😃 -> 😃 -> 😟 推算天氣的方法照理是要找出一個有 maximum probability 的 hidden state，但需窮舉計算多個 hidden state 的排列組合會很沒有效率，所以在 HMM 中是使用 **Viterbi Algorithm** 去推算最有可能的 hidden state 情況。

[Reference_HMM_1](https://www.youtube.com/watch?v=RWkHJnFj5rY&list=PLM8wYQRetTxBkdvBtz-gw8b9lcVkdXQKV&index=5)
### Viterbi Algorithm
- 在 HMM 中，從已知的 Observations Sequence 回推 hidden state，若使用窮舉法，序列計算數量會呈指數成長，會非常沒有效率。因此可以使用 **Dynamic Programming (動態規劃)** 的概念。
- **Dynamic Programming**：核心概念為「把一個大問題拆成多個小問題，然後每次計算小問題後儲存結果。」而 Viterbi Algorithm 即為一種 Dynamic Programming。
- **Viterbi Algorithm**：
即在每一個 state 都只保留機率計算出來最大的一個（如下圖公式，找出 $Ci$ X $ai,r$ , $Cj$ X $aj,r$ , $Ck$ X $ak,r$ 中最大的），其他 state 就不繼續計算，然後帶著這個 state 往下走。

如果每一步驟都如上圖所示，多個步驟就會如下圖動畫版。

[Reference_Viterbi_1](https://ckmarkoh.github.io/blog/2014/04/06/natural-language-processing-viterbi-algorithm/)

### Granger causality (格蘭傑因果關係)

- **Correlation** vs. **Regression** vs. **Causality**
- **Correlation:** 檢測 variable 之間有無關係，但沒有假設彼此之間有因果關係(**Causality**)。如果知道 variable 之間有關係，就可以進一步去檢測他們之間有沒有因果關係。檢測後如果發現他們有因果關係，就可以再進一步使用 **regression**。
- **Causality：** 在兩個 variables 之間有明確的因果關係(cause-effect relationship)。
兩個前提：
1. 變量之間需要有 correlation
2. 時間順序性（Temporal Sequence）：變量之間要有時間順序性；或者有理論基礎可以證明兩者之間是有前因後果的。
**Autocorrelation (自我相關)：** 同一時間序列中不同時間點觀測到的值之間的關聯性，範圍在 -1 至 1 之間。
**Autoregression, AR (自我迴歸)：** 統計預測模型，用於描述時間序列中當前觀察值與先前時間點的觀察值之間的關係，可以說是用過去的自己預測未來的自己。
- **Granger Causality (格蘭傑因果關係)：**
主要概念為「認為未來不會影響過去，但過去會影響未來。」
以 AR 為基礎，用一個 變數過去的值 **(lag value)** 預測這個變數自己的未來。
用來檢測一個時間序列中的一個變數 $x$ 是否影響另一個時間序列中的變數 $y$。
但也有其限制，例如少考慮其他可能的干擾因素，所以算出來是一種統計估計並不是絕對的因果關係。
[Reference_Causality_1](https://www.youtube.com/watch?v=bm6V84Lgz2w)
[Reference_Causality_2](https://blog.udn.com/gwogo/130821369)
[Reference_GrangerCausality_1](https://zh.wikipedia.org/zh-tw/%E6%A0%BC%E8%98%AD%E5%82%91%E5%9B%A0%E6%9E%9C%E9%97%9C%E4%BF%82)

---
## 名字：予茜
### Markov Models 馬可夫模型
定義：為一連串的事件串起來的模型，在不同但相關的事件當中會有其轉換的機率，也就是**狀態轉換的機率**。不同狀態間改變的機率稱為**轉移機率**(Transition Probability)。在轉換的過程中，再給定的當前狀態下，過去(即當前以前的歷史狀態)對於預測未來(即當前以後的未來狀態)是**無關**的。

要滿足兩個假設：
1.t＋１時刻系統狀態的概率分布只與t時刻的狀態有關，與t時刻以前的狀態無關。
2.從t時刻到t＋１時刻的狀態轉移與t的值無關。

例如：
下圖中為兩事件Ａ和Ｅ的馬可夫鏈。
若當前的事件為E，30%機率會轉移到相同事件E，70%機率會轉移到不同事件A；若當前的事件為A， 60%會轉移到同一事件Ａ，40%會轉移到不同事件Ｅ。

事件和事件的轉移機率可以寫成以下形式，也就是事件E轉移到A，或A轉移到E的機率。

依照上面的例子，還可以將機率寫成一個轉移矩陣：

| | 事件A | 事件E |
| -------- | -------- | -------- |
| 事件A | 0.6 | 0.4 |
| 事件E | 0.7 | 0.3 |

[reference](https://medium.com/@a5560648/hmm簡介-1acfe20e6c80)
### Hidden Markov Model 隱藏馬可夫模型
定義：為馬可夫鏈的延伸，利用觀測值來推斷狀態的一個算法。狀態被稱為**隱藏狀態**(hidden state)是因為看不到狀態，只能看到觀測值。

例如：天氣與天氣（Ｘ變數）之間可能有馬可夫鍊的關聯，而小明的心情（Ｙ變數）會根據天氣的不同而轉變。HMM就是觀察的到小明的心情，從中去推估目前的天氣。就是可以由𝑌預測出𝑋的目標函數。

X為隱藏的狀態，而Y為可見狀態。
X0到X1到X2，為一個隱含狀態到下一個隱含狀態的過程。
X0到Y0，X1到Y1，X2到Y2，為隱含狀態到可見狀態的轉換。


應用：生物資訊的DNA辨識、語音辨識處理

[reference](https://medium.com/@a5560648/hmm簡介-1acfe20e6c80)

### Granger causality 格蘭傑因果關係
是一種假說檢定的統計方法，檢定一組時間序列𝑥是否為另一組時間序列𝑦的原因。其基礎是迴歸分析當中的**自我迴歸模型**。自我回規模型可以得出變量前後期的相關性。

核心概念：**過去值**（lag value，或稱落後值）為同一變項比當期時間上更早的值。例如：當期為𝑦10，它的落後期為𝑦𝑖<10

假設：**未來的事件不會對目前與過去產生因果影響**，而過去的事件才可能對現在及未來產生影響。也就是說，如果我們試圖探討變數𝑥是否對變數𝑦有因果影響，那麼只需估計𝑥的落後期是否會影響𝑦的現在值。因𝑥的未來值不可能影響𝑦的現在值。**假如控制了𝑦變數的過去值以後**，**𝑥 變數的過去值仍能對Y 變數有顯著的解釋能力**，就可以稱𝑥能「Granger 影響」𝑦。

侷限：Granger 最初提出時，並未納入干擾變數的分析，而是假設其他可能解釋變數的資訊包含在𝑦的落後值中。事實上帶來因果關係的是**第三變數**（干擾變數），亦即若事實上操控 𝑥並無法改變𝑦，格蘭傑因果關係的虛無假說仍然可能被拒絕。因此格蘭傑因果測試可能會產生誤導性。

[reference](https://zh.wikipedia.org/zh-tw/格蘭傑因果關係)

---
## 名字：植棻

### Growth curve analysis

Growth curve analysis 是一種多層次迴歸技術，旨在分析時間序列 (time course) 或縱向數據 (longitudinal data)。這種方法的一個主要優勢是可以同時分析 group-level effects（例：實驗操作）和 individual-level effects（例：個體差異）

Growth curve (生長曲線)有許多不同的形狀呈現，以下舉三個例子：

**S-shaped curve**
S型曲線是常見的生長曲線，分為三個階段，第一個階段是緩慢的成長，第二個階段快速的成長至一定的高度後，進入第三階段回歸穩定，趨於飽和。這種型態通常是呈現生物體的生長或是經濟學中市場的擴張。

**U-shaped curve**
曲線從一開始在一段時間內往下降，在出現低谷之後往上回升。這種型態通常是一個市場或是系統進行變動會產生的狀況。

**J-shaped curve**
曲線一開始在短期內急速下降至谷底後又反彈上升。這種型態通常是與新市場、新技術發展相關，一開始發展不順，但隨即會有快速的成長。

[Ref](https://www.danmirman.org/gca)

### Survival analysis

Survival analysis可被稱為**存活分析**或是**生存分析**，是指在某特定時間起，經過一段時間(time)的觀察追蹤，直到特定事件(event)的發生，所以也可稱為**time-to-event**的分析。

**名詞定義：**
- 起始點(starting event time point, zero time point)：確診時間或是手術的時間點。
- 觀察追蹤(follow-up)：在起始時間到特定事件的發生之間這段時間的紀錄。
- 特定事件的發生(endpoint, event)：死亡或是疾病復發。
- 設限(censoring)：發生追蹤到一半，個案就失聯或被剔除(原因可能是競爭死因或是不良藥物反應)

**生存分析試圖回答：**
- 能夠存活超過一定時間的人口比例是多少？
- 在那些倖存下來的人中，他們死亡或失敗的機率是多少？
- 是否可以考慮死亡或失敗的多種原因？
- 特定環境或特徵如何增加或減少生存機率？

**生存函數(survival function)：**

==$S(t)=Pr(T>t)$==

- $t$ 表示某個時間
- $T$ 表示生存的時間（壽命），
- $Pr$ 表示表示機率

生存函數就是壽命$T$大於$t$的機率，是一個遞減的函數(decreasing function)。舉例來說：人群中壽命超過50($t$)歲的人在所有人中的機率是多少，就是生存函數要描述的。

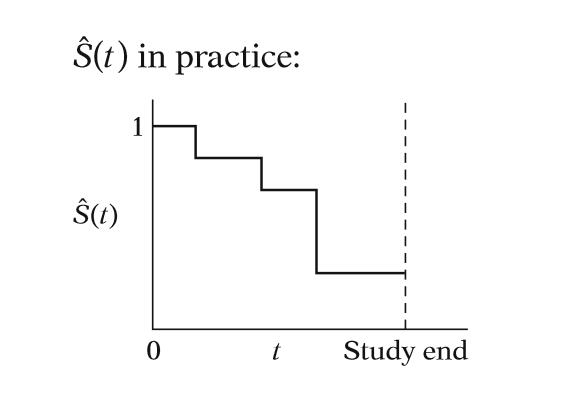
在實際情況可以看到每個時間點如果像階梯往下的部分，代表的是有個案的死亡，下降的幅度越大代表死亡個數越多。

### 生存分析的不同算法

- 無母數的統計有 Life-table method跟Kaplan-Meier method
- 有母數的統計則是 Cox proportional hazards model

**Life-table method & Kaplan-Meier method**

兩者的差異是Life-table method的製作是依照**固定區間**，Kaplan-Meier method則是依照個案的**存活時間點**。
舉例來說：生命表如果以月為單位，則資料內在同一月份發生事件者會在同一格。一般而言，研究的個案數大於30例，則考慮使用生命表法來計算存活率較方便，反之，則使用KM法。

**Cox proportional hazards model (Cox比例風險模式)**

當存活資料中另有共變數(covariates)或風險因子(risk factors) 時，Cox model可用來推估這些共變數對存活時間的影響，也可用來預測特定時間的存活機會。

**風險函數(hazard function)：**
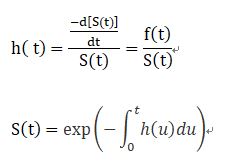
風險函數$h(t)$值為定值，因為針對某一危險因子，其風險比不可隨時間而改變。$t$是時間點，風險函數$h(t)$值與存活時間有關。
舉例來說，如果$t$=3個月，$h(t)$就是事件機率（死亡）除以3個月時的生存函數。因為$t$越大，存活函數$S(t)$越小。假定死亡機率密度$f(t)$對任何時間點一樣，那麼風險函數$h(t)$值越大，預期存活時間短。

[Ref: Life-table method](https://www.yongxi-stat.com/survival-analysis/)
[Ref: KM method](https://www.yongxi-stat.com/kmmethod/)
[Ref: Cox model_1](https://www.yongxi-stat.com/cox-regression/)
[Ref: Cox model_2](http://rweb.tmu.edu.tw/stat/step1.php?method=coxreg)

---
## 名字：喻璞
### Simulation study 模擬研究
模擬是出於多種原因（包括教育、為預期事件做準備或解決問題）而創建現實世界場景模型的過程。模擬過程中使用的模型可能是真實的或戲劇性的。

### Granger causality (GC) 格蘭傑因果關係
格蘭傑因果性是一種基於預測的統計因果性概念。(近幾年流行於神經科學中的應用)

一個時間數列是否有辦法預測另外一個時間數列的行為
> 如：每天跑步的時間是否有辦法預測自己的預期壽命?

如果想預測「壽命=Y」時間數列的行為，而我們活在一個含有「跑步時間=X」之資料的宇宙中，我們有拿「X」去預測「Y」：
1. 發現相較於我們拿掉「X」之資料後去預測竟然沒有比較好，則表示「X」沒有「Granger影響 (Granger Cause)」「Y」。==數學語言上,X ~GC Y)==
2. 如果加入X以後會有比較好的預測效果, ==則X GC Y==

也就是說 GC 評估了一個時間序列基於另一個或多個其他時間序列的可預測性，如果一個時間序列包含的信息能夠更好地預測另一個時間序列的未來，那麼就暗示著因果關係。

GC 檢定假設了有關 y 和 x 每一變數的預測的資訊全部包含在這些變數的時間序列之中。且進行格蘭傑因果關係檢定的一個前提條件是時間序列必須具有**平穩性**，否則可能會出現虛假迴歸問題。

#### 檢測方法
通常情況下，GC涉及線性自迴歸建模，但也可以包括非線性、時變和非參數模型。
- 通常是用自我迴歸(Autoregression)來做。
- 如果想要同時對多個變數的自我迴歸分析則會使用向量自我迴歸(Vector Autoregression, VAR)。

p.s. 格蘭傑因果關係從嚴格的數學定義上，並不能叫做因果關係

#### Transfer entropy (TE) 傳輸熵
是GC的理論擴展。在神經科學研究中，TE 可以區分由共同歷史導致的信息並確定神經迴路中的反饋。它考慮了線性和非線性流，並且可以量化脈衝序列之間的因果強度。

與標準的 GC 相比，信息理論測量的一個優點是它們對非線性信號特性敏感，但轉移熵的一個限制是它目前僅限於雙變量情況。不過信息理論測量 (TE) 通常需要比回歸方法 (GC) 更多的數據。

[ref1](https://www.facebook.com/MathKingdomFaraway/photos/a.1419361811717573/2022737801379968/?type=3) [ref2](https://www.sciencedirect.com/topics/neuroscience/granger-causality) [ref3](http://www.scholarpedia.org/article/Granger_causality)

### Survival Analysis 存活分析

存活分析，也稱為事件時間分析，研究特定感興趣事件發生之前所需的時間。從一時間點至事件(event)發生的時間(time to event)，稱為survival time。

- start time: 研究起始時間（確診癌症時間）
- end time: 研究結束時間（死亡時間）
- survival time= 事件發生時間 – 追蹤的起始時間 (must > 0)

如，人壽保險公司的分析師使用存活分析來概述在特定健康狀況下不同年齡的死亡發生率，計算適當的保險費。

#### 統計方法 （無母數分析）
大部分的存活分析的資料通常**不是**常態分佈。
- Kaplan-Meier
- 常用來估計存活曲線的方法
- 可估計存活中位數及不同時間點的存活率
- 僅能了解不同組別的存活曲線分佈
- Log-rank test
- 比較組別間是否差異
- Cox Proportional Hazards Model
- 評估多個變數對存活(Time to event)的影響
- 可使用類別/續變數呈現危險因子，並估算出這些危險因子對outcome的影響

#### 優點
- 將「時間」變項列入分析的統計方法。

#### 缺點
- 線性迴歸通常同時使用正數和負數，而存活分析處理的是嚴格正數的時間。

[ref1](https://www.investopedia.com/terms/s/survival-analysis.asp) [ref2](https://www.vghtc.gov.tw/UploadFiles/WebFiles/WebPagesFiles/Files/698439da-e1f5-43f9-9b16-6cd86cadcd4e/20221214-%E8%AA%B2%E7%A8%8B%E8%AC%9B%E7%BE%A9.pdf)

### illness-death model 疾病-死亡模型
- 當你有**多個**感興趣的事件時可以使用。
- illness-death model 由三種狀態組成：未患病 nondiseased、患病 diseased 和 死亡 dead。
- 可計算不同區間的人口群體和狀態之間的轉移機率。

#### 在醫療上的應用：
- 可估計在不同時間點上處於每個狀態的概率，如：涉及盛行率、發病率、死亡率和緩解。
- 估計轉移風險，即風險/預防因素對疾病和死亡的影響。
- 如：在非傳染性疾病模型中，我們感興趣的是群體中個體從健康或易感狀態到患病狀態，然後從患病狀態或直接從易感狀態死亡的轉變

[ref1](https://med.mahidol.ac.th/ceb/sites/default/files/public/pdf/CMU/2016/Survival%20analysis%20part%20III%20Illness-death%20model%2024-09-2016.pdf) [ref2](https://www.hindawi.com/journals/cmmm/2018/5091096/) [ref3](https://www.frontiersin.org/articles/10.3389/fepid.2022.903652/full)

### Multistate Markov Models

多階段馬可夫模型由狀態和狀態之間的轉換來定義。

狀態可以是短暫的，個體可以不同狀態進入和退出。狀態也可以是吸引人的，個體一旦進入就永遠不會退出（例如死亡）。

最簡單的模型包含兩種狀態，例如 alive/dead 或 healthy/ill，通常稱為死亡率模型。p.s. 可以使用存活分析 (survival analysis) 來分析此類模型。

多階段馬可夫模型可用於估計過渡風險（從一種狀態過渡到另一種狀態的瞬時風險），以及在給定狀態下的過渡機率和平均停留時間。

#### 優點
- 能分析個體經歷一種(以上)的事件的縱向資料。
- 可以允許在兩個方向上的狀態之間移動。
- 馬可夫模型由於其簡單性而被最常使用。

#### 缺點
- 需要對狀態進行分類，將連續變數分為離散類別。

[ref](https://www.kiglobalhealth.org/resources/multistate-markov-models/)

---
## 名字：孟桁

### Survival Analysis
Tells the expected duration until an event occurs (i.e. how much time an organism is expected to have until its death). Commonly used in describing survival times of members, comparison of survival times in multiple groups or exploring the effects a variable may have on survival rates. Kaplan-Meier plot is a common method in survival analysis to describe survival time.

Key terms:
Event: target states to be observed
Censoring: occurs when a member is documented, yet the exact survival time is unclear.
Survival function: probability that a subject survives past the time.

Cox Proportional Hazard model
A type of model in survival analysis for exploring a variable’s relationship to survival rates.

---

<!-- ## tags, 拜託不要刪除以下 -->
###### tags: `QL2024`

<!-- ---

## 名字：
### 以下如果要用到標題請打三個以上的井字號 -->