:dart: W5 - Entropy
===

<!-- ## Table of Content
[Toc] -->

## 名字：瓈萱
### Moving average type-token ratio
改良版的type-token ratio
算法：設一個windo-size (ex. 50字)，每一個window-size 都去算他的type-token raitial 然後一直到做到結束 ex. 1~50 2~51 3~52...以此類推。之後把所有值加起來做平均。
優點：
1. 不會受到文本長度的影響
2. 除了可以對比文本間的不同，可以藉由把每一次windowsize 計算出來的TTR的點都標出來，可以看到詞彙豐富度在文本內的變化。

### entropy (熵）
最早概念起源是在物理學，後來再資訊理論中變成一個很重要的概念（被shonnon 等人引用，所以之後為了要區分，都會叫shannon entropy)是用來計算資訊量的混亂程度(不確定性多高），越混亂代表所帶的訊息量越多。

* 公式：
其中p(x)代表 x 出現的機率，而關鍵是後面的logp(x)，如果前面的機率越低，取log 加成之後的值反而會比較高（也可以說是這個資訊的驚喜程度）
ex. 有一個袋子總共有100個足球巧克力跟兩個GODIVA的巧克力，如果你抽到GODIVA 巧克力大家都會很驚訝（類似這個概念)，如果這種驚訝情況越多就表示整體的不確定性越高。

換作是用來看文本的詞彙豐富程度來說，如果某個字很少在這個文本出現 他的entropy值也會越高，因此整個文本的entropy很高的話，就也可以代表這個文章的詞彙豐富（複雜）的是高的。
相較於type-token ratio的方法，只看type 跟token，這個方式也考量了整體分佈的情況。

* 其他應用：
可以觀測一組數據資料變動的情況，如果有數據的熵值突然變很大或很小 可能就代表有地方出問題。
也可以用來觀測descion tree 的分類結果越混亂越不明確，熵值會越大，代表分類的效果不太好，可以更換特徵或移除。

---

## 名字：俞辰
### Ergodicity (遍歷性)
遍歷性是指一個隨機的過程中，統計結果在時間上的平均數與空間上的平均數相等。如果一個系統具有遍歷性，在兩個情境之下的結果應該是相同的。就像如果你重覆拋一個硬幣，正面與反面的機率各為50/50，和我也重複拋一個硬幣，正面與反面的機率也是各為50/50，這就表示拋硬幣這個隨機過程是具有遍歷性。

[Reference](https://jcinsight.info/ergodicity/)

### Entropy (熵)
Claude Shannon 於 Information Theory 研究中提出熵(entropy)的概念，可以說是影響後續機器學習(machine learning)發展相當重要的概念。用以衡量一組資料的不確定性(uncertainty)。

假設有 1 枚硬幣 2 面都是人頭，那麼不管如何投擲，我們都能夠確定它的結果是人頭，因此毫無不確定性可言，那麼熵值就會是 0 。
假設有 1 枚硬幣 正面人頭，背面為字，那麼我們有 50% 的機率猜中其投擲結果，因此該情況下具有不確定性，其熵值為 1 。
假設有 2 枚硬幣，那麼我們約有 33% 的機率猜中其投擲結果（正正、反反、正反），該情況的不確定性相對於只有 1 枚硬幣而言更高，其熵值約為 1.58 。

可以看到隨著不確定性增加，熵值也會增加。不確定性也可能會造成混亂的局面，不確定性越高代表越難預測結果，因此結果越混亂，所以我們也能夠透過熵值衡量資料分散、混亂的情況。

熵的公式:

P(x) 代表 x 出現的機率，例如 1 組數據 [1, 2, 2, 3, 3, 4] ，其中數字 1, 4 只出現 1 次，其機率皆為 1/6 , 而數字 2, 3 都出現 2 次，其機率皆為 2/6 。

因此前述數據組的熵值為：
-(1/6 * log2(1/6)) -(2/6 * log2(2/6)) -(2/6 * log2(2/6)) -(1/6 * log2(1/6))
= 1.9182958340544896

而 Entropy 的關鍵部分在於 P(x) * log(P(x)) 的數學意義：某資料出現的機率越低，在 log 的加成下該數值會提高，整體的不確定性/混亂程度就會提高。

[Reference](https://myapollo.com.tw/blog/shannon-entropy-explanation/)

### Moving-Average Type–Token Ratio
Moving-Average Type–Token Ratio是用一個預設的移動視窗去計算樣本的詞彙多樣性，而這個移動視窗為每個固定長度的連續視窗之TTR估計值。假設在10個單字中，先計算1-10的TTR，再計算2-10的TTR，接著是3-10的TTR，以此類推。最後，計算所有TTR的平均。透過移動視窗的預設長度計算TTR，此方法可以避免文章長度對於計算詞彙多樣性帶來的影響。

[Reference](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4490052/)

---
## 名字：靖涵
### Entropy (Information Entropy)
- Entropy (熵) 的概念出自於熱力學，描述物理系統之無秩序或亂度的量度。之後在資訊領域也有 information entropy 「資訊熵」的概念，描述資訊的「不確定度」。

- 在理解上可以從「事件發生所帶來驚奇程度的平均值」幫助理解，因此講 entropy 之前需要先講 驚喜度(surprise)。
舉例：今天箱子裡面有 999 顆橘色球和 1 顆藍色球，伸手抽出橘色球的 機率(probability) 就遠高於抽出藍色球的機率。如果今天只抽一次就抽出藍色球，相對的驚喜度就會很高。

所以可以說，越低的機率會有越高的驚喜度；相反來說，越高的機率，驚喜度就會相對比較低。

聽起來機率和驚喜度是相反的，但兩者之間的計算不能單純以倒數呈現，其中原因之一如果機率 = 1，機率倒數 (inverse of probability) 之後驚喜度會 = 1。
例如：有一個硬幣怎麼躑都是正面，這樣正面的機率為1。在倒數之後，驚喜度還是為1。如果想要這時候的驚喜度為 0 的話，就**必須取log** (log1=0)。另外，如果硬幣只會出現正面，這樣出現反面的機率為 0，而分母不可為0，同時可以解釋為量化不可能出現事件的驚喜度是沒有意義的。（如下圖）

- Note: 當像在硬幣這樣的例子中，只會有正面或反面的兩種情況時，通常在計算這樣例子的驚喜度取log時會使用底數2，而非底數10。

- 如下例子，在計算硬幣 正面(p=0.9) 和 反面(p=0.1) 的時候，可以看見例子中「兩次正面後一次反面」的機率為 (0.9 * 0.9 * 0.1)。下圖計算其驚喜度 ( 即log₂(1/probability) )的結果最終其實就等於**驚喜度的加總** (probability: 0.9 = surprise: 0.15 ; probability: 0.1 = surprise: 3.32)。


- 假設現在躑硬幣100次，計算平均的驚喜程度，也就是正面出現100次跟每次帶來的驚喜程度，還有反面出現100次以及其帶來的驚喜程度，最後除以100，就可以計算出每一次躑硬幣的平均驚喜程度，也就是 Entropy（每一次躑硬幣的不確定度）。

- 從上面可以看到分子和分母的100（躑硬幣100次）可以對消，所以其實 entropy計算上就是每一個機率和其驚喜度相乘之後的總和（如下圖）。

- 從這裡就可以進一步去推導出 Entropy 的公式：
把 `log(1/p(x))` 拆解成 `[log(1) - log (p(x))]` ，因為`log(1) = 0` 所以這部分又可以等於 `[0 - log(p(x))]` ，即 `- log (p(x))`，把負號往前移就可以得到 Shannon 最初提出的 Entropy 公式如下：

$$ H(X) = -∑ p(x) * log(p(x)) $$

- 而 Entropy 可以用來量化相似和相異程度，也是 Decision tree 中決定樹要如何往下做每一個決策的衡量標準之一。

[Reference_Entropy_1](https://www.youtube.com/watch?v=YtebGVx-Fxw)
[Reference_Entropy_2](https://medium.com/%E4%BA%BA%E5%B7%A5%E6%99%BA%E6%85%A7-%E5%80%92%E5%BA%95%E6%9C%89%E5%A4%9A%E6%99%BA%E6%85%A7/entropy-%E7%86%B5-%E6%98%AF%E7%94%9A%E9%BA%BC-%E5%9C%A8%E8%B3%87%E8%A8%8A%E9%A0%98%E5%9F%9F%E7%9A%84%E7%94%A8%E9%80%94%E6%98%AF-1551e55110fa)

### Relative entropy vs. Cross entropy

- **Relative entropy**
又稱為Kullback-Leibler distance、Kullback-Leibler divergence（KL散度）。
$$ D(P || Q) = ∑ P(x) * log(P(x)/Q(x)) = ∑ P(x)logP(x) - P(x)logQ(x) $$

- 是用來量化兩個機率（P 和 Q）分佈的相對差異有多大，計算兩者之間的差距。從上面公式也可以解釋為「需要**額外**多少個資源，才能用 機率分佈P 完整描述 機率分佈Q」。
因此當兩者分佈相同時，relative entropy 會為0；而兩者分佈差異越大的話，relative entropy 越大。

- **Cross entropy**
用來衡量一個機率分佈 Q 對於一個機率分佈 P 的表現的指標。
從公式來看，cross entropy 只考慮 relative entropy 的後半，即「若用表示 機率分佈P 的方式描述 機率分佈Q 需要多少資源」。
$$ H(P, Q) = -∑P(x) * log(Q(x))$$

- 機器學習中理想會希望模型預測答案跟正確答案之間越相近越好，為了計算模型預測出的標籤分佈和正確答案的標籤分佈之間的差異，cross entropy 可以用來當作模型訓練的 損失函數(loss function)。P 即為真實數據的機率分佈，而 Q 為模型預測的機率分佈。因此，計算出來的 cross entropy數值越小，即預測出來的結果跟真實數據越相近。

[Reference_relative/cross_entropy_1](https://flag-editors.medium.com/%E6%A9%9F%E5%99%A8%E5%AD%B8%E7%BF%92%E5%8B%95%E6%89%8B%E5%81%9Alesson-10-%E5%88%B0%E5%BA%95cross-entropy-loss-logistic-loss-log-loss%E6%98%AF%E4%B8%8D%E6%98%AF%E5%90%8C%E6%A8%A3%E7%9A%84%E6%9D%B1%E8%A5%BF-%E4%B8%8A%E7%AF%87-2ebb74d281d)

---
## 名字：植棻
### Moving Average Type-Token Ratio (MATTR)

**Moving average 移動平均**

主要是將一大筆資料，分成小小的組別去取其平均，然後這些小小的組別會移動，每算完一組，會將**舊資料中的頭一筆剔除**，並且再**加進一筆新資料**，形成新的小小組，接著再計算新的平均數。如此一來小組資料的數量是不會變動的，不過數量大小可以在計算時自訂。

最常見的例子是用股市收盤的趨勢圖。假設有一月份每日收盤價的資料，想要了解趨勢，可以自訂要用幾天為一組來取平均數（e.g., 5, 10）

如果是用5天為一組，則**第一次會計算1/1—1/5**的收盤價平均，**第二次會計算1/2—1/6**，以此類推。這樣的方法可以畫出移動平均線。


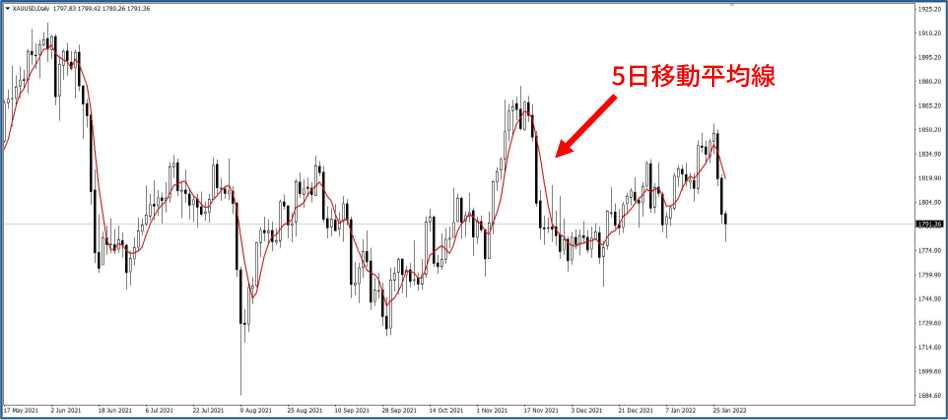
[Reference _1](https://wiki.mbalib.com/zh-tw/%E7%A7%BB%E5%8A%A8%E5%B9%B3%E5%9D%87%E6%B3%95)
[Reference_2](https://fxlittw.com/what-is-moving-average/)

**Type-Token Ratio (TTR)**

用來計算詞彙多樣性。下面的句子為例 “The old man loves the young man.”
token =7, type =6（兩個man算同一個type）
$$ TTR=types/tokens$$

[Reference](https://www.tcrc.edu.tw/TANET2013/paper/H13-966-1.pdf)

**Moving Average Type-Token Ratio (MATTR)**

這個方法是在計算TTR的時候會移動window size，每一個window size算出TTR，最後再加總取平均。

[Reference](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4490052/)

### Change point detection 變點檢測

是指一筆資料序列，在某一個時間點上受到影響產生變化，該時間點稱為變點。（雖然講解都用time但不一定只會是時間）

以**使用時機**可以分為兩種：

- Online: 觀察某一現象的過程，如遇到變點則停止檢測。主要著重在現在的數據，用於**事件預警**。
- Offline: 從過去已經發生的資料中找尋變點，用於**歷史檢驗**。

以**變點類型**主要可以分為四種：

- 平均數變點


- 標準差變點


- 線性趨勢變點


- 個數變點


[Reference_1](https://pro.arcgis.com/en/pro-app/3.1/tool-reference/space-time-pattern-mining/how-change-point-detection-works.htm)
[Reference_2](https://blog.csdn.net/u013468614/article/details/82589020)

---
## 名字：喻璞

### Entropy

#### 基本定義
我們可以用 **probability of the event (事件的機率)** 來計算事件中包含的資訊量。

> $information(x) = -log( p(x) )$

- 低機率事件：高資訊（令人驚訝）。
- 高機率事件：低資訊（平平凡凡）。

probability distributions 機率分佈:
- Skewed Probability Distribution (偏斜機率分佈-平平凡凡): Low entropy
- Balanced Probability Distribution (平衡機率分佈-令人驚訝): High entropy


[ref](https://machinelearningmastery.com/what-is-information-entropy/)

#### lexical richness
- 近期常用 entropy 衡量詞彙豐富度
- 優點：
- 考慮了文本中單詞的frequnecy infomation：**多樣性**以及它們在文本中**分佈**的均勻性
- 爭議：
- entropy-based methods of lexical richness 是否對文本長度敏感？眾說紛紜

#### The Naïve Estimation of the Shannon Entropy
$H_{s}=-\sum_{i=1}^{n}P_{i}log_{2}P_{i}$
- 文本的Entropy越大
= 表示文本包含的獨特單詞越多
= 這些單詞在文本中的分佈越均勻
= 文本的不確定性越高
= 詞彙豐富度也越高

#### The Zhang Estimation of the Shannon Entropy
$H_{z}=\sum_{i=1}^{V}P_{i}\sum_{v=1}^{T-f_{i}}\frac{1}{v}\prod_{i=0}^{v-1}\left ( 1+\frac{1-f_{i}}{T-1-j} \right )$

因為Naïve Estimation的缺點 -- 不準確的估計值 (lack of ergodicity in a limited corpus data)，因此有了Zhang Estimation與其他算法。

> ergodicity 遍歷性
>> 時間平均值與空間平均值相類似。

> Yakov Sinai:
假設你想買雙鞋且你家樓下就是間鞋店。你有兩個辦法: 一個是你每天到樓下去找鞋子，最終你會找到最棒的一雙鞋。另一個則是你開車到鎮上花一整天四處找鞋，找有賣有最棒一雙鞋的地方。若這兩個辦法得出的結果一致，則該系統具遍歷性。 [ref](https://medium.com/@jackhsujack/%E9%81%8D%E6%AD%B7%E6%80%A7-ergodicity-83353ab0e7f2)

### Type-Token Ratio (TTR)
$\ type-token\ ratio= (number\ of\ types\ number\ of\ tokens) * 100$

傳統上經常測量 lexical richness / variation 的方式。
- 不同詞彙 types
- 詞彙總數 tokens
- 該測量值介於 0 和 1 之間
- 如果文本中沒有重複，則該測量值為1；高 TTR 表示大量詞彙變化大
- 如果有無限重複，則該測量值將趨於0；低 TTR 表示詞彙變化相對較小 [ref](https://medium.com/@rajeswaridepala/empirical-laws-ttr-cc9f826d304d)

> 口語 vs 書面
>> 口語因為是即時產生，一個人思考和計劃想說的話的時間是有限的，因此說話者傾向於從相對有限的詞彙中選擇單字，所以通常 TTR 較小。書面文本的作者因為有更多的時間來規劃和選擇詞彙，因此通常TTR較高，詞彙豐富度較大。
[ref](https://www.sltinfo.com/type-token-ratio/)

缺點：
- 容易受到 text lentgh (文本長度) 影響。(McCarthy & Jarvis, 2007; Richards, 1987)
- 所以如果 text lentgh 大的話，新詞的出現機率就會拉低，導致長文本的 lexical richness 低。
- 如果兩本文長度不同時，就不適合用此方法比較。

試圖解決 TTR 受文本影響的問題而提出的算法：
- Guiraud’s Index (1954)
- Herdan’s Index (1960)
- Somers’ S (1966)
- D (Malvern & Richards, 1997; McCarthy & Jarvis, 2007; Mckee et al., 2000)
- K (Yule, 1944)
- Moving Average Type-Token Ratio（MATTR）
- 它可以捕捉文本內部和文本之間的差異
- 消除了文本長度的影響因此已被廣泛使用於文本比較
- 算法："Choose a ==window length== (say 500words) and then compute the TTR for words 1–500, then for words 2–501, then 3–502, and so on to the end of the text. The ==mean== of all these TTRs is a measure of the lexical diversity of the entire text and is notaffected by text length nor by any statistical assumptions." [ref](https://www.tandfonline.com/doi/full/10.1080/09296171003643098?casa_token=_hzU9teXgzsAAAAA%3AOZL_WbGhQnALwF7vfbheetJnRbtxf8j7kz2-wO0WELX0b8FzJXP7JXlTugL7VWGdv9Bmr_0q8mE3VQ)

### arc length (L)
- 數學定義：arc length 弧長，也就是曲線的長度
- 詞彙豐富度的算法(I.-I. Popescu et al., 2008)：利用單字的排名頻率分佈(rank-frequency distribution)的弧長計算 [ref](https://www.ram-verlag.eu/wp-content/uploads/2018/08/g17zeit.pdf)
- 算法：兩個相鄰頻率之間的歐幾里德距離總和
- 缺點：會受到文本長度影響，雖然後來有人提出relativized L - lambda (Λ)，但仍然沒有解決問題

---

<!-- ## tags, 拜託不要刪除以下 -->
###### tags: `QL2024`
## 名字：予茜
### Entropy(熵)
最早是物理學家Shannon在1948年所提出的觀念，是用來指物理的的混亂程度，最早用於熱力學中。現今放在訊息理論來說，代表一個訊息所帶有的資訊量，或者說無法預測的程度。

以語言學來說，可以計算文本中的詞彙豐富程度，也就是在文本中的字詞不可預測性。當一個文本中的word type越多，代表它的亂度越大，越難預測下一個字是什麼，表示其entropy越大，詞彙豐富度越高。

公式:

P(x)代表x所出現的機率，-logp(x)代表x所帶有的資訊量。
熵是隨機變數的不確定性的平均度量數，隨機變數變異數越大，即隨機變數越「亂」，則熵之值越大。

舉例:

1.在文本中可能有N個word type，如果每種的情況出現的機率相等，那麼N越大，熵就越大。

2.若資訊可能有N種情況時，當N一定，那麼其中****所有情況的機率******相等**時，熵是最大的。而如果有一種情況的機率比其他情況的機率都大很多(一邊倒的情況or某個詞的頻率很高)，那麼資訊熵就會越小。

[reference](https://medium.com/人工智慧-倒底有多智慧/entropy-熵-是甚麼-在資訊領域的用途是-1551e55110fa)
[reference](https://ithelp.ithome.com.tw/articles/10305380)
### Change point detection (變點偵測)
change point(變點)，最早是由Page(1955,1957)提出。指的是在某一位置或時刻，在這個點的前後觀測值或數據，是遵循兩個不同的模型。

變點偵測旨在觀察時間序列資料中平均值、變異數或分佈的變化。可以用來觀測(1)**水平移動**(2)**趨勢變化**，「水平移動」是指當時間序列值的平均值顯著變化；而「趨勢變化」是當趨勢的方向或斜率顯著改變時，如下圖：

紅色的圈標示水平移動，而綠色的圈則標示趨勢變化。
若套用在商場上的分析，可以看做是某產品有了新的銷售通路（例如線上購物平台）或法律環境發生變化（例如，藥品獲得補貼）時，可能會發生**水平轉變**。這種變化通常會導致平均值更高。實際銷售額的平均值也有可能下降；例如，當新的競爭對手進入市場或補貼終止時。

而趨勢變化發生在兩種情境，第一種：兩個相鄰斜率變化**大於**預測的最小百分比，例如因為聖誕節臨近，某種產品的銷售在11 月出現積極趨勢，並且在12 月該趨勢繼續以更陡峭的斜率，則演算法將識別時間序列中的趨勢變化；第二種：兩個相鄰的斜率變化不足以滿足最低要求，但也可以在部分之間觀察到**顯著的水平移動**，例如11 月某種產品的銷售呈現*正面趨勢*，且該趨勢在 12 月*以相同的斜率持續，但數值較高*，則即使趨勢的斜率沒有變化，演算法也會識別出趨勢變化。

[reference](https://help.sap.com/docs/SAP_INTEGRATED_BUSINESS_PLANNING/feae3cea3cc549aaa9d9de7d363a83e6/be9bc5e98fc244269e18aab55432f386.html)

### arc lenth(L)
The sum of Euclidean distances between two neighbouring frequencies.也常用來比較不同的作者、類型或是語言。但是和TTR(token-type ratio)一樣，都仰賴text length。但是entropy不一樣，可以計算到不同詞彙的頻率和「分布」。

---
## 名字：孟桁
**(Shannon) Entropy**
Shannon entropy is the first adaptation of the notion of entropy in physics to information theory. The log formula here is a numeric representation of probability and surprise.

Supposedly an event has a high chance occurring, the less likely you would be fazed by its occurrence when it did happen. A high probability indicates a regular occurrence, and further indicates low relevance of this event compared to that with a rare occurrence.

In computation, this numeric value of relevance is represented as “bits”. The higher the relevance, the larger the bits, which translates to more information encoded in said event. These bits are the minimal required to encode said info, and it is allowed for one to use more bits in encoding, thus entropy is also defined as “the minimal number of bits necessary to encode information in binary form”.

The problem with this formula however, is that the estimation assumes the probability of a word non-existent in the given text to be zero. Realistically, word frequency depends on context (i.e. genre, author) and with this assumption the result cannot be replicated easily with other text samples, hence the lack of ergodicity.

**Cross Entropy & Relative Entropy**
Cross entropy and relative entropy (Kullback-Leibler divergence) both evaluates a model’s performance by comparing the true distribution (exact sample points unknown, represented with Shannon entropy because it is the lower bound for the encoded samples as a whole) with an approximated distribution. The goal with cross entropy is to make the approximated distribution as similar to the true distribution as possible.

KL divergence compares the distributions a sample-point level, and the formula can be written as the value of cross entropy minus the value of Shannon entropy.

**Exponentially Decay**
The opposite of an exponential growth, which means the decreasing rate slows down in proportion to the quantity left.

<!-- ---