:dart: W9 - Chi-square & Dependency Distance
===

<!-- ## Table of Content
[Toc] -->

## 名字：瓈萱
### Kruskal-Wallis檢定
- 簡稱K-W檢定

ANOVA 可以用來檢定多個母體之間的平均是否相等，但當如果資料不符合常態分佈，變異數不相同，且要用來檢測三組以上的獨立樣本母體之間的差異就可選用無母數方法中的Kruskal-Wallis tset (又稱H檢定法) 檢定來取代，這個用法不需要常態分佈假設就可以使用。

H0假設：各組的中位數均相等
H1假設：至少有兩組中位數不相等
算式：

（樣本數要>5)
R=個組排名的總和,n=總共有幾筆資料

計算步驟：
1. 將所有觀察值進行排序（所有資料一起排序）
2. 計算個組之間排序的和
3. 套入公式進行計算，算出來的值之後搭配自由度去查表，如果高於臨界值則否定H0假設

補充：
1. 有母數檢定 vs 無母數檢定
parametric method vs. nonparametric method：

- 有母數分析方法(檢定)：
假設==母群體為常態分布==以進行檢定的方式
代表檢定：t 檢定、變異數分析、線性迴歸
- 無母數分析方法(檢定)：
無法符合有母數分析所設計的方法；
常使用排序(大小順序)取代測量數值，或使用各分類的次數以進行統計分析
代表檢定：Kruskal-Wallis, Mann-Whitney U test

無母數統計方法適用情況：
- 資料類別屬於：類別、順序資料
- 資料==無常態分佈== 或==未知情況==
優點：適用資料不受限制、計算較簡單快速、小樣本下也適用
缺點：不做資料分佈假設可能會損失一些重要資訊，無母數統計方法的檢定力因此會比較弱。
特點：順序尺度資料只能計算中位數（無法計算平均數）因此，無母數統計方法都是檢定中位數而非均數

當要檢定的資料不符合有母數分析法之假設前提時才建議使用無母數分析法，
是一種互補的統計方法，而不適用於取代有母數分析法。

2. 自由度
公式：k-1 (k為樣本數量)

[reference](https://homepage.ntu.edu.tw/~clhsieh/biostatistic/10/10-1-1.html)
[reference](https://www.yongxi-stat.com/kruskal-wallis-h-test/)
[reference](https://estat.pixnet.net/blog/post/61816438-%e7%84%a1%e6%af%8d%e6%95%b8%e7%b5%b1%e8%a8%88%ef%bc%8dkruskal-wallis?utm_source=PIXNET&utm_medium=Hashtag_article)
### 卡方檢定 Chi square test
:small_blue_diamond: 使用時機:

用來檢測觀察到的類別的變量是否與期望的不同，常用的主要有兩個檢定
（目標是檢驗你實際觀察到的數據 是否與你預期看到的不一樣）
1. 卡方適合度檢定（單因素卡方檢定 Test of Goodness-of-Fit）

一個分類變量的==預期頻率與觀察到的頻率相比是否存在著差異==
ex. 想知道骰子骰出來的點數次數是否符合均勻分布
H0：點數出現次數是相等
step 1 : 將類別資料的觀察值次數(O) 列出來
step 2: 一條件要求算出每一格的期望值(E)
step 3:  的觀念，觀察值和期望值差距越小，越接近卡方的值。因為觀察值和期望值越小代表結果越不顯著（符合H0假說）
＊每組數量不能小於5!否則會需要合併

- 實際例子
某家果園依照過去經驗水果產量：芒果：蘋果：水梨為2:3:5，今年水果產量為 28,38,34 (總和為100)

假設H0：今年產量比例與過去相同

算法：
先算出個別的期望值（2/10* 100, 3/10* 100,5/10* 100）得出芒果期望值：20,蘋果：30, 水梨：50
帶入公式可算出x平方～10.45 之後就可以去查表，自由度為（k-1）所以是2，可以發現5.99為臨界值，超過就是拒絕H0，我們可以因此得出：今年的產量和過去產量比例有所不同。

:warning: : 在用這個方法前，研究者必須要決定出某個「已知分佈」，這個已知分佈可能是透過過去經驗、常識、個人推測得出。（像例子中跟去過去的經驗推斷水果產量的比例為何）

2. 獨立性卡方檢定（二因素卡方檢定）

檢測==兩個類別變量之間是否有關係==
ex.想知道心理學 物理學和管理學的學生思維方式是否有差別(學科/思維方式)
H0：思維方式和科系是互相獨立的

3. 同質性檢定 Test of Homogeneity，又稱齊一性檢定

檢定兩個或兩個以上==不同的母體是否具有相同的分配或相同的比例==(不一樣的母群的同一變數是否有不一樣)
ex.不同國家的有無抽煙比例是否相同 （不同母群：不同國家 同一變數：無抽菸比例）/三家不同的便利商店的滿意程度是否具相同比例（不同母群：三家不同的便利商店 同一變數：滿意程度）

---

## 名字：植棻
### Dependency Distance 依存距離

- 一個句子中，兩個語言單位的線性距離 (linear distance)
- 一個字跟他的head之間的關係為 dependency relationship
- dependency distance 越長，表示腦中需要處理的越複雜，也反映句子的 complexity越高


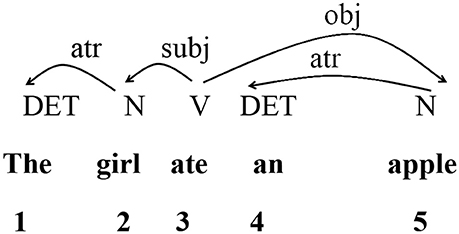
**Hierarchical dependency distance**

- 以 root word 作為最高層級，將 linear dimension 投射為立體的階層結構，一個箭頭為一個層級，多一個箭頭就再往下一個層級

下圖為例：左邊的 root word 是gave，右邊的 root word 是went


Linear DD (X axis) vs. Hierarchical DD (Y axis)


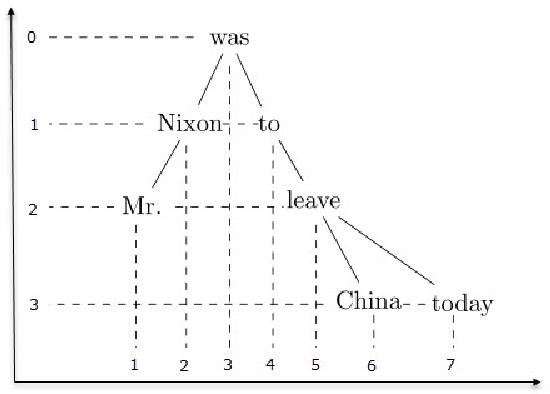
### **Kruskal-Wallis test**

K-W test 是無母數分析，用於比較**多組、非常態分布**的獨立母群體之中位數是否完全相等，也就是這些組別之間的差異大不大。其假設如下：

H0：各組間任兩組的中位數皆相等 (Median1=Median2=…MedianK)
H1：至少有兩組的中位數不相等

K-W test 可以適用的情境如下：

1. 非常態資料
2. 小樣本資料 (N<30)
3. 依變數可以為次序型資料

計算步驟如下：

假設有三組資料，資料A、資料B、資料C，每一組的資料筆數皆為三筆

| A | 3, 4, 5 |
| --- | --- |
| B | 6, 7, 8 |
| C | 2, 2, 5 |
1. 將所有的資料由小至大進行排序

| 組別 | C | C | A | A | A | C | B | B | B |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 資料內容 | 2 | 2 | 3 | 4 | 5 | 5 | 6 | 7 | 8 |
2. 排序後的資料進行ranking，如果遇到資料一樣的，將那幾筆資料的rank 取平均

| 組別 | C | C | A | A | A | C | B | B | B |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 資料內容 | 2 | 2 | 3 | 4 | 5 | 5 | 6 | 7 | 8 |
| Rank | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 平均後Rank | 1.5 | 1.5 | 3 | 4 | 5.5 | 5.5 | 7 | 8 | 9 |
3. 計算各組的rank加總

| A | 3,4,5 | 3+4+5.5=12.5 |
| --- | --- | --- |
| B | 6,7,8 | 7+8+9=24 |
| C | 2,2,5 | 1.5+1.5+5.5=8.5 |
4. 帶入公式計算出H值，並進行檢定
- n 為 樣本數（n=9）
- c 為 組別數（c=3）
- Tj 為 各組 rank 加總（T1=12.5, T2=24, T3=8.5）



進行[查表](https://www.dataanalytics.org.uk/critical-values-for-the-kruskal-wallis-test/)，檢驗H值結果是否顯著。因為資料共有3個組別，因此degree of freedom為2 (3-1)，查表發現 significance level 為0.05且df為2時，其臨界值為5.991，故本範例檢定結果未達顯著。

[Reference_1](https://www.yongxi-stat.com/kruskal-wallis-h-test/)
[Reference_2](https://www.technologynetworks.com/informatics/articles/the-kruskal-wallis-test-370025)

---
## 名字：俞辰
### Chi-Square Goodness of Fit Test (卡方適合度檢定)
卡方適合度檢定是一種統計假設檢驗，用於確定變數是否可能來自指定分佈。它通常用於評估樣本數據是否代表總體。該測試為我們提供了一種方法來確定數據值是否「足夠好」適合我們的想法，或者我們的想法是否有問題。

要將適合度檢定應用於資料集，我們需要：

* 數據值是來自總體的簡單隨機樣本。
* 分類或名目資料。卡方適合度檢定不適用於連續資料。
* 資料集足夠大，以便每個觀察到的資料類別中至少有五個值。

舉例: 假設我們有 10 袋糖果的簡單隨機樣本。我們的分類變數是糖果的口味。每袋有 100 顆糖果。每袋有五種口味的糖果。我們希望每種口味的數量相同。這意味著我們預計每袋每種口味的糖果將有 100 / 5 = 20 塊。對於我們樣本中的 10 袋糖果，我們預計每種口味將有 10 x 20 = 200 塊糖果。這超出了每個類別五個期望值的要求。
根據上述答案，是的，卡方適合度檢定是評估糖果袋中口味分佈的合適方法。

我們會發現我們預計的和實際觀察到的結果之間有差異。為了使實際少於預期的口味與實際多於預期的口味具有相同的重要性，我們將差值平方。接下來，我們將平方除以預期計數，然後將這些值相加就可以得出檢定統計量。

為了得出結論，我們將檢定統計量與卡方分佈的臨界值進行比較。
在統計學中，我們將顯著水準 α 設定為 0.05。除了顯著水準之外，我們還需要找到該值的自由度。對於適合度檢驗，這比類別數少一個。我們有五種口味的糖果，因此我們有 5 – 1 = 4 個自由度。α = 0.05 和 4 個自由度(df = 4)時的卡方值為 9.488 (根據卡方分配表)。

* 檢定統計量低於卡方值。你無法拒絕等比例的假設。您得出的結論是，所有人的糖果袋中每種口味的糖果數量都是相同的。等比例的配合就「夠好了」。
* 檢定統計量高於卡方值。你拒絕同等比例的假設。您不能斷定每袋糖果的每種口味的塊數相同。等比例的契合「還不夠好」。

假設例子中的檢定統計量值為52.75，由於 52.75 > 9.488，我們拒絕糖果口味比例相等的原假設，觀察到的分佈與預期分佈之間的差異具有統計顯著性。

[Reference 1](https://www.jmp.com/en_ca/statistics-knowledge-portal/chi-square-test/chi-square-goodness-of-fit-test.html)
[Reference 2](https://www.scribbr.com/statistics/chi-square-goodness-of-fit/)

### Kruskal Wallis Test
Kruskal-Wallis 檢定是 Mann-Whitney U 檢定的延伸。該檢定為單向變異數分析的無母數類比，用於比較多組非常態分布的獨立母群體之中位數是否完全相等，可偵測到分配位置的差異。該檢定假設作為樣本來源的 k 母群沒有事前排序。

由於Kruskal-Wallis test是無母數方法，適用於以下任3種情境。

1、非常態資料
2、小樣本資料(N<30)
3、依變數可以為次序型資料

Kruskal-Wallis H test的假設檢定一般會寫成：

H0：各組間任兩組的中位數皆相等 (Median1=Median2=…MedianK)
H1：至少有兩組的中位數不相等

K-W 檢定各組樣本數建議至少要5個以上。

下述的範例資料共有三組，實驗組有兩個，控制組一個。

1、將三組人的分數一起進行排序，樣本數分別為n1、n2、n3

這三組樣本分數原始數據排序依序為2、2、3、4、5、5、6、7、8，n1、n2、n3皆為3。

2、將分數從最低(設為rank 1)排至最大(設為rank N)，若有重複的Rank則取平均

3、計算每組的Rank值總和

根據上述表格，我們可以算出各組的排序總和，第一組R1為12.5，接著R2為24，最後R3為8.5，接著進行第四步。

4、計算出H值並進行檢定
Kruskal-Wallis test的檢定值H值公式如下，其中k為組別數，本範例中k為3；ni為第i個群組的樣本個數，本範例中各組皆為3；Ri為第i組的等級總和，本範例中依序為12.5、24、8.5；N為總樣本數，本範例為9人。
將上述數值帶入公式後，我們可以得知

由於H符合卡方分配，而本研究共有3個組別，因此卡方的自由度為2，亦即是k-1。我們接著進行查表，發現當α為0.05且卡方自由度為2時，其臨界值為5.991，故本範例檢定結果未達顯著。

[Reference](https://www.yongxi-stat.com/kruskal-wallis-h-test/)

---
## 名字：靖涵
### **Dependency Parsing**
- Node(節點)): 字(Word)
Edge: 字之間的依賴關係(Dependencies)
- 運用：可以從 dependency parsing 知道句子中不同詞彙之間的句法關係。應用上可以幫助 question answering 和 information extraction 中 **coreference resolution**(指代消解) task ，即可從 dependency parsing 中去解析「代名詞」所指稱的「先行詞」為何者。
- 限制：
1. 每個句子只能有一個 root，通常是句子的核心謂語，且不會有 incoming arcs。
2. 除了 root 以外的 node 皆會有一個 incoming arc。
- 下圖為一句子'I prefer the morning flight through Denver'的 dependency tree example

- Note: 有些演算法會特別強調「**projective**」：即所有圖中的 edges 不可以相交(cross)。

- 產出 dependency tree 有許多不同的 algorithms，例如：
1. **Transition-based approaches**:
- **Shift-reduce Parsing (Arc standard)**:
- 先將句子的每一個詞放在 input buffer，然後讓 parser 決定依序對每一個字要執行那一個動作。parser 可執行的動作有三個：
1. **shift**: 即把 input buffer 的字轉換到 stack 裡面分析
2. **leftarc**: 將 stack 中頂部單字指定為 stack 前一個單字的頭
3. **rightarc**: 將 stack 中前一個單字指定為 stack 頂部單字的頭

以下圖 'Book me the morning flight' 為例，可以見句子的 root 為 book。 依序放入第二個字 me 到 stack，然後 parser 可決定兩者關係，並執行 rightarc，得出 Book -> me。

依序執行最終即可得出單字之間的 dependency relation

- Note: 在這裡 parser 可以分析是要執行三個步驟的哪一個，是因為他已經是不同 treebank 經標記的資料集（例如：Universal Dependency Project） 訓練的監督式模型。
2. **Graph Algorithms**
會把每個字當作一個點，然後用最短路徑算法、動態規劃算法等不同圖算法計算。
- **Maximum Spanning Tree**:
Maximum Spanning Tree 的算法則幫不同字之間的關係評分，然後選曲最終分數最大的關係線。如下圖，藍色線為分數最大化的最終選擇。

[Reference_dependencyparsing_1](https://www.youtube.com/watch?v=2jLk93iIyrw)
[Reference_dependencyparsing_2]()

### **Kruskal Wallis test**

- 使用時機：想看三個或更多獨立樣本之間有沒有差異，且不預設常態分佈。
- Null-hypothesis(H0): 每個群體的中位數、集中趨勢相等，即來自於同一個群體。
- Alternative-hypothesis(H1): 只少有一個獨立樣本的集中趨勢不同，即來自不同群體。
- non-parametric counterpart to single factor analysis of variance (ANOVA)
- Analysis of variance: 計算是使用每個群體的平均值(mean)，看彼此的平均值有沒有差別。
- Kruskal Wallis test: 計算每個群體的排序總和(rank sum)，看彼此的排序總和平均有沒有差別。
- 即不是計算實際的數值，而是把所有群體混合然後排序。
- 優點：data 用排序的方式，可以符合任何的分佈假設。
- Note: Mann-Whitney U test 和 Kruskal Wallis test 相似，但前者是用在兩個獨立樣本時，而後者是用在三個或更多的獨立樣本時。
- expected rank sum 為當所有獨立樣本算出的值相同時的數量。假設現在有三個獨立群裡，每個群體中有4個樣本，共12個樣本。排序後的 exprected rank sum 即為 12(1+12)/2/12=6.5。以下圖更詳細為例，即可進一步計算每一個群體的 排序總和平均 以及 rank variance。

- **Degree of freedom**(自由度)： 以樣本的統計量來估計母體的母數時，樣本中能自由、獨立變化的數據的個數。這裡為組數k扣1，因對每組數據求和，自由度減少，即 k-1。
- 有了以上數值之後即可計算 H，公式如下：

$$H = \frac{{12}}{{N(N+1)}} \left( \frac{{\sum_{j=1}^{k} \frac{{R_j^2}}{{n_j}}}} {{n}} - 3(N+1) \right)$$
- N：總樣本數。
k：組數。
Rj：第 j 個組的總和 。
nj：第 j 個組的樣本數
n： 所有組的總樣本數。

[Reference_kruskalwallistest_1](https://www.youtube.com/watch?v=l86wEhUzkY4)
[Reference_kruskalwallistest_2](https://www.yongxi-stat.com/kruskal-wallis-h-test/)
---
## 名字：予茜
### 句法樹
句子是有階層關係的，通常來說文法是有限的，但是句子是無限的(句法的無限性)。而句法分析主要著重在機器「如何」產生一個**符合文法的句子**。


透過此句法分析可發現，要構成一個句子可能需包含名詞片語(NP)、動詞片語(VP)和而介係詞片語(PP)則可有可無。

[圖源](https://thelp.ithome.com.tw/articles/10295891?sc=rss.iron)

### Dependency Distance 依存距離
* 指的是兩個詞彙在句法上彼此有關聯，兩者的線性距離。
* 可用在分析詞彙（或句子？）的複雜程度。
* 在自然語言的處理當中，會透過句子依存的關係，確定句法的結構或詞彙彼此之間的關聯，常見的分析有兩種：

**第一種**：syntactic structure parsing（句法結構分析）
又稱constituent structure parsing，目標是利用文法結構，產生正確的句法結構樹 (Syntactic Parsing Tree）


句子的意思不一樣，造成句法結構不同。

**第二種**：dependency parsing（依存句法分析）
目標是找到**特定詞彙**在句子中，與其他詞彙的依存關係。
想要進行這個分析必須包含以下兩個條件：

1. 有一個 head 和一個修飾 head 的 dependent 。
2. 根據 head 和 dependent 之間的依賴性質進行標記。

例如：想要看「hit」這個詞和其他詞彙之間的關係。(hit為head，看head和其他dependent之間的關聯)


句子的主要基根(root)是 hit 這個動詞，然後句法分析會看每個token 和 root之間的關聯。

例如：John 就是名詞主語、can 是助動詞、ball 是直接受詞（direct object, dobj）。而 the 在這個句子中和動詞是沒有關聯的，而是跟直接受詞 ball 有關係，the 是 ball 的限定詞（determiner, det）。最後就是標點符號（punctuation, p）。

[圖源](https://ithelp.ithome.com.tw/articles/10295891?sc=rss.iron)
[來源](https://ithelp.ithome.com.tw/articles/10295891?sc=rss.iron)

### Chi-square (卡方檢定)
若針對的是**類別資料**，最常用的分析為卡方檢定。
分成三種：獨立性檢定、適配度檢定以及同質性檢定。

前提：
一，所有的變項為類別變項；二，樣本須為獨立變項→第一組的樣本不影響第二組的樣本；第二組的樣本也不影響第一組。

假設有ａ，ｂ兩個類別。

| | yes | no | total |
| --- | --- | --- | ----- |
| yes | A | B | A+B |
| no | C | D | C+D |
| total | A+C | B+D | A+B+C+D |

公式：

[圖源](https://www.yongxi-stat.com/chi-squared-test-of-independence/)

期望次數的計算是以每行與每列之交乘值除以總數(Total)便得到期望值，例如：[(A+B)*(A+C)]/Total為A 之**期望值**。

觀察值與期望之差異之總和，若差異越**大**則表示兩變數之間**越有關聯性**，越容易**顯著**。

* 獨立性檢定(Test of Independence)
探討在同一個樣本中兩個變數間是否有關聯。也就是討論兩個類別變項(例如：性別和結婚狀態)之間，是否為**相互獨立**，或者是**有相依的關係存在**，若是達到顯著，則需進ㄧ步查看兩個變項的關連性**強度**。

[來源](https://www.yongxi-stat.com/chi-squared-test-of-independence/)

* 適配度檢定(Test of Goodness-of-Fit)
適合度檢定用於分析兩分布的比例是否一致。例如：想要知道抽血血型的分佈比例是否符合台灣人血型的分布，進行**母體**與**樣本**的比較。

例如：

| 血型 | A型 | B型 |AB型 | O型 |
| -------- | -------- | --- | --- | -------- |
| 母體分布 | 25% | 25% | 30% | 20% |
| 樣本分布 | 20 | 30 |30 | 20 |

可得的算式為：

卡方值為「２」時表示是未達顯著，接受虛無檢定。

[來源](https://www.yongxi-stat.com/chi-test-of-goodness-of-fit/)

* 同質性檢定 (Test of Homogeneity)
檢驗二個不同樣本在同一變項的分佈狀況。例如：台北市與新北市的新生兒男嬰與女嬰的分布情形，兩個縣市是否有**類似**的分布模式或是具有**相同**的性別特質。

例２：不同性別對於工作勞累的程度的分布狀況。
自變項：性別( 0男，1女)

依變項：疲勞(為類別變項，0代表沒有感到疲勞，1代表感到疲勞)

[來源](https://www.yongxi-stat.com/chi-test-of-homogeneity/)

---
## 名字：喻璞

### Projection 投影 (線性代數)
在線性代數中，投影（projection）是指將一個向量投影到另一個向量上的過程。在典型的三維正交向量空間內，一個向量的投影到一個平面上一面會是這樣：


通過垂直的方式，我們能將不在某個子空間內的向量轉換為最接近原始向量b的投影向量b，以此來近似原始向量b。投影的計算通常使用向量的內積或者矩陣的乘法來完成。 [Ref](https://face2ai.com/Math-Linear-Algebra-Chapter-4-2/)

#### Random Projection 隨機投影法

隨機投影是一種高效率的「降維」的方法：透過犧牲精度減少資料的維度，以減少處理時間或快速處理小模型。其方法為降低歐幾里德空間中一組點的維度以達到降維效果。

##### 主要理論： Johnson-Lindenstrauss lemma
將高維點低失真嵌入到低維歐幾里德空間的結果。高維空間中的一小組點可以嵌入低維空間中，從而使點之間的距離幾乎保持不變。

##### 高斯隨機投影 Gaussian Random Projection
高斯隨機投影通過將原始輸入空間投影到一個隨機生成的矩陣上來降低維度。

##### 稀疏隨機投影 Sparse Random Projection
稀疏隨機投影通過使用稀疏隨機矩陣將原始輸入空間投影來降低維度。

而稀疏隨機矩陣是一種替代密集高斯隨機投影矩陣的方法，它保證了類似的嵌入質量，同時**更加節省內存並允許更快地計算**投影數據。 [Ref1](https://en.wikipedia.org/wiki/Random_projection) [Ref2](https://scikit-learn.org/stable/modules/random_projection.html)

### Pearson chi-square goodness-of-fit test 卡方適合度檢定/配適度檢定

檢驗你==預期==的出現頻率分佈，是否 **「適合」** 用來描述你的==實際資料==。
利用樣本資驗證母體的分布是否符合特定 ==**機率分布**== 組合。

#### Example
樣本是否與母體類似?
> 讓我們以糖果袋為例。我們隨機抽取十袋樣本。每袋有 100 顆糖果，五種口味。我們的假設是每袋中五種口味的比例是相同的。

#### 假設前提
- 數據值是來自總體的簡單隨機樣本
- 資料來自於同一群體（同一樣本）
- 每次試驗皆屬於**相互獨立**。
- 類別or名目變數。卡方適合度檢定**不適用於連續資料**
- 單因子(one-way)
- **有**預設比例數字
- 資料集需足夠大，以便每個觀察到的資料類別中至少有五個值。

[Ref1](https://www.jmp.com/en_ca/statistics-knowledge-portal/chi-square-test/chi-square-goodness-of-fit-test.html) [Ref2](https://www2.nkust.edu.tw/~tsungo/Publish/12%20Tests%20of%20goodness%20of%20fit%20and%20independence%20powerpoint.pdf)

### 補充：卡方檢定Chi-squared Test
1. Goodness-of-fit test 配適度檢定
如上

2. Test of Homogeneity 同質性檢定
確認不同群體間，類別變數是否有**相同的分佈**
例：不同性別，養貓/養狗/養兔子/不養寵物的比例是否相同
- 資料來自於兩組or多組群體
- 二因子(Two-way)
- 無預設比例數字

3. Test of Independence 獨立性檢定
兩類別變數是否存在**關聯**
如：身高是否超過 170 公分與是否喜歡打籃球的興趣有關
- 資料來自於同一群體
- 二因子(Two-way)
- 無預設比例數字

[Ref](https://haosquare.com/chi-squared-test/#%E9%85%8D%E9%81%A9%E5%BA%A6%E6%AA%A2%E5%AE%9A)

---

## 名字：孟桁
Power Law
A relationship between two variables where one is the exponent of the other. It is a phenomenon widely researched in multiple fields, including probability distributions.

Cumulative Distribution Function (CDF)
CDF describes a running total of probability values.

[Reference] (https://byjus.com/maths/cumulative-distribution-function/#applications)
---

<!-- ## tags, 拜託不要刪除以下 -->
###### tags: `QL2024`

<!-- ---

## 名字：
### 以下如果要用到標題請打三個以上的井字號 -->