:dart: W10 - Generalized Linear-Mixed Model, ANOVA
===

<!-- ## Table of Content
[Toc] -->

## 名字：瓈萱
### Fixed effect 固定效應 /Random effect 隨機效應
- fixed effect

在所有觀察中保持不變的因素,可以控制研究者想要觀察的結果
ex. 有實驗想要觀察五間學校中教學方式對成績的影響，五間學校有各自可能影響學生成績的因素 但是研究者只分析“教學方式（實體/線上）”這個因素對成績的影響，研究者假設且認為這個因素在五間學校中都有影響，因此“教學方式“就是fixed effect ，教學方式的影響也不會因為五間學校內部其他性質的不同而有所改變（A學校一天只有3節課／B學校規定每天都要繳交讀書進度/C學校的老師都是外師..., 不會考慮到"個體" 之間的差異）

計算方式：
依變數：學生考試成績, 獨立變數：教學方法（binary, 實體設為0,線上設為1)
Yi = β0 + β1X + εi
在上面舉的例子當中 Yi 代表學生的分數，β0 是截距，X是教學方法的變量，β1 是教學方法變量的係數，εi 是誤差項。
如果β1＝16 的話就代表 比起線上模式教學方法比實體高出16分，這個結果在五間學校都是一至的（學生使用線上上課的成績會比實體上課的成績高，而每所學校都是這樣）

- Random effect

不去預設什麼可能影響什麼，把所有可能影響的變因都考慮進去 結果可以更好的知道什麼因素可能會影響到某個結果，也可以很好的用來捕捉研究者他們没有直接觀察的因素，但这些因素可能会對研究結果有影響
隨機效應的目的之一就是捕捉这些未被觀察到的因素對實驗結果的影響，以减少因未考率到這先因素的原因造成結果上有所偏差，除此之外他也會把個體之間的差異（ex. A學校的師資都是外師）考慮進去

- fixed effect / random effect 之間的差異

fix effect 是已經預設什麼了A原因（教學方式）可能會造成B結果（學生成績有差）而且這種影響是固定的（每間學校都一定會有影響）研究者可以更好的去理解它們想觀察的變因對結果的差別或影響 (研究者只想去了解教學方式跟學生成績之間的關聯，所以就只考慮這兩個因素，並不會去考慮學校內部各自可能影響學生成績的原因。），而random effect 則是去看所有可能影響原因 造成的改變或影響

- mixed effect model

就是將fixed effect 跟 random effect 都納入考慮， 除了看全體的影響 也將個體之間的差異也考量進去。 比如說想研究學生成績如何受到教學方式、和學校差異的影響，固定效應部分考慮了教學方法對整個樣本的影響（所有學校皆會受影響），而隨機效應部分則考慮了不同學校之間的差異，例如學校的師資水平、學校規模等因素對學生成績的影響。通過將這兩種效應結合起來，混合效應模型能夠更全面地解釋學生成績的變化，並提供更準確的估計。

[reference](https://medium.com/@akif.iips/understanding-random-effect-and-fixed-effect-in-statistical-analysis-db4983cdf8b1)
[reference](https://web.ma.utexas.edu/users/mks/statmistakes/fixedvsrandom.html)
### Stepwise regression 逐步回歸

結合了線性迴歸＋逐步挑選（Selection）兩種演算法的一種方法。當我們想要建立一個線性迴歸模型，並且希望知道哪些特徵最適合放入模型 可以獲得最佳表現時，就可以使用step regression。這種方法通過反覆添加或移除某些特徵，並利用檢定來評估模型的表現，最終找到最佳的模型。
- forward selection

將變數依序放進模型中，如果A變數放入模型具有顯著性，就繼續放著。接著會下一個變數去測試，重複的步驟直到變數對模型結果不具有解釋力（顯著性）為止


- backwards slection

反向淘汰法則是一開始將k個變數直接放到模型中，依照一些標準去淘汰對模型解釋力最小的變數（低顯著），對結果最沒影響變數。重複這個步驟直到所有變數都是對結果有所影響的。


- stepwise regression analysis
Forward Selection 與 Backward Selection 的綜合體。先選出影響最大的變數，再從中把解釋力小的變數拿掉，一直重複這個動作，直到模型表現最佳為止。

[reference](https://ods.tmu.edu.tw/portal_c3_cnt.php?owner_num=c3_71137&button_num=c3&folder_id=4614)
[reference](https://medium.com/ntu-data-analytics-club/%E7%94%A8-r-%E4%BE%86%E5%AE%8C%E6%88%90%E9%80%90%E6%AD%A5%E5%9B%9E%E6%AD%B8%E5%88%86%E6%9E%90%E6%B3%95-f4e1158eb2ed)
[reference](https://www.cupoy.com/qa/collection/0000017705894B9C000000036375706F795F72656C656173654355/00000177151DDEC3000000236375706F795F70726572656C656173654349/0000017F2E7824A80000000B6375706F795F72656C656173655155455354)

### Language Accomadation
在與他人交談的時候，因為某些原因改變自己平常的說話模式。改變的方式有兩種
- convergence語言趨同
因為對話者的身份、社會地位、年齡、性別或為了在群體中得到認同等社會因素讓我們不自覺得跟別人講話的方式變得一樣
- divergence 語言趨異
為了強調自己跟別人不一樣 所以可意在講話的時候讓自己特別不一樣 (可能是為了顯示自己的社會地位)
ex. 新加坡人講話卻故意捲舌、或者是跟中國人講話偏偏每個捲舌音都故意不發
[reference](https://uegu.blogspot.com/2014/11/blog-post_28.html)
---

## 名字：俞辰
### Poisson Distribution (帕松分佈)
帕松分佈適合用於描述單位時間內隨機事件發生的次數的機率分佈。如某一服務設施在一定時間內受到的服務請求的次數，電話交換機接到呼叫的次數、汽車站台的候客人數、機器出現的故障數、自然災害發生的次數、DNA序列的變異數、放射性原子核的衰變數、雷射的光子數分佈等等。

帕松分佈適用於條件如下:
1. 事件彼此獨立。(這前提超重要喔顆顆)
2. 事件發生的平均頻率為持續發生的。
3. 兩個事件不能同時發生。

泊松分配是觀察k事件在一段時間發生時，給定發生週期，看單位時間內平均的發生頻率的機率。公式如下

[Reference](https://https://xiaoxiaosam007.medium.com/poisson-%E6%B3%8A%E6%A1%91%E5%88%86%E9%85%8D%E7%9A%84%E5%AF%A6%E4%BE%8B%E5%88%86%E6%9E%90-723bda5262e2)

### ANOVA
單因子變異數分析 (ANOVA) 是一種用於檢定三種以上群組平均數差異的統計方法。當您有單一獨立變異數或因子，且目標是查證變異數或不同程度的因子是否對應變數造成可衡量的影響時，可以使用單因子變異數分析 (ANOVA)。比較三個或多個群組的平均數時，此方法可以告訴我們是否至少有一對平均數存在顯著差異，但無法告訴我們是哪一組平均數有差異。此外，各群組的應變數也必須為常態分佈，且各群組的群組內變異性必須相似。

單因子變異數分析是一種檢定虛無假設的統計方法 (H0)，此虛無假設假設三個或以上的母體平均數相等，而替代假設 (Ha) 則是至少有一個平均數不相等。k 個平均數的統計假設形式符號寫法為：
而 μi是 第i 群組因子的平均數。

變異數分析主要是用來檢定多組相互獨立樣本的母體平均數是否具有顯著差異，也就是說，樣本的母體變異數必須具有同質性。

因此，在進行變異數分析之前，我們會先進行樣本母體變異數的同質性檢定，若各樣本的母體變異數皆具有同質性，就可以使用變異數分析來進行之後的檢定。

變異數分析的概念與方法
在做變異數分析時，我們需要先知道兩種樣本變異的資訊：

●組間變異(Between-group variation)：不同組樣本之間的資料變異程度
●組內變異(Within-group variation)：各組樣本本身資料間的變異程度

得到樣本的變異資訊後，就可以利用組間變異與組內變異的相對大小來檢定不同組樣本之間母體平均數的差異。當組間變異越大，組內變異越小時，拒絕虛無假設H0的機率就越高，也就表示被比較的各組樣本，其中至少有一組樣本的母體平均數與他組樣本的母體平均數有著顯著的差異。

[Reference 1](https://www.jmp.com/zh_tw/statistics-knowledge-portal/one-way-anova.html)
[Reference 2](https://yourgene.pixnet.net/blog/post/118650399-%E8%AE%8A%E7%95%B0%E6%95%B8%E5%88%86%E6%9E%90anova)

### Bonferroni Correction
Bonferroni 校正是在對單一資料集同時執行多個相關或獨立統計檢定時對 P 值的調整，是一種多重比較校正方法，用於調整統計分析中的顯著性水平，以降低因多次檢驗而產生的偽陽性錯誤（Type I錯誤）的可能性。這種校正方法通常應用於進行多個統計檢驗或比較的情況下，例如在進行多組間比較或多個變數的比較時。通過將顯著性水平除以進行檢驗或比較的總數，Bonferroni校正確保了整體的顯著性水平不會超出預定的水平，從而避免了額外的偽陽性結果。若要進行Bonferroni校正，請將臨界 P 值 (α) 除以進行的比較次數。 例如，如果正在測試 10 個假設，則新的臨界 P 值將為 α/10。然後根據修改後的 P 值計算研究的統計功效。
Bonferroni 校正的公式為p*(1/n)，其中p為原始閾值，n為總檢定次數。如果像我們舉的例子一樣，原始的P值為0.05，檢驗次數為10000次，那麼在Bonferroni 校正中，校正的閾值就等於5%/ 10000 = 0.000005，所有P值超過0.00005的結果都被認為是不可靠的。

[Reference1](https://docs.ufpr.br/~giolo/LivroADC/Material/S3_Bonferroni%20Correction.pdf)
[Reference 2](https://zhuanlan.zhihu.com/p/51546651?utm_id=0)

---
## 名字：靖涵
### Generalized Linear-Mixed Models (GLMMs)

- **迴歸分析(Regression Analysis)：** 分析變數之間(自變數與依變數)的關係。簡單的線性迴歸 (Simple regression analysis) 即用一個自變量(x)預測一個依變量(y)。
- 因變量 Dependent variable = 反應量 response variable = 結果變量 outcome variable;
- 自變量 independent variable = 預測變量 predictor variable = 解釋變量 explanatory variable = 共變量 covariate.
- **線性迴歸(Linear Regression)** 的 assumptions:
1. 變數**常態分佈**(normally distribution)
2. 變數彼此獨立(independent)
3. Coefficient 需呈線性(linear)
- **Linear Models 線性模型** vs. **Generalized Linear Models 廣義線性模型 (GLM)**
最大的不同為第一點，不同於 linear regression 需要變數為常態分佈，GLM 中資料可以不是 normal distribution ，例如：指數分佈家族 (the Exponential Family of distributions)。
- **Poisson distribution(卜瓦松分布**)：
即為指數分佈家族中的一種分佈。
描述一個時間區間裡面，隨機事件發生的機率分佈。例如：生產線上的疵品數、每小時地震的次數。
特色包含: (1) 短時間內發生兩次以上的機率可以忽略 (2)不重疊的時間段裡面，事件發生次數獨立。

另外，兩者不同的地方還有找到 Coefficient 的 β的方法， linear regression 可以使用 最小平方差(least square) 或 maximum likelihood 找，因為在常態分佈下 maximum likelihood 計算出的結果會跟 最小平方差相同。而在 GLM 的情況下就需要用 maximum likelihood。

- **廣義線性模型 Generalized Linear Models (GLM)** ：延伸傳統線性迴歸模型，可以處理非常態分佈的資料。其中一個特色為，使用 鏈結函數(Link function) 以確保所計算出來的 μ值有意義，將線性模型的預測變量與實際的響應變量關聯起來。而不同的分佈所採用的 link function 也會有所不同，二項式分布 (Binomial distribution) 或 伯努利分布(Bernoulli distribution) 常用 logit 。

不同於 GLM 只考慮 fixed effect ， LMM 同時考慮 Fixed effect 和 Random effect。

- **Linear Mixed Model 混合線性模型 (LMM)**
mixed：即混合了 fixed effect (固定效果)和 random effect (隨機效果)。
- Fixed effect vs. random effect
兩種處理 factor 的方法
- **fixed effect (固定效果)**：重複該研究時，可用同樣分類標準（例如：年齡、性別），這一部分是研究感興趣的地方。
- **random effect (隨機效果)**：重複該研究時，可以用不一樣的分類標準（例如：前測所得到的成績），較不是研究感興趣的地方。

LMM 可以用在有不同層次結構、重複測量數據的情況，考慮不同層次上的相關性，但主要處理連續型因變量和高斯分佈的數據。

- **Generalized Linear-Mixed Models 廣義線性混合模式 (GLMMs)**
GLMM 可視為 GLM 的擴展， 且和 LMM 一樣同時考慮 fixed effect 和 random effect，但不同於 LMM 主要處理連續型因變量和高斯分佈的數據，GLMM 可以處理更多更廣泛的數據結構。

[Reference_simple_regression](https://www.yongxi-stat.com/simple-regression-analysis/)
[Reference_LMM](https://www.yongxi-stat.com/lmm/)
[Reference_GLMM_1](https://www.youtube.com/watch?v=98mYx2Pa74k)
[Reference_GLMM_2](https://blog.csdn.net/fjsd155/article/details/88360671)
[Reference_GLM](https://www.youtube.com/watch?v=ddCO2714W-o&list=PLJ71tqAZr197DkSiGT7DD9dMYxkyZX0ti)
[Reference_Poisson](http://episte.math.ntu.edu.tw/applications/ap_poisson/index.html)

### Overdispersion（過度離散）
overdispersion 為 Poisson distribution(卜瓦松分布) 常見的問題之一。
- Poisson distribution 的 assumption 包含：
1. mean = the rate
2. variance = the rate
-> mean = the variance, the standard deviation = the root of rate (rate 開根號)

所以過度離散是指在 poisson distribution 中發現 **變異數(variance)大於均值(mean)**
-> more variability than expected

- 可能導致 overdispersion 的原因：
1. model 沒有很好的代表(lack a fit)出 observed data 的關係 (missing an interaction)。
2. 太多的 0 (excessive zero)
- 常見解決過度離散的方法：
**negative binomial regression**：和 Poisson distribution 相似，但是 rate, mean, 和 variance 的計算會是分開的，不會像 Poisson distribution 一樣只有一個 parameter 變異數一定要等於均值，所以比較不受限。

[Reference_overdispersion_1](https://www.google.com/search?q=Overdispersion&oq=Overdispersion&gs_lcrp=EgZjaHJvbWUyCQgAEEUYORiABDIGCAEQRRg7MgcIAhAAGIAEMgcIAxAAGIAEMgcIBBAAGIAEMgcIBRAAGIAEMgcIBhAAGIAEMgYIBxBFGD2oAgCwAgA&sourceid=chrome&ie=UTF-8#fpstate=ive&vld=cid:f332766f,vid:0W5QF_OnR7w,st:0)

---
## 名字：植棻
### Poisson distribution

Poisson distribution 是一個機率分佈，會用到的情境是在某時間區段內(*k*)，平均會發生若干次「事件」(λ)，例如：每小時服務台訪客的人數，每天家中電話的通數，一本書中每頁的錯字數，某條道路上每月發生車禍的次數…等等。而事件發生的次數是不一定的，因此「事件」是一個隨機變數，其所對應的機率函數稱為 Poisson 分佈。

一個 Poisson 過程有三個基本特性：

1. 在一個短時間區間 內，發生一次事件的機率與 時間成正比
2. 在短時間內發生兩次以上的機率可以忽略
3. 在不重疊的時間段落裡，事件各自發生的次數是獨立的。


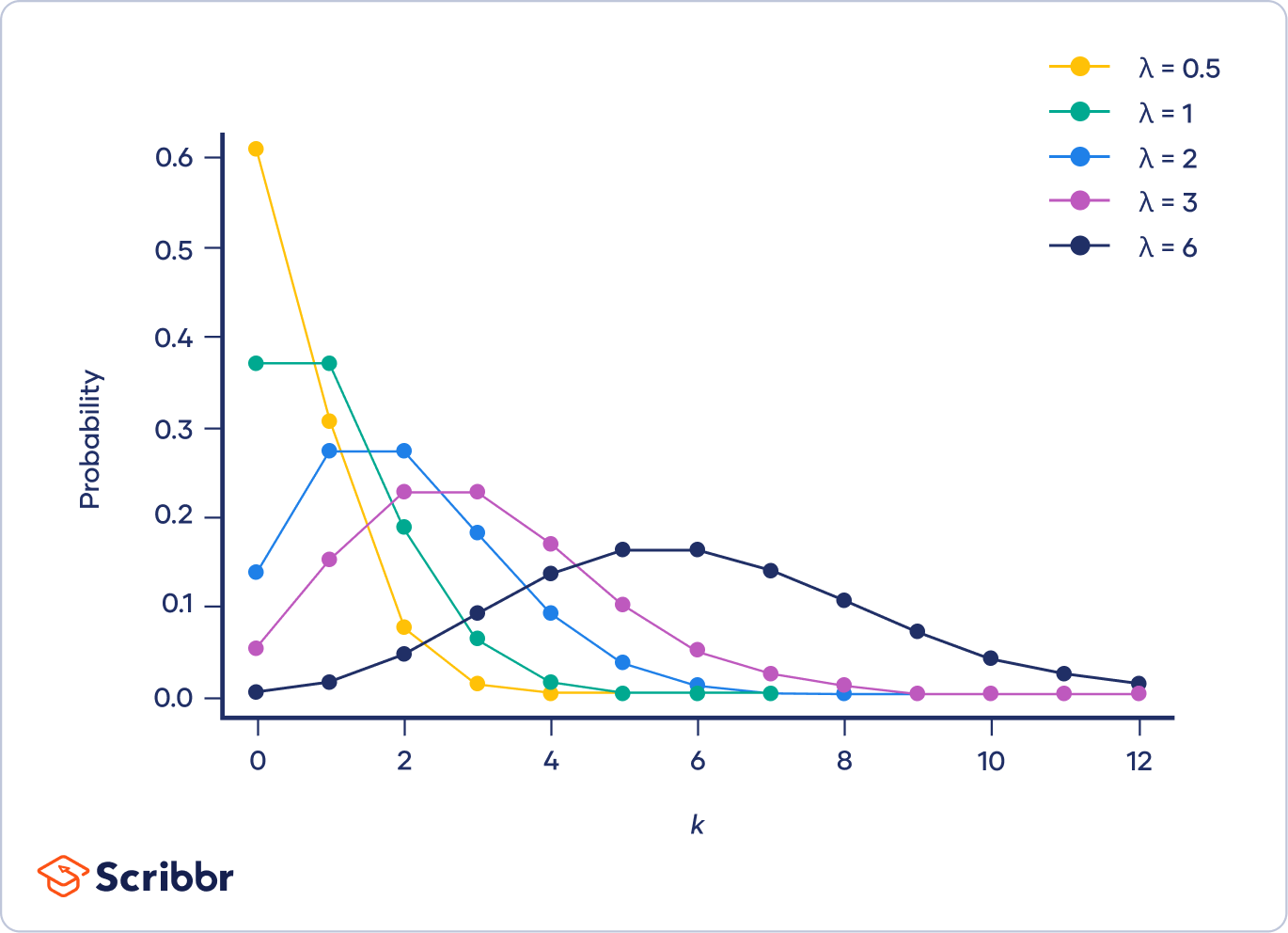
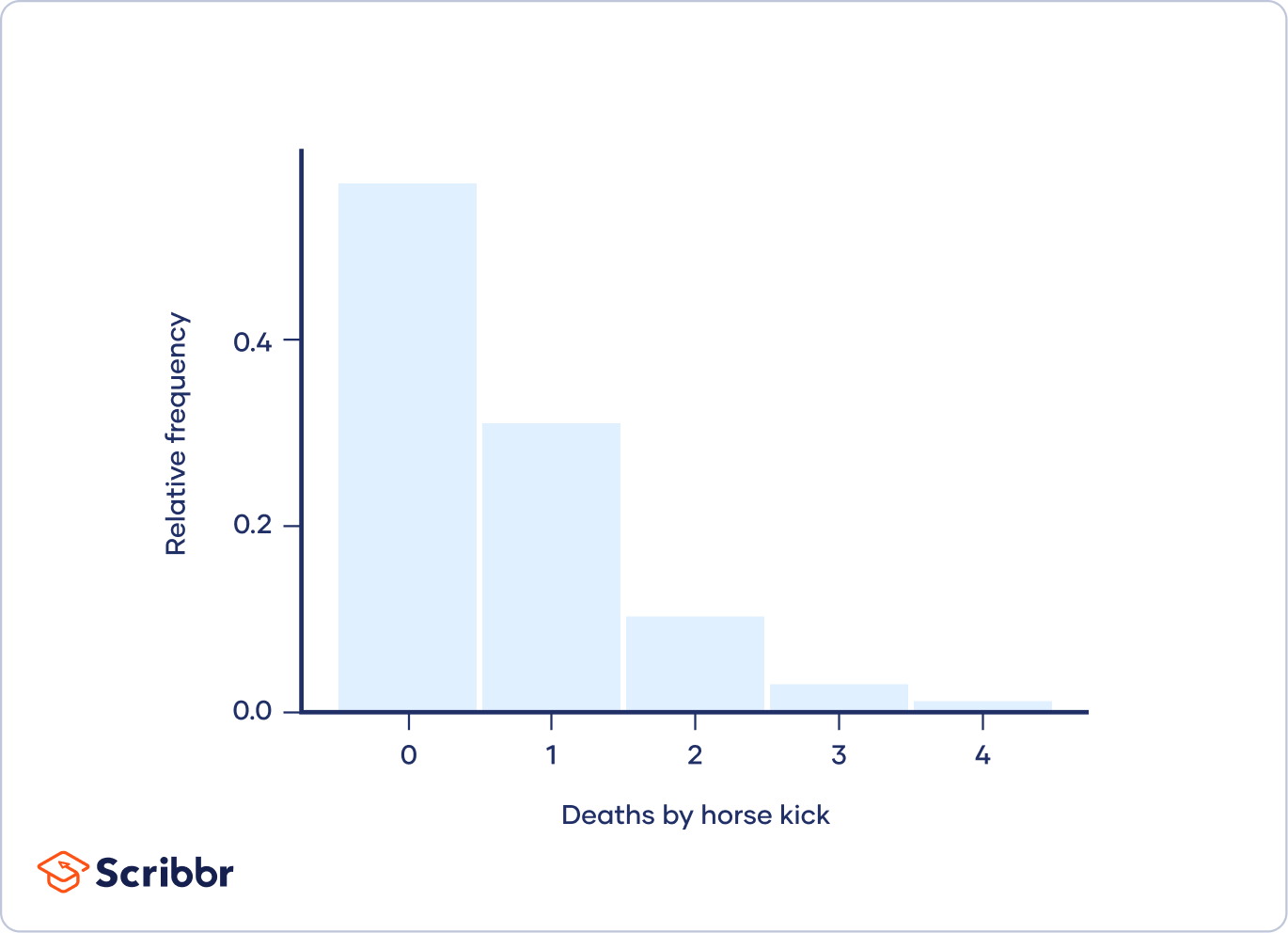
第一個柏松分佈應用的例子是在1800年代末，一位統計學家想要統計軍隊中，軍人被馬給踢死的意外有多有多常發生。經過統計發現平均大約是一年有0.61個軍人被馬踢死。但事實上數據顯示大部分一年當中並不會發生一件這樣的意外，但有幾年會剛好發生多次這個意外。


[Reference_1](https://www.scribbr.com/statistics/poisson-distribution/)
[Reference_2](http://episte.math.ntu.edu.tw/applications/ap_poisson/index.html)

### ANOVA (Analysis of variance) 變異數分析

又稱為方差分析。ANOVA是用於比較**三個或更多**不同組的**均值**之間是否存在差異。

在不同的情況下，有不同的變體可以使用：

- 單因子變異數分析（One-way ANOVA）
- 雙因子變異數分析（Two-way ANOVA）
- 多因子變異數分析（Factorial ANOVA）
- Welch的F檢定變異數分析（Welch’s F-test ANOVA）
- 排名變異數分析（Ranked ANOVA）

**單因子變異數分析 (One-way ANOVA)**

- 只有**一個自變項** (independent variable) ****的變異數分析。
- **獨立樣本** (Independent sample)

例如：比較青年、中年、老年三個年齡層的族群，對於飲料甜度的喜好是否不同。

++**前提假設**++

1. 自變數為**類別變數** (categorical variable)**，**依變數必須是**連續變數** (continuous variable)
2. 母群體必須是**常態分佈** (Normal Distribution)
3. 3**獨立事件** (Independent event)：樣本須為獨立變項，不同組別的樣本互不影響
例如：分析從日本、美國兩地進口的蘋果與台灣當地的蘋果甜度是否有差異，從日本或美國進口與台灣當地的蘋果這三組樣本量測不會互相影響
4. 變異數 (variance) 同質性：兩組樣本的變異數必須**相等**

++**使用情況**++

*婚姻狀況（單身、已婚、離異、喪偶）是否影響情緒？*

這個問題只有**單一的自變量（婚姻狀況）** 還有4組數據（單身、已婚、離異、喪偶）每組的婚姻狀況都有 **情緒分數（因變量）** 作為回答，我們想看的是各組的平均數之間是否有差異。

ANOVA可以協助確認其中哪一組 **婚姻狀況（自變量）** 與 **情緒（因變量）** 有關係。

這裡要注意的是，變異數分析只會顯示所有組別的平均情緒分數是否一樣。看不出來哪一組的平均情緒分數明顯更高或更低。

++**變異數分析分為三種型態**++

- **固定效應模式（Fixed-effects models）**

用於變異數分析模型中所考慮的因子為固定的情況，換言之，其所感興趣的因子是來自於特定的範圍。

例如：要比較五種不同的汽車銷售量的差異，感興趣的因子為五種不同的汽車，反應變數為銷售量，該命題即限定了特定範圍，因此模型的推論結果也將全部著眼在五種汽車的銷售差異上，故此種狀況下的因子便稱為固定效應。

- **隨機效應模式（Random-effects models）**

因子變異數分析所推論的並非著眼在所選定的因子上，而是推論到因子背後的母群體

例如：藉由一間擁有全部車廠種類的二手車公司，從所有車廠中隨機挑選5種車廠品牌，用於比較其銷售量的差異，最後推論到這間二手公司的銷售狀況。因此在隨機效應模型下，研究者所關心的並非侷限在所選定的因子上，而是希望藉由這些因子推論背後的母群體特徵。

- **混合效應模式（Mixed-effects models）**

此種混合效應絕對不會出現在單因子變異數分析中，當雙因子或多因子變異數分析同時存在固定效應與隨機效應時，此種模型便是典型的混合型模式。

[Reference_1](https://www.yongxi-stat.com/one-way-anova-indenpedent/)
[Reference_2](https://www.qualtrics.com/hk/experience-management/research/anova/)

## 予茜
### Generalized Linear Mixed Model 廣義混合線性模型 (GLMM)

建立在**線性回歸**的基礎之上，用於製作**類別**型的預測，應變數為連續型資料，且資料為常態分佈。

**Mixed Model** 混合模型的特徵(混合兩種效應):
1.固定效應:別人若要複製你的研究，則別人可以**同樣**的分類標準來分類，例如性別、年齡及教育程度，即推論是來自於目前的分類標準，通常就是*研究中要探討的變項*。

2.隨機效應:允許別人有不同分類標準的變項，在重複量測中，通常個案即是隨機變項，代表允許每一位個案的初始值可以不同。

**Generalized estimating equation**廣義估算程式(GEE):
1.屬於半母數的統計方法，適用在類別或數值的資料
2.不適合用隨機效應

**GLMM** 廣義線性模型的特徵:
1.改善混合模型僅能處理**連續**型資料的缺失。
2.當數據為**類別**型資料，又附帶**隨機**效果時，便會使用 GLMM。

[reference](https://www.yongxi-stat.com/lmm/)

**迴歸模型**
X與Z分別為獨立變項矩陣，β代表固定效應的常數，γ代表隨機效應的隨機向量，ε為誤差項。

在混合線性模式之中，我們可以透過假設X跟Z**共變異數矩陣**以解釋**重複**測量之間的關係。

前提假設：重複測量研究

[reference](https://www.yongxi-stat.com/lmm/)

---
## 名字：孟桁
### Fixed effect & random effect 固定效應 / 隨機效應

With fixed effects, datasets are assumed to have 1 true underlying effect size, while random effects, being the opposite of fixed effects, assumed varying tendencies to individual datasets.

Both statistical methods can be applied to the same dataset, producing potentially different results depending on the model. Generally, fixed effects are considered when analyzing a small sample size, but random effects are usually the more recommended model.

[reference] (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC9393987/)

### Generalized linear mixed models (GLMM) 廣義線性混合模型

GLMM can be viewed as extensions to the concepts of generalized linear models (GLM) and linear mixed models (LMM).

Compared to a regular linear model which assumes normal distribution in its samples, GLM allows for a wide variety of distributions to its variables, including normal, Poisson, binomial…etc. Also, regular linear models include either a fixed effect or a random effect to present data, but with a LMM both effects are incorporated together.

GLMMs include both fixed and random effects like LMMs, and can be extended to non-normal distribution datasets like GLMs.

---
## 名字：喻璞
### generalized linear-mixed models (GLMMs) 廣義線性迴歸

廣義線性模型是傳統線性模型的延伸，應變數可透過指定的鏈結函數與因數和共變數成線性相關。

LMM 只能適用與因變量爲連續型變量的情況 → GLMM 將線性迴歸模型拓展到因變量可以使用二分類，計數，分組型變量的建模工具。

GLMM 允許因變量具有非正態分佈。

y - response variable / 響應變量 / 應變數
x - explanatory variable / 解釋變數 / 獨立變數

#### link function
廣義廣義線性模型(GLMM) 會包含 鏈接函數 (link function)，它將響應的期望值與模型中的線性預測因子相關聯。這個鏈接函數的作用是將分類響應變量的各個水平的概率轉換為一個連續且無界的尺度。

#### 數據類型
適用於尺度(scale)、計數(counts)、二元(binary)或試驗中的事件(events-in-trials)等資料類型。 [ref](https://support.minitab.com/zh-cn/minitab/help-and-how-to/statistical-modeling/regression/supporting-topics/logistic-regression/link-function/)

[ref1](https://bookdown.org/ccwang/medical_statistics6/section-44.html)
[ref2](https://www.ibm.com/docs/en/spss-statistics/saas?topic=statistics-generalized-linear-models)

### observation-level random effect (OLRE)
觀察水準隨機效應 (OLRE) 是每次觀察值是否具有不同程度的隨機效應。當與Poisson distribution結合使用時，OLRE可以幫助捕捉適度的過度離散性，可以考慮到模型額外的變異性、獲得更準確的估計和更好的模型擬合。

[ref](https://rstudio-pubs-static.s3.amazonaws.com/192342_57c802f98a5e4d7d8fc337ca384d6932.html)

### Bonferroni 邦弗朗尼校正

邦弗朗尼校正是透過對 P 值進行調整，解決多重檢定問題的一種方法。

#### What is 多重檢定問題？
當我們做越多次的假設檢定，越有可能單純因為隨機性而錯誤地拒絕虛無假設。

#### Bonferroni 校正計算方式
當研究中同時進行多個統計檢驗時，存在著產生偽陽性結果（類型 I 錯誤）的風險。Bonferroni 校正的目的是降低這種風險，以確保結果的可靠性。

##### 錯誤：產生多重檢定問題
假如顯著性水平為 0.05，如果同時進行了 20 個統計檢驗，新的顯著性水平將為 0.05/20，即 0.0025。變成每一個單獨的統計檢定中，p-value < 0.0025 時才被視為顯著。

##### 正確 (Bonferroni 校正)
例如，一位研究人員同時測試 20 個假設，臨界 P 值為 0.05。在這種情況下，以下是正確的：
P（至少有一個顯著結果）= 1 - P（沒有顯著結果）
P（至少有一個顯著結果）= 1 -（1-0.05）^ 20
P（至少有一個顯著結果）= 0.64

[ref1](https://www.google.com/search?q=Bonferroni+adjustment&sca_esv=3eb2b7adee194e22&rlz=1C5MACD_en__1030__1030&sxsrf=ACQVn0_XenCmPGaJlopvuQhzcFPIgiJBYQ%3A1714048617478&ei=aU4qZvDgHImevr0Px6GO-As&ved=0ahUKEwiwuePXsN2FAxUJj68BHceQA78Q4dUDCBA&uact=5&oq=Bonferroni+adjustment&gs_lp=Egxnd3Mtd2l6LXNlcnAiFUJvbmZlcnJvbmkgYWRqdXN0bWVudDIFEAAYgAQyCBAAGIAEGMsBMggQABiABBjLATIIEAAYgAQYywEyCBAAGIAEGMsBMggQABiABBjLATIIEAAYgAQYywEyCBAAGIAEGMsBMggQABiABBjLATIIEAAYgAQYywFIugdQ-ARY-ARwAXgBkAEAmAFIoAFIqgEBMbgBA8gBAPgBAvgBAZgCAqACUcICBxAjGLADGCfCAgoQABiwAxjWBBhHmAMAiAYBkAYKkgcBMqAHuQQ&sclient=gws-wiz-serp) [ref2](https://haosquare.com/multiple-testing-intro/)

---

<!-- ## tags, 拜託不要刪除以下 -->
###### tags: `QL2024`

<!-- ---

## 名字：
### 以下如果要用到標題請打三個以上的井字號 -->