---
header-includes:
- \hypersetup{colorlinks=false,
allbordercolors={0 0 0},
pdfborderstyle={/S/U/W 1}}
title: "Quantum computing lecture notes"
author: "Kev M. Salikhov"
output:
beamer_presentation:
includes:
in_header: header_pagenrs.tex
---

Other documents:
- [lecture notes 6-7](https://hackmd.io/O6ma0fRTSFeGJSXiRggZJw)
- [exam questions](https://hackmd.io/scEdk-W0SaeiyujSYtHMpQ)

# Quantum computing lecture notes (1-5)
20.08.2021

### Plan for the course:
- QC from the top, comparison to classic, additional resources of QC
- Postulates of QMechanics
- Examples of computing given electron spins as qubits
- Examples of Quantum Algorithms
- Error correction
- On implementation of QComputers
- perspectives of QC

---

## Lecture 1. What is QC, what is quantum computer in general

---

### **Classic computers** start from A. Turing (math model).
- [Turing Machine](https://en.wikipedia.org/wiki/Turing_machine) is a mathematical model of a physical system (a ribbon).
- Any information can be coded in 2-state gates.
- *Bit* is a term for amount of information, but often we can *bit* a gate itself.
- *NOT* and *[Controlled-NOT](https://en.wikipedia.org/wiki/Controlled_NOT_gate) (CNOT)* [quantum] gates are enough to implement any classic program.
- There are also [qutrits](https://en.wikipedia.org/wiki/Qutrit) for 3-state systems. They can sometime be beneficial, but not developed that much.
- First classical computer was developer 1941 ~18000 vacuum tubes, 30 tons. Used [relays](https://en.wikipedia.org/wiki/Relay) (before transistors appeared)
- Anything spoken in words can be coded in classical computer... But we need more memory!

---

### **Microrelectronics**
- Revolution started with semiconducting diodes of ~$\mu m$ ($10^{-4}$) size.
- How to create a gate: bomb Si with Fe+ to create ferro-magnetic "lakes" which can have magnetic momenum, controlled by outer force

---

- We can have $10^8$ gates per $cm^2$, but at nano scale ($10^{-9}$ linear sizes) world changed. Refer to [Feynmans lecture "There's Plenty of Room at the Bottom"](https://en.wikipedia.org/wiki/There%27s_Plenty_of_Room_at_the_Bottom).

---

### **From classic to quantum**
- qubit = "quantim bits". We can have macroscopic objects which have quantum properties, e.g. superconductor's conductivity.
- it is hard to address qubits selectively, if they are small. That is why most promising approach is using supercondictors. BUT them we will loose memory capacity!
- For QC it is enough to have ~500 gates to solve any "imaginable" problem. <100 gates are enough to solve almost any.
- This doesn't mean we should stop searching other implementations.
- transition: even if qubit can also be **observed** as a 2-state system, it **has** infinite number of states.

---

### Quantum:
- basic operations are NOT and **C-NOT**: if A then not B.

| IN | OUT|
| -- | -- |
| 00 | 00 |
| 01 | 01 |
| 10 | 11 |
| 11 | 10 |

- States - any vector from [Hilbert space](https://en.wikipedia.org/wiki/Hilbert_space). E.g. we usually denote

$|0\rangle = \begin{pmatrix}1 \\ 0\end{pmatrix}$

$|1\rangle = \begin{pmatrix}0 \\ 1\end{pmatrix}$

---

- NOT in matrix form:

$NOT=\begin{bmatrix}0&1\\1&0\end{bmatrix}$

$\begin{pmatrix}0 \\ 1\end{pmatrix}=|1\rangle=\begin{bmatrix}0&1\\1&0\end{bmatrix}\times|0\rangle = \begin{pmatrix}1 \\ 0\end{pmatrix}$

---

### **New resources of QC**
- 1 qubit ~ $\psi = a|0\rangle+b|1\rangle$, where $|a|^2+|b|^2=1$;
- 2 qubit ~ $\psi = a|00\rangle+b|01\rangle+c|10\rangle+d|11\rangle$;
- N qubits - $2^N$ coefficients
- System can occupy multiple basic states at the same time.
- QC allows to perform logical operations, which cannot be implemented by classic computers, e.g. $\sqrt{NOT}$
- Cross terms: $a*b$ (coherence) increase faster, then just a number of coefficients. They are the major carrier of information in QC.

---

### Problems of quantum computers:
- !! systems are loosing their properties with time.
- quantum coherence disappears with time! Major information is stored not in a [population](https://physics.stackexchange.com/questions/235069/what-does-population-mean-in-regards-to-the-excited-and-ground-states-of-an) of states (probability to observe a state).
- system evolution needs time. E.g. apping NOT and stopping earlier will not result into "pure NOT". In math this is just a unitary matrix multiplication
- Memory comparison: 48 qubits are "equivalent/comparable" to $10^{14}$ classic elements ($1cm^2$ with $nm$ scale).
- quantum systems cannot be copied. If we can reproduce a system -- we destroy initial state

---

### How can we build a qubit
- Actually any quantum system.
**QD**
- [quantum dot](https://en.wikipedia.org/wiki/Quantum_dot). Potential box for an electron. We choose any pair of states of an $e^-$ as a calculation basis, e.g. $n=0,1$. If states were equidistant, we could excite it even further ($n=2$). But as energy level of electron are not equidistant, we are ok.
- We should be sure we address only 2 states and only them. 2 states -- is just a metter of convenience, as everything is already binary.
- Using [Fullerene](https://en.wikipedia.org/wiki/Fullerene) with Nitrogen ($N$) inside was proposed.

---

**Spin**
- [Electron spin](https://en.wikipedia.org/wiki/Spin_(physics) )! Just an electron has magnetic moment (no wires, no other). $\omega=\gamma B_0$
$|+\frac{1}{2}\rangle =>|1\rangle$. Proton also has spin.
- Why? 1944 Zavoisky developed [EPR](https://en.wikipedia.org/wiki/Electron_paramagnetic_resonance) to do whatever we need with electron spins.
- Irradiated malonic adic. Detach one $H^+$. You have an electron with $1\mu s$ decoherence time. We can have order of ten operations. Not too much.

---

**Dimond defects**
- In diamond we replace one C with N. Loss of electron.

**Biradicals**
- CNOT with 2 unpaired electrons. We need intereaction between spins, e.g. inside a molecule.

- concept of [coherence](https://en.wikipedia.org/wiki/Coherence_(physics) ) is the major concept to learn for the future.

---

*Q&A*:
- Why do you thing Schrödinger equation will be abandoned?
- Because this always happen. We are dissatisfied with some properties of Schrödinger Eq. Scientist are ready to change. Believers are not.

---

### Quantum computing
- Relevant [unitary](https://en.wikipedia.org/wiki/Unitary_matrix) transformation of state qubits. Reversible transitions.
- We search some Hamiltonian to implement desired transition $\Psi(0) \rightarrow QC(U)\rightarrow \Psi(1)$
- Solving **reverse** problem. Construct a Hamiltonial for a desired logical operations.
- in QM any observable has a corresponing operator.

---

## Lecture 2.
**Plan**
- Calculations
- Superposition and entanglement
- parallelism
- Copying of qubits
- $\sqrt{NOT}$
- quantum Zeno's paradox

---

### Computations
- States should correspond to definite values of [observable](https://en.wikipedia.org/wiki/Observable) (e.g. enegry level, magentisation)
- This allows direct interpretation of superposition parameters.
$\psi = c_1|\psi_1\rangle+c_2|\psi_2\rangle$, where $|c_1|^2+|c_2|^2=1$, where $|c_i|^2$ represents probability to observe state $|\psi_i\rangle$.
- with single experiment we cannot restore the the parameters.
- if we change a basis, for a clean state we will get superposition of the other basis.

---

### Superposition
Independent superposition of 2 states:
$|\psi_1\rangle=\frac{1}{2}(|00\rangle+|01\rangle+|10\rangle+|11\rangle) =
\frac{1}{2}(|0\rangle+|1\rangle)(|0\rangle+|1\rangle)$

Can be represented as a multiplication.

But there are other examples:
$|\psi_2\rangle=\frac{1}{\sqrt{2}}(|00\rangle\pm|11\rangle)$

They cannot be represented as a product!

$|\psi_3\rangle=\frac{1}{\sqrt{2}}(|01\rangle\pm|10\rangle)$

If state cannot be represented as a product of independent state, these states are called [entangled](https://en.wikipedia.org/wiki/Quantum_entanglement).

*Opinion*: we should think about something like a "memory" of a quantum system. Qubits could not be in entangled without interacting in the past.

---

### Quantum parallelism
- ability to evaluate a function for all "tapes" of Turing machine.
$\frac{1}{\sqrt{2}}(|0\rangle\pm|1\rangle)$
apply some operation
$y+f(x)\mod 2$
For many states at one time:
$\Psi=\frac{1}{\sqrt{2}}(|0,f(0)\rangle+|1,f(1)\rangle) \rightarrow ... \rightarrow \frac{1}{\sqrt{2^N}} \Sigma |x\rangle f(x)$

---

### CNOT
In classical computer CNOT makes a copy of a state. For a superposition in created an entangled state!

$\Psi_1=a|0\rangle+b|1\rangle \rightarrow ... \rightarrow a|00\rangle + b|11\rangle$

---

### Square root of NOT

$\sqrt{NOT} = \begin{pmatrix} (1+i)/2 & (1-i)/2 \\
(1-i)/2 & (1+i)/2 \\ \end{pmatrix}$

$\sqrt{NOT}\sqrt{NOT}=NOT$

Is actially existing operation, which corresponds to an exact action, and the result can be obtained through another calculation basis.

---

### Teleportation
To [teleport](https://qiskit.org/textbook/ch-algorithms/teleportation.html) a qubit STATE:
1. Alice creates a pair of entangled qubits B, C.
2. Entangles with A.
3. Measures the state of one of BC
4. Calls Bob and informs about the state.
5. Bob now knows what to do to proper transformation.

!! Spin depends to creation of molecules. Trees while converting light into molecules create $\frac{1}{\sqrt{2}}(|01\rangle-|10\rangle)$ entangled states in a wild.

---

### Quantum Zeno's paradox
To make sure everything is ok, we should control and measure (error correction). But is we measure to often, system slows down. If we control too much, QC will stop!

---

## Lecture 3. Postulates of Quantum Mechanics

Ideas (recap):
- information does not exist without physical implementation.
- In QC we should use completely different logic.
- In quantum computing $\sqrt{NOT}$ can be measured in experiment!

Agenda:
- basics of Quantum Mechanics.

---

Description on objects in Classic Mechanics is just coordinated and impulse. Far from being full.

---

### Classical mechanics description
- there is radius vector $r$ and momentum $p$
- Solutions can predict fully the state.


---

### What is light?

Waves or particles? Both.
Why light is a particle? [Double-slit experiment](https://en.wikipedia.org/wiki/Double-slit_experiment).

Today we can observe a very small part of light. If we do this with a singe particle, then one quanta of light creates a signal in a single location. No interference effect. Thus it behaves as a particle.

---

[De Broglie](https://en.wikipedia.org/wiki/Louis_de_Broglie) - particles should show properties of waves and mass should be connected to wave freq. See [this page](https://en.wikiversity.org/wiki/De_Broglie_wavelength).
$\lambda=h/p=h/(mv)=10^{-31} cm$
if $m=1g$ then $v=10^5cm/s$, but if $m=100kg$, then $\lambda=10^{-36}cm$, that is why we don't feel ourselves as waves :)

[Schrodinger classic work "Quantisierung als Eigenwertproblem"](http://www.fisicafundamental.net/relicario/doc/Schrodinger1926a.pdf)

---

### Postulates of QM. Postulate 1
**State of a particle is given by a wave function $\psi(r,t)$ (not position and impulse!). Function can be called a "vector of space" (not a typical vector we used to) if it follows some properties.**
- Wave Function is not observable. Misterious. But any observable should be quadratic functional of WF.
- $|\psi(r)|^2$ -- is a probabilit to find a particle in $r$ in a single experiment.
!! $r$ is radius-vector and $t$ is time. But sometimes there can be time/coordinate-independents functions, thus we sometimes omit.

---

- Principle of superposition: $\psi=c_1\psi_1+c_2\psi_2$. This property is known for the waves in classical mechanics, but now we define it for any particle too! In classic superposition in we can observe "something average", but in quantum case we will observe one of 2 states only.

---

- Wave functions can be defined not only in $r$ (coordinate) space. This can be some other, e.g. $p$ (momentum) of spin.
- 2 non-interacting particles can be separated to a multiplication:
$\psi(1,2)=\psi(1)\psi'(2)$
$|\psi(1,2)\rangle=\frac{1}{2}(|0_10_2\rangle+|0_11_2\rangle+|1_10_2\rangle+|1_11_2\rangle) =
\frac{1}{2}(|0_1\rangle+|1_1\rangle)(|0_2\rangle+|1_2\rangle)$
Subscripts mean that qubits live not in the **same** space, but in **similar** spaces.
Also, measurement will give one of allowed states! E.g. if observable is energy, observable will be one of $E_1+E_1, E_1+E_2, E_2+E_1, E_2+E_2$.

*Q*: How we distinguish $E_1+E_2, E_2+E_1$?
*A*: We observe a superposition $\frac{1}{\sqrt{2}}(|01\rangle+|10\rangle)$. Thus we need to run additional experients to collapse. But if we choose different energy levels for different qubits, then we can determine.

---

- For an interacting particles you cannot represent common wave function as a product. Interaction can be at moment of observation, or any moment at the past. E.g. $|\psi(t)\rangle = c_1(t)|10\rangle-c_2(t)|01\rangle$. This state is called [Einstein–Podolsky–Rosen pair](https://en.wikipedia.org/wiki/EPR_paradox).

---

**Alternative description of a state**
Wave function is determned for for very close systems. We cannot consider models in thermodinamic equilibrium

**[Density matrix](https://en.wikipedia.org/wiki/Density_matrix)**
In a superposition $c_0\psi_0+c_1\psi_1+...$ coefficient correspond to "contribution". If we build a matrix $2^N\times2^N$ of coefficients $c_0^*c_0$, $c_0^*c_1$, ..., $c_1^*c_0$, .... Where $N$ is the number of qubits.

$\begin{pmatrix}
c_0^*c_0 & c_0c_1 & ... & c_0^*c_{2^N} \\
c_1^*c_0 & c_1^*c_1 & ... & c_1^*c_{2^N} \\
... & ... & ... & ... \\
c_{2^N}^*c_0 & c_{2^N}^*c_1 & ... & c_{2^N}^*c_{2^N}
\end{pmatrix}$

- diagonal elements $c_i^*c_i=|c_i|^2$ are probabilities to observe in some state.
- non-diagonal characterize quantum coherence. If coherence go goes to $0$ quantum computers just becomes classic.
- If we collapse wave function the matrix will be all zeros except single $1$ on a diagonal.

Opinion: we can include different time-dependent relaxation (e.g. interaction with thermostat).


---

### Postulate 2

**Observables of Classic Mechanics are represented by [Hermitian operators](https://en.wikipedia.org/wiki/Hermitian_adjoint#Hermitian_operators)**
$H^*=H$

Example:
Coordinate and it's operator
$x\rightarrow x$

Impulse and it's operator in classical form
$p_x=-i\hbar\frac{\partial}{\partial x}$

Energy operator ([Hamiltonian](https://en.wikipedia.org/wiki/Hamiltonian_(quantum_mechanics))) -- here we consider only kinetic energy:

$E_k=\frac{1}{2}mv^2=\frac{1}{2}pv=\frac{p^2}{2m}$

$H= \frac{p_x^2}{2m} \rightarrow -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}$

Properties of:
- there are actions which does nothing with a state of the system (see eigenvectors and eigenvalues). Eigenfunction. $\hat{H}\psi_n=E_n \psi_n$.
- Eigenvalues of Hermitian operators are all real numbers. Otherwise observables would become complex, which is physically strange.
- Not required, but usually we use eigenfunctions to present a spin.


[Pauli matrices](https://en.wikipedia.org/wiki/Pauli_matrices)

Electron spins (these are state, not numbers!)
$\alpha=|+\frac{1}{2}\rangle$
$\beta=|-\frac{1}{2}\rangle$

$S_x$ -- observable (spin projection to x), which should be from $\{-\frac{1}{2}, \frac{1}{2}\}$.
Thus, applying operator of a spin:

$S_x|-\frac{1}{2}\rangle=S_x\begin{pmatrix}0\\1\end{pmatrix}$

See [quadratic form](https://en.wikipedia.org/wiki/Quadratic_form#Real_quadratic_forms)

$\langle-\frac{1}{2}|S_x|-\frac{1}{2}\rangle=\begin{pmatrix}0 & 1 \end{pmatrix} \begin{pmatrix}1/2 & 0 \\ 0 & -1/2 \end{pmatrix} \begin{pmatrix}0 \\ 1 \end{pmatrix}$

### Square root of NOT

If we apply not, then we just transfer from one state to another.
Square root creates a superposition.

$\sqrt{NOT} = \begin{pmatrix} (1+i)/2 & (1-i)/2 \\
(1-i)/2 & (1+i)/2 \\ \end{pmatrix} = \frac{1}{2(1-i)} \begin{pmatrix} (1+i)(1-i) & (1-i)(1-i) \\
(1-i)(1-i) & (1+i)(1-i) \\ \end{pmatrix}$

$= \frac{1}{2(1-i)}\begin{pmatrix} 1+i^2 & 1+i^2-2i\\
1+i^2-2i & 1+i^2 \\ \end{pmatrix} = \frac{1}{2(1-i)}\begin{pmatrix} 0 & -2i\\
-2i & 0 \\ \end{pmatrix} = -\frac{i}{1-i}S_x$

From eigenstate of one observable $S_z$ we go to eigenstate of another observable $S_x$.

---

## Lecture 3.

Start from refresher of Postulate 1.

$\psi=a\psi_1+b\psi_2$ can be expressed in matrix form

$\rho=\begin{pmatrix}|a|^2 & a^*b \\ ab^* & |b|^2\end{pmatrix}$

$\rho_{kn} = \langle\psi_k|\rho|\psi_n\rangle, n=1,2$

Any matrix elements of density matrix can be observed, they are all observables.

Any observable is has an operator, this operator has to be Hermitian (H transposed and complex conjugate = H)

Eigenvalues can be measured in experiment.

**Postulate 2**
**Observables of classic mechanics are Hermitian operators**

---

### Posutulate 3.
**Every observable in quantum mechanics is represented by an operator which is used to obtain physical information about the observable from the state function. For an observable that is represented in classical physics by a function $Q(x,p)$, the corresponding operator is $Q(\hat{x},\hat{p})$**
[<ref>](https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Quantum_Mechanics/04._The_7_Postulates_of_Quantum_Mechanics/Postulate_3%3A_Quantum_Mechanics)

$\hat{H}\psi(r,t)=i\hbar\frac{\partial\psi}{\partial t}$

In isolated system $H$ does not change in time.

$\psi(t)=e^{-iHt/\hbar}\psi(0)$

$H$ - operator of energy, kinetic (of impulse $p_x$) + potential (of position in a field $x$)

$E=\frac{p_x^2}{2m}+V(x)=-\frac{\hbar^2\partial^2}{2m \partial x^2} + V(x)$

---

If we are in one of eigenstate, with probability $1$ we will measure eigen-energy $E_n$.

$H\psi_n=E_n\psi_n$

In superposition we will obtain $E_n$ with probability
$p_n=|\langle\psi|\psi_n\rangle|^2$

$\langle\psi|\psi_n\rangle=\int dv \psi^*\psi_n$

!!$\langle a|b\rangle$ -- [bra-ket notation](https://en.wikipedia.org/wiki/Bra%E2%80%93ket_notation) means the scalar product.

This can be understood as a projection of one vector $a$ (state) onto another $b$ (e.g. base vector).

---

### Creation of [pure state](https://en.wikipedia.org/wiki/Quantum_state#Pure_states)

*pure quantum states correspond to vectors in a Hilbert space, while each observable quantity (such as the energy or momentum of a particle) is associated with a mathematical operator.*

We believe we can run an experiment without dsiturbing the system (in classic). In Quantum -- differerent.

Suppose we have a partice in superposition.
$\psi=\sum_n c_n \psi_n$

Suppose $\psi_n$ are eigenvectors of Hamiltonian $H$.

When we measure energy of thea particle, we will obtain only ONE, $k$-th of the eigenvalues of H $E=E_k$, and wave function will [**collapse**](https://en.wikipedia.org/wiki/Wave_function_collapse) to $\psi_n$.

---

### Desription of state ensemble

Suppose qubits never interacted.

$\psi_1=a_1|0_1\rangle + b_1|1_1\rangle$ -- particle 1
$\psi_2=a_2|0_2\rangle + b_2|1_2\rangle$ -- particle 2

Together they are

$\psi=\psi_1 \psi_2=a_1 a_2|0_10_2\rangle+a_1b_2|0_11_2\rangle+b_1 a_2|1_10_2\rangle+b_1b_2|0_11_2\rangle$

$CNOT\psi=a_1 a_2|0_10_2\rangle+a_1b_2|0_11_2\rangle+b_1 a_2|1_11_2\rangle+b_1b_2|0_10_2\rangle$

Now we cannot represent this as a product of $\psi'_1\psi'_2$.

---

Now we want to learn in which state is the first qubit?

Solution can be done using density matrix.
$|1\rangle=|00\rangle, |2\rangle=|01\rangle, |3\rangle=|10\rangle, |4\rangle=|11\rangle$

$\psi=a_1|1\rangle+a_2|2\rangle+a_3|3\rangle+a_4|4\rangle$

in matrix form:
$\rho=\begin{pmatrix}
|a_1|^2 & a_1^*a_2 & a_1^*a_3 & a_1^*a_4 \\
a_2^*a_1 & |a_2|^2 & a_2^*a_3 & a_2^*a_4 \\
a_3^*a_1& a_3^*a_2 & |a_3|^2 & a_3^*a_4\\
a_4^*a_1& a_4^*a_2 & a_4^*a_3 & |a_4|^2 \\
\end{pmatrix}$

---

Summing the 2 terms give the probability irrespective to the other qubit. $\sigma(1)=Tr_2 \rho(1,2)$ and $\sigma(2)=Tr_1 \rho(1,2)$

$\sigma_{00}=\rho_{11}+\rho_{22}$

Non-diagonal elements: $\sigma_{01}=\rho_{13}+\rho_{24}$

Transition from AB system ($\rho$) to A ($\sigma$) we **loose information about quantum coherence** (0-, and 2-quantum coherence).

$\rho$ express transition.
Term $\rho_{14}$ two-quantum coherence: both qubits become excited.
Term $\rho_{23}$ zero-quantum coherence: one looses energy, another obtains.

---

In the unusual world strange properties are declared. But then these properties are supported. The paradigm shift. New generations challenge it, but the idea survive. [ref](https://www.nature.com/articles/s41598-021-90668-8)

---

### Two-state systems

Circularly polarized photons, topological isolators, superconductive units can serve as qubits.

Electron spins $\pm\frac{1}{2}$ as qubits in atoms with one unpaired electron: $H, Li, Na, K, ...$. Also organic free radicals $CH_3-, CH_3-CH_2$. Also nuclear spin $I=\pm\frac{1}{2}$

In Russia photon is considered the most promising candidates.

In principle, hidrogen has two 2-level systems: electon and nuclear spin.

---

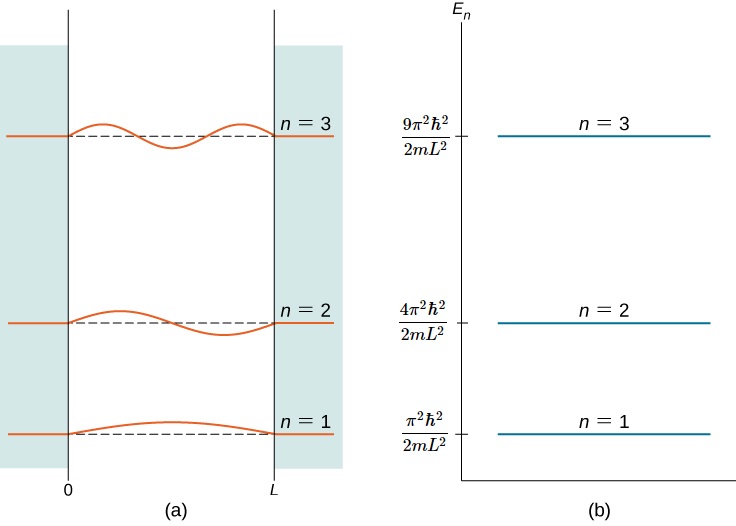
### Electron in 2 potential boxes

$E_n=\frac{\pi^2\hbar^2}{2ma}n^2$

$\psi_n=\sqrt{\frac{2}{a}}\sin(\frac{\pi b}{a}x)$

![](https://chem.libretexts.org/@api/deki/files/125866/CNX_UPhysics_40_04_boxstates.jpg?revision=1&size=bestfit&width=599&height=428
)

---

Along with mass and charge electron has inherent angular moment, called spin.

Magnetic moment $\mu=-2\mu_B S$
See [Bohr magneton](https://en.wikipedia.org/wiki/Bohr_magneton).

$H=-\mu B$ -- scalar product of moment in external magnetic field.

Suppose $OZ || B$, Then $B=(0, 0, B)^T$

Thus, $H= -2 \mu_B B S$

From experiments we know $S_z$ has 2 values $m=\pm\frac{1}{2}$

---

Q: why half?
A: we have 2 values. In classic mechanics spin appears as an additive to normal angular moment (from motion in space). BUT normal orbital magnetic moment ... $1s$ in hidrogen has 0 moment. angular momentum $\overrightarrow{L}=\overrightarrow{r}\times \overrightarrow{p}$. There are $2L+1$ projections: $-L, -L+1, ...0, ..., L$. There is also a spin with 2 projections. It has the same properties as momentum. We want them to be $-s, -s+1, ..+s$. We want the difference to be 1, and there is no $0$.

---

All 2-level systems create isomorphic groups. Any discoveries for one 2-level system can be used for the others. We can "define" a "spin" for any other system, thus we can proceed with spin as general approach.

---

Let's suggest we have a system with 2 projections.

$S_z|m\rangle = m |m\rangle$

$|-1/2\rangle=|0\rangle, |+1/2\rangle=|1\rangle$

$S_z=\begin{pmatrix}-1/2 & 0 \\ 0 & 1/2\end{pmatrix}$
$S_x=\begin{pmatrix} 0 & 1/2 \\ 1/2 & 0\end{pmatrix}$, $B=(B, 0, 0)^T$


This is an evolition operator:

$\psi(t)=e^{-iHt/\hbar}\psi(0)$.

If we consider $H=\hbar\omega S_z$, so we need to find **evolution operator**. It can be reduces to a very simple formula:

$L=e^{-i\omega t S_z} = ... = cos(\omega t/2)U-i2sin(\omega t/2)S_z$

!! $U=I$ -- identity operator.
!! $e^{ix}=1-ix-\frac{x^2}{2!}+...$

$e^{-i\omega t S_z}(a|0\rangle + b|1\rangle)=ae^{i\omega t /2}|0\rangle + be^{-i\omega t /2}|1\rangle$

Evolution operator acts on $|0\rangle$. This eigenfunction of Hamiltonian. Eigenvalue is $-1/2$, thus we have first term. The same for the second term. Probability to observe doesn't change (absolute values of exponent are 1), but we have phase change, coherence change, non-diagonal elements change.

When we apply magnetic field along X-axis.

$e^{-i\omega t S_x}=cos(\omega t/2)U - i2sin(\omega t/2)S_x$
$e^{-i\omega t S_x}|0\rangle=\cos(\omega t/2)|0\rangle - i \sin(\omega t/2)|1\rangle$

$e^{-i\omega t S_x}|1\rangle=\cos(\omega t/2)|1\rangle - i \sin(\omega t/2)|0\rangle$

When $\omega t=\pi$, then $e^{-i\pi S_x}$ gives the operator $NOT$.

When $\omega t=\pi/2$, then $e^{-i(\pi/2)S_x}$ gives the operator $\sqrt{NOT}$.

Just applying constant magnetic field during definite time, we can convert 0 to 1 and vice versa.

---

### Math description of 2-state system

We have to know, which property we use to differentiate the states.
1. We choose observable to measure. E.g. $H\psi_n=E_n\psi$
2. The set of eignestates $\{\psi_n\}$ we chose basis states $\langle \psi_n | \psi_k \rangle=\delta_{nk}$ -- delta-function $n == k \rightarrow 1$
3. $\psi=\sum c_n\psi_n$, $c_n=\langle \psi_n | \psi \rangle$
4. For qubits. We have 3 independent parameters for a qubit.
- either $c_1=|c_1|e^{-i\phi}, c_2=|c_2|e^{-i\theta}, |c_1|^2+|c_2|^2=1$
- or density matrix (4 elements, but with constraints): $\sigma_{21}=\sigma_{12}^*$ and $\sigma_{11}+\sigma_{22}=1$

Thus we can express any 2-state system with 3 independent parameters, one of which can be $n=\sigma_{11}-\sigma_{22}$ -- population difference of states 1 and 2.

---

1. All observables are presented as 2x2 Hermitians

2. Any Unitary operator Q can be represented in a unique way $Q=q_0I+q_x\sigma_x+q_y\sigma_y+q_z\sigma_z$ in a basis of Identity matrix + [Pauli matrices](https://en.wikipedia.org/wiki/Pauli_matrices).

3. When spin s=1/2 is chosen as qubit, then $\sigma_z=2S_z$
$H=2\mu_B(SB)$. Support $OZ||B$, then $B=(0, 0, B)^T$, $H=2\mu_B BS_z$

---

We can use $S_i$ instead of $\sigma_i$ as they coinside with coefficient 1/2.

---

## Lecture 4. Using $e^-$ spins to implement logic operations

1. Any 2-level quantum system can solve as a qubit, physically they might be different, evolutions are done diferently, but mathematically they are similar (equivalent isomorphic).

2. We have naturally 2-level systems -- particles with spin $\frac{1}{2}$.

---

To build a quantum computer this is enough to have $NOT$ and $CNOT$.

Evolution of a system can be interpreted as realization of certain logic operations.

$\psi(t) = c_o(t)|0\rangle+c_1(t)|1\rangle$

$\psi(t) = e^{iHt/\hbar}\psi(0)$. -- at one moment $t_0$ we can observe (during evolution) $|c_1(t_0)|^2 = 1$, which can be considered as $NOT|0\rangle$. This creates opportunities as well as problems.

---

There are no "ready" qubits in nature. There are no constant Hamiltonians. We search for dynamic implementations.

- required 1-qubit operations: $NOT$, Hadamard $H$, Phase shift
- required 2-qubit: $CNOT$

---

If relaxation is fast, we cannot state "we implemented NOT". To serve as qubit values, relaxation shouls be $10^{3-4}$ times longer, then the process of operation itself.

---

One qubit logic operators.

$\sigma_x$ is exactly $NOT$ implementation.

$NOT = \sigma_x=\begin{pmatrix}0 & 1 \\ 1 & 0\end{pmatrix}$

Problem is to find a corresponding Hamiltonian.

---

### Representing Hamiltonian in matrix basis

Matrix can be represented in a basis of $I$ and Pauli matrices.

$H=c_0I+\sum_{i=x,y,z}c_i\sigma_i=c_0I+2\sum_{i=x,y,z}c_iS_i$

$H=c_oI+2\epsilon(nS)$

$nS=\frac{1}{\epsilon}\sum_{i=x,y,z}c_iS_i$

$\epsilon=\sqrt{(|c_x|^2+|c_y|^2+|c_z|^2)}$

---

### Simplification

Exponential operator can be reduces to a very nice form due to $e^{-i\phi}=\cos\phi-i\sin\phi$ followed by:

$e^{-i\phi S_z}=cos(\phi/2)*I-i2S_z \sin(\phi/2)$

Thus we can rewrite:

$L=e^{-iHt/\hbar}=e^{2i\epsilon t/\hbar}=cos(\frac{\epsilon t}{2})*I-2i\sin(\frac{\epsilon t}{2})*(nS)$

---

### What if we apply magnetic field with one projection

If we only have $S_x$ (magnetic field $\perp$ to quantization axis $Z$):

$B=\{B, 0, 0\}$

$H=2\mu_BBS_x$

[Rabi frequency](https://en.wikipedia.org/wiki/Rabi_frequency)

$\omega=2\frac{\mu_B B}{\hbar}$

$H=\hbar\omega S_x$

---

### How to catch the moment to build NOT gate

if $\epsilon t=\pi$, then **for this particular time**:

$L_{\pi}=e^{-i\pi S_x}=-2S_x=-NOT$

$L_{\pi}(a|0\rangle+b|1\rangle)=(-1)(b|0\rangle+a|1\rangle)$

in magnetic field ~1 [Guass](https://en.wikipedia.org/wiki/Gauss_(unit)) for electron this time is ~$10ns$ with relaxation of microseconds. Inside fullerene relaxation time is up to milliseconds, for the nuclear spin relaxation time is hours, but operator may take milliseconds (can work for demo only).

---

### Square root of $NOT$

If time is twice as small $\epsilon t = \pi/2$:

$L_{\pi/2}=-i2Sx=(1+i)\sqrt{(NOT)}$ -- ideal operator to produce random numbers, since
$\sqrt{NOT}|0\rangle=\frac{1}{\sqrt{2}}(|0\rangle+i|1\rangle)$

---

### Hadamard

$B=\{B, 0, B\}$ -- external field has both components. Vector precese around middle position.

$H=\omega (S_x+S_z)$

$L_{\omega t}=
\sqrt{\pi/2}=e^{-i\omega t (S_x+S_z)}=$
$=\frac{i}{\sqrt{2}}\begin{pmatrix}sin(\frac{\omega t}{\sqrt{2}}) & -sin(\frac{\omega t}{\sqrt{2}}) \\ -sin(\frac{\omega t}{\sqrt{2}}) & (-i)cos(\frac{\omega t}{\sqrt{2}})-sin(\frac{\omega t}{\sqrt{2}})\end{pmatrix}$

$L=-iH=-i*\frac{1}{\sqrt{2}}\begin{pmatrix}1 & 1 \\ 1 & -1\end{pmatrix}$ where $H$ stands for [Hadamard operator](https://en.wikipedia.org/wiki/Quantum_logic_gate#Hadamard_gate).

---

### CNOT

$CNOT=\begin{pmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&0&1\\ 0&0&1&0\\ \end{pmatrix}$

$CNOT(
c_0|00\rangle+
c_1|01\rangle+
c_2|10\rangle+
c_3|11\rangle
)=$
$=
c_0|00\rangle+
c_1|01\rangle+
c_3|10\rangle+
c_2|11\rangle$

---

### No independent implementation
It is evident, we cannot implement $CNOT$ without considering interation of two qubits.

if

$H=H_1+H_2$

then
$L=e^{-iHt/\hbar}=L_1*L_2$
$\psi=\psi_1\psi_2$ since $[H_1,H_2]$ (they [commutate](https://en.wikipedia.org/wiki/Commutator))

---

### Impementation (result)

We will look in a form of stroboscopic form (time dependent, as we did for $NOT$)

$H=\omega s S_z + \omega f F_z + K S_z F_z$

by [[J. A. Jones, M. Mosca, 1998]](https://www.semanticscholar.org/paper/Implementation-of-a-quantum-algorithm-on-a-nuclear-Jones-Mosca/773cb967b3d6f1e10d60577cbb45ff80484cfa93) for nuclear spins

and

$H=\omega a S_z + \omega b F_z + A S_z F_z+B(S_x F_x+S_y F_y)$

by [[Volkov, Salikhov, 2011]](https://link.springer.com/article/10.1007/s00723-011-0297-2) for electron spins

---

### whiteboard
Let $\hbar = 1$
$H=\omega_s S_z + \omega_z F_z+jS_zF_z$

$L=e^{-iHt}$

$F_z,S_z|0\rangle=\frac{1}{2}|0\rangle$
$F_z,S_z|00\rangle=\frac{1}{4}|00\rangle$

We should force spins with this Hamiltonian interfere using pulses of magnetic field.

---


Formula explanation:
We insert $L^{-1}L= I$ - 2 pulses rotating in opposite direction. Thus we obtain in the formula $LHL^{-1}=\hat{H}$ twice in a row ($\hat{H}^2$), which can be considered as free evolution under new Hamiltonian (we "edited" Hamiltonian).

---

Q&A: electrons should not be closer then $1nm$, but not too far (magnetic fields should overlap to some extent). E.g., in $H_2$ (hydrogen) 2 electrons with opposite spins are too close, that they are magnetically neutral and impossible to manipulate with magnetic impulses.

---

Simplest basis to represent matrix is 4x4 matrix with only 1 non-zero elements. There will be 16 of them.

Notation for solution:

$I=U_0$

$I_x=\begin{pmatrix}
0 & 1/2 & 0 & 0 \\
1/2 & 0 & 0 & 0 \\
0 & 0 & 0 & 1/2 \\
0 & 0 & 1/2 & 0 \\
\end{pmatrix}$

$S_z=\begin{pmatrix}
1/2 & 0 & 0 & 0\\
0 & 1/2 & 0 & 0 \\
0 & 0 & -1/2 & 0 \\
0 & 0 & 0 & -1/2 \\
\end{pmatrix}$

Thus we can construct:
$E_{1+}=I/2+S_z=\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
\end{pmatrix}$

$E_{1-}=I/2-S_z=\begin{pmatrix}
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}$

They are interesting. Squares are equal to itself. And they are orthogonal (we use it later).

If we are in the first subspace $E_{1+}$ -- nothing happens. Otherwise in $E_{1-}$ subspace $NOT = \alpha I_x$ flip happens: ($2I_xE_{1-}$)

$CNOT=E_{1+}+2I_xE_{1-}=$

$=E_{1+}E_{1+}+2I_x E_{1-}E_{1-}=$

added 0

$=E_{1+}E_{1+}+2I_x E_{1-}E_{1-} + iE_{1+}E_{1-}=$

added one more 0

$=E_{1+}E_{1+}+(-i^2)2I_x E_{1-}E_{1-} + iE_{1+}E_{1-} - 2iI_xE_{1+}E_{1-}=$

$=E_{1+}(E_{1+} + iE_{1-}) - i2I_xE_{1-}(E_{1+} + iE_{1-})=$
$=(E_{1+} - i2I_xE_{1-})(E_{1+} + iE_{1-})$ (+)

knowing that:

$e^{GE_{1+}}=I+GE_{1+}+\frac{1}{2!}G^2E_{1+}+\frac{1}{3!}G^3E_{1+}$

add 0:

$e^{GE_{1+}}=I +(E_{1+}-E_{1-}) + GE_{1+}+\frac{1}{2!}G^2E_{1+}+\frac{1}{3!}G^3E_{1+}+...=$

$=E_{1+}(1+G+\frac{G^2}{2}+...)=E_{1+}e^G$

and

$i=e^{i\pi/2}$

Then (+) becomes

$=(e^{-2I_xE_{1-}})(e^{i\frac{\pi}{2}E_{1-}})$

**This is a product of 2 exponents**. This is a form of solution of Schrödinger equation.

---

How to make our Hamiltonial $Le^{-\alpha S_zI_z}L^{-1}$ to function as $I_xS_z$?

we can rotate a spin $90^{0}$ around $Y$.

$e^{i\pi/2y}e^{-\alpha S_zI_z}e^{-i\pi/2y}$.

---

Note: System will work as quantum computer, if the [fidelity](https://en.wikipedia.org/wiki/Fidelity_of_quantum_states) is more then 80%.

---

## Lecture 5. QFT, quantum teleportation, and Quantum Zeno's paradox

Notes:
- systems evolve without control, as they are implemented as physical objects.
- superposition is rather trivial. But observables interesting things. We will not see superposed values, but only 2 allowed states.
- But if we do multiple experiments -- we (using [Ergodic hypothesis](https://en.wikipedia.org/wiki/Ergodic_hypothesis)) can observe how values converge to.
- when we speak about $|0\rangle$ and $|1\rangle$ -- they are not abstract. They are eigenstates of some observable.
- when we use different observables, they have different bases. We usially take spin projection, but we can take [Zeeman effect](https://en.wikipedia.org/wiki/Zeeman_effect) $H=-\vec{\mu}\vec{B}$.
- Any operator space and be represented using set of $2\times2$ matrices - Identity and Pauli matrices.
- in fluctuating systems, if vector [precesses](https://en.wikipedia.org/wiki/Precession) (rotates) around axis, we can use Rabi frequency to understand, **when** e.g. $NOT$ occures. Thus, we manipulate with short pulses.
- Errors occur when we are not exact in pulse lengthes. Longer the sequence of pulses, bigger is the accumulated error.
- In classic systems we assume measurements does not distub the system. Error correction -- if wrong, then flip. Measurement in Q systems is different. Thus, error correction is more complicated.
- Any program can be reduced to a set 1- or 2-qubit operations.
- Quantum probabilisting vs classic: each time we perform operation, classic computer performs an operation and "reduces" the state. In quantum systems until reduction we evolve by all possible trajectories.

---

### [Quantum Fourier Transform](https://en.wikipedia.org/wiki/Quantum_Fourier_transform)

Some vector in the basis:
$Y_k=\frac{1}{\sqrt{2^N}}\sum_m X_m e^{\frac{i2\pi mk}{2^n}}$
m - means time dependence
k - which state we have.

Thus, Fourier transform -- is an operator.

$UQFT=\frac{1}{\sqrt{2^N}}\sum_{m=0}^{n-1}\sum_{k=0}^{n-1}e^{\frac{i2\pi mk}{2^n}}|k\rangle\langle m|$

$|m\rangle=\frac{1}{\sqrt{2^N}}\sum_m e^{\frac{i2\pi mk}{2^n}} |k\rangle$

for n = 1 this is just Hadamard gate :)

for n=2 we have the following:

$|m\rangle = \frac{1}{2}(|0\rangle+e^{i\pi m}|1\rangle)(|0\rangle+e^{i\pi m /2}|1\rangle)$

**SHOW THIS IS TRUE -- possible exam question**

$(|0\rangle + e^{i\phi}|1\rangle$) is already familiar - Hadamard + phase shift.

---

### Quantum teleportation

Suggested in 1993. Teleportation: take and object, describe it fully, send information and then restore.

QT -- the state of one qubit we reproduce in another state. The state of original qubit is lost.

Alice wants to send a qubit state to Bob. Alice has a qubit with **unknown** state (if known - this means she measured it!). Alice also prepares a pair of highly entangled state ([Bell state](https://en.wikipedia.org/wiki/Bell_state)) $|\psi_{BC}\rangle=\frac{1}{\sqrt{2}}(|01\rangle-|10\rangle)$ -- [singlet state](https://en.wikipedia.org/wiki/Singlet_state).

$|\psi_{BC}\rangle\neq|\psi_{B}\rangle|\psi_{C}\rangle$

After this pair is shared between Alice and Bob.

Let us consider aggregate state of the system.

$|\psi_{ABC}\rangle=\frac{1}{2}(a|0\rangle + b|1\rangle)(|01\rangle-|10\rangle)=\frac{1}{2}(a|001\rangle-a|010\rangle+b|101\rangle-b|110\rangle)$.

Total wave function in the basis of Bell states:

$|\psi_{ABC}\rangle=
|\psi_{A}\rangle| \psi_{BC}\rangle=
c_1|\psi_{A} s\rangle
+c_2|\psi_{A} T_1\rangle
+c_3|\psi_{A} T_{-1}\rangle
+c_4|\psi_{A}T_0 \rangle$.

Alice wants to know in which states are her qubits? She measures in a basis of Bell states. $T$ stands for [Triplet states](https://en.wikipedia.org/wiki/Triplet_state).

For example, multiply by $(|0_A1_B\rangle-|1_A0_B\rangle)$. Why? We want to measure (project) AB onto a single Bell state (for clarification read below). This is not the same as two measurements! And we get:

$\langle\psi_{AB}|\psi_{ABC}\rangle
=-\frac{1}{\sqrt{2}}
(a|0\rangle + b|1\rangle )$

$-a|0_C\rangle-b|1_C\rangle=e^{i\pi}(a|0_C\rangle+b|1_C\rangle)$.

Wow! Qubit C is in a superposition with the coefficient of A. If we multiply with other Bell states, we get either swapped a,b or sign changed. This can be easily fixes with $X$ and $Z$ gates if Bob knows exact observed state of Alice's pair.

Alice calls Bob and tells information is in a definite state (2 bits).

*!! Sound like we are missing A and B qubits entanglement?* **[For details look here](https://qiskit.org/textbook/ch-algorithms/teleportation.html)**

This thing is tricky. The protocol doesn't specify **how to measure a pair of qubits in the basis of Bell states**. In other implementation to avoid this operation, A and B are entangled, thus we can be SURE that measured A and B states does not depend on this unknows operation, we can do the same with regular measurements.

---

### Quantum Zeno's paradox

Consequence of quantum objects participating in computations. Measurement of qubits leads to decoherence. Decoherence affects the qubit dynamics. Frequent control (e.g. in error correction) reduces the rate of quantum computations.

$|0\rangle$. Start with state. Apply magnetic field. Magnetic moment will rotate (from the pole). Now $a|0\rangle+b|1\rangle$. The whole process of continued transition with $prob(t)=|b|^2$ form an oscillating function of probability of $NOT$. If at some time we check that there is "ok", we immediatly transfer the system to one of the states. Thus we "steal" some time from computations. The more frequently we check, the slower is the operator.

---