###### tags: `leetcode` `medium` `Array` `Dynamic Programming` `Matrix`
# [931. Minimum Falling Path Sum](https://leetcode.com/problems/minimum-falling-path-sum/description/)

## Description

Given an `n x n` array of integers `matrix`, return *the **minimum sum** of any **falling path** through* `matrix`.

A **falling path** starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position` (row, col)` will be `(row + 1, col - 1)`,` (row + 1, col)`, or` (row + 1, col + 1)`.

## Examples
### Example 1:

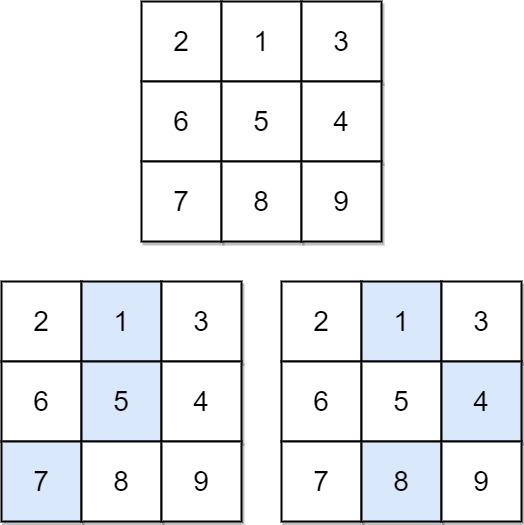
**Input**: matrix =` [[2,1,3],[6,5,4],[7,8,9]]`
**Output**: 13
**Explanation**: There are two falling paths with a minimum sum as shown.

### Example 2:

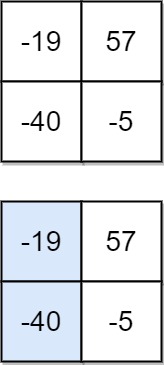
**Input**: matrix =` [[-19,57],[-40,-5]]`
**Output**: -59
**Explanation**: The falling path with a minimum sum is shown.

## Constraints:

- $n == matrix.length == matrix[i].length$
- $1 \leq n \leq 100$
- $-100 \leq matrix[i][j] \leq 100$

## Code

int minFallingPathSum(int** matrix, int matrixSize, int* matrixColSize){
    int **localMin = (int**)malloc(matrixSize * sizeof(int*));
    int left, mid, right, min, row, col;
    for(int i = 0 ; i < matrixSize ; i++)
        localMin[i] = (int*)malloc(sizeof(int) * matrixSize);
    for(row = 0 ; row < matrixSize ; row++){
        for(col = 0 ; col < matrixSize ; col++){
            if(row == 0) {
                localMin[row][col] = matrix[row][col];
                continue;
            }
            left = (col-1 < 0) ? INT_MAX : localMin[row - 1][col - 1];
            mid = localMin[row - 1][col];
            right = (col+1 >= matrixSize) ? INT_MAX : localMin[row - 1][col + 1];
            min = (left < mid) ? left : mid;
            min = (min < right) ? min : right;
            localMin[row][col] = matrix[row][col] + min;
        }
    }
    for(row = matrixSize - 1, col = 0, min = INT_MAX ; col < matrixSize ; col++)
        min = (min < localMin[row][col]) ? min : localMin[row][col];
    return min;
}

## Complexity

|Space |Time |
|- |- |
|$O(N)$|$O(N)$|

## Result

- Runtime : 15 ms, 98.95%
- Memory : 6.7 MB, 27.37%