# はじめに
コーホート分析を用い日本の人口についてRで分析してみます。ここでは5年ごとの人口の推移を分析しています。今回はR言語を使用していますが、エクセルなどの表計算ツールでも手軽にできる分析です。
---
#### コーホート分析(Cohort Analysis)
コーホート分析(Cohort Analysis)とは、コーホート分析とは分析対象を共通して因子(ここでは年齢)で集団化し、時系列順に分析する手法です。ここでは人口の推移を分析していますが、マーケティングにおいて顧客のユーザーリテンション率などを表したりすることが多いです。例えばあるECサイトのログイン日を因子としてグループ化し、その後のリテンション率を日毎に可視化すると以下の図のようになります。
----
例えば4月1日にログインしたユーザーの35%は次の日に再度ログインしており、7日後には0%になっている事がわかります。また、4月4日に何かしらのイベント(介入)をしていたとして、**「イベントのおかげでログイン数が増え、リテンション率も高い数値を保っている。イベントは効果的だった」** という仮説がたてられます。
----

---
# 実装
早速実装してみます
使用するデータは日本政府が提供している <a href= "https://www.e-stat.go.jp/en">e-Stat</a> を使います。今回は1990~2005年の人口の推移について分析してみたいと思います。人口推移を年齢別に「生存率」をテーマに分析していきます。データによると、国勢調査は5年ごとに行われいるようなのでそちらを可視化します。要は上記で説明した、「ログイン日毎のリテンション率」を「年齢毎の生存率」と見立てて分析します。
----
### 使用ライブラリ
```r:setup
knitr::opts_chunk$set(echo = TRUE)
setwd('/Users/yokoishusei/Desktop/R/Summer_R/Week1')
library(datasets)
library(readxl)
library(dplyr)
library(tidyverse)
library(ggplot2)
source(gzcon(url('https://github.com/systematicinvestor/SIT/raw/master/sit.gz', 'rb')))
#setInternet2(TRUE)
library(tidyverse)
library(DT)
```
---
### データ加工
```r:raw_data
population = read_excel('05016.xls')
population = population %>%
select(3,5,seq(12,67,7)) %>%
slice(-c(1,2,4:10, 133:144))
population_each = population %>%
slice(-c(seq(3,117,6))) %>%
slice(-c(1:2)) %>%
slice(-101) %>%
select(-...3)
colnames(population_each) = c('age',population[1,c(3:10)])
colnames(population_each) = c('age','year_1920','year_1960','year_1970','year_1980','year_1990','year_1995','year_2000','year_2005')
population_1990to2005 = population_each %>%
select('age','year_1990','year_1995','year_2000','year_2005')
```
----
### データ加工 2
```r
population_1990to2005 = population_1990to2005 %>%
mutate(year_1990 = as.numeric(population_1990to2005$year_1990)) %>%
mutate(year_1995 = as.numeric(population_1990to2005$year_1995)) %>%
mutate(year_2000 = as.numeric(population_1990to2005$year_2000)) %>%
mutate(year_2005 = as.numeric(population_1990to2005$year_2005))
cohort_1990to2005 = population_1990to2005 %>%
mutate(year_1995 = as.numeric(lead(population_each$year_1995,5)))%>%
mutate(year_2000 = as.numeric(lead(population_each$year_2000,10)))%>%
mutate(year_2005 = as.numeric(lead(population_each$year_2005,15)))%>%
rename( 'age_at_1990' = 'age')
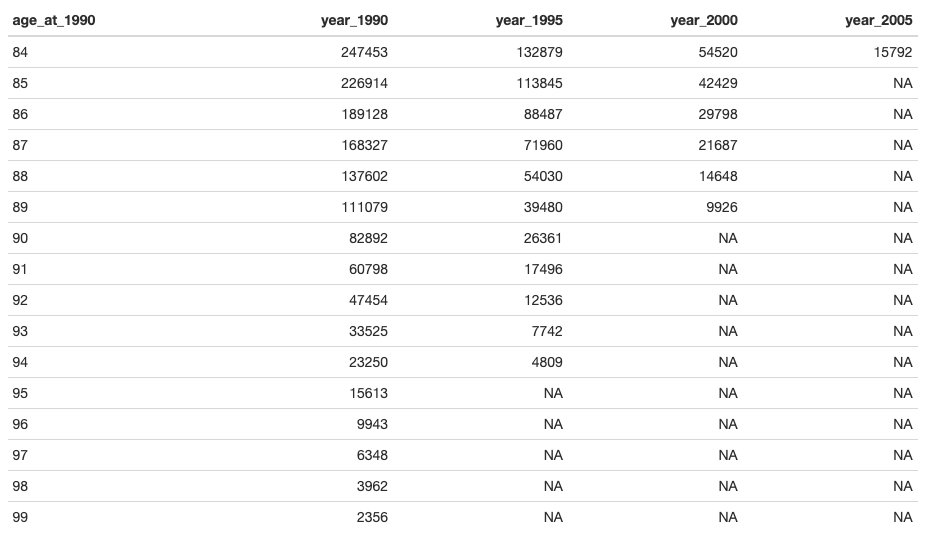
knitr::kable(tail(cohort_1990to2005,16))
```
----
出力された表をみると、1990に84歳だった247,453人の内、2005年には15,792人の方がご健全という事がわかります。
> 
---
### 可視化
上記の表を一番初めに紹介した様にパーセントに直し、色をつけてみやすくしたいと思います。パーセントの出し方は、各年の年齢毎の人口を0年目の数値で割るという手法になっています。
```r:cohort_1990to2005_pct
cohort_1990to2005_pct = data.frame(
cohort = cohort_1990to2005$'age_at_1990',
pop_1990 = cohort_1990to2005$year_1990, # pop at 1990
round(cohort_1990to2005[,3:ncol(cohort_1990to2005)] / cohort_1990to2005[["year_1990"]],3)*100 # divide eahc pop by pop_1990
)
DT::datatable(head(cohort_1990to2005_pct,100),
rownames = FALSE,
options = list(
pageLength = 8
))
temp = as.matrix(cohort_1990to2005_pct[65:95,])
rownames(temp) = as.character(paste(temp[,1],'_',temp[,2]))
temp = temp[,3:ncol(temp)]
colnames(temp) = paste( seq(1995,2005,5),'year', seq(5,15,5))
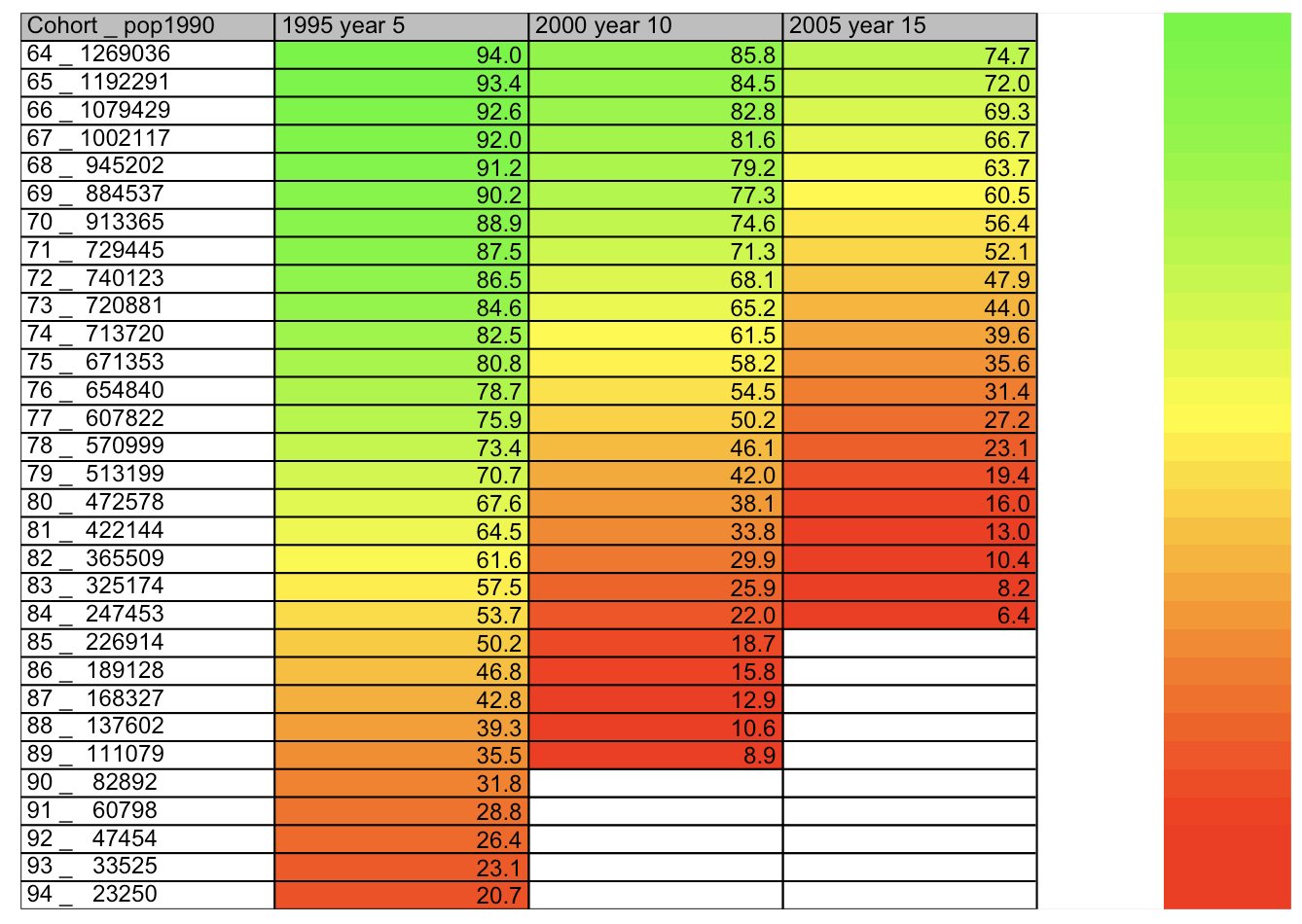
plot.table(temp,smain = 'Cohort _ pop1990', highlight = TRUE, colorbar = TRUE)
```
----
繰り返しになりますが、1990年の年齢で区切り、5年毎の生存率を表しています。綺麗なグラデーションはなだらかな変化を意味します。日本のような豊かな国はなだらかな人口推移をしている様です。
> 
---
# おわりに
5年ごとの人口の推移をコーホート分析を用いRで分析してみました。やはり、日本のような豊かな国はなだらかな推移が見られましたね。エクセルでも簡単に可視化できるので、お手頃な分析手法でもあします。ちなみに、上記の内容を英語でまとめて、かつ2010の人口推移を予測をしてみたりしたので、気になる方はぜひ見にきてやってください。
<a href = "https://github.com/Shusei25/skillset/tree/main/cohort_analysis">GitHub</a>
{"metaMigratedAt":"2023-06-17T06:22:59.092Z","metaMigratedFrom":"YAML","title":"【コーホート分析】初心者向け!Webマーケティングの強い味方!","breaks":true,"contributors":"[{\"id\":\"094bb48c-9fc0-4aef-8acb-a0e5dcbc1355\",\"add\":4324,\"del\":100}]"}