# Vzorce na fyziku

CC-BY
Vítek
Nina
Kája
Martin
Oggy
Tim
Matěj
Jenda

## Celkem staré vzorečky pro pro stejnosměrný proud

$$
R=\frac{U}{I}
$$
Ohmův zákon pro uzavřený obvod
$$
I = \frac{U_e}{R+R_i}
$$
$U_e$ = elektromotorické napětí (nezatíženého zdroje)
$R_i$ = vnitřní odpor zdroje
## Elektrická práce a výkon v obvodu *stejnosměrného* proudu

Práce $W$ [Joul]

Náboj $Q$ [Coulomb]

$$
W = UQ
$$

Pokud je elektrický proud konstantní, tak platí
$$
Q = It \qquad W = UIt
$$

Má-li vnější část odpor R, platí
$$
W=RI^2t=\frac{U^2}{R}t
$$

**Joulovo teplo** $Q_J$ je elektrická energie, který se přeměnila na teplo. Pokud obvod nedělá mechanickou nebo jinou práci, tak se všechna energie přemění na teplo a $Q_J=W=RI^2t=\frac{U\frac{Fe}{Q}2}{R}t$.

Výkon $P$ [**W**att] proudu ve spotřebiči o odporu $R$:
$$
P=\frac{W}{t}= UI=RI^2=\frac{U^2}{R}
$$

**Účinnost** $η$ (éta)[bezrozměrná] $= \frac{U}{U_e}$ ($U_e$ je elektromotorické napětí zdroje). Pomocí Ohmova zákona ji můžeme vyjádřit:
$$
\eta = \frac{R}{R+R_i}
$$
Z toho vyplývá, že účinnost je tím **větší, čím je větší odpor spotřebiče** v porovnání s **vnitřním odporem zdroje (Ri)**.

## Elektrické pole a jeho intenzita

- Ve vakuu:
$$
E = \frac{F_e}{Q} = k \cdot \frac{Q}{r^2}
$$
$k = \frac{1}{4πƐ_0} = 9 \cdot 10^9 \frac {Nm^2}{C^2}$ - konstanta úměrnosti
$F_e$ - elektrická síla
$E = [NC^{-1}]$ - intenzita elektrického pole

- V normálním prostředí:
$$
E= \frac{1}{4πƐ_0Ɛ_r} \cdot \frac{Q}{r^2}
$$
$r -$ vzdálenost mezi náboji
$Ɛ_r -$ relativní permitivita prostředí (pro vakuum $Ɛ_r = 1$, pro vše ostatní **>1**)
$Ɛ_0 -$ permitivita vakua ($Ɛ_0 =8,85\cdot 10^{-12} \frac{C^2}{Nm^2}$)

## Elektřina v pevných látkách

- Odpor ve vodiči:
$$
R = \rho \frac{l}{S}
$$

$\rho -$ rezistivita (měrný elektrický odpor) [$\Omega m$]
$l -$ délka vodiče
$S -$ povrch průřezu vodiče

(odpor rezistoru závisí na teplotě)

## Elektřina v kapalinách

- Závislost proudu na napětí v kapalině:
$$
I = \frac{U-U_r}{R}
$$

$U_r$ - rozkladné napětí

### Faradayovy zákony elektrolýzy

#### První Faradayův zákon
- Hmotnost vyloučené látky je přímo úměrná náboji, který prošel elektrolytem

$$
m = A \cdot Q = A \cdot I \cdot t
$$
$m$ - hmotnost látky
$Q$ - přenesený náboj
$I$ - proud
$t$ - čas

$A$ - elektrochemický ekvivalent látky (konstanta pro danou látku, zjistí se v tabulkách) - $[A] = kg \cdot C^{-1}$

#### Druhý Faradayův zákon
- Hmotnosti různých prvků (nebo radikálů) vyloučených při elektrolýze týmž celkovým nábojem jsou chemicky ekvivalentní

$$
m = \frac {M_m \cdot Q}{F \cdot \nu}
$$

$\nu$ [:ný:]- počet elementárních nábojů nutných pro vyloučení jedné molekuly
$M_m$ - molární hmotnost vyloučené látky
$Q$ - celkový náboj prošlý povrchem elektrody ($Q = I \cdot t$)
$F$ - Faradayova konstanta $$F = e \cdot N_a = 9,6487^{4} \cdot C \cdot mol^{-1}$$
- $e$ - elementární náboj
- $N_A$ - Avogadrova konstanta ($6,022 \cdot 10^{23} mol^{-1}$)

$$
N = \frac {Q}{\nu \cdot e }
$$
$N$ - počet vyloučených molekul

# Stacionární Magnetické pole

## Magnetická indukce
- **Magnetická síla**, když je vodič **kolmý k indukčním čarám**:
$$
F_m = B\cdot I \cdot l
$$
- $l$ - délka vodiče
$B$ - Magnetická indukce (silové působení magnetické pole na vodič)

- **Magnetická indukce**- charakterizuje velikost siločar
$$
B=\frac{F_m}{ I \cdot l}
$$

$[ B ] = \frac{N}{Am} =T$ (tesla)

- Když vodič **není kolmý k indukčním čarám**:
$$
|\vec{F_m}|=B\cdot I\cdot l \cdot \sin\alpha
$$
- $\alpha$ - odchylka vodiče a indukčních čar
$\vec{F_m}$ je kolmá na vodič

## Magnetické pole rovnoběžných vodičů s proudem

- Magnetická indukce pole **přímého vodiče**

$$
B=µ× \frac{I}{2πd}
$$

$d$ - vzdálenost od vodiče
$µ$ - permeabilita vakua

- u **dvou vodičů** (vzájemné působení vodičů)
$$
F_m=\frac{µ_0 I_1I_2}{2πd} \cdot l
$$
$d$ - vzdálenost dvou vodičů
$l$ - délka vodiče
$µ_0$ - permeabilita vakua ($4 \pi \cdot 10^{-7} N \cdot A^{-2}$)

### Permeabilita vakua

**µ [:mí:]** je konstanta, charakterizující magnetické vlastnosti prostředí, v němž existuje magnetické pole
$$
µ = µ_0 µ_r
$$

${µ_0}$ - permeabilita vakua

$$
{µ_0} = 4π · 10^{-7} N · A^{-2}
$$

${µ_r}$ - relativní permeabilita (pro vakuum ${µ_r} = 1$)

## Magnetické pole cívky

Solenoid = cívka se stejně hustými závity kruhového tvaru v celé délce cívky

uvnitř solenoidu:
$$
B = µ \cdot \frac{N\cdot I}{l}
$$
$N =$ počet závitů
$l =$ délka cívky

když má jenom jeden závit

$$
B = µ \cdot \frac{I}{2r}
$$

$r$ - poloměr závitu

## Magnetické vlastnosti látek
- Látky s vysokou permeabilitou **velmi** zesilují magnetické pole (µ ≥ 10)
- Ferromagnetické (železo, kobalt, nikl, )
- Látky, které ho mírně zesilují ( µ ≥ 1)
- Paramagnetické (Na, K, Al)
- Látky,s nízkou µ mírně zeslabují magnetický pole, protože elementární pole elektronů se vyruší (µ ≤ 1 )
- Diamagnetické (vzácné plyny, rtuť)

## Částice s nábojem v magnetickém poli

$$
\vec{F_m}=\vec{B} \cdot Q \cdot \vec{v} = \vec{B} \cdot e \cdot \vec{v}
$$
$v$ - rychlost částice
$B$ - magnetická indukce
$Q$ - celkový náboj ($Q = N \cdot e$ -> $N$ - počet částic)
$e$ - elementární náboj (náboj **jednoho** elementu) ($e = 1,602 \cdot 10^{-19} C$)

$$
r = \frac {m \cdot v}{e \cdot B}
$$
$r$ - poloměr trajektorie elektronu (částice)
$m$ - hmotnost elektronu ($m = 9,1 \cdot 10^{-31} kg$)
$v$ - rychlost částice
$e$ - náboj částice
$B$ - magnetická indukce

# Nestacionární magnetické pole
$$
\vec{B} \ne K
$$

- Vzniká indukované magnetické pole
- Magnetická indukce se mění s časem -> **není konstantní**

## Magnetický indukční tok

$$
\Phi = \vec{B} \cdot S \cdot \cos \alpha
$$
$\Phi$ - magnetický indukční tok - $[\Phi] =$ Wb (weber)
$B$ - magnetická indukce
$S$ - plocha (na kterou působí magnetická indukce)
$\alpha$ - úhel, který magnetická indukce (B) svírá s normálou (kolmá čára k rovině)

- S **jedním** závitem:
$$
\Phi = \vec{B} \cdot S \cdot \cos{\omega t}
$$
$B$ - magnetická indukce
$S$ - plocha (na kterou působí magnetická indukce)
$\omega$ - úhlová rychlost (kterou se daný závit otáčí)
$t$ - čas

- S **více** závity (N je počet závitů):
$$
\Phi = \vec{B} \cdot S \cos{\omega t} \cdot N
$$

### Lorentzova síla
- https://cs.wikipedia.org/wiki/Lorentzova_s%C3%ADla
- pro el. a mag. pole

$$
Fe = Q \cdot E
$$

$Q$ - náboj
$E$ - intenzita pole

$$
\vec{F_z}=\vec{F_e} + \vec{F_m}
$$

- po přímce

$$
|\vec{F_e}|=|\vec{F_m}|
$$

## Lenzův zákon
> Indukovaný elektrický proud v uzavřeném obvodu má takový směr, že svým magnetickým polem působí proti změně magnetického indukčního toku, která je jeho příčinou.
- **Určuje směr** indukovaného proudu, který vzniká v cívce **při elektromagnetické indukci**
- Indukovaný proud působí proti změně magnetického pole
- **Sepnutí obvodu** (zvýšení proudu) - **odpuzení** hlníkového prstence:
- **Rozpojení obvodu** (snížení proudu) - **přitažení** hlníkového prstence:

## Faradayův zákon elmg. indukce
- Změní-li se **magnetický indukční tok ($\Delta \Phi$)** za **čas ($\Delta t$)**, vzniká **indukované elektromotorické napětí ($U_i$)**, jehož střední hodnota je:

$$
U_i = - \frac {\Delta \Phi}{\Delta t}
$$
- oddělení vzorečků 🙃

---

$$
U_i = - \frac{\Delta \vec{B} \cdot \vec{S}}{\Delta t} = \frac {\partial B \cdot S \cdot \cos \omega t}{\partial t}
$$

$$
U_i = B \cdot S \cdot \omega \cdot \sin \omega t
$$

$$
U_i = \frac {\Delta B \cdot l \cdot b}{\Delta t}
$$

$$
U_i = B \cdot l \cdot \frac {\Delta b}{\Delta t}
$$

$$
U = B \cdot l \cdot v
$$

## Přechodný děj
- Přechodný děj = děj, ke kterému dochází při spojení nebo rozpojení elektrického obvodu, pokud se v obvodu nachází cívka s velkou indukčností L


- **při sepnutí** obvodu vzniká indukované napětí **opačné** polarity než je napětí zdroje
- **při rozpojení** obvodu vzniká indukované napětí **stejné** polarity, jako má zdroj, ale **značně větší velikosti**

$$
I =\frac{U_e + U_i}{R} = \frac {U_e - L \cdot \frac{\Delta I}{\Delta t}}{R}
$$
$I$ - proud
$U_e$ - elektromotorické napětí zdroje
$U_i$ - indukované napětí
$L$ - indukčnost
$R$ - odpor

$$
E_m = \frac{1}{2} \cdot L\cdot I^{2}
$$
$E_m$ - energie magnetického pole cívky

## Střídavý proud
$$
u = \frac {\Delta \phi}{\Delta t}
$$
$u$ - **okamžitá** hodnota napětí
$\Delta \phi$ - magnetický indukční tok
$\Delta t$ - čas

$$
u = U_m \sin(ωt)
$$
$U_m$ - amplituda napětí
$\omega$ - úhlová rychlost ($\omega = 2 \pi f$)

$$
i = I_m \cdot \sin (\omega t)
$$
$i$ - **okamžitá** hodnota proudu
$I_m$ - amplituda proudu

- Polarita napětí se periodicky mění a tomu odpovídá i změna proudu

## Obvod střídavého proudu
### S odporem (s rezistorem)
$R$ - rezistance ...ohm[Ω]
- Proud kopíruje napětí (jsou ve fázi, fázový rozdíl je nulový)

### S indukčností (s cívkou)
- Proud procházející cívkou generuje měnící se magnetické pole
- Na cívce se indukuje napětí opačné polarity než na zdroji
- Proud se zpožďuje za napětím
- Fázový rozdíl je: $\frac{\pi}{2}$
- Časový rozdíl je: $\frac {T}{4}$ ($T$ - perioda)

$$
X_L = \frac {U_m}{I_m} = L . \omega
$$
$X_L$ - Induktance…ohm[Ω]
$L$ - Indukčnost.. henry
$U_m$ - amplituda napětí
$I_m$ - amplituda proudu

### S kapacitou (s kondenzátorem)
- Kapacita kondenzátoru se vybijí a nabijí
- Mezi deskami kondenzátoru neprobíhá proud
- napětí a proud nejsou ve fázi
- napětí se opožďuje za proudem o $\frac {\pi}{2}$
- fázový rozdíl je $- \frac{\pi}{2}$

$$
X_c =\frac{1} {\omega \cdot C}
$$
$X_c$ - Kapacitance $[X_c] = \Omega$ (ohm)
$C$ - kapacita kondenzátoru $[C] = F$ (farad)
$\omega$ - úhlová rychlost ($\omega = 2 \pi f = \frac {2 \pi}{T}$)

- reaktance je rozdíl indiuktance minus kapacitance

### Složený obvod střídavého proudu (s RLC v sérii - aneb mix výše uvedeného)
$$
Z = \sqrt{R^2 + (Lω - \frac{1}{ωc})^2} = \frac {U_m}{I_m}
$$

$Z$ - **Impedance** (v Ohmech) - celkový odpor složek v sérii

### Rezonance
- když se induktance = kapacitanci ( $X_L = X_c$) -> $Z = R$
- dochází k tomu při určité frekvenci
- **Rezonanční frekvence**
$$
f_{rez} = \frac{1} {2π {\sqrt{L \cdot C }}}
$$
$f_{rez}$ - rezonanční frekvence
$L$ - indukčnost
$C$ - kapacita

## Výkon střídavého produ s impedancí
- Ovlivněn fázovým rozdílem mezi napětím a proudem v obvodu
- V části obvodu se přeměňuje na teplo na magnetické pole a na elektrické pole

$$
P = U_e\cdot I_e\cdot cos \ φ
$$

$P$ - činný výkon

$U_e$ - efektivní hodnota napětí
$U_{ef} = U_{max} \sqrt{\frac{1}{\pi}\int_{0}^{\pi} \sin^2(t)\, \mathrm{d}t} = \frac {U_{max}} {\sqrt{2}}$

$I_e$ - efektivní hodnota proudu
$I_{ef} = I_{max} \sqrt{\frac{1}{\pi}\int_{0}^{\pi} \sin^2(t)\, \mathrm{d}t} = \frac {I_{max}} {\sqrt{2}}$

$φ$ - fázový rozdíl mezi napětím a proudem
$cosφ$ - účiník

- **Efektivní napětí**- Napětí pomyslného stejnosměrného proudu, určené tak aby při proudu střídavém zůstal výkon stejný
- **Efektivní proud** - Efektivní hodnota střídavého proudu je hodnota proudu stejnosměrného, který v daném obvodu vykoná za stejný čas stejnou práci jako proud střídavý

- určuje účinnost přenou energie ze zdroje střídavého proudu do spotřebiče
- činný výkon odpovídá té části el. energie, která se v obvodu za jednotku času mění v teplo nebo užitečnou prácí, nikoliv energii pole

## Výkon střídavého proudu s rezistancí
- **Stejnosměrný** proud
$$
P = U \cdot I = R \cdot I^2
$$

$P$ - výkon
$U$ - napětí
$I$ - proud

- **Střídavý** proud
$$
p = R \cdot i^2 = R \cdot I_m^2 \cdot sin^2ωt
$$

$p$ - **okamžitý** výkon
$R$ - odpor
$i$ - **okamžitý** proud
$I_m$ - amplituda proudu
$\omega$ - úhlová rychlost
$t$ - čas

$$
W = \frac {1}{2} P_{max} \cdot t = \frac {1}{2} \cdot R \cdot I_m^2
$$
$W$ - práce
$P_{max}$ - maximální výkon

$$
P_{střední} = \frac {W}{T} = \frac{1}{2} \cdot R \cdot l_m^2
$$

## Sdružené napětí

- napětí mezi fázovými vodiči

$$
U_s = \sqrt{3} \cdot U_1
$$

- Na vytvoření se podílejí dvě fáze proti sobě a jeho velikost spočítáme vektorovým součtem napětí jedné fáze a obráceného napětí druhé fáze
- Trojfázová soustava napětí
- Zapojení do hvězdy (220V) nebo trojúhelníku (380-400V)

[odkaz na obrázky a další vzorečky](http://elektro.fs.cvut.cz/ZS/stare0304/2141015.pdf/papezova/trojfaz_slejdy.pdf)

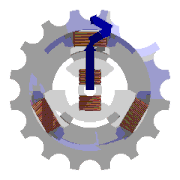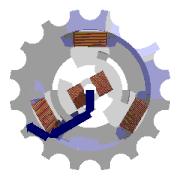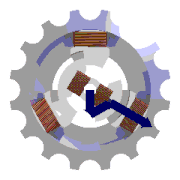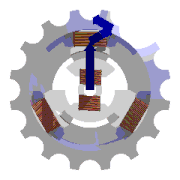
## Elektromotor
- skládá se z dvou částí:
stator - 3 cívky - 120°, indukuje se napětí
rotor- asynchronní, elektromagnet, 50 Hz

- $s$ - **skluz**, udává se v procentech (cca 1%)
$$
s= \frac {f_{pole} - f_{rotor}}{f_{pole}}
$$


## Transformátor
- reguluje (mění) napětí v síti
- primární a sekundární cívky, navinuté na společné jádro
- napětí na sekundární cívce je posunuté o 180° než na primární cívce

$$
\frac{U_2}{U_1} = \frac{N_2}{N_1} = k
$$

$k$ - tranformační poměr
počty závitů na primární ($N_1$) a sekundární ($N_2$) cívce

$$
U_1 I_1 = U_2 I_2
$$

- přenos elektrické energie - dálkový přenos se uskutečňuje při velmi vysokém napětí (až 400k V)

$$
P_{ztrát} = R_{sítě} \cdot I^2
$$

## Tranzistor

- Zesiluje proud
- Dva přechody, NPN nebo PNP

$E$ - emitor (krajní)
$B$ - báze (uprostřed)
$C$ - Kolektor (krajní)


- **Tranzistorový jev** - malé napětí vzbuzuje v prostoru báze proud, který je příčinou vzniku mnohem většího proudu $I_c$ (proud kolektoru)

$\beta$ - proudový zesilovací činitel

$$
\beta = \frac{\Delta I_C}{\Delta I_B}
$$

## Elektromagnetické kmitání a vlnění

-elg. oscilátor

# Návod jak to psát markdown + LaTeX

tohle je obyčejný text

do dolarů se píšou LaTeX vzorce
$$
\frac{1}{2x^2} = F_g
$$

odkaz na další věci vypadá [takhle](https://www.markdownguide.org/basic-syntax/)

### Hashkřížkama se dělaj nadpisy

### užitečné LaTeX věci

zlomek:
$$
\frac{5}{6}
$$

násobení jako tečka:
$$
5 \cdot 3
$$

mocnina (horní index):
$$
x^2 = 4
$$
$$
x^{\frac{1}{2}} = \sqrt{2}
$$

doní index:
$$
F_g = F_{odstředivá}
$$

Vektor:
$$
\vec{n}
$$

další znaky:
$$
\sqrt{5 \cdot 3 \pi + \Phi \div \phi - \omega}
$$

$$
÷×
$$

$$
\frac {3}{4}
$$