# Whitehacks 2022 All Crypto Challenge Writeups
Author: Bennett Lim
# Crypto / Really S1mp(l3) Algorithm
## Challenge Description
```
Really S1mp(l3) Algorithm
135
CRYPTO
72 SOLVES
DESCRIPTION
Author: xbowery
Difficulty: Easy
Rumour has it that this algorithm originated from the Republic of South Africa!
ATTACHED FILES
challenge.txt
```
**challenge.txt**
```
This is really simple. I hope you can solve it.
p = 89677525768054651799811339393073439598902155753884683756875620558829954902529
q = 84438062750417241222463359000671279258755386034358736244893269480285225711041
e = 65537
ct = 2006481391032768131106572837821981606814991526844317992631122301790966354846642917808142106585149537517169168108747108233658443914026685951141453359021205
```
## Challenge Summary
This is a simple RSA starter challenge, where we have to decrypt ``ct``, with ``p``, ``q``, and ``e`` being known.
## Solution
Following [this Wikipedia article](https://en.wikipedia.org/wiki/RSA_(cryptosystem)#Key_generation), since ``p`` and ``q`` (which are normally supposed to be kept secret) are given to us, we can easily calculate the private key, ``d``, and use it to decrypt ``ct`` and get the plaintext, ``pt``, which contains the flag.
Step 1: Calculate ``phi``, which is equal to ``(p-1)*(q-1)``, since in this case, ``p`` is not equal to ``q``.
Step 2: Calculate ``d``, which is equal to ``inverse_mod(e, phi)`` (i.e. the modular inverse of ``e`` mod ``phi``).
Step 3: Calculate ``pt``, which is equal to ``pow(ct, d, n)`` (i.e. ``ct^d`` mod ``n``).
Step 4: Convert ``pt`` from an integer to bytes.
**Script**
```sage
def intToBytes(x):
x = Integer(x)
return int.to_bytes(int(x), (x.nbits()+7)//8, 'big')
p = 89677525768054651799811339393073439598902155753884683756875620558829954902529
q = 84438062750417241222463359000671279258755386034358736244893269480285225711041
e = 65537
ct = 2006481391032768131106572837821981606814991526844317992631122301790966354846642917808142106585149537517169168108747108233658443914026685951141453359021205
n = p*q
phi = (p-1)*(q-1)
d = inverse_mod(e, phi)
pt = pow(ct, d, n)
print(intToBytes(pt))
```
**Output**
```
b'WH2022{1t5_r34lly_s1mpl3_4m_1_r1ght}'
```
# Crypto / The Indecipherable Cipher
## Challenge Description
```
The Indecipherable Cipher
441
CRYPTO
55 SOLVES
DESCRIPTION
Author: WickedEye (Ying Keat)
Difficulty: Easy
Some say this cipher cannot be deciphered. Well, do you believe them?
Even worse, some say this cipher is misattributed!
I would say that the key to solving this challenge is to remember who the true inventor was.
ATTACHED FILES
cipher.txt
```
**cipher.txt**
```
CP2022{j1b3n3e3_15_Pcn_Xa3f@x_K1dC3R_0A_yB3F01Ys}
```
## Challenge Summary
We are supposed to undo a cipher that has been applied to the flag.
## Solution
An attempt was made to decode the ciphertext by using [CyberChef's Magic Mode](https://gchq.github.io/CyberChef/#recipe=Magic(3,true,false,'')&input=Q1AyMDIye2oxYjNuM2UzXzE1X1Bjbl9YYTNmQHhfSzFkQzNSXzBBX3lCM0YwMVlzfQ), [dCode's Cipher Identifier](https://www.dcode.fr/cipher-identifier), and [Boxentriq's Cipher Identifier](https://www.boxentriq.com/code-breaking/cipher-identifier). However, none of these tools were able to decode the ciphertext automatically.
After doing some Googling with the search query "The Indecipherable Cipher", it was found that "The Indecipherable Cipher" refers to the "Vigenère cipher", which requires a key in order to decode the ciphertext.
Going back to the challenge description, the key is hinted to be the inventor of the Vigenère cipher, who is [Giovan Battista Bellaso](https://en.wikipedia.org/wiki/Vigen%C3%A8re_cipher).
Testing out his first name, ``Giovan`` as the key, we [successfully manage](https://gchq.github.io/CyberChef/#recipe=Vigen%C3%A8re_Decode('Giovan')&input=Q1AyMDIye2oxYjNuM2UzXzE1X1Bjbl9YYTNmQHhfSzFkQzNSXzBBX3lCM0YwMVlzfQ) to get the flag, ``WH2022{v1g3n3r3_15_Juz_Ca3s@r_C1pH3R_0N_sT3R01Ds}``.
# Crypto / The Poem of Knowledge
## Challenge Description
```
The Poem of Knowledge
767
CRYPTO
40 SOLVES
DESCRIPTION
Author: xbowery
Difficulty: Easy
Our knowledgeable alien friend named Beale left us with a purported "Poem of Knowledge" before he went back to his universe.
He also dropped a message behind. Can you decipher what he was trying to say?
17-73-24-55-84-101-141-44-54-49-10-123-62-131-114-67-47-46-60-83-84
Note: Please wrap the flag with WH2022{...}
The flag is case-sensitive!
ATTACHED FILES
Poem Of Knowledge.txt
```
**Poem Of Knowledge.txt**
```
The Road Not Taken
By Robert Frost
Two roads diverged in a yellow wood,
And sorry I could not travel both
And be one traveler, long I stood
And looked down one as far as I could
To where it bent in the undergrowth;
Then took the other, as just as fair,
And having perhaps the better claim,
Because it was grassy and wanted wear;
Though as for that the passing there
Had worn them really about the same,
And both that morning equally lay
In leaves no step had trodden black.
Oh, I kept the first for another day!
Yet knowing how way leads on to way,
I doubted if I should ever come back.
I shall be telling this with a sigh
Somewhere ages and ages hence:
Two roads diverged in a wood, and I—
I took the one less traveled by,
And that has made all the difference.
```
## Challenge Summary
We are supposed to obtain the flag from a sequence of integers and a text file containing a poem, suggesting some form of book cipher.
## Solution
Based on the challenge description, we are given a hint from the name "Beale". Googling this name leads us to the [Beale Cipher](https://en.wikipedia.org/wiki/Beale_ciphers).
An attempt was made using [dCode's Beale Cipher](https://www.dcode.fr/book-cipher) to extract the message, which was successful, as it returned ``IHOPEYOUHADAGREATTIME``.
Unfortunately, that is not the right message, as the flag is case-sensitive. As such, a custom case-sensitive version of Beale's cipher was scripted:
**Script**
```py
f = open("Poem Of Knowledge.txt", "r")
ct = [17,73,24,55,84,101,141,44,54,49,10,123,62,131,114,67,47,46,60,83,84]
corpus = f.read()
#Strip new lines, extra spaces, etc.
corpus = corpus.replace('\r', ' ').replace('\n', ' ')
corpus = corpus.replace(' ', ' ')
print(corpus)
#Generate array of words
words = []
buf = ""
for i in range(len(corpus)):
if corpus[i] == ' ':
words.append(buf)
buf = ""
else:
buf += corpus[i]
if buf != "":
words.append(buf)
#Beale's cipher (case sensitive)
flag = ""
for i in range(len(ct)):
flag += words[ct[i]-1][0]
print(flag)
```
**Output**
```
The Road Not Taken By Robert Frost Two roads diverged in a yellow wood, And sorry I could not travel both And be one traveler, long I stood And looked down one as far as I could To where it bent in the undergrowth; Then took the other, as just as fair, And having perhaps the better claim, Because it was grassy and wanted wear; Though as for that the passing there Had worn them really about the same, And both that morning equally lay In leaves no step had trodden black. Oh, I kept the first for another day! Yet knowing how way leads on to way, I doubted if I should ever come back. I shall be telling this with a sigh Somewhere ages and ages hence: Two roads diverged in a wood, and I— I took the one less traveled by, And that has made all the difference.
IHopeYouhadagreattime
```
Therefore, the flag is ``WH2022{IHopeYouhadagreattime}``.
# Crypto / Ridiculously Simpler Algorithm
## Challenge Description
```
Ridiculously Simpler Algorithm
976
CRYPTO
14 SOLVES
DESCRIPTION
Author: xbowery
Difficulty: Medium
You cracked me once, now I'm back for revenge with an upgraded defence mechanism!
ATTACHED FILES
encrypted.txt
```
**encrypted.txt**
```
This is supposedly even simpler. Try me!
n = 10737815683051749791647908968171036410193052055925978453198599402338822997173859289423308183048750681303695147135467822832842221572174477705930888427996441
e = 65537
c = 2025103500488147486354827835413388045219955669590787897403050967001645770151549545526845887271487454606326620556228871888382889102118986522714812376848980
```
## Challenge Summary
This is a "more standard" RSA challenge, where we have to decrypt ``ct``, with only the public key parameters, ``n`` and ``e`` being known.
Unlike the previous challenge, we are no longer provided with ``p`` and ``q``.
## Initial Analysis
Since the public exponent is the standard RSA public exponent ``e = 65537``, we can make the assumption that there is no vulnerability related to the public exponent. This implies that the vulnerability in this RSA public key must have something to do with ``n`` instead.
This suspicion is confirmed when we try to factorize ``n`` using [FactorDB](http://factordb.com/index.php?query=10737815683051749791647908968171036410193052055925978453198599402338822997173859289423308183048750681303695147135467822832842221572174477705930888427996441), which shows that ``n`` is a perfect square.
Since ``n`` is a perfect square, this means that ``p = q``, and ``n = p^2``. Therefore, we can calculate ``p = q = sqrt(n)``.
From there, we can try and decrypt ``ct``, using the steps described previously for Really S1mp(l3) Algorithm (the only difference is ``phi = p*(p-1)``, since ``p = q``).
**Script**
```sage
def intToBytes(x):
x = Integer(x)
return int.to_bytes(int(x), (x.nbits()+7)//8, 'big')
n = 10737815683051749791647908968171036410193052055925978453198599402338822997173859289423308183048750681303695147135467822832842221572174477705930888427996441
e = 65537
c = 2025103500488147486354827835413388045219955669590787897403050967001645770151549545526845887271487454606326620556228871888382889102118986522714812376848980
p = sqrt(n)
assert p^2 == n
phi = p*(p-1)
d = inverse_mod(e, phi)
pt = pow(c, d, n)
assert pow(pt, e, n) == c
print(pt)
print(intToBytes(pt))
```
**Output**
```
87725048505012310448119951005211451951214811795991145299107951095195116119499951125
b'\x0b\x8fhN.>`k\xe5-\xed\xfb\xac\x91\xfa\xf4\xf1\xdd\xe8X\xd5\xc5\x0f\xf7\x01\x06H\xa4\x9d\x19\xd6V;L\x15'
```
Although we were able to successfully calculate ``pt``, given that the assertion ``pow(pt, e, n) == c`` is true (we do this to ensure that we didn't make any mistakes in the computation of ``phi``, ``d``, and ``pt``), the ``intToBytes()`` output does not provide us with the flag.
This suggests that ``pt`` may be encoded via some cipher which we need to undo before we can get the flag.
## Decoding pt
After some testing, it was found that the start of the integer, ``877250485050`` suspiciously matches the flag format when [converted to decimal](https://gchq.github.io/CyberChef/#recipe=To_Decimal('Space',false)&input=V0gyMDIy) (``WH2022`` is equivalent to ``87 72 50 48 50 50``).
Therefore, the flag can be obtained by splitting the integer manually to ``87 72 50 48 50 50 123 104 48 119 95 100 52 114 51 95 121 48 117 95 99 114 52 99 107 95 109 51 95 116 119 49 99 51 125``, which is equivalent to ``WH2022{h0w_d4r3_y0u_cr4ck_m3_tw1c3}``.
The splitting should be done such that each integer segment is within the range ``[32, 126]`` inclusive (i.e. the [printable ASCII character range](https://www.asciitable.com/)).
## Automated Decoding of pt?
After the CTF, I found out of [this tool](https://onlineasciitools.com/convert-decimal-to-ascii) which uses heuristics to perform the integer splitting process mentioned above:

Alternatively, one can also consider writing a recursive backtracking function to split the integer. This script has the added benefit of printing out all possible integer splits (in the event where there are more than one possible valid ways to split the integer).
**Script**
```py
s = "87725048505012310448119951005211451951214811795991145299107951095195116119499951125"
buf = []
def f(pos):
if pos == len(s): #Valid, print buf
print(buf)
return
if pos+2 <= len(s) and int(s[pos:(pos+2)]) >= 32: #Can get 2 chars, and the 2 chars' int value >= 32
buf.append(int(s[pos:(pos+2)]))
f(pos+2)
buf.pop()
elif pos+3 <= len(s) and int(s[pos:(pos+3)]) <= 126: #Can get 3 chars, and the 3 chars' int value <= 126
buf.append(int(s[pos:(pos+3)]))
f(pos+3)
buf.pop()
f(0)
```
**Output**
```
[87, 72, 50, 48, 50, 50, 123, 104, 48, 119, 95, 100, 52, 114, 51, 95, 121, 48, 117, 95, 99, 114, 52, 99, 107, 95, 109, 51, 95, 116, 119, 49, 99, 51, 125]
```
# Crypto / Meet where? Middle Road?
## Challenge Description
```
Meet where? Middle Road?
988
CRYPTO
7 SOLVES
DESCRIPTION
Author: WickedEye (Ying Keat)
Difficulty: Medium-Hard
My lecturer told me that DES is not secure and I should use AES for encryption.
Here's what I have as part of my school project to securely encrypt messages on where to meet my friends. I am sure no one can crack AES encryption.
Challenge Access:
nc challenges1.whitehacks.xyz 41337
nc challenges2.whitehacks.xyz 41337
ATTACHED FILES
secure_aes.py
```
**secure_aes.py**
```py
from random import randint
from base64 import b64encode
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
AES_KEY_SIZE = 16
flag = b"WH2022{fake_flag_for_testing}"
# Some say 0 is not a good number.
def get_new_key() -> bytes:
digits = b"123456789"
fav_event = b"wH1t3H@cK5_"
while len(fav_event) < AES_KEY_SIZE:
fav_event += bytes([digits[randint(0, 8)]])
return fav_event
# Encrypting twice will make AES even stronger!
def encrypt(data, key1, key2):
cipher1 = AES.new(key1, mode=AES.MODE_ECB)
ct = cipher1.encrypt(pad(data, AES.block_size))
cipher2 = AES.new(key2, mode=AES.MODE_ECB)
ct = cipher2.encrypt(ct)
ct = b64encode(ct).decode("utf-8")
return ct
def solve_me():
key1 = get_new_key()
key2 = get_new_key()
ct = encrypt(flag, key1, key2)
print(
"Welcome to my personal encryption project\n"
+ "Where to meet next:\n"
+ ct
+ "\n\nTest out this secure encryption scheme:\n> ",
end="",
)
try:
pt = input().strip()
custom_enc = encrypt(pt.encode("utf-8"), key1, key2)
print(custom_enc + "\n")
exit(1)
except Exception as e:
print(e)
print("Error!\n")
exit(1)
if __name__ == "__main__":
solve_me()
```
## Challenge Summary
In essence, this server uses a custom AES encryption function, which works by encrypting data twice (in ECB mode) using 2 keys, ``key1`` and ``key2`` (that are randomly generated every time we connect to the server).
Each key has the format ``wH1t3H@cK5_*****``, where ``*`` represents a digit from ``'1'`` to ``'9'`` inclusive (``'0'`` is excluded).
The server provides us the flag encrypted using ``key1`` and ``key2``, and allows us to make a single encryption using the same keys (``key1`` and ``key2``), and will provide us with the ciphertext.
## ECB Vulnerabilties?
When considering AES vulnerabilities, the AES mode of operation (e.g. ECB, CBC, etc.) is often an important factor to consider when exploring possible exploits.
In particular, the ECB mode of AES is known to have quite a few vulnerable properties, as mentioned in [this post](https://crypto.stackexchange.com/a/20946).
For our purposes, the ability to "detect whether two ECB-encrypted messages are identical" is the most critical.
## What About Brute Force?
AES keys are supposed to be randomly generated so as to ensure secure encryption, and prevent the attacker from guessing the key.
However, for this challenge, ``get_new_key()`` returns keys of a specific format. Since there are only 5 bytes that are randomly generated, with each byte being a digit from ``'1'`` to ``'9'`` inclusive, there are only ``n = 9^5 = 59,049`` possible keys that can be returned by ``get_new_key()``.
This search space is extremely small, considering how a normal 16 byte AES key with randomly chosen bytes indicates ``256^16 = 3.40*10^38`` possible keys.
Although the search space is small for a single key, since we have to figure out both keys in order to decrypt the flag, we would still have to search through ``n^2 = 3,486,784,401`` possible combinations for ``key1`` and ``key2``, which is infeasible.
If we let ``n = 9^5``, this algorithm can be said to have an (average) time complexity of O(n^2), and space complexity of O(1).
## Meet in the Middle (MITM) Attack
Recall: We can send a single plaintext (that we 100% control) to the server, and get the ciphertext that is encrypted twice with ``key1`` followed by ``key2``.
**Server's Encryption Scheme**
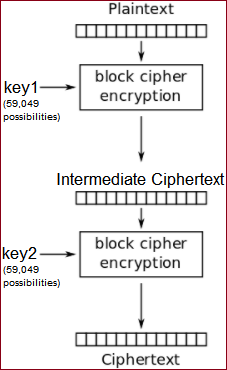
**Idea**
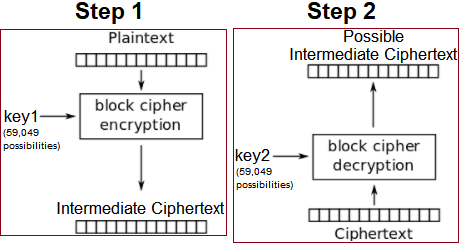
We can generate all possible intermediate ciphertexts using all possible keys for ``key1``, and store all intermediate ciphertext -> key mappings in a hashmap.
Afterwards, we can try and decrypt the ciphertext from the server using all possible keys for ``key2``.
If the decryption result (represented as possible intermediate ciphertext) matches some intermediate ciphertext stored in the hashmap, we have successfully leaked ``key1`` and ``key2``.
By using this MITM Attack, the (average) time complexity is reduced from O(n^2) to O(n), with space complexity increasing from O(1) to O(n).
Once we have leaked ``key1`` and ``key2``, we can simply use them to decrypt the flag ciphertext provided at the start of the connection, and get the flag.
**MITM Attack Scheme**
## Complete Script
Implementation Note: For this challenge, _any_ plaintext with length less than 16 will work (for the sake of simplicity, do not choose a plaintext that is 16 bytes or longer, as this will lead to the use of multiple AES blocks, un-necessarily complicating the script).
**Script**
```py
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from pwn import *
import random
#Get data from server
def genRandStr(): #Returns a random string consisting of uppercase and lowercase alphabets of length in range [1, 16)
return ''.join(random.choice(string.ascii_letters) for _ in range(random.randrange(1, 16)))
r = remote("challenges1.whitehacks.xyz", 41337)
CT = None
for i in range(5):
s = r.readline()
print(s)
if i == 2:
CT = base64.decodebytes(s) #Get the flag ciphertext
print("Flag CT", CT)
CHOSEN_PT = genRandStr().encode() #Randomly generate a plaintext string
print("Chosen PT", CHOSEN_PT)
r.sendline(CHOSEN_PT)
PADDED_CHOSEN_PT = pad(CHOSEN_PT, AES.block_size)
s = r.readline()
print(s)
TARGET = base64.decodebytes(s[2:]) #Get the ciphertext of the randomly generated plaintext string
print("Chosen PT's Ciphertext", TARGET)
#Retrieve flag from MITM Attack
fav_event = "wH1t3H@cK5_"
valid_keys = []
for i in range(100000): #Generate all possible keys
s = str(i).zfill(5) #Ensure number is properly padded
if "0" not in s:
valid_keys.append(str.encode(fav_event + s))
print(len(valid_keys))
mp = dict()
for i in range(len(valid_keys)): #Generate all possible intermediate ciphertexts
cipher = AES.new(valid_keys[i], mode=AES.MODE_ECB)
ct = cipher.encrypt(PADDED_CHOSEN_PT)
mp[ct] = valid_keys[i]
for i in range(len(valid_keys)): #Test all keys for key2
cipher = AES.new(valid_keys[i], mode=AES.MODE_ECB)
pt = cipher.decrypt(TARGET)
if pt in mp: #Decryption result matches an intermediate ciphertext
key2 = valid_keys[i]
key1 = mp[pt]
print("Leaked", key1, key2)
break
cipher1 = AES.new(key1, mode=AES.MODE_ECB) #Use leaked key1 and key2 to decrypt the flag ciphertext
cipher2 = AES.new(key2, mode=AES.MODE_ECB)
print(cipher1.decrypt(cipher2.decrypt(CT)))
```
**Sample Output**
```
b'Welcome to my personal encryption project\n'
b'Where to meet next:\n'
b'yoaNQm5736nIEWT9VE3TJgAlq51D53jDDHJVDXi+ymVYZHsuZ1//vQzp76U3zYhH\n'
Flag CT b'\xca\x86\x8dBn{\xdf\xa9\xc8\x11d\xfdTM\xd3&\x00%\xab\x9dC\xe7x\xc3\x0crU\rx\xbe\xcaeXd{.g_\xff\xbd\x0c\xe9\xef\xa57\xcd\x88G'
b'\n'
b'Test out this secure encryption scheme:\n'
Chosen PT b'AOVAYBJR'
b'> ZcZTUIHu3CkSRIKtYmlZCg==\n'
Chosen PT's Ciphertext b'e\xc6SP\x81\xee\xdc)\x12D\x82\xadbiY\n'
59049
Leaked b'wH1t3H@cK5_25865' b'wH1t3H@cK5_24699'
b'WH2022{M1dDl3_R0@d_15_tH3_b3sT_pLAc3_2_m33T}\x04\x04\x04\x04'
```
# Crypto / Booleancrypt
## Challenge Description
```
Booleancrypt
1000
CRYPTO
2 SOLVES
DESCRIPTION
Author: prokarius
Difficulty: Hard
This little fellow seems to be in charge of their encryption module, here are his insides!
Challenge Access:
nc challenges1.whitehacks.xyz 43232
nc challenges2.whitehacks.xyz 43232
ATTACHED FILES
booleancrypt.py
```
**Hint from Challenge Author (on Discord)**
> Erm... Hint: Is there a way to distinguish between the 8 random functions? From there, study the functions, does any of the functions leak any information?
**booleancrypt.py**
```py
#!/usr/bin/python3
import os
import random
import base64
Not = lambda x: 255-x
Or = lambda x,y:x|y
And = lambda x,y:x&y
xor = lambda x,y:x^y
nor = lambda x,y:Not(x|y)
nand= lambda x,y:Not(x&y)
xnor = lambda x,y:Not(x^y)
xand = lambda x,y:Not(x&y)&(x&y) # Exclusive AND...? Returns true if x and y are true, except when they are, then retrun false...?
xnand = lambda x,y:Not(x&y)|(x&y) # Exclusive NAND...? Return true if x and y are not true, except when they are, then return true...?
def encrypt(data, key, func):
length = len(key)
output = []
for i in range(len(data)):
output.append(func(data[i],key[i%length]))
print(output)
return bytes(output)
if __name__ == "__main__":
file_path = 'flag'
with open(file_path, 'rb') as file:
data = file.read()
key = []
for i in range(random.randrange(8192, 16384)):
key.append(random.randrange(0,255))
key = bytes(key)
rand = random.randrange(0, 8)
function = [Or, And, xor, nor, nand, xnor, xand, xnand]
print (base64.b64encode(encrypt(data, key, function[rand])).decode("utf-8"))
```
## Challenge Summary
In essence, we are able to connect to a server, which generates a random key of length ``[8192, 16384]`` bytes, and chooses a random bitwise operation (OR, AND, XOR, NOR, NAND, XNOR, XAND, XNAND) to apply on the contents of a file called ``flag`` (henceforth referred to as the plaintext). We are then provided the output (henceforth referred to as the ciphertext) in the form of an integer array and base-64 encoded string.
## Preliminary Analysis
From the code, one important observation to make is that the plaintext appears to contain binary data, as evident by the ``rb`` in ``with open(file_path, 'rb') as file:``, which stands for ``read binary`` mode.
This implies that the plaintext is unlikely to contain English sentences, meaning we cannot use cryptanalysis techniques such as [Kasiski Examination](https://en.wikipedia.org/wiki/Kasiski_examination) or [Index of Coincidence](https://en.wikipedia.org/wiki/Index_of_coincidence).
**Script**
```py
from pwn import *
r = remote("challenges1.whitehacks.xyz", 43232)
a = r.readline() #First line contains the output in the form of an array
print(a.count(b',') + 1)
```
**Output**
```
[x] Opening connection to challenges1.whitehacks.xyz on port 43232
[x] Opening connection to challenges1.whitehacks.xyz on port 43232: Trying 34.126.71.209
[+] Opening connection to challenges1.whitehacks.xyz on port 43232: Done
6231
```
Moreover, when we run the script above, it is evident that the length of the ciphertext (and thus plaintext) is smaller than the length of the random key, meaning that the random key essentially acts as a [One Time Pad](https://en.wikipedia.org/wiki/One-time_pad) which provides perfect secrecy assuming that the OTP is not re-used (which it isn't in this case).
Wait, doesn't that mean that there is nothing we can do?? Well...
## Statistical Analysis
Going back to the challenge author's hint, perhaps the key to solving the challenge first and foremost lies in being able to distinguish between each of the bitwise operations that can be randomly selected.
Using the following script, we can try and take the mean of all the ciphertext's byte values, to see if there is any pattern unique to each of the bitwise operations using a random plaintext as the input (in my case, I chose a random ``.jpg`` image file).
**Script**
```py
import os
import random
import base64
Not = lambda x: 255-x
Or = lambda x,y:x|y
And = lambda x,y:x&y
xor = lambda x,y:x^y
nor = lambda x,y:Not(x|y)
nand= lambda x,y:Not(x&y)
xnor = lambda x,y:Not(x^y)
xand = lambda x,y:Not(x&y)&(x&y) # Exclusive AND...? Returns true if x and y are true, except when they are, then retrun false...?
xnand = lambda x,y:Not(x&y)|(x&y) # Exclusive NAND...? Return true if x and y are not true, except when they are, then return true...?
def encrypt(data, key, func):
length = len(key)
output = []
for i in range(len(data)):
output.append(func(data[i],key[i%length]))
return output
def test(rand):
file_path = 'flag'
with open(file_path, 'rb') as file:
data = file.read()
key = []
for i in range(random.randrange(8192, 16384)):
key.append(random.randrange(0,255))
key = bytes(key)
function = [Or, And, xor, nor, nand, xnor, xand, xnand]
return encrypt(data, key, function[rand])
def stats():
for mode in range(8):
s = 0
l = 0
for repeat in range(100): #Take avg of 100 test() calls
res = test(mode)
for x in res:
s += x
l += len(res)
print(mode, s/l)
stats()
```
**Output**
```
0 184.75373799533799
1 57.36424522144522
2 127.39678508158508
3 70.26439254079254
4 197.6531393939394
5 127.65518974358974
6 0.0
7 255.0
```
Based on the output, we can somewhat distinguish between each of the bitwise operations based on their mean:
1. XAND always returns 0 (and XNAND always returns 255)
2. XOR and XNOR return approximately 127
3. Excluding XAND and XNAND, AND returns the lowest value (and NAND returns the highest value)
4. Excluding XAND and XNAND, OR returns the 2nd highest value (and NOR returns the 2nd lowest value)
Another observation that can be made is the mean values of the NOT versions of the bitwise operations are equivalent to ``255 - (mean value of the original bitwise operation)``, and vice versa (e.g. ``mean(AND) = 255 - mean(NAND)`` and ``mean(NAND) = 255 - mean(AND)``).
Note: It is possible to re-run the script above with different input files to see verify the correctness of the observations listed above.
## Now Which Bitwise Operation Leaks Information?
Now that we know how to somewhat distinguish between each of the bitwise operations, the next step is to choose which bitwise operation to focus on, and figure out how to leak information from it.
Out of the 8 bitwise operations, only 4 of them seem to useful (AND, NAND, OR, NOR), as XAND/XNAND always return a fixed value, while there is difficulty distinguishing between XOR/XNOR since their values are very similar.
After some thinking, it is evident that the AND operation should be chosen, as it is leaks information on the '1' bits of the plaintext's bytes.
Take the following example for a single plaintext byte and key byte:
```
pt = 0x83 = 0b10000011
key = 0x3e = 0b00111110
AND 0b00000010
```
This shows how when the AND operation is applied by the server, the presence of '1' bits in the plaintext's bytes can be leaked. Unlike the OR operation, which may introduce erroneous '1' bits in the result, due to the property of AND, it will only ever return a '1' bit in any position if there is a '1' bit at the same position in both the plaintext byte and key byte.
In order to extract the full plaintext byte, since the plaintext byte is constant (and only the key byte changes), we can just continuously query the server, and if the ciphertext is determined to be the result of AND (using the mean property mentioned earlier), simply OR it with previous ciphertexts that are determined to be the result of AND.
For instance, continuing off the previous example:
```
pt = 0x83 = 0b10000011
key = 0xa0 = 0b10100000
AND 0b10000000
pt = 0x83 = 0b10000011
key = 0x77 = 0b01110111
AND 0b00000011
Recovered pt = 0b00000010
0b10000000
0b00000011
OR 0b10000011
```
## Complete Script
While the general proof-of-concept of using the AND operation to leak the plaintext is feasible, unfortunately, there is some ambiguity in distinguishing between the AND and NOR bitwise operations as they share similar ciphertext mean values.
However, through trial and error, it was found that ``mean < 62.5`` should be sufficient to extract the plaintext from the server. In the event where this does not work (i.e. the script produces garbage, then just re-run the script).
**Script**
```py
from pwn import *
import ast
def avg(arr):
return sum(arr)/len(arr)
cpy = None
for rounds in range(1000):
r = remote("challenges1.whitehacks.xyz", 43232)
arr = ast.literal_eval(str(r.readline())[2:-3]) #Parse as an array
r.readline() #Ignore base-64 encoded string
mean = avg(arr)
print(mean)
if mean != 0 and mean < 62.5: #Exclude mean == 0 for optimization purposes
if cpy == None:
cpy = arr
else:
cpy = [cpy[i] | arr[i] for i in range(len(cpy))]
print(cpy)
```
**Output**
```
[118, 175, 177, 184, 242, 245, 229, 245, 255, 255, 255, 242, 182, 183, 187, 173, 255, 255, 254, 170, 255, 255, 255, 225, 247, 249, 255, 255, 255, 99, 27, 114, 202, 255, 255, 255, 251, 140, 189, 182, 171, 247, 247, 247, 247, 131, 247, 155, 119, 255, 255, 255, 230, 139, 186, 167, 139, 172, 144, 153, 139, 136, 158, 141, 154, 255, 152, 145, 144, 146, 154, 210, 140, 156, 141, 154, 154, 145, 140, 151, 144, 139, 16, 252, 64, 193, 255, 255, 255, 213, 139, 186, 167, 139, 188, 141, 154, 158, 139, 150, 144, 145, 223, 171, 150, 146, 154, 255, 172, 138, 145, 223, 207, 201, 223, 185, 154, 157, 223, 205, 207, 205, 205, 223, 206, 204, 197, 206, 205, 197, 203, 198, 223, 212, 207, 199, 189, 24, 116, 165, 255, 255, 232, 76, 182, 187, 190, 171, 135, 99, 18, 98, 132, 167, 107, 42, 69, 63, 128, 124, 111, 204, 247, 197, 124, 72, 230, 208, 246, 101, 196, 62, 179, 14, 237, 232, 74, 231, 203, 234, 43, 237, 74, 171, 47, 37, 95, 102, 93, 39, 14, 65, 218, 58, 235, 58, 171, 91, 108, 40, 13, 185, 196, 238, 180, 174, 52, 228, 133, 109, 116, 157, 127, 102, 117, 216, 12, 77, 178, 94, 108, 250, 107, 54, 79, 170, 103, 139, 155, 98, 192, 249, 143, 121, 102, 62, 254, 82, 66, 196, 24, 4, 194, 48, 8, 195, 49, 72, 65, 144, 82, 10, 81, 74, 33, 8, 164, 20, 162, 16, 189, 102, 239, 189, 223, 222, 222, 222, 222, 14, 167, 143, 7, 168, 168, 191, 189, 189, 189, 29, 0, 237, 109, 174, 106, 111, 111, 111, 135, 115, 183, 185, 170, 189, 189, 189, 29, 206, 221, 230, 170, 246, 246, 246, 118, 56, 119, 155, 171, 218, 219, 219, 219, 225, 220, 109, 174, 106, 111, 111, 111, 135, 115, 183, 185, 170, 189, 189, 189, 29, 206, 221, 230, 170, 246, 246, 246, 118, 56, 183, 74, 174, 210, 192, 195, 250, 114, 172, 132, 89, 90, 168, 43, 135, 91, 127, 74, 2, 164, 47, 95, 60, 243, 141, 242, 25, 24, 251, 59, 42, 42, 7, 196, 200, 29, 90, 114, 192, 221, 49, 210, 89, 4, 236, 145, 67, 73, 16, 65, 106, 157, 181, 38, 195, 91, 218, 114, 160, 163, 188, 174, 10, 194, 194, 40, 193, 164, 55, 119, 24, 97, 189, 90, 175, 95, 47, 135, 45, 192, 195, 97, 35, 228, 61, 19, 66, 19, 74, 108, 23, 24, 38, 245, 122, 84, 117, 169, 162, 125, 102, 2, 14, 72, 23, 178, 76, 201, 235, 108, 9, 17, 20, 7, 136, 147, 117, 189, 94, 63, 82, 92, 224, 156, 232, 224, 95, 55, 159, 13, 51, 114, 108, 83, 130, 140, 255, 161, 229, 152, 235, 245, 234, 226, 133, 242, 152, 9, 49, 229, 6, 175, 51, 62, 102, 254, 151, 163, 226, 143, 10, 114, 26, 29, 114, 48, 231, 32, 94, 246, 226, 56, 90, 95, 84, 214, 113, 209, 108, 214, 176, 212, 150, 196, 217, 54, 215, 112, 30, 231, 172, 37, 54, 142, 175, 249, 76, 222, 64, 153, 4, 190, 134, 181, 251, 49, 114, 189, 6, 19, 97, 26, 198, 116, 61, 50, 220, 175, 55, 155, 75, 226, 104, 173, 92, 193, 57, 201, 37, 193, 165, 124, 51, 182, 60, 148, 196, 144, 165, 91, 117, 224, 192, 91, 160, 28, 248, 130, 153, 19, 252, 248, 155, 205, 102, 14, 141, 173, 95, 45, 135, 45, 4, 90, 14, 59, 18, 3, 41, 173, 241, 196, 199, 12, 177, 144, 99, 100, 185, 111, 149, 165, 136, 34, 198, 73, 64, 2, 213, 1, 97, 82, 175, 214, 155, 55, 235, 213, 165, 138, 246, 155, 19, 29, 235, 13, 10, 10, 198, 180, 173, 53, 102, 91, 122, 123, 242, 23, 190, 4, 25, 49, 215, 235, 245, 203, 97, 129, 115, 99, 65, 105, 115, 224, 149, 115, 70, 181, 230, 162, 133, 57, 109, 152, 79, 211, 212, 18, 192, 97, 201, 230, 152, 106, 18, 168, 42, 225, 169, 209, 26, 231, 148, 18, 145, 118, 71, 67, 229, 128, 24, 249, 74, 25, 170, 90, 220, 40, 41, 241, 185, 158, 218, 162, 46, 67, 194, 66, 120, 48, 155, 56, 200, 154, 217, 198, 232, 76, 137, 175, 244, 229, 248, 146, 77, 37, 192, 29, 36, 234, 139, 136, 137, 25, 74, 194, 8, 50, 27, 72, 166, 240, 184, 144, 105, 130, 156, 198, 249, 82, 156, 90, 130, 99, 235, 87, 195, 67, 23, 224, 65, 123, 43, 131, 212, 130, 134, 4, 237, 68, 32, 98, 55, 31, 161, 226, 175, 70, 213, 175, 71, 85, 23, 47, 212, 103, 87, 234, 248, 146, 9, 130, 30, 104, 118, 51, 229, 42, 248, 80, 73, 145, 215, 235, 245, 171, 146, 66, 23, 224, 5, 201, 164, 176, 102, 112, 22, 37, 146, 119, 22, 204, 138, 104, 64, 169, 194, 84, 124, 1, 117, 208, 92, 150, 16, 27, 127, 36, 172, 62, 211, 52, 77, 43, 182, 255, 56, 85, 128, 215, 3, 161, 63, 80, 14, 56, 27, 155, 99, 122, 63, 225, 240, 97, 215, 2, 117, 11, 76, 218, 171, 35, 54, 223, 28, 93, 63, 72, 116, 83, 197, 182, 104, 138, 115, 76, 234, 48, 237, 40, 168, 252, 136, 146, 73, 124, 170, 181, 241, 51, 95, 0, 103, 226, 151, 1, 69, 103, 18, 52, 132, 221, 208, 177, 154, 170, 11, 195, 121, 113, 148, 55, 86, 43, 215, 35, 126, 148, 100, 60, 230, 195, 16, 221, 124, 232, 146, 219, 34, 64, 214, 192, 154, 1, 216, 76, 32, 227, 181, 86, 13, 148, 201, 65, 27, 249, 23, 54, 129, 196, 123, 222, 224, 105, 204, 221, 133, 220, 180, 3, 170, 107, 27, 129, 55, 125, 103, 168, 134, 58, 206, 116, 83, 23, 225, 159, 71, 179, 3, 87, 239, 157, 65, 8, 154, 129, 61, 129, 75, 146, 16, 141, 133, 36, 196, 211, 135, 130, 219, 77, 153, 88, 166, 238, 23, 243, 127, 199, 8, 222, 244, 201, 163, 89, 176, 3, 200, 83, 134, 82, 204, 149, 232, 119, 160, 234, 185, 112, 206, 140, 103, 12, 181, 159, 154, 134, 255, 133, 45, 157, 152, 109, 135, 216, 111, 210, 212, 61, 175, 100, 55, 219, 17, 91, 237, 232, 76, 120, 206, 36, 185, 93, 75, 84, 234, 245, 39, 1, 54, 142, 203, 194, 66, 46, 90, 217, 12, 38, 208, 220, 231, 34, 163, 153, 26, 70, 221, 73, 56, 211, 222, 195, 151, 234, 165, 168, 148, 22, 89, 55, 230, 77, 139, 224, 44, 2, 115, 32, 180, 130, 46, 218, 77, 240, 216, 77, 217, 83, 216, 54, 4, 168, 108, 109, 199, 126, 177, 113, 240, 52, 92, 233, 243, 104, 166, 196, 197, 103, 198, 32, 138, 154, 25, 36, 100, 167, 26, 34, 245, 70, 190, 56, 58, 92, 118, 211, 118, 132, 106, 254, 168, 137, 141, 53, 145, 6, 254, 188, 254, 36, 56, 240, 156, 61, 49, 157, 69, 112, 97, 61, 36, 144, 59, 93, 142, 46, 172, 135, 193, 108, 27, 178, 128, 92, 32, 113, 194, 83, 37, 128, 127, 22, 66, 99, 50, 161, 68, 140, 209, 126, 103, 114, 94, 19, 116, 19, 15, 47, 221, 227, 197, 184, 79, 22, 66, 207, 35, 226, 210, 44, 155, 50, 66, 110, 36, 174, 178, 166, 68, 174, 83, 196, 7, 243, 218, 106, 64, 52, 204, 168, 207, 141, 150, 206, 236, 73, 57, 236, 45, 73, 77, 194, 234, 17, 139, 141, 107, 142, 236, 95, 94, 208, 76, 137, 209, 222, 55, 91, 64, 11, 40, 176, 109, 11, 161, 253, 158, 208, 25, 92, 48, 182, 222, 35, 92, 65, 244, 186, 198, 2, 104, 17, 155, 97, 96, 76, 106, 203, 234, 225, 225, 138, 20, 160, 120, 49, 108, 38, 73, 153, 155, 26, 167, 41, 92, 68, 107, 54, 69, 154, 16, 15, 53, 38, 205, 177, 131, 66, 107, 145, 170, 28, 90, 7, 247, 172, 121, 113, 156, 188, 129, 148, 121, 176, 103, 49, 69, 103, 9, 215, 214, 218, 0, 59, 225, 41, 210, 228, 181, 13, 97, 64, 110, 109, 69, 235, 82, 85, 85, 131, 194, 232, 41, 121, 205, 155, 133, 213, 77, 127, 247, 221, 232, 176, 56, 172, 82, 191, 128, 194, 112, 124, 36, 201, 207, 26, 6, 155, 173, 40, 226, 154, 168, 59, 60, 4, 15, 46, 27, 72, 176, 48, 19, 46, 160, 166, 16, 231, 49, 27, 64, 59, 37, 40, 120, 79, 147, 14, 137, 61, 64, 119, 205, 76, 254, 57, 115, 85, 214, 237, 148, 249, 201, 232, 81, 254, 84, 186, 1, 124, 100, 93, 211, 202, 173, 87, 36, 151, 186, 79, 144, 204, 14, 29, 69, 20, 217, 214, 26, 29, 63, 7, 88, 187, 92, 49, 12, 59, 38, 132, 234, 93, 221, 144, 110, 15, 137, 173, 118, 142, 96, 228, 123, 218, 197, 78, 150, 143, 244, 30, 37, 128, 74, 215, 83, 211, 52, 3, 72, 110, 100, 118, 60, 122, 67, 94, 169, 83, 0, 96, 4, 189, 35, 52, 234, 204, 67, 107, 93, 52, 83, 236, 93, 35, 219, 96, 107, 40, 196, 247, 104, 127, 234, 57, 197, 33, 1, 179, 115, 150, 30, 213, 133, 210, 5, 57, 77, 161, 48, 209, 201, 41, 212, 156, 69, 15, 111, 132, 119, 87, 75, 196, 240, 225, 86, 51, 68, 28, 43, 208, 85, 144, 170, 91, 185, 245, 90, 140, 119, 39, 142, 76, 61, 83, 33, 248, 57, 132, 246, 24, 241, 238, 29, 175, 26, 2, 77, 35, 136, 123, 72, 189, 210, 161, 6, 4, 112, 217, 6, 154, 117, 55, 216, 100, 119, 129, 30, 94, 61, 188, 33, 182, 51, 201, 210, 180, 247, 174, 73, 212, 163, 215, 99, 56, 119, 66, 136, 212, 51, 17, 168, 99, 160, 209, 67, 162, 195, 58, 3, 11, 34, 157, 179, 84, 89, 157, 23, 105, 224, 122, 198, 26, 221, 150, 107, 165, 75, 245, 118, 239, 222, 229, 232, 46, 152, 22, 134, 12, 8, 80, 128, 223, 253, 162, 194, 187, 171, 37, 130, 28, 16, 165, 5, 31, 88, 162, 108, 123, 88, 189, 222, 5, 211, 2, 37, 221, 82, 201, 177, 208, 11, 232, 245, 72, 143, 142, 87, 77, 17, 234, 24, 104, 244, 144, 122, 165, 67, 14, 6, 226, 116, 152, 80, 81, 230, 210, 69, 8, 97, 174, 34, 169, 9, 143, 138, 178, 79, 175, 197, 69, 116, 78, 128, 0, 49, 205, 14, 185, 121, 119, 19, 45, 187, 203, 21, 197, 176, 27, 107, 168, 105, 96, 72, 183, 135, 68, 7, 117, 47, 142, 194, 123, 93, 10, 231, 78, 24, 152, 12, 77, 113, 65, 10, 232, 108, 142, 154, 147, 192, 232, 96, 58, 29, 93, 34, 202, 77, 112, 77, 226, 94, 189, 33, 47, 168, 219, 3, 28, 65, 170, 102, 235, 176, 251, 118, 82, 192, 164, 73, 188, 186, 62, 248, 221, 47, 42, 166, 11, 85, 17, 52, 181, 66, 228, 75, 174, 107, 167, 214, 56, 39, 33, 245, 206, 145, 72, 78, 176, 148, 40, 76, 69, 157, 68, 130, 115, 69, 23, 212, 29, 209, 171, 54, 168, 219, 109, 185, 74, 232, 77, 89, 190, 221, 30, 64, 210, 4, 65, 211, 8, 162, 30, 24, 21, 223, 97, 101, 79, 64, 165, 113, 117, 80, 32, 238, 33, 245, 122, 135, 153, 45, 129, 204, 194, 232, 189, 247, 142, 208, 160, 219, 66, 25, 214, 155, 114, 75, 221, 30, 61, 60, 56, 144, 234, 10, 110, 0, 94, 133, 169, 240, 2, 66, 229, 224, 215, 229, 138, 202, 37, 65, 101, 103, 131, 213, 164, 237, 231, 47, 250, 60, 168, 230, 27, 105, 195, 103, 57, 96, 50, 195, 182, 166, 72, 206, 187, 195, 40, 125, 67, 83, 115, 248, 180, 235, 60, 198, 45, 76, 145, 31, 41, 200, 79, 225, 204, 96, 105, 115, 34, 131, 109, 140, 118, 236, 51, 83, 67, 77, 102, 229, 198, 26, 23, 10, 223, 81, 225, 220, 216, 160, 186, 191, 111, 96, 54, 179, 93, 246, 126, 124, 131, 71, 128, 213, 124, 115, 160, 251, 203, 229, 55, 5, 108, 160, 78, 144, 165, 152, 108, 163, 27, 87, 101, 202, 190, 3, 169, 125, 225, 111, 6, 57, 111, 137, 201, 114, 58, 48, 100, 131, 42, 227, 164, 93, 150, 25, 183, 22, 146, 52, 122, 96, 35, 147, 37, 45, 123, 62, 52, 236, 231, 210, 173, 135, 212, 197, 242, 98, 193, 112, 170, 44, 169, 12, 12, 63, 106, 83, 129, 82, 106, 58, 68, 85, 193, 46, 59, 65, 131, 104, 242, 46, 84, 71, 155, 154, 150, 165, 108, 76, 196, 137, 14, 112, 9, 156, 231, 46, 200, 103, 79, 223, 234, 102, 196, 137, 100, 71, 184, 225, 159, 151, 237, 61, 109, 198, 130, 198, 96, 207, 100, 187, 212, 52, 236, 132, 47, 115, 131, 104, 39, 168, 164, 110, 66, 145, 244, 230, 26, 112, 15, 24, 225, 145, 20, 47, 244, 47, 164, 110, 80, 2, 43, 226, 99, 193, 78, 117, 223, 106, 98, 28, 62, 143, 113, 210, 100, 113, 142, 64, 128, 203, 212, 160, 76, 205, 164, 150, 229, 191, 131, 163, 215, 81, 32, 217, 77, 10, 64, 53, 50, 109, 133, 179, 164, 179, 135, 92, 188, 59, 59, 90, 38, 74, 131, 0, 136, 190, 41, 69, 228, 34, 203, 125, 93, 224, 245, 0, 42, 170, 86, 226, 56, 121, 127, 253, 90, 116, 14, 88, 71, 5, 214, 20, 9, 234, 46, 132, 57, 181, 89, 136, 78, 99, 222, 213, 131, 33, 221, 193, 45, 100, 84, 54, 20, 38, 164, 215, 255, 194, 120, 201, 218, 110, 40, 135, 231, 116, 28, 249, 164, 49, 25, 227, 34, 246, 164, 206, 104, 190, 242, 112, 108, 71, 202, 24, 136, 234, 58, 161, 194, 84, 108, 1, 201, 107, 124, 62, 133, 109, 38, 5, 60, 172, 4, 195, 17, 234, 198, 91, 152, 170, 242, 31, 253, 77, 140, 65, 24, 166, 192, 128, 253, 4, 5, 159, 199, 97, 50, 38, 181, 122, 235, 168, 112, 110, 12, 124, 115, 255, 82, 96, 38, 13, 182, 35, 209, 186, 88, 44, 42, 71, 181, 211, 107, 175, 81, 137, 56, 92, 114, 61, 27, 113, 97, 11, 115, 163, 17, 73, 9, 60, 48, 188, 249, 6, 32, 140, 78, 61, 226, 240, 240, 12, 245, 212, 36, 73, 188, 130, 192, 96, 3, 253, 254, 55, 174, 69, 136, 189, 82, 203, 174, 157, 60, 154, 45, 76, 245, 143, 20, 26, 144, 203, 9, 141, 218, 225, 98, 195, 175, 101, 211, 2, 59, 112, 56, 183, 0, 89, 253, 224, 192, 16, 37, 228, 241, 95, 22, 191, 29, 32, 240, 60, 15, 46, 187, 61, 189, 56, 236, 8, 2, 244, 59, 81, 241, 74, 227, 219, 63, 144, 87, 246, 162, 11, 233, 48, 2, 28, 192, 102, 76, 10, 165, 18, 6, 229, 177, 77, 130, 40, 136, 135, 120, 242, 88, 100, 92, 99, 63, 78, 188, 150, 105, 100, 51, 113, 212, 41, 114, 89, 40, 91, 122, 187, 73, 52, 218, 217, 153, 176, 66, 131, 92, 47, 123, 31, 222, 193, 203, 1, 202, 120, 115, 180, 10, 200, 85, 77, 81, 252, 46, 193, 86, 220, 150, 37, 175, 153, 144, 178, 28, 29, 114, 5, 24, 218, 129, 195, 185, 17, 136, 253, 32, 94, 62, 169, 36, 236, 191, 94, 226, 119, 73, 14, 80, 155, 153, 98, 202, 80, 184, 92, 190, 51, 160, 239, 51, 114, 178, 244, 135, 48, 241, 224, 93, 161, 80, 72, 67, 147, 215, 58, 16, 181, 22, 8, 27, 32, 151, 127, 165, 156, 180, 157, 196, 78, 217, 112, 161, 144, 172, 46, 224, 117, 190, 231, 32, 202, 23, 214, 197, 2, 246, 76, 237, 241, 46, 25, 106, 183, 189, 37, 229, 178, 123, 209, 216, 104, 76, 136, 0, 189, 143, 111, 88, 114, 243, 27, 7, 242, 229, 127, 4, 34, 227, 205, 177, 106, 124, 30, 205, 38, 198, 122, 203, 44, 241, 72, 2, 110, 146, 198, 119, 30, 129, 178, 54, 48, 53, 25, 173, 162, 20, 148, 80, 3, 138, 47, 76, 197, 22, 144, 210, 103, 230, 170, 166, 40, 255, 75, 210, 53, 224, 243, 31, 160, 112, 110, 97, 40, 231, 64, 65, 97, 215, 2, 131, 15, 65, 106, 182, 57, 134, 92, 237, 234, 154, 98, 219, 48, 62, 232, 146, 160, 44, 80, 105, 113, 91, 79, 89, 87, 171, 85, 229, 104, 248, 174, 184, 129, 86, 74, 221, 218, 120, 92, 118, 37, 7, 236, 124, 232, 49, 61, 40, 174, 121, 161, 88, 28, 200, 222, 184, 22, 173, 92, 188, 107, 181, 107, 205, 226, 69, 164, 41, 141, 46, 108, 226, 196, 118, 170, 104, 96, 154, 185, 11, 143, 20, 129, 238, 2, 218, 41, 178, 131, 120, 28, 18, 32, 219, 37, 155, 73, 86, 40, 104, 220, 76, 30, 162, 172, 242, 166, 57, 53, 174, 241, 227, 37, 132, 126, 193, 46, 212, 246, 144, 148, 36, 232, 217, 132, 133, 221, 78, 108, 194, 183, 116, 116, 156, 16, 208, 73, 242, 177, 6, 46, 112, 38, 4, 92, 200, 94, 80, 231, 248, 86, 93, 48, 215, 189, 97, 67, 59, 113, 162, 232, 82, 64, 223, 8, 158, 41, 93, 46, 199, 90, 211, 223, 209, 84, 51, 5, 204, 240, 190, 81, 150, 120, 21, 129, 238, 58, 74, 136, 58, 188, 205, 134, 126, 7, 194, 224, 206, 70, 2, 234, 41, 113, 16, 112, 104, 57, 102, 169, 33, 126, 115, 98, 238, 48, 33, 76, 218, 240, 128, 32, 107, 93, 221, 245, 16, 194, 126, 184, 100, 165, 243, 179, 188, 136, 195, 37, 195, 62, 48, 40, 244, 210, 153, 91, 101, 46, 244, 102, 38, 28, 196, 237, 93, 72, 167, 98, 134, 171, 142, 4, 155, 243, 33, 245, 250, 117, 101, 104, 35, 108, 103, 172, 10, 100, 6, 36, 122, 62, 11, 45, 92, 212, 55, 219, 193, 205, 121, 60, 8, 132, 238, 193, 57, 20, 238, 205, 41, 78, 146, 107, 116, 90, 195, 245, 250, 178, 161, 182, 85, 12, 184, 8, 9, 54, 231, 195, 98, 227, 111, 198, 230, 200, 85, 203, 194, 60, 198, 35, 139, 217, 228, 236, 185, 171, 128, 19, 181, 117, 116, 110, 202, 47, 95, 145, 172, 52, 213, 59, 188, 114, 37, 22, 209, 186, 186, 218, 191, 238, 186, 186, 8, 175, 73, 46, 43, 29, 76, 145, 118, 89, 178, 156, 53, 117, 13, 214, 75, 77, 118, 148, 228, 4, 26, 80, 84, 97, 38, 84, 64, 245, 184, 230, 61, 95, 72, 69, 181, 205, 72, 241, 141, 224, 253, 4, 201, 94, 207, 212, 98, 180, 191, 134, 49, 206, 49, 197, 6, 31, 32, 178, 121, 83, 90, 208, 37, 113, 58, 155, 155, 162, 252, 11, 155, 96, 7, 101, 249, 34, 75, 151, 202, 89, 114, 211, 152, 55, 45, 208, 183, 180, 176, 84, 142, 18, 158, 121, 96, 53, 153, 250, 244, 240, 179, 88, 160, 23, 184, 203, 2, 112, 235, 201, 165, 166, 169, 36, 184, 214, 150, 244, 120, 206, 221, 190, 56, 71, 82, 182, 179, 8, 75, 157, 7, 145, 96, 156, 18, 87, 158, 51, 66, 19, 56, 89, 226, 180, 15, 106, 168, 41, 162, 160, 63, 97, 162, 70, 199, 195, 24, 178, 200, 122, 106, 190, 172, 101, 180, 133, 49, 242, 27, 209, 143, 153, 0, 222, 245, 149, 98, 242, 55, 14, 96, 76, 107, 46, 242, 173, 167, 71, 221, 36, 57, 45, 75, 107, 188, 96, 227, 30, 169, 32, 206, 57, 102, 127, 254, 95, 212, 158, 80, 135, 142, 222, 134, 68, 42, 162, 146, 255, 42, 111, 122, 187, 240, 67, 58, 121, 134, 20, 19, 141, 208, 39, 93, 158, 66, 32, 203, 93, 23, 195, 117, 138, 56, 128, 95, 15, 100, 139, 73, 80, 103, 186, 79, 56, 144, 155, 216, 49, 158, 7, 140, 18, 22, 202, 2, 191, 82, 249, 49, 243, 184, 156, 178, 53, 148, 130, 183, 240, 249, 126, 51, 53, 217, 236, 113, 176, 204, 218, 17, 242, 101, 224, 162, 185, 51, 193, 20, 196, 78, 159, 35, 119, 38, 98, 108, 178, 137, 50, 212, 136, 240, 110, 162, 129, 96, 87, 189, 142, 200, 106, 119, 169, 170, 121, 85, 149, 168, 162, 180, 35, 72, 161, 51, 32, 102, 59, 27, 113, 112, 173, 81, 99, 222, 52, 176, 167, 53, 108, 108, 178, 25, 53, 62, 9, 144, 237, 169, 29, 47, 134, 205, 132, 177, 98, 30, 51, 86, 204, 99, 198, 106, 178, 9, 94, 138, 3, 74, 14, 209, 185, 11, 229, 62, 41, 85, 230, 162, 252, 196, 205, 205, 171, 42, 49, 13, 97, 18, 136, 17, 126, 111, 156, 178, 18, 147, 156, 80, 3, 10, 46, 204, 132, 11, 232, 43, 33, 48, 45, 17, 56, 243, 109, 44, 210, 34, 199, 202, 121, 85, 227, 0, 127, 97, 35, 0, 211, 120, 99, 189, 62, 50, 51, 80, 70, 44, 212, 245, 160, 168, 230, 47, 234, 64, 65, 82, 135, 192, 212, 232, 34, 75, 113, 155, 152, 2, 236, 112, 47, 191, 35, 148, 67, 80, 133, 185, 180, 95, 73, 153, 240, 107, 141, 50, 50, 246, 129, 84, 166, 67, 97, 244, 224, 178, 157, 155, 43, 238, 197, 211, 39, 48, 73, 198, 66, 84, 228, 187, 81, 171, 45, 175, 169, 119, 17, 73, 255, 44, 98, 197, 98, 241, 98, 175, 93, 139, 202, 54, 57, 175, 51, 17, 72, 161, 153, 61, 88, 205, 93, 137, 224, 155, 14, 255, 212, 121, 6, 40, 179, 33, 241, 230, 50, 248, 0, 227, 179, 45, 232, 100, 246, 86, 37, 222, 203, 227, 158, 131, 68, 104, 7, 59, 138, 251, 100, 64, 103, 166, 188, 225, 156, 34, 240, 49, 98, 54, 32, 98, 221, 199, 7, 186, 164, 25, 240, 167, 55, 75, 114, 62, 74, 16, 197, 200, 230, 55, 109, 250, 2, 14, 101, 197, 116, 242, 238, 160, 205, 54, 93, 209, 184, 39, 65, 0, 132, 145, 35, 99, 119, 57, 150, 93, 134, 165, 124, 100, 219, 24, 211, 94, 164, 160, 148, 92, 83, 218, 28, 104, 49, 153, 84, 32, 221, 25, 131, 227, 57, 24, 252, 146, 168, 62, 229, 69, 212, 104, 214, 147, 159, 22, 173, 86, 208, 53, 152, 75, 123, 193, 92, 218, 139, 133, 211, 35, 209, 159, 8, 35, 46, 115, 162, 228, 186, 61, 47, 159, 169, 251, 37, 158, 203, 43, 149, 203, 177, 136, 214, 5, 209, 224, 135, 53, 5, 204, 64, 234, 110, 160, 139, 112, 73, 146, 35, 110, 252, 202, 42, 191, 46, 132, 209, 212, 60, 193, 152, 171, 11, 237, 221, 249, 83, 77, 101, 122, 76, 116, 249, 208, 160, 192, 197, 42, 186, 71, 184, 90, 94, 208, 12, 8, 82, 156, 71, 100, 78, 224, 52, 140, 104, 204, 157, 9, 198, 57, 146, 183, 221, 69, 80, 74, 162, 148, 149, 14, 242, 40, 99, 20, 54, 174, 138, 13, 58, 48, 40, 225, 180, 8, 143, 99, 162, 203, 135, 9, 11, 201, 150, 224, 192, 3, 161, 19, 254, 193, 165, 233, 209, 33, 188, 23, 73, 110, 151, 37, 75, 92, 158, 186, 113, 46, 18, 153, 202, 189, 250, 7, 94, 127, 93, 132, 114, 22, 45, 185, 242, 35, 63, 92, 114, 244, 214, 250, 6, 23, 23, 146, 60, 47, 232, 108, 128, 66, 243, 24, 73, 229, 43, 138, 37, 104, 78, 172, 1, 5, 21, 38, 60, 11, 232, 111, 6, 59, 111, 235, 100, 56, 31, 62, 226, 55, 99, 138, 107, 0, 161, 41, 68, 197, 50, 157, 27, 84, 74, 208, 47, 82, 221, 104, 99, 99, 204, 155, 96, 213, 91, 148, 160, 0, 21, 218, 127, 128, 96, 161, 35, 0, 213, 100, 19, 12, 230, 155, 235, 85, 247, 47, 37, 30, 108, 83, 122, 61, 107, 54, 243, 118, 197, 177, 112, 8, 112, 77, 148, 177, 114, 121, 16, 7, 203, 97, 241, 104, 55, 64, 157, 1, 113, 17, 53, 154, 117, 227, 195, 14, 133, 85, 85, 206, 181, 182, 100, 196, 115, 142, 96, 68, 238, 108, 101, 153, 34, 95, 33, 193, 56, 109, 168, 56, 15, 190, 186, 251, 214, 89, 249, 234, 63, 14, 250, 105, 225, 6, 107, 182, 82, 45, 102, 194, 60, 141, 230, 166, 141, 135, 225, 174, 128, 64, 176, 187, 61, 131, 253, 130, 216, 76, 137, 113, 216, 184, 156, 93, 225, 69, 158, 91, 230, 228, 56, 51, 81, 168, 119, 116, 33, 189, 158, 242, 172, 175, 71, 8, 172, 241, 52, 121, 77, 209, 20, 139, 26, 19, 95, 21, 197, 187, 11, 140, 192, 12, 166, 141, 69, 178, 250, 108, 138, 129, 108, 7, 118, 18, 182, 164, 67, 127, 43, 109, 245, 229, 53, 19, 226, 115, 58, 19, 1, 19, 219, 8, 97, 45, 93, 82, 156, 55, 114, 230, 121, 173, 13, 80, 164, 166, 159, 69, 71, 204, 221, 153, 205, 37, 216, 129, 222, 16, 109, 130, 100, 207, 77, 105, 254, 151, 96, 110, 108, 68, 192, 106, 253, 228, 48, 107, 152, 227, 222, 28, 96, 146, 247, 47, 37, 165, 209, 200, 222, 135, 46, 227, 97, 0, 134, 220, 76, 168, 96, 126, 249, 176, 39, 170, 9, 16, 114, 179, 87, 151, 16, 18, 114, 136, 176, 28, 26, 192, 10, 162, 157, 4, 34, 157, 130, 43, 237, 13, 51, 29, 198, 100, 95, 150, 25, 187, 166, 158, 193, 186, 169, 153, 177, 5, 3, 253, 245, 16, 74, 187, 82, 134, 123, 193, 84, 240, 113, 176, 28, 42, 78, 222, 69, 212, 6, 235, 255, 141, 192, 224, 69, 196, 160, 222, 138, 32, 166, 100, 80, 27, 227, 193, 177, 190, 236, 192, 75, 66, 227, 63, 46, 199, 246, 68, 106, 74, 120, 60, 73, 105, 46, 58, 120, 198, 139, 85, 243, 240, 146, 50, 54, 38, 28, 30, 174, 11, 83, 201, 2, 250, 239, 32, 129, 55, 43, 58, 104, 23, 76, 139, 192, 96, 49, 19, 145, 105, 153, 158, 171, 154, 18, 161, 191, 36, 238, 49, 155, 217, 108, 130, 65, 250, 129, 130, 224, 199, 89, 26, 129, 193, 135, 32, 53, 218, 194, 6, 180, 209, 214, 131, 246, 19, 170, 0, 113, 233, 24, 169, 207, 157, 29, 238, 97, 166, 65, 96, 146, 238, 98, 210, 65, 58, 57, 133, 23, 198, 99, 149, 213, 135, 206, 120, 241, 131, 122, 28, 12, 165, 253, 213, 98, 32, 40, 201, 120, 204, 137, 244, 211, 39, 100, 157, 238, 52, 151, 91, 107, 34, 144, 122, 77, 83, 199, 123, 107, 66, 180, 46, 165, 131, 154, 26, 87, 68, 242, 156, 54, 75, 159, 145, 1, 168, 249, 70, 89, 196, 28, 64, 225, 158, 41, 75, 18, 203, 231, 68, 109, 58, 252, 35, 255, 198, 34, 152, 218, 207, 6, 54, 227, 233, 167, 206, 63, 153, 199, 193, 50, 51, 90, 144, 47, 3, 15, 205, 233, 91, 32, 205, 110, 48, 231, 204, 24, 237, 235, 181, 187, 96, 17, 42, 181, 152, 67, 125, 231, 0, 149, 200, 81, 16, 182, 217, 28, 105, 82, 26, 66, 227, 0, 134, 244, 135, 70, 157, 232, 140, 169, 96, 24, 200, 196, 0, 28, 121, 148, 182, 44, 118, 196, 135, 120, 31, 55, 14, 240, 29, 241, 20, 115, 97, 124, 172, 132, 45, 62, 200, 45, 85, 64, 86, 67, 31, 205, 250, 234, 81, 71, 72, 78, 18, 21, 206, 60, 14, 150, 57, 64, 238, 191, 124, 236, 142, 51, 33, 135, 42, 205, 2, 40, 179, 25, 56, 19, 31, 137, 112, 143, 221, 252, 234, 105, 22, 106, 55, 165, 64, 177, 3, 243, 224, 177, 80, 167, 63, 33, 160, 1, 159, 28, 156, 200, 17, 115, 160, 193, 114, 152, 80, 66, 176, 171, 61, 230, 108, 4, 141, 3, 252, 131, 142, 2, 137, 208, 54, 56, 148, 199, 189, 243, 250, 147, 32, 67, 112, 96, 96, 243, 221, 87, 36, 224, 211, 104, 1, 227, 152, 209, 105, 93, 151, 84, 190, 242, 55, 165, 112, 217, 205, 59, 98, 44, 148, 153, 76, 19, 107, 90, 176, 64, 3, 11, 141, 153, 146, 67, 183, 24, 142, 110, 243, 84, 43, 78, 63, 200, 57, 30, 132, 8, 140, 233, 51, 78, 77, 36, 145, 215, 153, 8, 35, 234, 227, 105, 194, 48, 11, 119, 184, 100, 99, 166, 24, 238, 10, 51, 89, 1, 229, 214, 53, 5, 125, 140, 85, 158, 51, 99, 46, 240, 48, 153, 25, 156, 44, 45, 172, 26, 39, 106, 191, 146, 148, 237, 73, 144, 26, 101, 156, 247, 144, 11, 131, 47, 102, 185, 64, 149, 203, 84, 237, 12, 142, 13, 160, 190, 63, 188, 252, 46, 146, 174, 51, 105, 122, 84, 198, 40, 149, 231, 100, 195, 116, 182, 48, 215, 201, 182, 172, 95, 22, 29, 116, 152, 76, 81, 179, 98, 194, 119, 82, 108, 92, 103, 47, 137, 218, 172, 3, 98, 70, 73, 128, 198, 76, 241, 69, 207, 22, 31, 135, 28, 19, 70, 11, 247, 180, 156, 240, 45, 215, 215, 225, 96, 36, 70, 91, 152, 103, 155, 28, 91, 61, 52, 40, 100, 217, 88, 104, 76, 159, 56, 176, 251, 49, 240, 185, 99, 48, 223, 34, 75, 219, 168, 136, 67, 132, 73, 184, 241, 55, 162, 235, 203, 203, 140, 142, 104, 141, 143, 17, 243, 193, 70, 196, 109, 91, 199, 236, 192, 114, 35, 120, 218, 246, 30, 91, 249, 58, 207, 18, 28, 62, 19, 83, 58, 248, 83, 247, 7, 228, 78, 92, 137, 206, 205, 14, 223, 205, 120, 239, 255, 59, 72, 196, 182, 49, 65, 48, 95, 91, 223, 84, 241, 131, 112, 94, 208, 44, 210, 5, 226, 137, 91, 57, 236, 11, 85, 10, 154, 221, 178, 160, 153, 182, 179, 128, 133, 187, 146, 26, 85, 190, 178, 152, 76, 187, 194, 218, 24, 204, 183, 136, 82, 243, 1, 64, 142, 118, 19, 252, 118, 147, 182, 193, 176, 44, 46, 100, 167, 146, 184, 79, 67, 146, 27, 251, 176, 96, 58, 95, 130, 172, 230, 80, 122, 204, 204, 60, 47, 133, 73, 189, 154, 215, 222, 0, 19, 158, 41, 66, 72, 97, 29, 81, 140, 118, 227, 159, 36, 255, 41, 187, 204, 158, 194, 100, 140, 249, 206, 137, 181, 224, 133, 152, 178, 222, 29, 90, 17, 42, 62, 0, 132, 201, 218, 109, 142, 8, 186, 41, 89, 65, 2, 47, 79, 194, 80, 86, 244, 103, 67, 210, 103, 10, 68, 251, 177, 130, 51, 44, 53, 139, 250, 155, 88, 89, 14, 108, 74, 195, 227, 42, 139, 40, 133, 42, 38, 240, 166, 224, 155, 98, 88, 238, 224, 70, 108, 1, 212, 153, 12, 161, 55, 46, 149, 64, 64, 153, 147, 243, 204, 136, 243, 221, 25, 42, 129, 107, 51, 103, 181, 111, 72, 249, 70, 209, 112, 75, 112, 193, 159, 2, 142, 168, 57, 128, 197, 244, 82, 102, 44, 174, 176, 158, 161, 213, 22, 245, 20, 28, 60, 70, 92, 224, 65, 17, 9, 8, 190, 38, 18, 189, 49, 155, 91, 12, 172, 42, 242, 162, 254, 150, 182, 52, 166, 0, 112, 137, 187, 66, 168, 74, 30, 36, 123, 238, 84, 201, 204, 2, 61, 215, 93, 248, 11, 31, 11, 91, 214, 243, 8, 200, 246, 1, 32, 71, 100, 45, 97, 116, 199, 231, 36, 80, 133, 163, 52, 197, 48, 158, 12, 117, 76, 11, 116, 229, 184, 112, 125, 171, 89, 67, 233, 179, 200, 74, 253, 130, 174, 225, 248, 236, 200, 111, 131, 41, 122, 246, 164, 201, 40, 199, 251, 158, 188, 201, 122, 196, 1, 130, 37, 168, 17, 248, 195, 163, 129, 96, 196, 138, 47, 76, 30, 41, 36, 58, 101, 1, 169, 174, 145, 239, 55, 235, 141, 20, 100, 143, 41, 125, 154, 52, 9, 121, 244, 218, 119, 57, 188, 211, 252, 109, 112, 65, 10, 115, 255, 70, 135, 14, 130, 12, 159, 18, 197, 250, 0, 32, 52, 235, 110, 176, 201, 235, 231, 162, 155, 202, 209, 70, 231, 8, 22, 18, 21, 8, 177, 144, 101, 217, 253, 196, 70, 246, 70, 163, 214, 203, 162, 188, 59, 3, 34, 32, 170, 224, 249, 207, 105, 214, 76, 101, 112, 83, 13, 239, 62, 42, 202, 62, 189, 145, 74, 227, 187, 124, 53, 252, 253, 189, 195, 247, 1, 32, 164, 153, 3, 130, 140, 0, 155, 30, 222, 168, 116, 78, 96, 41, 243, 55, 200, 41, 20, 63, 100, 98, 122, 93, 10, 231, 110, 3, 172, 186, 138, 15, 15, 47, 210, 200, 211, 97, 83, 215, 7, 191, 251, 70, 202, 239, 77, 53, 31, 30, 44, 144, 8, 235, 245, 72, 206, 157, 16, 192, 146, 250, 55, 24, 116, 106, 48, 200, 236, 50, 121, 146, 236, 218, 106, 62, 38, 210, 1, 69, 32, 13, 78, 132, 134, 221, 9, 198, 200, 126, 92, 132, 114, 31, 0, 229, 18, 30, 93, 233, 161, 130, 189, 59, 83, 210, 160, 164, 242, 209, 128, 231, 202, 124, 0, 122, 239, 93, 3, 68, 171, 78, 155, 29, 239, 30, 2, 107, 181, 55, 226, 238, 71, 215, 122, 184, 200, 82, 247, 100, 96, 219, 209, 33, 77, 192, 15, 0, 254, 197, 142, 133, 164, 115, 247, 42, 137, 233, 149, 90, 163, 31, 215, 232, 21, 177, 65, 157, 59, 83, 178, 221, 24, 104, 229, 248, 217, 213, 124, 0, 236, 209, 167, 249, 34, 32, 35, 234, 209, 43, 113, 167, 251, 0, 164, 224, 152, 106, 28, 91, 78, 26, 94, 243, 132, 87, 144, 15, 64, 47, 226, 233, 238, 226, 228, 117, 153, 124, 51, 240, 38, 119, 164, 232, 186, 173, 11, 167, 30, 40, 182, 220, 27, 113, 247, 134, 204, 240, 46, 130, 151, 91, 167, 136, 3, 168, 180, 6, 146, 115, 6, 213, 2, 86, 134, 183, 59, 201, 41, 36, 184, 81, 171, 116, 17, 208, 185, 119, 170, 150, 169, 57, 1, 82, 116, 221, 218, 9, 242, 238, 39, 82, 66, 175, 53, 114, 130, 32, 65, 152, 111, 103, 5, 1, 232, 93, 15, 97, 10, 173, 129, 197, 78, 190, 51, 227, 33, 164, 135, 85, 234, 253, 184, 70, 175, 73, 14, 235, 2, 57, 186, 116, 27, 204, 200, 18, 105, 82, 62, 160, 25, 118, 99, 21, 188, 185, 240, 104, 64, 177, 133, 137, 208, 60, 145, 2, 82, 29, 21, 101, 31, 21, 124, 176, 202, 110, 246, 222, 2, 56, 128, 255, 29, 15, 235, 35, 185, 235, 77, 30, 5, 145, 185, 36, 228, 67, 209, 222, 222, 14, 0, 109, 148, 84, 5, 14, 147, 93, 240, 216, 13, 105, 165, 71, 44, 91, 64, 173, 170, 186, 12, 233, 151, 213, 141, 39, 66, 20, 253, 69, 192, 44, 238, 226, 246, 246, 118, 192, 235, 130, 174, 225, 54, 120, 209, 31, 95, 78, 225, 74, 223, 230, 42, 181, 155, 194, 217, 238, 196, 14, 208, 99, 103, 38, 122, 73, 254, 78, 138, 192, 30, 14, 216, 189, 131, 230, 114, 168, 140, 200, 171, 50, 170, 201, 208, 200, 10, 143, 237, 244, 20, 72, 119, 6, 66, 12, 128, 35, 163, 119, 240, 185, 172, 180, 162, 170, 50, 170, 75, 41, 81, 3, 12, 115, 246, 60, 238, 57, 72, 148, 161, 84, 195, 85, 25, 229, 33, 83, 26, 80, 190, 182, 167, 184, 131, 230, 114, 168, 36, 17, 219, 131, 16, 50, 67, 103, 207, 84, 216, 254, 90, 26, 0, 0, 184, 11, 197, 117, 145, 107, 175, 161, 164, 159, 73, 92, 245, 178, 228, 90, 162, 128, 62, 22, 240, 48, 0, 142, 92, 212, 89, 183, 168, 169, 20, 222, 251, 122, 163, 124, 165, 2, 144, 174, 164, 196, 47, 92, 68, 161, 183, 182, 82, 18, 80, 191, 42, 179, 114, 13, 48, 221, 45, 96, 247, 54, 87, 181, 183, 183, 183, 195, 185, 91, 26, 64, 123, 123, 123, 59, 156, 187, 205, 85, 237, 237, 237, 237, 112, 238, 54, 87, 181, 183, 183, 183, 195, 185, 219, 92, 213, 222, 222, 222, 14, 231, 6, 160, 137, 18, 182, 97, 132, 205, 156, 23, 255, 255, 255, 255, 182, 186, 177, 187, 81, 189, 159, 125]
```
Passing the above array of integers into Cyberchef (and XORing by 0xff) yields the following PNG file:
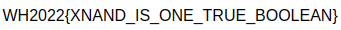
Therefore, the flag is ``WH2022{XNAND_IS_ONE_TRUE_BOOLEAN}``.
# CSIT / [Crypto] Foil the Plot
## Challenge Description
```
[Crypto] Foil the Plot
989
CSIT
6 SOLVES
DESCRIPTION
Author: Chun
Difficulty: Hard
APOCALYPSE activated a sleeper cell for a suicide bombing but the target location is not known.....
Experts from CSIT have discovered the attacker-controlled server that was used to send a secret message to the sleeper cell. The server is protected with a password that is at least 40 chars long! The server does not store the password but to our good fortune, a weakness has been discovered in the way it performs the authentication.
It validates the password by performing the following steps:
1. Split the 40 char password into 2 equally-sized segments
2. Check that the segments are not identical
3. Generate the SHA-256 digests of both segments
4. Check that the last 5 bytes of both digests are identical
Your task is to gain authentication to the server, decipher the message and determine the target location before it's too late!
Challenge Access:
http://challenges1.whitehacks.xyz:28800
http://challenges2.whitehacks.xyz:28800
Enter the flag as WH2022{ID_postal code}
Eg. WH2022{s@m_pl3_123456}
```
Note: For Step 1, if the password is more than 40 chars long, it must be divisible by 2.
## Challenge Summary
In essence, we are supposed to find a SHA256 partial hash collision between 2 strings of equal length (where each string is at least 20 chars long).
In this case, the partial hash collision refers to the last 5 bytes (or equivalently, the last 10 hexadecimal digits) of the both strings' SHA256 hash digests being equal.
More formally, we need to find 2 strings (``s1`` and ``s2``) that fulfill the following conditions:
```py
len(s1) == len(s2)
len(s1) >= 20
len(s2) >= 20
h1[-10:] == h2[-10:]
# Where h1 = SHA256 Hex Digest of s1, h2 = SHA256 Hex Digest of s2
```
## Collision Algorithm?
Since we are working with SHA256 hashes for this challenge (which is generally regarded to be quite strong), and not a weaker hashing algorithm (e.g. MD5 - which is known to exhibit [Collision Vulnerabilities](https://en.wikipedia.org/wiki/MD5#Collision_vulnerabilities)), we can make the assumption that there is no special collision attack that we should use for this challenge.
This only leaves us with one method to generate collisions - brute force.
## Naive Brute Force Algorithm
Idea: Choose a random string, ``s1``, and calculate its SHA256 hash, ``h1``. Afterwards, randomly generate a string ``s2``, and calculate its SHA256 hash, ``h2``. If the 5 byte suffixes of ``h1`` and ``h2`` are not equal, re-generate another string ``s2`` and repeat the process.
This brute force algorithm is quite commonly used as a form of proof-of-work (PoW) verification to prevent people from DDoSing services (see [this example](https://ctftime.org/writeup/12961)).
Due to the [Avalanche Effect](https://en.wikipedia.org/wiki/Avalanche_effect) of SHA256, it is not possible to determine exactly how many iterations this naive brute force algorithm would take. However, doing some simple math, the expected number of iterations this would take is ``256^(suffix byte length) = 256^5 = 16^10 = 2^40 = 1.10*10^12``.
If we let ``n = 2^40``, this algorithm can be said to have an (average) time complexity of ``O(n)``, and space complexity of ``O(1)``.
Under most circumstances, an algorithm with a time complexity of ``O(n)`` might be considered feasible. Unfortunately, it is not feasible in this case, as ``n`` is of magnitude ``10^12``.
According to [this benchmark](https://cryptopp.com/benchmarks.html), a 1.83 GHz CPU was able to hash approximately ``116 MB/s`` for SHA256 using the Crypto++ library. If we assume each string we are hashing is 20 bytes long, this would mean that in theory, we are able to hash about ``5,800,000`` strings per second. This means we would need around ``172,413 seconds`` (or ``47.9 hours``) to hash ``10^12`` strings.
This time could potentially be improved by using a stronger CPU, multiple instances, GPUs, or ASIC miners to be able to compute SHA256 hashes faster. However, there is a much more efficient (and less costly) approach...
## Birthday Attack
Observation: We do not need to find a _specific_ suffix (unlike PoW challenges), giving us greater freedom in choosing strings.
Idea: We can increase the probability of finding a partial hash collision by maintaining a dictionary (or hashmap) that stores hash suffix -> plaintext mappings.
This technique is known as the [Birthday Attack](https://en.wikipedia.org/wiki/Birthday_attack#Mathematics), which improves the probability of finding a collision by a square root. In other words, the (average) time complexity is reduced from ``O(n)`` to ``O(sqrt(n))``, with space complexity increasing from ``O(1)`` to ``O(sqrt(n))``.
With ``n = 2^40``, this means that the algorithm is expected to find a partial hash collision in just ``sqrt(n) = 2^20 = 1048576`` iterations, which is definitely feasible.
**Script**
```py
import random
import string
import hashlib
def genRandStr(): #Returns a random string consisting of uppercase and lowercase alphabets of length 20
return ''.join(random.choice(string.ascii_letters) for _ in range(20))
def brute():
i = 0
mp = dict() #Partial Hash -> String
while True:
s = genRandStr()
h = hashlib.sha256(s.encode('utf-8')).hexdigest()[-10:]
if i % 100000 == 0:
print(i)
i += 1
if h in mp: #Partial collision found
return s, mp[h]
mp[h] = s #Insert new entry
s1, s2 = brute()
print(s1, s2)
```
**Sample Output**
```
0
100000
200000
300000
400000
500000
600000
700000
800000
900000
1000000
1100000
1200000
1300000
XILlBSFFzFoDwkYpQuTH FPMGDhwFoNIJaWxjtQge
```
It can be shown that those 2 strings are partial hash collisions (as their 5 byte suffixes are equal):
```
SHA256(XILlBSFFzFoDwkYpQuTH) = 0x6e41548b45d9fc0365346fa437adef06dd1f65ac38fe217849570dd5e2f9ac96
SHA256(FPMGDhwFoNIJaWxjtQge) = 0xf67e3165e4ecdbfeb8c3e27a8197bcc78b37414fed585e1c7fa453d5e2f9ac96
^^^^^^^^^^
0123456789
```
## Website Submission
After concatenating the 2 strings generated above and submitting them to the website, the website returns the following base-64 encoded string:
```
7tXxvYpSWLNaRC3y3S/LMjA6y7eJUd7/L4Nmxs1omtLVW1HNMDWFU0q0Bnpv2eNujtVNA5jE+SwWZ8oNyr6Qb6rkwO6WBOyNknFBSn3TymwXuAHNvYIVSur0BJ6g4B7fD3Ip60/H32wTfRXdCmWBxg==
```
Upon further inspection, there are also additional clues in the webpage's source code:
```
<!-- key = SHA-256(1st segment) -->
<!-- iv = you should know which 16 bytes to use -->
<a class="p-3 text-decoration-none text-dark bold">UExBSU5URVhUIDw9PT4gKEFFUy1DQkMsIFNIQS0yNTYoMXN0IHNlZ21lbnQpLCBTSEEtMjU2KDJuZCBzZWdtZW50KSkgPD09PiBDSVBIRVJURVhU</a>
```
The 2nd base-64 encoded string (``UExBSU5URVhUIDw9PT4gKEFFUy1DQkMsIFNIQS0yNTYoMXN0IHNlZ21lbnQpLCBTSEEtMjU2KDJuZCBzZWdtZW50KSkgPD09PiBDSVBIRVJURVhU``) can be decoded to:
```
PLAINTEXT <==> (AES-CBC, SHA-256(1st segment), SHA-256(2nd segment)) <==> CIPHERTEXT
```
## AES
From the information above, there are a few clues on how we should obtain the flag.
1. The 2nd base-64 encoded string suggests that the plaintext (which presumably contains the flag) is encrypted using AES (CBC mode).
2. The 1st base-64 encoded string is likely the ciphertext, as it can be decoded to 112 bytes (exactly ``7*16``, which lines up nicely to 7 AES chunks)
3. The key is SHA256(s1), which is valid, as the AES key can be 128, 192, or 256 bits long.
4. The IV is SHA256(s2), which is invalid, as the IV is always 128 bits long. Referring back to the HTML comment, the IV is likely the first 128 bits of SHA256(s2) or the last 128 bits. After some testing, it can be shown that it is the first 128 bits.
**Script**
```py
import hashlib
import binascii
from Crypto.Cipher import AES
s1 = "XILlBSFFzFoDwkYpQuTH"
s2 = "FPMGDhwFoNIJaWxjtQge"
raw = "7tXxvYpSWLNaRC3y3S/LMjA6y7eJUd7/L4Nmxs1omtLVW1HNMDWFU0q0Bnpv2eNujtVNA5jE+SwWZ8oNyr6Qb6rkwO6WBOyNknFBSn3TymwXuAHNvYIVSur0BJ6g4B7fD3Ip60/H32wTfRXdCmWBxg=="
ct = binascii.a2b_base64(raw)
h1 = hashlib.sha256(s1.encode('utf-8')).hexdigest()
h2 = hashlib.sha256(s2.encode('utf-8')).hexdigest()
h2 = h2[:32]
cipher = AES.new(binascii.unhexlify(h1), AES.MODE_CBC, iv = binascii.unhexlify(h2))
print(cipher.decrypt(ct))
```
**Output**
```
b'[ID: h@$h_c011i$i0n] It is a tiger. It is also a leopard. It is the route to a chilling glimpse of hell.\x08\x08\x08\x08\x08\x08\x08\x08'
```
Therefore, the first part of the flag (the "ID" referred to in the challenge description) is ``h@$h_c011i$i0n``.
The second part of the flag is supposed to be a postal code, which after some guessing turned out to be the location described in the rest of the plaintext ("It is a tiger. It is also a leopard. It is the route to a chilling glimpse of hell."), which is Haw Par Villa (postal code 118628).
As such, the complete flag is ``WH2022{h@$h_c011i$i0n_118628}``.
## Complete Script
```py
import random
import string
import hashlib
import binascii
from Crypto.Cipher import AES
import requests
def genRandStr(): #Returns a random string consisting of uppercase and lowercase alphabets of length 20
return ''.join(random.choice(string.ascii_letters) for _ in range(20))
def brute():
i = 0
mp = dict() #Partial Hash -> String
while True:
s = genRandStr()
h = hashlib.sha256(s.encode('utf-8')).hexdigest()[-10:]
if i % 100000 == 0:
print(i)
i += 1
if h in mp: #Partial collision found
return s, mp[h]
mp[h] = s #Insert new entry
s1, s2 = brute()
print(s1, s2)
html = requests.get('http://challenges1.whitehacks.xyz:28800/verify?password=' + s1 + s2).text
print(html)
raw = html[2258:-701] #Extract the base-64 encoded AES ciphertext
print(raw)
ct = binascii.a2b_base64(raw)
h1 = hashlib.sha256(s1.encode('utf-8')).hexdigest()
h2 = hashlib.sha256(s2.encode('utf-8')).hexdigest()
h2 = h2[:32]
cipher = AES.new(binascii.unhexlify(h1), AES.MODE_CBC, iv = binascii.unhexlify(h2))
print(cipher.decrypt(ct))
```
## Afterthoughts
To a certain extent, this challenge is quite similar to Meet where? Middle Road?, in the sense that this challenge's Birthday Attack is similar to Meet where? Middle Road?'s MITM Attack.
Both challenges involve reducing the time complexity of a (naive) Brute Force Attack by a square root through the use of hashmaps.
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet