---
title: 【時間序列分析】Ch2：隨機過程與定態
image: https://ppt.cc/flVaux@.jpg
---

# 【時間序列分析】Ch2：隨機過程與定態

在時間序列的資料蒐集中，我們可以採集到一組資料 $\{y_1, y_2,\dots, y_t \}$，這組「觀察值」是我們看到某一種資料形成過程 (DGP) 所顯現出的結果，而這個 DGP 會和時間有所關聯，這就是簡單的隨機過程概念。

我們可以將時間看作是從過去到為來都是「無窮的」，我們只是在浩蕩的時間長河中擷取一段樣本，以此去窺探整條時間線。

:::info 
以隨機樣本來表示，就是 $\{Y_1, Y_2,\dots, Y_n \}$ 是 $\{ \dots, Y_{t-1}, Y_t, Y_{t+1}, \dots \}$ 的**子集**。而我們可以用某種聯合機率分配來描述 $\{Y_t, Y_{t+1},\dots, Y_{t+l} \},\ \forall t \in \mathbb{Z}^+$。
:::

# 2.1 隨機過程

## 2.1.1 機率空間
在做隨機試驗時，譬如擲一顆骰子，我們並不知道試驗之後會擲出什麼數字，而這個「隨機性」，就被我們使用**隨機變數**的這個概念去做描述，但從機率論的觀點，我們可以更仔細地去說明擲骰子這件事情所代表的意義，那這就得從機率空間開始說起。

一個機率空間可以表示為 $(\Omega,\mathcal{F},\mathbb{P})$，以下將分別進行解釋：

**1. 樣本空間 sample space $\Omega$**

樣本空間為該隨機試驗「**所有**」的「**可能出象 (possible outcomes)**」的集合 (set)，以 $\Omega$ 表示，而裡面的某個樣本點必然符合 $\omega \in \Omega$。

:::info
樣本空間之外的事件 (events) 都是空集合 $\emptyset$。
:::

**2. σ 代數 σ−algebra (or σ−field) $\mathcal{F}$**

σ−algebra $\mathcal{F}$ 是樣本空間 $\Omega$ 的「子集 (subset)」所構成的集合，如果這個集合滿足以下三點：

i. $\emptyset \in \mathcal{F}$
ii. 如果事件 $A_1,A_2,\dots\in \mathcal{F}$ ，則 $\bigcup_{i=1}^\infty A_i \in \mathcal{F}$
iii. 如果 $A \in \mathcal{F}$，則 $A^c \in \mathcal{F}$

:::info
結合 $\Omega$ 與 $\mathcal{F}$ 的定義對空集合 $\emptyset$ 的描述，可得 $\Omega^c = \emptyset , \Omega \in \mathcal{F}$。
:::

**3. 機率測度 probability measure $\mathbb{P}$**

一個在 $(\Omega,\mathcal{F})$ 的機率測度 $\mathbb{P}$，為 $\mathbb{P}:\mathcal{F} \rightarrow [0,1]$ 滿足：

i. $P(\Omega) = 1$
ii. 此機率測度 $\mathbb{P}$ 「可數無限可加」。
也就是說，若 $\{ A_j \}_{j \in \mathbb{N}}$，為 $\mathcal{F}$ 中的一個互斥序列 (i.e. $A_i \cup A_j = \emptyset, \forall i \neq j$ )，則
$$P(\bigcup_{i=1}^{\infty} A_i) = \sum_{i=1}^{\infty}P(A_i)$$

:::info
$P(\Omega) = 1$ 隱含 $0 \leq P(A) \leq 1$，因為 $\Omega$ 為所有可能出象的聯集。
:::

若對以測度論為基礎所建構的機率論有興趣，可以進一步閱讀[**顏國勇（2011）**](https://library.math.ncku.edu.tw/documents/1/Probability21A.pdf)。

## 2.1.2 隨機變數與隨機向量

**1. 隨機變數 random variable**
令 $(\Omega, \mathcal{F}, \mathbb{P})$ 為一(完備的)機率空間，函數 $X:\Omega \rightarrow \mathbb{R}$，而對於元素 $\omega \in \Omega$，隨機變數 $X$ 為 $\Omega$ 上的一隨機變數，其有唯一對應的實數 $X(\omega) = x$，隨機變數的值域就可以想成是隨機樣本的「樣本空間」。

而我們可以接續定義隨機變數的**分配函數 (distribution finction)**：

$$F(X \leq x) = P(\omega:X(\omega) \leq x)$$

關於隨機變數的基本觀念，在初等統計學課程應有所介紹，這邊就不多做贅述。若想做些基本複習可見筆者的初等統計學[講義](https://oceanic-phosphorus-8b7.notion.site/111-1-7a1c9cae73d84d41a71a5c973d126309)。

**2. 隨機向量 random vector**

若 $X_1,X_2,\dots , X_n$ 都是在 $\mathcal{F}$ 上的隨機變數，則我們說 $\mathbf{X} = (X_1,X_2,\dots , X_n)$ 為**隨機向量(random vector)**。在數學就是一個多維函數的映射：

$$\mathbf{X}: \Omega \rightarrow \mathbb{R}^k$$

## 2.1.3 隨機過程

有著前面的先備知識，我們可以較為容易地去認識何為隨機過程。隨機過程是在機率空間 $(\Omega, \mathcal{F}, \mathbb{P})$ 中，**一系列隨著時間變化**的隨機變數 $\{ X_t, t \in T \}$。通常我們會將參數集中的參數 $t \in T$ 想成是「時間」，可以是非負整數、非負實數、整數、實數線。

我們可以把隨機過程 $\{ X_t, t \in T \}$ 當成是二元函數 $\Omega \times T \rightarrow \mathbb{R}$，寫作 $\{ X(t,\omega,t \in T, \omega \in \Omega)  \}$。Kolmogorov 證明了一系列隨機樣本點可以找到他們所對應的隨機過程，證明見此[連結](https://www.math.lsu.edu/~sengupta/7360f09/kolmogorov.pdf)。

因此，隨機過程是一系列隨時間變化的 DGP，而我們所觀測到的時間序列資料，就可以想成是隨機過程的一個實現值。關於隨機過程的部分，至此打住暫且不往下談，若對隨機過程有興趣，可以參閱交大陳伯寧老師的[線上課程](https://www.youtube.com/playlist?list=PLj6E8qlqmkFvw7Rt63yBqai2HmPKF0V0J)。

# 2.2 定態時間序列

正如我們的目標，我們希望時間序列資料是可以被預測的，如果資料生成過程並不穩定，一直換來換去，那我們將難以用過去的資料去預測未來。在此，我們稱這種穩定的時間序列結構稱之為「**定態 (stationary)**」。

## 2.2.1 嚴格定態 
若時間序列 $\{ Y_t \}$ 為**嚴格定態 (strict stationary)**，則表示此時間序列的「**聯合**機率分配」**不會因為時間點「移動」而變化**。

也就是說，若我們現在有一個時間序列 $\{ Y_t \}$，給定時間點 $(t_1,t_2,\dots,t_n)$，對於任何 $k$ 的移動 (shift)，有以下性質：

$$(Y_{t_1},Y_{t_2},\dots,Y_{t_n})' \stackrel{d}{=}
(Y_{t_{1}+k},Y_{t_{2}+k},\dots,Y_{t_{n}+k})'$$

或者可以寫成
$$F_{Y_{t_1},Y_{t_2},\dots,Y_{t_n}}(\cdot) = F_{Y_{t_{1}+k},Y_{t_{2}+k},\dots,Y_{t_{n}+k}}(\cdot)$$

則稱時間序列 $\{ Y_t \}$ 是一個**嚴格定態 (strict stationary)** 的時間序列。

:::success
💡 若時間序列 $\{ Y_t \}$ 為 **i.i.d. (independent and identically distributed)**，則時間序列 $\{ Y_t \}$ 為嚴格定態的時間序列。

:::spoiler 推導

$$\begin{align*}
  F_{Y_{t_1},Y_{t_2},\dots,Y_{t_n}}(\cdot) 
  &= F_{Y_{t_1}}(y_{t_1})F_{Y_{t_2}}(y_{t_2})\times             \cdots \times F_{Y_{t_n}}(y_{t_n})\\
  &=F_{Y_{t_{1}+k}}(y_{t_{1}+k}) F_{Y_{t_{2}+k}}(y_{t_{2}+k}) \times  \cdots \times F_{Y_{t_{n}+k}}(y_{t_{n}+k}) \\
  &= F_{Y_{t_{1}+k},Y_{t_{2}+k},\dots,Y_{t_{n}+k}}(\cdot)
 \end{align*}$$

透過獨立性拆解聯合機率分配函數，再用同質性進行時間點的移動，最後再用獨立性合成新的聯合機率分配函數。
:::

嚴格定態 -> 相同分配

:::success
💡 若時間序列 $\{ Y_t \}$ 為嚴格定態，則 $\{ Y_t \}$ 具有相同分配，但未必為獨立之隨機變數。

:::spoiler 想法
根據嚴格定態的定義，我們可以寫出：

$$Y_t \stackrel{d}{=} Y_{t+1}$$
此式對於任何時點 $t$ 皆成立。

也就是說

$$\begin{align*}
 & Y_1 \stackrel{d}{=} Y_{1+1} =Y_2 \\ 
 & Y_2 \stackrel{d}{=} Y_{2+1} = Y_3 \\
  & \cdots \\
  & Y_n \stackrel{d}{=} Y_{n+1} \\
  & \cdots 
 \end{align*}
$$

因此可以得到 $\{ Y_t \}$ 具有相同分配。

但這不保證 $\{ Y_t \}$ 具備獨立性，因為嚴格定態表示

\begin{align*}
  F_{Y_1,Y_2}(\cdot) \stackrel{d}{=} F_{Y_3,Y_4}(\cdot)
 \end{align*}
並沒有代表
\begin{align*}
  F_{Y_1,Y_2}(\cdot) \stackrel{?}{=} F_{Y_1}(\cdot) F_{Y_2}(\cdot)
 \end{align*}

除非我們知道時間序列的聯合機率分配是服從一個如多元常態分配一樣可以分拆成個別元素的機率密度函數相乘。
:::

:::success
💡 嚴格定態時間序列之函數變換仍然為嚴格定態。
亦即：
若時間序列 $\{ Y_t \}$ 為嚴格定態，則
$$X_t = g(Y_t,Y_{t-1},Y_{t-2},\dots)$$

也是嚴格定態。
證明可見 Hansen (2021) 章節 [14.47](https://web.econ.keio.ac.jp/staff/hk/ecm2/resume/Hansen21Econometrics.pdf)。
:::

## 2.2.3 弱定態

嚴格定態在實務上驗證較不容易，我們在此介紹較好在資料上驗證的**弱定態時間序列 (weak stationary)**，或稱共變異數定態 (covariance stationary)。

若一時間序列 $\{ Y_t \}$ 符合：
i. $E(Y_t) = \mu$，該時間序列的均數為不隨時間變動的常數。
ii. $Var(Y_t) < \infty$，該時間序列的變異數為有限。
iii. $Cov(Y_t,Y_{t-k})=E(Y_t - \mu)(Y_{t-k}-\mu )=\gamma(k)$，該時間序列的自我共變異數與時間 $t$ 無關，只和 $k$ 有關 (也就是說，$\gamma(t,k)=\gamma(k)$)。

則稱時間序列 $\{ Y_t \}$ 為**弱定態時間序列**。

除了以上條件之外，弱定態時間序列$\{ Y_t \}$ 還有以下性質：

1. 變異數為常數，與不隨時間改變

$$Var(Y_t) = Cov(Y_t,Y_{t-0} = \gamma(0) = Cov(Y_{t-k},Y_{t-k-0})=Var(Y_{t-k})$$

2. $k$ 階自我相關函數是 $k$ 的函數

$$\rho(k) = \frac{Cov(Y_t,Y_{t-k})}{\sqrt{Var(Y_t)\cdot Var(Y_{t-k})}}=\frac{Cov(Y_t,Y_{t-k})}{\sqrt{Var(Y_t)\cdot Var(Y_{t})}}=\frac{\gamma(k)}{\gamma(0)}$$

3. 自我共變異函數與自我相關函數具有對稱性

$$\gamma(-k) = Cov(Y_{t+k},Y_t) = Cov(Y_t,Y_{t-k})=\gamma(k)$$

同理

$$\rho(-k)  = \rho(k)$$

:::info
對於定態的強度而言，i.i.d 大於嚴格定態又大於弱定態。但時間序列為嚴格定態並不一定隱含其為若定態，必須加上 $E(Y_t^2)<\infty$ 的條件才可以滿足。

:::

對於定態時間序列的檢定，通常會使用 ADF 檢定單根問題，未來將會補充說明。

# 2.3 白噪音

## 2.3.1 白噪音的定義
[**白噪音 (white noise)**](https://zh.wikipedia.org/wiki/File:White_noise.ogg) 是一個相當重要且基礎的時間序列形式，通常會定義如下：

給定時間序列資料 $\{\varepsilon_t\}$ 符合：  

1. $E(\varepsilon_t)=0$，均數期望值為 0。
2. $E(\varepsilon_t^2) = Var(\varepsilon_t) = \sigma^2$，變異數 (二階動差) 為常數。
3. $E(\varepsilon_t \varepsilon_{t-k})=0$

以上三點對任何 $t,k$ 皆成立，則稱 $\{\varepsilon_t\}$ 為白噪音，以 $\varepsilon_t \sim WN(0,\sigma^2)$ 表示。

:::success
💡 白噪音符合弱定態時間序列的條件。
:::spoiler 證明
1. $E(\varepsilon_t) =\mu = 0$
2. $Var(\varepsilon_t) = E(\varepsilon_t^2) - E(\varepsilon_t)^2 = \sigma^2-0 = \sigma^2 < \infty$
3. $Cov(\varepsilon_t,\varepsilon_{t-k}) = E(\varepsilon_t\varepsilon_{t-k})-E(\varepsilon_t)E(\varepsilon_{t-k})=0 - 0\times 0=0$

因此符合弱定態的條件。
:::

另外，我們也可以對於白噪音 $\{\varepsilon_t\}$ 給予更嚴格的定義：
若 $\varepsilon_t \overset{\mathrm{i.i.d.}}{\sim} (0,\sigma^2)$，則稱 $\{\varepsilon_t\}$ 為白噪音。

此時因 i.i.d. 的性質，表示前後期資料為獨立事件，因此我們無法透過過去的資訊集 $\Omega_t = \{\varepsilon_t,\varepsilon_{t-1},\dots  \}$ 去預測未來，亦即：
$$E(\varepsilon_{t+1}) = E(\varepsilon_{t+1}|\varepsilon_t,\varepsilon_{t-1},\dots  ) =E(\varepsilon_{t+1})=0$$

## 2.3.2 白噪音與隨機漫步
已知時間序列 $\{X_t\}$ 是白噪音，也就是 $\{X_t\}\overset{\mathrm{i.i.d.}}{\sim} (0,\sigma^2)$。
若今令 $Y_0 = 0$，且 $Y_t = X_1 + X_2 +\cdots+X_t = \sum_{i=1}^tX_i$ 。
即
$$\begin{align*}
 Y_0 &= 0 \\
 Y_1 &= X_1  \\
 Y_2 &= X_1 + X_2 \\
 Y_3 &= X_1 + X_2 + X_3 \\
 & \cdots \\
 Y_t &= \sum_{i=1}^tX_i\\
 \end{align*}$$

我們先來看 $\{Y_t\}$ 是否符合 (弱) 定態的條件：

試著先寫出各項的一階與二階動差：
$$\begin{align*}
& E(Y_1) = 0,\ Var(Y_1) = \sigma^2 \\
& E(Y_2) = 0\\ 
& Var(Y_2)= Var(X_1+X_2)=Var(X_1) + Var(X_2) + 2Cov(X_1,X_2) =\sigma^2+\sigma^2 +0 = 2 \sigma^2\end{align*}$$

以此類推

$$\begin{align*}
& E(Y_3) = 0,\ Var(Y_3) = 3\sigma^2 \\
& E(Y_4) = 0,\ Var(Y_4) = 4\sigma^2 \\
& \cdots  \\
& E(Y_t) = 0,\ Var(Y_t) = t\sigma^2
\end{align*}$$

一階動差皆為 $0$，二階動差皆為有限。

接著計算共變異數

$$\begin{align*}
Cov(Y_1,Y_2) &= Cov(X_1,X_1+X_2)= Var(X_1) + Cov(X_1,X_2) \\
             &= \sigma^2 + 0 = \sigma^2 \\
Cov(Y_2,Y_3) &= Cov(X_1+X_2,X_1+X_2+X_3) = Var(X_1) + Var(X_2) +0\\
             &= 2 \sigma^2
\end{align*}$$

以此得知共變異數會和 $t$ 有關，而非只是 $k$ 的函數。
**故白噪音的和，不是定態時間序列。**

我們將 $\{Y_t\}$ 換一種表達方式：

$$\begin{align*}
Y_t &= X_1 + X_2 +\cdots+X_{t-1}+X_t \\
    &= Y_{t-1} + X_t
\end{align*}$$ 

且 $X_t \sim WN(0,\sigma^2)$。

這就是財務理論中鼎鼎大名的「**隨機漫步模型 (random walk model)**」，隨機漫步也是一個最基本的「**非定態 (nonstationary)**」時間序列魔型。
若以股價作為隨機漫步的例子，對於明日 (t+1) 最佳的股價預期，就應該是今天 (t) 的股價，因為
$$E_t(Y_{t+1})=E_t(Y_{t}+X_{t+1})= Y_t+E_t(X_t+1)=Y_t$$

## 2.3.3 在 R 中模擬白噪音

有很多的機率分配函數都可以是白噪音，在此我們選擇一個最為簡單的時間序列，此時間序列由標準常態分配所組成。
也就是說時間序列 $\{\varepsilon_t\}\overset{\mathrm{i.i.d.}}{\sim} N(0,1)$。

在 R 中可以很容易地模擬出標準常態分配的樣本：

Input:
set.seed(1234) #建立種子以重現程式碼

y <- ts(rnorm(100, mean = 0, sd = 1)) #建立100筆 N(0,1) 的ts資料

plot(y, main="White noise of N(0,1)") #繪製 WN 的折線圖
abline(h=0) # 畫出 0 的水平線

Output:


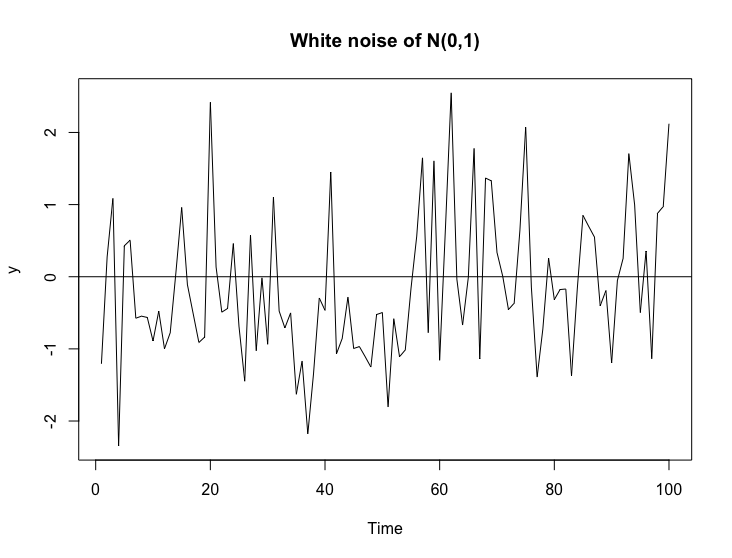
我們也可以畫出這系列白噪音的 ACF 圖：

Input:
acf(y,plot = T, main = "ACF plot of a White Noise")

Output:


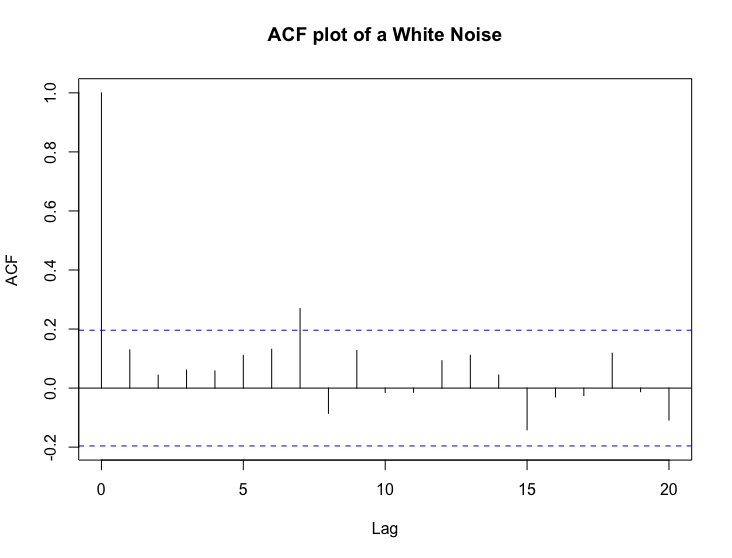
藍色虛線表示白噪音 ACF 的邊界，若資料為白噪音，我們希望 95% 的 ACF 資料不要超過此範圍 (95% 信賴區間)。
這是因為，在大樣本的情況之下，$\rho_k$ 的抽樣分配為：
$$\rho_k \overset{A}{\sim} N(0,\frac{1}{T}) $$

詳見：[Box & Pierce (1970)](https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=7cd4e19b3eeecf086574969a2cc9d5a4b987275b)。

# 參考資料
1. 陳旭昇（2022）。《時間序列分析: 總體經濟與財務金融之應用》(3版)。
3. 陳旭昇（2015）。《統計學: 應用與進階》(3版)。
4. 楊奕農（2017）。《時間序列分析: 經濟與財務上之應用》(3版)。
5. 葉小蓁（1998）。《時間序列分析與應用》。
6. [顏國勇（2011）。《機率論》，電子書。](https://library.math.ncku.edu.tw/documents/1/Probability21A.pdf)
7. [北京大學「金融時間序列分析」講義](https://www.math.pku.edu.cn/teachers/lidf/course/fts/ftsnotes/html/_ftsnotes/ftsnotes.pdf)。
8. [北京大學「金融中的随机数学」講義](https://www.math.pku.edu.cn/teachers/lidf/course/stochproc/stochprocnotes/html/_book/index.html)。
9. Klaus Neusser (2015), Time Series Analysis in Economics, Springer.
10. Jonathan D. Cryer and Kung-Sik Chan (2008), Time Series Analysis with Applications in R, Springer.
11. Paul S.P. Cowpertwait and Andrew V. Metcalfe (2009), Introductory Time Series with R, Springer.
12. Walter Enders (2015), Applied Econometric Time Series, Wiley.
13. [Christoph Hanck, Martin Arnold, Alexander Gerber, and Martin Schmelzer(2024), Introduction to Econometrics with R.](https://www.econometrics-with-r.org/index.html)
14. Bruce E. Hansen (2021), Econometrics, Princeton University Press.
15. Steven Shreve (2003), Stochastic Calculus for Finance”, Vol 2, Springer.
16. [Rao, S. S. (2008). A course in time series analysis. In Technical Report. Texas A&M University.](https://web.stat.tamu.edu/~suhasini/teaching673/time_series.pdf)