【時間序列分析】Ch5：自我迴歸模型

--- title: 【時間序列分析】Ch5：自我迴歸模型 image: https://ppt.cc/flVaux@.jpg --- # 【時間序列分析】Ch5：自我回歸模型在時間序列研究中，常會看到所謂「**ARMA**」模型，MA 即是移動平均，我們在 Ch4 中有做詳細的介紹，而 AR 是表示「自我迴歸 (autoregressive)」的意思，那是因為在傳統回歸中，我們認為殘差項是 i.i.d. 的，但是在時間序列資料中，卻是跨期間存在「自我相關」，而 AR 模型則是直接將該隨機變數的歷史資料作為解釋變數。 # 5.1 一階自我迴歸模型 AR(1) ## 5.1.1 何為 AR(1) 如同我們先前對於 MA(1) 的表示一樣，**AR(1)** 表示我們用「**前一期**」的資料值來「**預測下一期**」的資料值，而 AR(1) 是非常常見的一個預測模型。 **AR(1)** 的模型設定如下： $$Y_t = \beta_0 +\beta_1 Y_{t-1} +e_t$$ 其中，$\{e_t\}\sim WN(0,\sigma^2)$ 且為具**遍歷性**的**嚴格定態**時間序列。在迴歸模型中，對係數的解釋是很重要的，$\beta_1$ 的值可說是決定該時間序列走向的重要變因，$\beta_1$ 被稱為**一階自我迴歸係數 (first order coefficient)**。 - 若 $\beta_1\to 0$，則時間序列 $\{Y_t\}$ 會退化成白噪音。 - 隨著 $|\beta_1|$ 升高，對下一期的預測會持續帶有前幾期誤差項的資訊 (以 MA 序列的方式)，這會使得該過程會相較起來更平滑。透過反覆迭代，我們可以得出 AR(1) 模型的組成： $$\begin{align} Y_t &= \beta_0 + \beta_1 Y_{t-1} + e_t \\ &= \beta_0 + \beta_1 (\beta_0 + \beta_1 Y_{t-2} + e_{t-1}) + e_t \\ &= \beta_0 + \beta_1 (\beta_0 + \beta_1 (\beta_0 + \beta_1 Y_{t-3} + e_{t-2}) + e_{t-1}) + e_t \\ &= (1+\beta_1+\beta_1^2)\beta_0+ \beta_1^3 Y_{t-3} + \beta_1^2 e_{t-2} + \beta_1 e_{t-1} + e_t \\ & \cdots \text{繼續迭代} \\ &= \sum_{j=0}^n \beta_1^j \beta_o + \sum_{j=0}^n \beta_1^j e_{t-j} + \beta_1^{n+1}Y_{t-(n+1)} \\ & \text{as}\ n \to \infty \text{,} \\ &= \sum_{j=0}^\infty \beta_1^j \beta_o + \underbrace{\sum_{j=0}^\infty \beta_1^j e_{t-j} }_{\text{MA}(\infty) \text{ process}}+ \lim_{n \to \infty} \beta_1^{n+1}Y_{t-(n+1)} \end{align}$$ 若此時，我們要求 $|\beta_1| < 1$，則 $$\begin{align} Y_t &= \beta_0 + \beta_1 Y_{t-1} + e_t \\ &= \sum_{j=0}^\infty \beta_1^j \beta_o + \underbrace{\sum_{j=0}^\infty \beta_1^j e_{t-j} }_{\text{MA}(\infty) \text{ process}}+ \underbrace{\lim_{n \to \infty} \beta_1^{n+1}Y_{t-(n+1)} }_{\to 0} \\ &=\underbrace{ \frac{\beta_0}{1-\beta_1} }_\mu+ \sum_{j=0}^\infty \beta_1^j e_{t-j} \\ &= \mu + \sum_{j=0}^\infty \beta_1^j e_{t-j} \end{align}$$ 也就是說，**我們可以用 MA(∞) 模型去逼近 AR(1) 模型**，至於 AR 與 MA 之間的對偶關係會在後面進行解說。 :::info **AR(1) 的定態條件**為 $|\beta_1|<1$，我們可以先用 MA 模型的想法去理解，本章後半部分會介紹所謂「**單根**」。 ::: :::info 若 **AR(1)** 係數 $\beta_1 > 1$，則此 AR(1) 過程會**發散**或稱**爆炸** (explosive)，但在實證研究上鮮少出現此情形。 ::: :::success 💡 **用落後運算子來描述 AR(1)** $$\begin{align} Y_t &= \beta_0 + \beta_1 Y_{t-1} + e_t \\ &= \beta_0 + \beta_1 \color{red}{L Y_t} +e_t \\ \end{align}$$ 進行移項，(令多項式 $\beta(L) = 1-\beta_1 L$) $$\begin{align} & \color{red}{(1-\beta_1 L)}Y_t = \beta_0 + e_t \\ & \Rightarrow \\ &\color{red}{\beta(L) }Y_t = \beta_0 + e_t \end{align}$$ 也就是說，若 AR(1) 是可逆的，則下式成立 $$Y_t = \frac{1}{\beta(L)} (\beta_0 + e_t) = {\beta(L)}^{-1} (\beta_0 + e_t) $$ 此外，$\frac{1}{\beta(L)} = \frac{1}{1-\beta_1 L}$，用無窮等比級數公式去反推的話，即為首項為 $1$ 且公比為 $\beta_1 L$ 的無窮等比級數。也就是說， $$\sum_{j=0}^\infty (\beta_1 L)^j = \sum_{j=0}^\infty \beta_1^j L^j = \frac{1}{1-\beta_1 L} = {\beta(L)}^{-1}$$ 那再根據上面的想法，AR(1) 的公式可進行以下改寫： $$\begin{align} Y_t &= {\beta(L)}^{-1} (\beta_0 + e_t) \\ &= \sum_{j=0}^\infty \beta_1^j L^j (\beta_0 + e_t) \\ &= \beta_0 \sum_{j=0}^\infty \beta_1^j + \sum_{j=0}^\infty \beta_1^je_{\color{red}{t-j}} \\ &= \frac{\beta_0}{1-\beta_1} + \sum_{j=0}^\infty \beta_1^je_{\color{red}{t-j}} \end{align}$$ 如此便是連結 AR(1) 與 MA(∞) 的另外一種視角。 ::: ## 5.1.2 AR(1) 的動差性質我們進一步去研究 AR(1) 的動差性質 (給定 $|\beta_1|<1$)： - 均數：$E[Y_t] = \mu + 0 +0+0+\cdots = \mu =\frac{\beta_0}{1-\beta_1}$ - 變異數：$Var[Y_t] =\gamma(0) = \sigma^2[1+\beta_1^2+\beta_1^4 +\cdots] = \frac{\sigma^2}{1- \beta_1^2 } < \infty$ - 自我共變異數： $$\begin{align} \gamma(j) &= Cov(Y_t,Y_{t-j}) \\ &= Cov(\beta_0 + \beta_1 Y_{t-1} + e_t,Y_{t-j})\\ &= \underbrace{Cov(\beta_0,Y_{t-j})}_0 + \beta_1 Cov(Y_{t-1},Y_{t-j}) +\underbrace{ Cov(e_t,Y_{t-j})}_0 \\ &= \beta_1 Cov(Y_{t-1},Y_{t-j}) \\ &= \beta_1 \gamma(j-1) \end{align}$$ 上式透過 AR(1) 為定態的條件後成立 (弱定態的性質)。因此， $$\begin{align} \gamma(j) &= Cov(Y_t,Y_{t-j}) \\ &= \beta_1 \gamma(j-1) \\ &= \beta_1^j \gamma(j-j) = \beta_1^j \gamma(0)\\ &= \beta_1^j \times \frac{\sigma^2}{1- \beta_1^2 } \\ &= \frac{\beta_1^j \sigma^2}{1- \beta_1^2 } < \infty \end{align}$$ - 自我相關係數： $$\rho(k) = \beta_1^k = \frac{\gamma(k)}{\gamma(0)}$$ ## 5.1.3 隨機漫步與單根我們先前在 [**Ch2**](https://hackmd.io/@wwwh0225/rykeLBkLC#232-%E7%99%BD%E5%99%AA%E9%9F%B3%E8%88%87%E9%9A%A8%E6%A9%9F%E6%BC%AB%E6%AD%A5) 及 [**Ch3**](https://hackmd.io/@wwwh0225/S1dYUeA4R#343-%E9%9E%85%E8%88%87%E9%9A%A8%E6%A9%9F%E6%BC%AB%E6%AD%A5) 在介紹白噪音和鞅時有先初步提到了隨機漫步模型，以下為一個簡單隨機漫步模型： $$Y_t = Y_{t-1} + e_t,\ e_t \overset{\mathrm{i.i.d.}}{\sim} (0,\sigma^2)$$ 亦即**時間序列當期之值為前一期之值再加上一個隨機誤差項**，從上面這個表達式應該可以看出其與 **AR(1)** 模型有著異曲同工之架構。 **AR(1)**：$Y_t = \beta_0 + \beta_1 Y_{t-1} + e_t$ 當 $\beta_0 =0$ 及 $\beta_1 =1$ 時，**AR(1)** 模型即退化 (reduce) 為簡單**隨機漫步**模型。若$\{Y_t\}$ 是一個簡單隨機漫步的時間序列，且序列之**初始值 (initial value)** 為 $Y_0$，則經過反覆迭代： $$Y_t = Y_{t-1} + e_t = Y_{t-2} +e_{t-1} +e_t = \cdots =Y_0 + \sum_{j=1}^{t}e_j$$ 也就是說，$Y_t$ 的值是由 $Y_0$ 與一系列的隨機衝擊所構成。綜上，一個**簡單隨機漫步過程**有以下**性質**： - 隨著時間 $t$ 增加，隨機衝擊 $e_0$ 對 $Y_t$ 的影響不會消失。 - 此過程**不為定態**，因為 $Var[Y_t] = Var[Y_0] + t \sigma^2$。 - 此過程**不可逆**，即 $\beta(z)=1-z$ 不可逆，也就是說隨機漫步無法使用 MA 的形式作表示。 - 此過程不會「均值回歸 (Mean Reversion)」，隨著時間變長，價格並不會回到均數，因為所受到之隨機衝擊持續存在。 --- 接著，讓我們介紹「**具有飄移項**」之**隨機漫步**模型 **(random walk model with drift)**： $$Y_t = \underbrace{\beta_0}_{\text{drift}}+ Y_{t-1} + e_t,\ e_t \overset{\mathrm{i.i.d.}}{\sim} (0,\sigma^2)$$ 其中，飄移項 $\beta_0 \neq 0$。 <img style="display: block; margin: auto;" src="https://financetrain.sgp1.cdn.digitaloceanspaces.com/random-walk-3.png" width="100%"> <p style="text-align: center;"> <a href="https://financetrain.com/simulate-random-walk-rw-in-r ">Random walk model with drift</a> </p> 讓我們再拿出 AR(1) 進行對比：$Y_t = \beta_0 + \beta_1 Y_{t-1} + e_t$ 同樣地，當 $\beta_1 =1$ 時，**AR(1)** 模型即退化為**具有飄移項之隨機漫步**模型。若我們透過落後運算子多項式 (lag polynomial) 來表示 AR(1)： $$Y_t = {(1-\beta_1L)}^{-1} (\beta_0 + e_t) = {\beta(L)}^{-1} (\beta_0 + e_t) $$ 其中，lag polynomial ${\beta(L)} = 1-\beta_1L$，讓我們轉為一般性的多項式表示： $$\beta(z) = 1-\beta_1 z$$ 我們說 AR(1) 具有單根，即為解方程式 $\beta(z)=0$，有出現根 $\color{red}{z=1}$。 ($z=1$ 則表示 $\beta_1 = 1$，也就是 AR(1) 是具有飄移項之隨機漫步模型，即具有隨機趨勢) 所謂時間序列的「**單根**」即表示該序列具有「**隨機趨勢**」，因此是一個**非定態**的時間序列。 :::info 上列方程式 $\beta(z)=0$ 可被稱為 AR(1) 的「**特徵方程 (characteristic equation)**」。詳見：[Magee (2008)](https://socialsciences.mcmaster.ca/magee/761_762/other%20material/unit%20and%20char%20roots.pdf)。 ::: # 5.2 p 階自我迴歸模型 AR\(p) AR(1) 是透過「前一期」的數值作為資訊來做為當期的預測，若我們想要囊括更多期的資訊進來，是為 **AR\(p)** 模型。 ## 5.2.1 AR(2) 模型讓我們先以 **AR(2)** 模型作為一個開端： $$Y_t = \beta_0 + \beta_1 Y_{t-1} + \beta_2 Y_{t-2} +e_t $$ 其中，$\{e_t\}\sim WN(0,\sigma^2)$ 且同樣為具**遍歷性**的**嚴格定態**時間序列。若 **AR(2)** 是一個**定態**的時間序列，其重要動差如下： - 均數：因為 AR(2) 為定態，因此 $E(Y_t)=\mu,\ \forall t$。 $$\begin{align} &E(Y_t) = \beta_0 + \beta_1 E(Y_{t-1}) + \beta_2 E(Y_{t-2}) +E(e_t) \\ \Rightarrow & \mu = \beta_0 + \beta_1 \mu + \beta_2 \mu+0 \\ \Rightarrow & \mu =\frac{\beta_0}{1-(\beta_1+\beta_2)} \end{align}$$ - 變異數與自我共變異數：同樣使用 AR(2) 的定態條件（$Var[Y_t] = \gamma(0)$、$Cov(Y_t,Y_{t-k}=\gamma(k),\ \forall t$）： $$\begin{align} Var[Y_t] =\gamma(0) &= Var[ \beta_0 + \beta_1 Y_{t-1} + \beta_2 Y_{t-2} +e_t ] \\ &= \beta_1^2 Var[Y_{t-1}] + \beta_2^2 Var[Y_t] + Var[e_t] \\ &+2 \beta_1 \beta_2 Cov(Y_{t-1},Y_{t-2}) +2\beta_1 Cov(Y_{t-1},e_t)+2\beta_2 Cov(Y_{t-2},e_t) \\ &= \beta_1^2 \gamma(0) + \beta_2^2 \gamma(0) +\sigma^2 + 2\beta_1 \beta_2 \gamma(1)+0 +0 \\ &= (\beta_1^2 + \beta_2^2)\gamma(0)+ \sigma^2 +2 \beta_1 \beta_2 \gamma(1) \end{align}$$ $$\begin{align} Cov[Y_t,Y_{t-1}] =\gamma(1) &= Cov(\beta_0 + \beta_1 Y_{t-1} + \beta_2 Y_{t-2} +e_t,Y_{t-1}) \\ &=\beta_1Var(Y_{t-1})+\beta_2Cov(Y_{t-2},Y_{t-1})+Cov(e_t,Y_{t-1}) \\ &= \beta_1 \gamma(0) + \beta_2 \gamma(1) + 0 \\ &= \beta_1 \gamma(0) + \beta_2 \gamma(1) \end{align}$$ 因此我們可解下列二元一次聯立方程式： $$ \left\{ \begin{array}{lr} \gamma(0) = (\beta_1^2+\beta_2^2)\gamma(0)+\sigma^2 +2 \beta_1 \beta_2 \gamma(1) \\ \gamma(1) = \beta_1 \gamma(0) + \beta_2 \gamma(1) \end{array} \right. $$ 得： $$ \left\{ \begin{array}{lr} \gamma(0) = (\frac{1-\beta_2}{1+\beta_2})(\frac{\sigma^2}{(1-\beta_2)^2-\beta_1^2}) \\ \gamma(1) = \frac{\beta_1}{1-\beta_2}\gamma(0) \end{array} \right. $$ ## 5.2.2 AR(2) 的定態條件 AR(2) 的定態條件其實與 AR(1) 雷同，其重點是在於在時間 $t$ 越來越長時，不可以使模型發散，同樣可以用 AR polynomial 的方式去描述 [**AR(2)**](https://www.fsb.miamioh.edu/lij14/672_ar2.pdf) 模型： $$\begin{align} Y_t &= \beta_0 + \beta_1 Y_{t-1} + \beta_2 Y_{t-2} +e_t \\ &= \beta_0 + \beta_1L Y_{t} + \beta_2 L^2 Y_{t} +e_t\\ &= \beta_0 + (\beta_1 L+\beta_2 L^2) Y_{t} +e_t \\ \Rightarrow \\ &\color{red}{(1-\beta_1L- \beta_2L^2)} Y_t= \beta_0 +e_t \\ & \color{red}{\beta(L)} Y_t= \beta_0 +e_t \end{align}$$ 因此，我們可得 AR(2) 之特徵方程式： $$\beta(z) = 1-\beta_1z- \beta_2z^2 =0$$ 這是一個一元二次方程式，我們可以針對其根透過公式解求出重根、二相異實根以及二共軛虛根之情形，我們將其因式分解成以下形式： $$\beta(z) = 1-\beta_1z- \beta_2z^2 = (1-\lambda_1z)(1-\lambda_2 z)$$ 公式解： $$z_{1,2} = \frac{\beta_1 \pm \sqrt{\beta_1^2+4\beta_2} }{-2\beta_2}$$ 其中，(分別對應) $$\lambda_{1,2} = \frac{1}{z_{1,2}} = \frac{\beta_1 \pm \sqrt{\beta_1^2 + 4 \beta_2}}{2}$$ 因此，若 $\beta(z)$ 要可逆，則 $(1-\lambda_1z)$ 和 $(1-\lambda_2z)$ 都要可逆： $$\beta(z)^{-1}=(1-\lambda_1z)^{-1}(1-\lambda_2 z)^{-1}$$ 故 $\beta(L)$ 要可逆的充分條件為：$|\lambda_1|<1$ 及 $|\lambda_2|<1$。以下我們假設 $\beta_{L}$ 可逆： $$\begin{align} & \color{red}{\beta(L)} Y_t= \beta_0 +e_t \\ \Rightarrow &Y_t = \beta(L)^{-1}(\beta_0 +e_t ) \\ &Y_t = \underbrace{ \beta(L)^{-1}\beta_0 }_{\text{covergent constant}} + \beta(L)^{-1}e_t \end{align}$$ 其中， $$\begin{align} \beta(L)^{-1}e_t &= (1-\lambda_1L)^{-1} \underbrace{(1-\lambda_2 L)^{-1} e_t}_{\text{covergent MA process}, \color{red}{u_t}} \\ &= \underbrace{(1-\lambda_1L)^{-1} \color{red}{u_t}}_{\text{covergent MA process as well}} \end{align}$$ 如此，當 $|\lambda_1|<1$ 及 $|\lambda_2|<1$ 時，**AR(2)** 即**可逆**，其也為一個**嚴格定態**且**具遍歷性**的時間序列模型。 :::success 💡 **AR(2) 的定態區域** 透過「根與係數」的關係，我們已知 $\beta_1 = \lambda_1+\lambda_2$、$\beta_2 = - \lambda_1\lambda_2$，透過代數運算，我們可知**若且唯若 (if and only if)** 當下列情形**皆**成立時，**AR(2)** 為一個**嚴格定態**且**具遍歷性**的時間序列。 $$ \left\{ \begin{array}{lr} \beta_1 + \beta_2 < 1 \\ \beta_1 - \beta_2 < 1 \\ \alpha > -1 \end{array} \right. $$ ![AR2](https://i.imgur.com/iq0amIg.png) 註：[繪圖程式碼](https://stats.stackexchange.com/questions/118019/a-proof-for-the-stationarity-of-an-ar2)。 :::spoiler 推導已知 $$\lambda_{1,2} = \frac{1}{z_{1,2}} = \frac{\beta_1 \pm \sqrt{\beta_1^2 + 4 \beta_2}}{2}$$ 故 $|\lambda_1|<1$ 及 $|\lambda_2|<1$，可以有如下不等式： $$\begin{align} & & | \frac{\beta_1 \pm \sqrt{\beta_1^2 + 4 \beta_2}}{2}| &< 1 \\ &\Rightarrow& -1< \frac{\beta_1 \pm \sqrt{\beta_1^2 + 4 \beta_2}}{2} &< 1 \\ &\Rightarrow& -2< \beta_1 \pm \sqrt{\beta_1^2 + 4 \beta_2} &< 2 \end{align} $$ 讓我們先考慮「**兩實根**」的情境：判別式 $\beta_1^2 + 4 \beta_2 \geq 0$ 上開不等式的最大值邊界為：$\beta_1 + \sqrt{\beta_1^2 + 4 \beta_2} < 2$。此處經移項後可推導出第一條邊界：$\color{red}{\beta_2 + \beta_1 < 1}$。同樣地，該不等式的最小值邊界為：$\beta_1 - \sqrt{\beta_1^2 + 4 \beta_2} > - 2$。此處經移項後可推導出第二條邊界：$\color{red}{\beta_2 - \beta_1 < 1}$。接著考慮「**兩共軛虛根**」的情境：判別式 $\beta_1^2 + 4 \beta_2 < 0$ 此時，我們可以將 $\lambda_{1,2}$ 改成 $a+bi$ 的表達方式： $$\lambda_{1,2} = \frac{\beta_1 \pm \sqrt{\beta_1^2 + 4 \beta_2}}{2} = \frac{\beta_1}{2} \pm \frac{ \sqrt{-(\beta_1^2 + 4 \beta_2)}}{2}i$$ 並對其取[**絕對值 (模)**](https://resource.learnmode.net/upload/flip/book/6e/6e9e189b2d3e65f5/d14a057f3cab.pdf) (squared modulus)： $$|\lambda_{1,2}| = \sqrt{(\frac{\beta_1}{2})^2 + (\frac{ \sqrt{-(\beta_1^2 + 4 \beta_2)}}{2})^2) }$$ 由於我們希望 $|\lambda_{1,2}| <1$，因此對於該絕對值再取平方可得下列結果： $$\begin{align} |\lambda_{1,2}|^2 &= (\frac{\beta_1}{2})^2 + (\frac{ \sqrt{-(\beta_1^2 + 4 \beta_2)}}{2})^2) \\ &= \frac{\beta_1^2}{4} + \frac{-(\beta_1^2 + 4 \beta_2)}{4} \\ &= -\beta_2 \color{red}{<1} \end{align}$$ 因此得出第三條邊界為：$\color{red}{\beta_2 > -1}$ ::: ## 5.2.3 AR\(p) 模型與定態條件當我們瞭解 AR(1)、AR(2) 後，接著便可以對更一般化的 **AR\(p)** 模型有更清楚的認識。 $$Y_t = \beta_0 + \beta_1 Y_{t-1} + \beta_2 Y_{t-2}+\cdots+\beta_p Y_{t-p} +e_t $$ 其中，$\{e_t\}\sim WN(0,\sigma^2)$ 且同樣為具**遍歷性**的**嚴格定態**時間序列。若我們使用落後運算子來表示 AR\(p)，可得： $$\begin{align} Y_t &= \beta_0 + \beta_1 Y_{t-1} + \beta_2 Y_{t-2}+\cdots+\beta_p Y_{t-p} +e_t \\ &= \beta_0 + \beta_1 L Y_t + \beta_2 L^2 Y_t +\cdots+ \beta_p L^p Y_t + e_t \\ \Rightarrow & Y_t - \beta_1 L Y_t - \beta_2 L^2 Y_t -\cdots- \beta_p L^p Y_t = \beta_0 + e_t \\ &(1-\beta_1 L -\beta_2 L^2 -\cdots-\beta_p L^p)Y_t = \beta_0 + e_t\\ \Rightarrow & \color{red}{\beta(L)}Y_t = \beta_0 + e_t \\ \Rightarrow &Y_t = \color{red}{\beta(L)^{-1}}( \beta_0 + e_t) \end{align}$$ 其中，$\beta(L) = 1-\beta_1 L -\beta_2 L^2 -\cdots-\beta_p L^p$ AR\(p) 的 auouregressive polynomial 可以一般化地表示成： $$\begin{align} \beta(z) &= 1-\beta_1 z -\beta_2 z^2 -\cdots-\beta_p z^p \\ &=(1-\lambda_1z)(1-\lambda_2z)-\cdots-(1-\lambda_pz) \end{align}$$ 我們同樣希望 $\beta(z)$ 是可逆的，可逆條件如同前面的範例，也就是 $\beta(z)^{-1} =(1-\lambda_1z)^{-1}(1-\lambda_2z)^{-1}-\cdots-(1-\lambda_pz)^{-1}$，其中 $|\lambda_j|<1,\ j=1,2,\dots,p$。 $$\begin{align} Y_t &= \color{red}{\beta(L)^{-1}}( \beta_0 + e_t) \\ &= \underbrace{ \beta(L)^{-1}\beta_0 }_{\text{covergent constant}} + \underbrace{ \beta(L)^{-1}e_t }_{\text{covergent MA process}} \end{align}$$ 因此，**若 $\beta(z)$ 可逆**，則 **AR\(p)** 為一個**嚴格定態**且**具有遍歷性**的時間序列。在 AR\(p) 模型中，我們無法如同 AR(2) 一樣透過係數 $\{\beta_j\}$ 之間的關係找到 AR\(p) 模型的定態區域，但我們可以驗證特定一組的 $\{\beta_j\}$ 是否會使 AR\(p) 模型為定態的時間序列。因此，我們會想要討論 $\{\beta_j\}$ 與 $\{\lambda_j\}$ 之間的關係：對於方程式 $\beta(z)=0$ 我們可以對其做因式分解，找到它的 p 個根： $\beta(z) =(1-\lambda_1z)(1-\lambda_2z)-\cdots-(1-\lambda_pz)=0$ 由 $(1-\lambda_jz)=0$ 可以得出其中第 $j$ 個根為：$z_j=\lambda_j^{-1}$ 故若該方程式之根為「**實根**」，假使我們要求 $|\lambda_j|<1$，則表示「根」$|z_j|>1$。當然，該方程式之根也可能存在「**虛根**」，此時「根」$|z_j|>1$ 的情況會變得稍稍複雜一點。若「虛根」$z_j = a+bi$，則 $|z_j|=\sqrt{a^2+b^2}$ 此為複數平面上 $z_j$ 與原點之距離，又我們要求 $|z_j|>1$，這如同在複數平面上畫出一個**單位圓**，而我們希望 $z_j$ 的點**落在單位圓之外**。我們同樣可以**把實根的結果放進複數平面**中，因為實數也就只是複數 $a+bi$ 當 $b=0$ 時的特例。總歸來說，**AR\(p)** 模型的**定態條件**為：方程式 $\beta(z) = 1-\beta_1 z -\beta_2 z^2 -\cdots-\beta_p z^p=0$ 之**根**的「**範數 (modulus)**」**皆落在單位圓之外**。($|z_j|>1$) 若任一方程式之根之範數小於 1，則 AR\(p) 會是一個爆炸之時間序列；若任一方程式之根之範數等於 1，則稱 AR\(p) 具有單根 (unit root)。 | <img src=https://girlsangle.wordpress.com/wp-content/uploads/2012/07/blog_072412_08.jpg width=60% />| | :--------: | | [*複數平面上的單位圓*](https://girlsangle.wordpress.com/2012/07/25/the-number-plane/) | ## 5.2.4 AR\(p) 的動差與 Yule-Walker 方程式對於一個**定態**的 **AR\(p)** 模型： $$Y_t = \beta_0 + \beta_1 Y_{t-1} + \beta_2 Y_{t-2}+\cdots+\beta_p Y_{t-p} +e_t,\ \{e_t\}\overset{i.i.d.}{\sim}WN(0,\sigma^2) $$ 對於等號兩側皆取期望值，若均數 $E[Y_t]=\mu$： $$\begin{align} \mu = \beta_0 + \beta_1 \mu + \beta_2 \mu+\cdots+ \beta_p \mu \end{align}$$ 因此， $$E[Y_t]=\mu = \frac{\beta_0}{1-\beta_1-\beta_2-\cdots-\beta_p}$$ 承上，我們接著改寫 AR\(p) 模型： $$Y_t -\mu = \beta_1 (Y_{t-1}-\mu) + \beta_2 (Y_{t-2}-\mu) + \cdots+\beta_p (Y_{t-p}-\mu) +e_t$$ 因此，AR\(p) 的 **k 階自我共變異數**可寫成﹔( $k\leq p$ ) $$\begin{align} \gamma(k)&=E[(Y_t-\mu)(Y_{t-k}-\mu)] \\ &= \beta_1E[(Y_{t-1} -\mu)(Y_{t-k}-\mu)]+\beta_2E[(Y_{t-2} -\mu)(Y_{t-k}-\mu)]+\cdots+\beta_pE[(Y_{t-p} -\mu)(Y_{t-k}-\mu)] \\ &= \beta_1\gamma(k-1) + \beta_2 \gamma(k-2) +\cdots+ \beta_p\gamma(k-p) \end{align}$$ 因此，我們可得 $p$ 條方程式：(註：$\gamma(k)=\gamma(-k)$) $$\begin{align} \gamma(1)&= \beta_1\gamma(0) + \beta_2 \gamma(1) +\cdots+ \beta_p\gamma(p-1)\\ \gamma(2)&= \beta_1\gamma(1)+\beta_2 \gamma(2) + \cdots + \beta_p \gamma(p-2) \\ & \vdots \\ \gamma(p)&= \beta_1\gamma(p-1)+ \beta_2 \gamma(p-2) +\cdots+ \beta_p\gamma(0) \end{align}$$ 此外，對於 AR\(p) 的**變異數**根據同樣計算邏輯所得出之結果如下： $$Var(Y_t)=\gamma(0)=\beta_1\gamma(1) + \beta_2 \gamma(2) +\cdots+ \beta_p\gamma(p) + \sigma^2$$ 接著，我們對此 $p$ 條方程式，除上 $\gamma(0)$，將自我共變數轉為自我相關係數： $$\begin{align} \rho(1)&= \beta_1\times1 + \beta_2 \rho(1) +\cdots+ \beta_p\rho(p-1)\\ \rho(2)&= \beta_1\rho(1)+\beta_2 \rho(2) + \cdots + \beta_p \rho(p-2) \\ & \vdots \\ \rho(p)&= \beta_1\rho(p-1)+ \beta_2 \rho(p-2) +\cdots+ \beta_p\times1 \end{align}$$ 這裏我們希望能「**求解**」方程式內 $p$ 個未知的自我相關係數，同時也有 $p$ 條等式，此即 **Yule-Walker 方程式**。在得到各階自我相關係數後，可反推 **AR\(p)** 之**變異數**： $$\gamma(0) = \frac{\sigma^2}{1-\beta_1\rho(1)-\cdots-\beta_p\rho(p)}$$ # 5.3 衝擊反應函數 ## 5.3.1 從 MA(∞) 看衝擊反應函數衝擊反應函數 (Impulse Response Functions，IRF)，指一個時間序列過程面對到隨機衝擊 (外生衝擊) 時，對未來之序列造成之影響。換句話來說，若今日時間序列 $\{Y_t\}$ 面對到隨機衝擊 $e_t$，那衝擊反應函數就是討論 $e_t$ 對 $Y_{t+1}$、$Y_{t+2}$ ⋯⋯ 等的影響。讓我們先看到一個標準的 MA(∞) 模型： $$Y_t =\mu + \sum_{j=0}^\infty \theta_j e_{t-j} = \mu + \theta_0e_t + \theta_1e_{t-1}+ \theta_2e_{t-2}\cdots$$ 因此，若我們想要討論 $e_t$ 對 $Y_{t+j}$ 所造成的影響，需要將 MA(∞) 寫成以 $Y_{t+j}$ 為準的形式： $$Y_{t+j} = \mu + \theta_0e_{t+j} + \theta_1e_{t+j-1}+ \theta_2e_{t+j-2}\cdots+\color{red}{\theta_je_t}+\cdots$$ 所以在此情況下的 **IRF** 為： $$\Psi(j) = \frac{\partial }{\partial e_t} Y_{t+j} = \theta_j$$ $\Psi(j)$ 的值表示若隨機衝擊 $e_t=1$ 對 $Y_{t+j}$ 會有多大的影響。這其實就是一連串「過去」的隨機衝擊的和，並且使用偏微分的方式去計算其影響程度罷了。 :::info 📖 註：$\frac{\partial }{\partial e_t} Y_{t+j} = \theta_j =\frac{\partial }{\partial e_{t-j}} Y_{t}$，因為是在相同的 **DGP** 之下。 ::: ## 5.3.2 AR(1) 的衝擊反應函數對於一個 AR(1) 模型，我們可以將其寫成 MA(∞) 的形式： $$\begin{align} Y_t = \sum_{k=0}^\infty \beta_1^k \beta_o + \underbrace{\sum_{k=0}^\infty \beta_1^k e_{t-k} }_{\text{MA}(\infty) \text{ process}}+ \lim_{n \to \infty} \beta_1^{n+1}Y_{t-(n+1)} \end{align}$$ 同理，對於 $Y_{t+j}$ 可得： $$Y_{t+j} = \sum_{k=0}^\infty \beta_1^k \beta_o + \underbrace{\sum_{k=0}^\infty \beta_1^k e_{\color{red}{t+j}-k} }_{\text{MA}(\infty) \text{ process}}+ \lim_{n \to \infty} \beta_1^{n+1}Y_{t-(n+1)} $$ 因此 AR(1) 的衝擊反應函數 IRF 即為： $$\Psi(j) = \frac{\partial }{\partial e_t} Y_{t+j} = \beta_1^j$$ 繼續討論 AR(1) 的衝擊反應函數 $\Psi(j)$，可以發現該 IRF 的值會和 $\beta_1$ 的取值息息相關。因此，我們可以將 $\beta_1$ 的取值分為以下幾個部分來做研究： 1. $\beta_1 \in (0,1)$ 2. $\beta_1 \in (-1,0)$ 3. $\beta_1 >1$ 4. $\beta_1 <-1$ 以下我們將用 `R` 語言去模擬 AR(1) 模型的衝擊反應函數，其對應的 $\beta_1$ 取值為 0.75、-0.75、1.5 與 -1.5。 - **程式碼** ``` Input: # e_t = 1，並隨後各生成 20 個IRF點 t <- c(0:20) #power = 0~20 #IRF a <- 0.75^t b <-(-0.75)^t c <- 1.5^t d <- (-1.5)^t #plot par(mfrow=c(2,2)) plot(a,type = 'l',ylim = c(0,0.8),xlab = "t",main = expression(beta[1] == 0.75)) plot(b,type = 'l',xlab = "t",main = expression(beta[1] == -0.75)) plot(c,type = 'l',xlab = "t",main = expression(beta[1] == 1.5)) plot(d,type = 'l',xlab = "t",main = expression(beta[1] == -1.5)) ``` ``` Output: ``` ![IRF](https://raw.githubusercontent.com/wwwh0225/bayes_test/main/IRF.png) 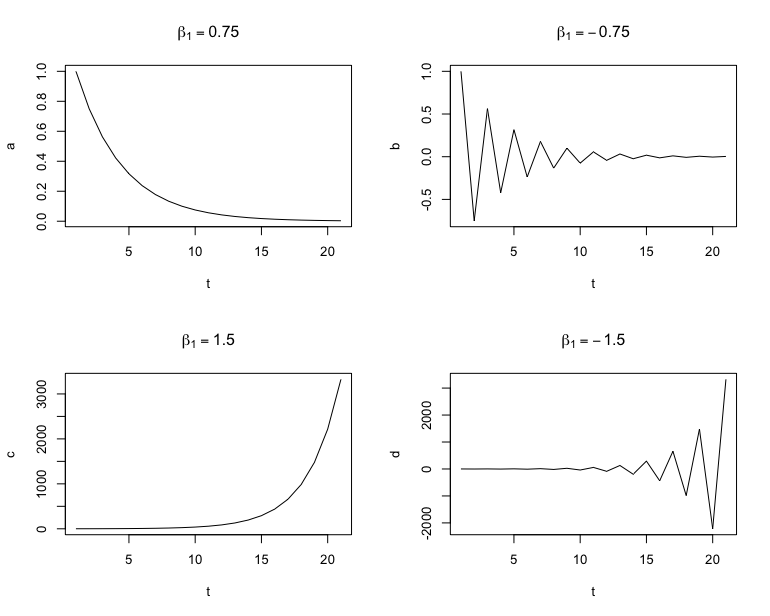很明顯地可以從上圖看出，當 $|\beta_1| \in (0,1)$ 時，衝擊反應函數會收斂，表示隨著時間增加，該衝擊對於時間序列的影響力逐步減小。反之，若 $|\beta_1| > 1$ 時，則該時間序列會發散，因為對於 $e_t=1$ 的衝擊會越來越被放大。此外，當 $\beta_1$ 為**負數**時，衝擊反應函數會隨時間正負擺盪著收斂或是發散。我們也可以比較不同 $\beta_1$ 係數的收斂速度，直觀來說，當 $\beta_1$ 越靠近 1，其 IRF 的收斂會越慢。 :::success 💡 **半衰期 (half-life)** 當時間序列為定態，對於外生衝擊 $e_t=1$ 的影響會隨著時間逐步收斂，當此衝擊減為初始之「**一半**」之時，所經過的時間稱之為「**半衰期**」。對於「半衰期」，我們可以透過衝擊反應函數去求出：若令 $\tau$ 為半衰期，則 $$\tau = \frac{\ln 0.5}{\ln \beta_1}$$ 因為，$\Psi(\tau) = \beta_1^\tau =0.5$ ::: ## 5.3.3 AR\(p) 的衝擊反應函數以下是一個對 **AR\(p)** 模型的基本設定： $$\begin{align} Y_t &= \beta_0 + \beta_1 Y_{t-1} + \beta_2 Y_{t-2}+\cdots+\beta_p Y_{t-p} +e_t \end{align}$$ 根據這個 DGP，只要我們有前 p 期的資訊，再加上本期的隨機衝擊，那就會是本期 ($T = t$) 的取值。而因為 **IRF** 是探討當期的衝擊之於未來序列的影響，因此我們可以反覆代入 AR\(p) 的模型設定，來觀察 $e_t$ 所造成的隨機衝擊對 $Y_{t+j}$ 的數值有多少影響。 $$\begin{align} Y_{t+1} &= \beta_0 + \beta_1\color{red}{ Y_{t}} + \beta_2 Y_{t-1}+\cdots+\beta_p Y_{t-(p-1)} +e_t \\ \vdots \\ Y_{t+j} &= \cdots + \Psi(j) e_t+\cdots \end{align}$$ 因此，為了求出 $Y_{t+j}$ 我們可以將 AR\(p) 寫成「伴隨形式(companion form)」表示： $$ \left[ \begin{matrix} Y_t \\ Y_{t-1} \\ \vdots \\ Y_{t-p+1} \\ \end{matrix} \right]_{p \times 1} = \left[ \begin{matrix} \beta_1 & \beta_2 & \cdots & \beta_{p-1} & \beta_p \\ 1 & 0 & \cdots & 0 & 0 \\ 0 & 1 & \cdots & 0 & 0 \\ \vdots & & \ddots &\vdots & \vdots \\ 0 & 0 & \cdots & 1 & 0\\ \end{matrix} \right]_{p \times p} \left[ \begin{matrix} Y_{t-1} \\ Y_{t-2} \\ \vdots \\ Y_{t-p} \\ \end{matrix} \right]_{p \times 1} + \left[ \begin{matrix} e_t \\ 0 \\ \vdots \\ 0 \\ \end{matrix} \right]_{p \times 1} $$ 為求簡潔，我們可以將其化簡成以下對應的表達式： $$\mathbf{Y}_t =\mathbf{\Phi} \mathbf{Y}_{t-1} + {e}_t$$ 透過上式，我們可以疊代出 $e_t$ 對 $j$ 其後所造成的影響為何，也就是 $\mathbf{\Phi}^j$。由於 $\mathbf{\Phi}_{p\times p}$ 基本上會是一個**滿秩 (full rank)** 的 p 階方陣，因此可對其進行**對角化**，求出衝擊反應函數的解析解。 - $\mathbf{\Phi}$ 的對角化：$\mathbf{\Phi} = U\Lambda U^{-1}$ 其中，$\Lambda$ 為由 $\mathbf{\Phi}$ 之特徵值所組成之**對角矩陣**，$U$ 為與 $\Lambda$ 中對應之特徵值之特徵向量。 :::info 📖 關於矩陣之對角化，詳見：線代啟示錄〈[**可對角化矩陣的譜分解**](https://ccjou.wordpress.com/2010/08/23/%e5%8f%af%e5%b0%8d%e8%a7%92%e5%8c%96%e7%9f%a9%e9%99%a3%e7%9a%84%e8%ad%9c%e5%88%86%e8%a7%a3/)〉。 ::: 故 $\mathbf{\Phi}^j = U\Lambda^j U^{-1}$，而在 $j$ 期後，衝擊 $e_t$ 會受到 $\mathbf{\Phi}^j$ 的影響，因此可得 **AR\(p)** 的**衝擊反應函數 (IRF)** 為當衝擊 $e_t=1$ 時，對第 $t+j$ 期所形成之影響，因此： $$\begin{align} {\Psi}(j) &=\left[ \begin{matrix} 1 &0& \cdots &0\\ \end{matrix} \right]_{1 \times p}\mathbf{\Phi}^j e_t \\ &=\left[ \begin{matrix} 1 &0& \cdots &0\\ \end{matrix} \right]_{1 \times p}\mathbf{\Phi}^j \left[ \begin{matrix} 1 \\ 0 \\ \vdots \\ 0 \\ \end{matrix} \right]_{p \times 1} \\ &= [\mathbf{\Phi}^j]_{11} \end{align}$$ # 5.4 AR 與 MA 相互的對偶關係本節，我們想要來探討 AR($p$) 與 MA($q$) 的對偶性，而在先前的 [5.1.1](https://hackmd.io/EpWUlGerSsG5-_CbM3cmnQ#511-%E4%BD%95%E7%82%BA-AR1) 小節中，得知我們可以用 MA(∞) 去逼近 AR(1)。而另一方面，我們也可以用 AR(∞) 去逼近 MA(1)，此即 AR($p$) 與 MA($q$) 的**對偶 (duality)** 關係。本節，我們將對此部分進行簡易的說明。對於一個 **MA(1)** 模型，我們可以寫成以下形式： $$\begin{align} Y_t &= \mu + e_t - \theta_1 e_{t-1} \\ &= \mu + (1-\theta_1L)e_{t-1} \\ \Rightarrow &(Y_t-\mu)=(1-\theta_1L)e_{t} \\ \Rightarrow &(1-\theta_1L)^{-1}(Y_t-\mu)=e_{t} \end{align}$$ 若 $|\theta|<1$ 則， $$\begin{align} &(1-\theta_1L)^{-1}(Y_t-\mu)=e_{t}\\ \Rightarrow & (1-\theta_1L)^{-1}Y_t - \underbrace{(1-\theta_1L)^{-1}\mu }_{=\tilde{\mu}}= e_{t} \\ \Rightarrow &(1+\theta_1L + \theta_1^2 L^2+\cdots)Y_t-\tilde{\mu}=e_{t}\\ \Rightarrow &(Y_t +\theta_1Y_{t-1} + \theta_1^2 Y_{t-2}+\cdots) -\tilde{\mu}=e_{t} \\ \Rightarrow & Y_t = \tilde{\mu} + [(-\theta_1)Y_{t-1}+(-\theta_1^2)Y_{t-2}+(-\theta_1^3)Y_{t-2}+\cdots) ]+e_t \end{align}$$ 此即一個 **AR(∞)** 模型。 # 5.5 AR\(p) 在 R 中的模擬透過 `R` 語言，我們能輕易地對 AR 模型進行模擬，而透過模擬的資料，能讓我們對實證上的 AR 模型有更深的認識，進而了解其性質。 ## 5.5.1 偏自我相關函數在 [**Ch4**](https://hackmd.io/@wwwh0225/r1B6F8JBA#422-%E7%A7%BB%E5%8B%95%E5%B9%B3%E5%9D%87%E6%A8%A1%E5%9E%8B) 中，我們曾介紹 **MA(q)** 模型的自我相關函數 (ACF)，當 ACF 之階數大於 q 時，對應之 ACF 值會為 0。透過此性質，我們可以在實證上對一個 MA(q) 模型進行對 q 的**定階**。同樣地，我們也會想找一個能對 **AR\(p)** 定階的方法，我們在此介紹「**偏自我相關函數 (partial autocorrelation function，PACF)**」。(詳見：[此連結](http://sfb649.wiwi.hu-berlin.de/fedc_homepage/xplore/tutorials/sfehtmlnode59.html)或銀慶剛老師[講義](https://mx.nthu.edu.tw/~cking/courses/analysis_of_depedent_data/acf_pacf.pdf)) 由於推導 PACF 較為繁複，我們在此不提，但 PACF 基本上是一種「在其他條件不變」之下的相關係數。若我們令 $\phi_k$ 為 $k$ 階 PACF，則： $$\begin{align} \phi_1 &= \rho(1)\\ \phi_2 &= \dfrac{\text{Covariance}(x_t, x_{t-2}| x_{t-1})}{\sqrt{\text{Variance}(x_t|x_{t-1})\text{Variance}(x_{t-2}|x_{t-1})}}\\ \phi_3 &= \dfrac{\text{Covariance}(x_t, x_{t-3}| x_{t-1}, x_{t-2})}{\sqrt{\text{Variance}(x_t|x_{t-1},x_{t-2})\text{Variance}(x_{t-3}|x_{t-1},x_{t-2})}} \end{align}$$ 以此類推。直觀上來說，我們可以透過資料建立以下**最佳線性預測式 (best linear predictor)**： $$\hat{Y_t} = \alpha_0 + \alpha_1 Y_{t-1}+ \alpha_2 Y_{t-2}+ \cdots $$ 這其實就是一個 AR\(p) 模型的估計。其中，$\alpha_1$ 即為在其他項（$Y_{t-2}$、$Y_{t-3}$、⋯）不變的情況下，$Y_{t-1}$ 對 $Y_{t}$ 的影響。若兩者相關性為 0，則 $\alpha_1$ 應為 0，而這也就是 PACF 的觀念。因此，若 AR\(p) 模型是我們資料的 DGP，則其 PACF 應**顯著異於 0**。 :::info 📖 當 AR 或 MA 的落後期並非連續，或為混合的 ARMA 模型，則在使用 ACF 或 PACF 判斷落後期數時，可能會有偏誤。詳見：[楊奕農（2017）](https://www.eslite.com/product/1001130482580209?utm_content=&gad_source=1&gclid=Cj0KCQjwv7O0BhDwARIsAC0sjWNqm6hJ0MzjFhAlFNOoFskV8WDrkh8Xr-YnUzgSu1U8LWnts0THITQaAsDoEALw_wcB)。 ::: ## 5.5.2 模擬 AR(1) 模型若我們考慮一 AR(1) 模型： $$Y_t = 0.85 Y_{t-1} + e_t$$ 其中，$e_t \overset{i.i.d.}{\sim} N(0,1)$ AR(1) 在理論上的動差為： $$\begin{align} E[Y_t] &= \frac{\beta_0}{1-\beta_1} = 0\\ Var[Y_t] &= \frac{\sigma^2}{1-\beta_1^2} = \frac{1^2}{1-0.85^2} = 3.60 \\ \gamma(1) &= \beta_1 \gamma(0) = 3.06 \\ \rho(1) &= \beta_1 = 0.85 \end{align}$$ 讓我們用 `R` 去生成此 AR(1) 模型的 150 個資料點： ``` Input: set.seed(9527) # 生成 AR(1) 的資料, beta1 = 0.85 的模型，預設的白噪音 error 是標準常態 Yt <- arima.sim(n=150, list(ar=c(0.85))) # 匯出生成點們 print(Yt) ``` ``` Output: Time Series: Start = 1 End = 150 Frequency = 1 [1] -0.65509969 0.31476229 0.80808844 0.99835478 -0.42929245 [6] 0.38297921 0.02329217 -1.11623670 -2.12014595 -2.61662343 [11] -1.85697710 -0.91517749 -1.11316100 -0.72853924 -1.45275658 [16] -1.28312170 -1.28689183 -1.07047246 -0.29767562 -0.19719168 [21] -0.68859658 -0.66242823 -2.42850639 -0.98501368 -0.08200923 [26] 0.02908906 -1.59324210 -1.78801271 -0.92355053 -1.23559571 [31] 0.91991834 0.19830531 0.29122906 -0.74670192 -0.74682227 [36] -1.66393808 -2.99217328 -2.36172904 -2.98992361 -1.88704809 [41] -2.05344850 -1.58700388 -2.46668664 -0.66513577 0.41441050 [46] 0.27803411 -0.38710479 -0.12561650 3.11906771 3.19314106 [51] 0.71937775 2.67226853 1.28675412 -1.27248045 -1.58027995 [56] -1.12405192 -2.78413692 -1.87552815 -1.64335485 -1.84194662 [61] -1.99084753 -3.76786927 -4.02802130 -4.76681478 -5.92446796 [66] -3.72691346 -3.84459318 -3.18832333 -1.08669648 0.28248065 [71] 1.26392326 2.51385982 2.79924952 2.75006171 1.69467932 [76] 3.19421965 2.57233802 2.12289430 1.78390351 0.15354532 [81] -0.20366226 0.48733085 -1.23510927 -1.14987881 -1.28377384 [86] -0.13124765 0.03806370 0.88314355 2.09979420 4.69219930 [91] 3.63662332 3.03612566 0.65124970 -0.04337197 0.13703843 [96] 0.41876590 1.98037681 0.63600454 -0.44535211 -0.16789253 [101] -0.55143278 -0.54895760 0.76159112 -0.64020917 0.17965701 [106] -1.20483520 -1.41146971 -1.45683933 -1.33968543 -2.07564923 [111] 0.16703813 0.18127104 0.87401180 0.17465794 -1.05264487 [116] -0.55101119 0.43659700 -0.60243005 0.53084677 0.56813475 [121] 2.07202762 3.25284436 1.45870657 1.10959973 2.90478316 [126] 3.11248534 1.53326164 0.95115884 -0.19906737 -0.44027893 [131] 0.67609987 0.97518477 -0.22529764 -1.49649898 -0.72465098 [136] -0.29070095 0.27721083 0.48859118 0.66770380 3.35986041 [141] 3.35480388 1.63512428 1.95203200 0.96287062 1.57997530 [146] 2.02361712 2.44297221 2.87176512 3.31948398 3.91571989 ``` ``` Input: # 繪圖看看走勢 plot(Yt,main = "AR(1) beta_1 = 0.85") abline(h=0,lty=3) ``` ``` Output: ``` ![AR1_line](https://hackmd.io/_uploads/SkBQXliPA.png) **計算樣本動差：** ``` Input: #平均數: mean(Yt) #變異數 var(Yt) ``` ``` Output: #平均數: [1] -0.03912862 #變異數 [1] 3.506367 ``` ``` Input: #一階自我共變異數 ACVF ACVF <- acf(Yt,type = "covariance", xlim=c(1,10), main="ACVF for simulated AR(1)",plot = T) text(x = 1.5, y =ACVF$acf[2], labels = as.character(round(ACVF$acf[2],4))) ``` ``` Output: ``` ![AR1_ACV](https://hackmd.io/_uploads/H1j-VgowA.png) ``` Input: # 一階自我相關係數 ACF ACF <- acf(Yt,type = "correlation", xlim=c(1,10), main="ACF for simulated AR(1)",plot = T) text(x = 1.5, y =ACF$acf[2], labels = as.character(round(ACF$acf[2],4))) ``` ``` Output: ``` ![AR1_ACF](https://hackmd.io/_uploads/SyMsEgivR.png) - **PACF** ``` Input: # 一階「偏」自我相關係數 PACF PACF <- acf(Yt,type = "partial", xlim=c(1,10), main="PACF for simulated AR(1)",plot = T) text(x = 1.5, y =PACF$acf[1], labels = as.character(round(PACF$acf[1],4))) text(x = 2.5, y =PACF$acf[2], labels = as.character(round(PACF$acf[2],4))) ``` ``` Output: ``` ![AR1_PACF](https://hackmd.io/_uploads/rJmirgjw0.png) - **理論值與模擬值 (n=150) 的比較** | 動差 | 理論值 | 模擬值 | | ------------------ | -------- | -------- | | 均數 | 0 | -0.0391 | | 變異數 | 3.60 | 3.5063 | | 一階自我共變數 | 3.06 | 2.8526 | | 一階自我相關係數 | 0.85 | 0.819 | | 一階自我**偏**相關係數| 0.85 | 0.819 | | 二階自我**偏**相關係數 | 0 | -0.0511 | ## 5.5.3 模擬 AR(3) 模型若我們考慮一 AR(3) 模型： $$Y_t = 0.7 Y_{t-1}+0.25Y_{t-2} -0.175Y_{t-3} + e_t$$ 其中，$e_t \overset{i.i.d.}{\sim} N(0,1)$ AR(3) 在理論上的均數為： $$E[Y_t]=\mu = \frac{0}{1-0.7-0.25+0.175}=0$$ 而其對應之 $k$ 階自我共變異數 ($k = 0,1,2,\cdots$) 會需要透過 Yule-Walker 方程式來求出，由於計算上有些複雜，在此我們直接使用 `R` 中的套件 `ltsa` 來協助我們進行計算。若先前無下載此套件，請先在 `R` 中執行： ``` Input: install.packages("ltsa") ``` 此指令會在 `R` 中下載對應之套件。接著使用 `library()` 函數來叫出對應的套件： ``` Input: library(ltsa) ``` - k 階自我共變異數 (ACVF) 理論值 ``` Input: acvf <- tacvfARMA(phi =c(0.7,0.25,-0.175), #AR coefficient theta = numeric(0), #MA coefficient maxLag = 10, sigma2 = 1) print(acvf) ``` ``` Output: [1] 2.6754557 2.0855446 1.7637748 1.2878238 0.9774500 0.6975104 [7] 0.5072506 0.3583993 0.2556278 0.1797704 0.1270264 ``` 上列產出之「2.6754557」為 0 階自我共變異數，亦即「自我共變數」，而「2.0855446」為一階自我共變異數，以此類推。同樣地，若我們對於 AR(3) 的「理論」 ACF 有興趣，除了可以使用 ACVF 的數值自行求出，也可以透過 `R` 中內建的函數 ` ARMAacf()` 來求出自我相關函數： - 用 ACVF 來求出 ACF： ``` Input: # 承上之 acvf acf <- acvf/acvf[1] print(acf) ``` ``` Output: [1] 1.00000000 0.77951002 0.65924276 0.48134744 0.36533964 0.26070713 [7] 0.18959410 0.13395821 0.09554553 0.06719245 0.04747841 ``` 得出此 AR(3) 理論上之一階自我相關函數為「0.77951002」、二階自我相關函數為「0.65924276」，以此類推。 - 用 `ARMAacf()` 來求出 ACF： ``` Input: ARMAacf(ar = c(0.7,0.25,-0.175), lag.max = 10, pacf = FALSE) ``` ``` Output: 0 1 2 3 4 5 1.00000000 0.77951002 0.65924276 0.48134744 0.36533964 0.26070713 6 7 8 9 10 0.18959410 0.13395821 0.09554553 0.06719245 0.04747841 ``` 此與使用 ACVF 所求出的結果一致。 - 「理論」偏自我相關函數 PACF 只要將 `ARMAacf()` 設定為 `pacf = TRUE` 即可求出。 ``` Input: ARMAacf(ar = c(0.7,0.25,-0.175), lag.max = 10, pacf = TRUE) ``` ``` [1] 7.795100e-01 1.315280e-01 -1.750000e-01 0.000000e+00 [5] -3.712941e-17 -4.266532e-17 9.171369e-17 -7.111763e-17 [9] -1.873847e-17 9.282352e-18 ``` 我們可以看出對於一個 AR(3) 模型，$\rho(k)$ 在 $k>3$ 時之值為**零** (在電腦運算上存在些許誤差)。我們可以將理論上之 **ACF** 與 **PACF** 用 `R` 畫出，在此介紹另外一個套件 `simts`，其中某些函數能協助我們畫出漂亮的圖形。 ``` Input: library(simts) #呼叫套件 par(mfrow = c(1, 2)) #合併兩張圖 #畫出 ACF 理論值 plot(theo_acf(ar =c(0.7,0.25,-0.175) , ma = NULL, lagmax = 10) ) #畫出 PACF 理論值 plot(theo_pacf(ar =c(0.7,0.25,-0.175) , ma = NULL, lagmax = 10)) ``` ``` Output: ``` ![AR3_threo_ACF_PACF](https://hackmd.io/_uploads/S1K_z61_A.png) 讓我們同樣用 R 去生成此 AR(3) 模型的 150 個資料點： ``` Input: set.seed(9527) # 生成 AR(3) 的資料，預設的白噪音 error 是標準常態 Yt <- arima.sim(n=150, list(ar=c(0.7,0.25,-0.175))) # 匯出生成點們 print(Yt) ``` ``` Output: Time Series: Start = 1 End = 150 Frequency = 1 [1] 2.268699460 1.691952503 1.010859333 -0.393367158 -0.504183440 [6] -2.110002431 -2.110606264 -1.037473528 -1.679147075 -2.758853755 [11] -1.785550553 -2.503677425 -2.548173824 -2.412065567 -2.645376936 [16] -1.430658131 -1.342702163 -2.422206385 -1.601831616 -0.320829210 [21] 0.037303470 -0.009844426 1.565091888 1.294735477 1.116753846 [26] 0.704663368 1.191654443 -0.875583341 0.255513237 0.112376627 [31] -0.082571375 0.972969743 -0.873063095 -0.336741246 0.437230159 [36] 1.176179689 0.992400030 2.049375458 1.333013545 0.400991664 [41] 1.104738730 2.531578737 0.659328782 -0.914874597 0.461443034 [46] -1.651010118 -0.014014939 -2.240680037 -1.389716148 -2.650855781 [51] -0.232614576 -0.825855020 -0.448573172 -0.644879440 0.426292144 [56] 0.550042360 0.250530159 0.020449827 0.235820383 -0.502490388 [61] 1.166441601 0.183621901 0.242387804 0.987871771 2.262128337 [66] 2.121966740 0.858919919 0.487660745 -1.416502802 -0.580925084 [71] -0.005543221 -0.898132999 -0.786538418 -0.650134950 0.236324425 [76] -1.280946259 -2.753888159 -3.572633551 -5.312287375 -5.219372764 [81] -2.581286546 0.858248825 -0.584715201 0.104291885 0.833807675 [86] 0.966237646 0.992213823 1.771531464 -0.379027272 -2.841889430 [91] -1.204537509 -0.827070322 -0.316850061 0.982805229 2.599439422 [96] 2.017540591 1.285866253 1.492273799 1.095607448 1.091938206 [101] 1.478139225 2.019277196 1.352259320 1.533246118 -0.182442224 [106] 0.485365875 0.946158595 2.020696640 1.664035659 1.378660749 [111] 0.811500556 1.281657637 -0.303624161 0.381139168 0.200185234 [116] 1.608305648 2.003402478 2.163284615 3.744067093 3.300140522 [121] 2.485643579 3.345967881 2.267055136 3.467373239 2.035129241 [126] 0.660832634 0.468663829 -0.744741549 -0.825774055 -0.586951290 [131] 0.323678198 3.147043346 2.363430106 1.738186011 2.518438856 [136] 3.714042502 2.333844101 2.354965291 0.548846448 -1.290424654 [141] -0.287878479 -0.138191459 -0.546238871 -1.495713671 -1.008226004 [146] -1.175616943 -1.277524018 -0.217744408 0.467253347 0.292454209 ``` 同樣地，讓我們將此 AR(3) 模型畫出來看一下趨勢： ``` Input: # 繪圖看看走勢 plot(Yt,main = expression( paste("AR(3):", Y[t] == 0.7 *Y[t-1]+ 0.25 *Y[t-2] - 0.175 *Y[t-3] + e[t] ) )) abline(h=0,lty=3) ``` ``` Output: ``` ![AR3_line](https://hackmd.io/_uploads/rkCTuTJOC.png) **計算樣本動差：** ``` Input: #平均數: mean(Yt) #變異數 var(Yt) ``` ``` Output: #平均數: [1] 0.1853469 #變異數 [1] 2.738685 ``` ``` Input: #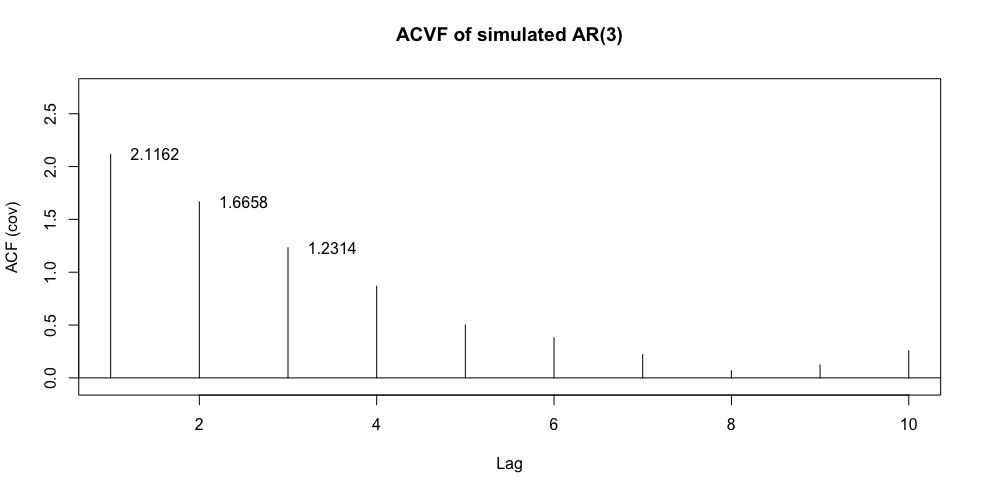自我共變異數 ACVF ACVF <- acf(Yt,type = "covariance", xlim=c(1,10), main="ACVF of simulated AR(3)",plot = T) text(x = 1.5, y =ACVF$acf[2], labels = as.character(round(ACVF$acf[2],4))) text(x = 2.5, y =ACVF$acf[3], labels = as.character(round(ACVF$acf[3],4))) text(x = 3.5, y =ACVF$acf[4], labels = as.character(round(ACVF$acf[4],4))) ``` ``` Output: ``` ![AR3_ACV](https://ppt.cc/fd6D6x@.png) ``` Input: # 自我相關函數 ACF ACF <- acf(Yt,type = "correlation", xlim=c(1,10), main="ACF of simulated AR(3)",plot = T) text(x = 1.5, y =ACF$acf[2], labels = as.character(round(ACF$acf[2],4))) text(x = 2.5, y =ACF$acf[3], labels = as.character(round(ACF$acf[3],4))) text(x = 3.5, y =ACF$acf[4], labels = as.character(round(ACF$acf[4],4))) ``` ``` Output: ``` ![AR3_ACF](https://hackmd.io/_uploads/HJvQeAJdC.png) ``` Input: # 自我「偏」相關函數 PACF PACF <- acf(Yt,type = "partial", xlim=c(1,10), main="PACF of simulated AR(3)",plot = T) text(x = 1.5, y =PACF$acf[1], labels = as.character(round(PACF$acf[1],4))) text(x = 2.5, y =PACF$acf[2], labels = as.character(round(PACF$acf[2],4))) text(x = 3.5, y =PACF$acf[3], labels = as.character(round(PACF$acf[3],4))) ``` ``` Output: ``` ![AR3_PACF](https://hackmd.io/_uploads/BJ19fC1_C.png) 在此圖可看到 PACF 在二階與三階時沒有超過 95% 的信賴區間，這不符合我們對 PACF 的認識，讓我們將模擬的期數增加到 500 期重新模擬看看。 ![AR3_PACF500](https://hackmd.io/_uploads/r1pU40y_0.png) 當期數變大時，樣本動差會逐步收斂到母體動差。 - **理論值與模擬值 (n=150, n=500) 的比較** | 動差 | 理論值 | 模擬值 (n=150) | 模擬值 (n=500) | | ---------------------- | ------ | --- | ----------- | | 均數 | 0 | 0.1853 | -0.2688 | | 變異數 | 2.6754 | 2.7387 | 3.0824 | | 一階自我共變數 |2.0855 | 2.1162 | 2.4745 | | 一階自我相關係數 | 0.7795 | 0.7779 | 0.8044 | | 二階自我相關係數 | 0.6592 | 0.6123 | 0.6833 | | 三階自我相關係數| 0.4813 | 0.4526 | 0.5082 | | 一階自我**偏**相關係數 | 0.7795 | 0.7779 | 0.8044 | |二階自我**偏**相關係數 | 0.1315 | 0.0182 | 0.1027 | | 三階自我**偏**相關係數 | -0.1750 | -0.0739 | -0.1933 | # 參考資料 1. 陳旭昇（2022）。《時間序列分析: 總體經濟與財務金融之應用》(3版)。 2. 陳旭昇（2015）。《統計學: 應用與進階》(3版)。 3. 楊奕農（2017）。《時間序列分析: 經濟與財務上之應用》(3版)。 4. 葉小蓁（1998）。《時間序列分析與應用》。 5. [顏國勇（2011）。《機率論》，電子書。](https://library.math.ncku.edu.tw/documents/1/Probability21A.pdf) 6. [北京大學「金融時間序列分析」講義](https://www.math.pku.edu.cn/teachers/lidf/course/fts/ftsnotes/html/_ftsnotes/ftsnotes.pdf)。 7. [北京大學「金融中的随机数学」講義](https://www.math.pku.edu.cn/teachers/lidf/course/stochproc/stochprocnotes/html/_book/index.html)。 8. Klaus Neusser (2015), Time Series Analysis in Economics, Springer. 9. Fumio Hayashi (2000), Econometrics, Princeton University Press. 10. Jonathan D. Cryer and Kung-Sik Chan (2008), Time Series Analysis with Applications in R, Springer. 11. Paul S.P. Cowpertwait and Andrew V. Metcalfe (2009), Introductory Time Series with R, Springer. 12. Walter Enders (2015), Applied Econometric Time Series, Wiley. 13. [Christoph Hanck, Martin Arnold, Alexander Gerber, and Martin Schmelzer(2024), Introduction to Econometrics with R.](https://www.econometrics-with-r.org/index.html) 14. Bruce E. Hansen (2021), Econometrics, Princeton University Press. 15. Steven Shreve (2003), Stochastic Calculus for Finance”, Vol 2, Springer. 16. [Rao, S. S. (2008). A course in time series analysis. In Technical Report. Texas A&M University.](https://web.stat.tamu.edu/~suhasini/teaching673/time_series.pdf)