---
title: 【時間序列分析】Ch6:ARMA 與線性模型之理論基礎
image: https://ppt.cc/flVaux@.jpg
---
# 【時間序列分析】Ch6:ARMA 與線性模型之理論基礎
在時間序列的分析中,我們常使用線性模型去描述隨機過程的走勢。本章將會介紹線性模型之理論基礎以及相當重要的 ARMA 模型。
# 6.1 The Wold Decomposition Theorem
## 6.1.1 投影誤差
如同 OLS 線性迴歸,時間序列的線性模型預測也是一種在超平面上的投影,所展出的超平面是由過往的歷史資料所構築而成。讓我們定義歷史資料的資訊集合為:$\tilde{Y}_{t-1}=\{\cdots,Y_{t-2},Y_{t-1}\}$,並且定義 $Y_t$ 到 $\tilde{Y}_{t-1}$ 所展開的超平面 ([希爾伯特空間](https://zh.wikipedia.org/zh-tw/%E5%B8%8C%E5%B0%94%E4%BC%AF%E7%89%B9%E7%A9%BA%E9%97%B4)) 的「**投影** (Projection)」為:$\mathscr{P}[Y_t|\tilde{Y}_{t-1}]=\mathscr{P}_{t-1}[Y_t]$,其投影誤差是唯一的 $e_t = Y_t - \mathscr{P}_{t-1}[Y_t]$。
對於投影誤差 $e_t$ 有下列性質:
- 均值為 0:$E[e_t]=0$
- 序列無相關:$E[e_t e_{t-j}]=0, \forall j \geq 1$
- 有限變異數:$\sigma^2 =E[e_t^2]\leq E[Y_t^2] < \infty$
同時,若 $\{Y_t\}$ 為嚴格定態,則 $\{e_t\}$ 也為嚴格定態。
:::info
📖 在此處,$\{e_t\}$ 被稱為 **innovation process**,指隨時間加入的「新資訊」與先前的資訊**相互無關**。
:::
## 6.1.2 Wold Decomposition
**Wold Decomposition** 是線性時間序列分析中的一個重要理論,讓我們能夠使用線性模型去對時間序列資料進行近似。該理論指出一個**弱定態**時間序列 $\{Y_t\}$ 可以被拆解成一個「**確定性 (deterministic)**」時間序列和一個「**隨機 (stochastic)**」時間序列的**和**。(證明請見:[Christiano](https://faculty.wcas.northwestern.edu/lchrist/finc520/wold.pdf)。)
對於一個**弱定態**時間序列 $\{Y_t\}$,且其投影誤差之變異數為 $\sigma^2>0$,**Wold Decomposition Theorem** 顯示 $Y_t$ 可以被下列的線性表達式所表示﹔
$$Y_t = \mu_t + \sum_{j=0}^\infty b_j e_{t-j}$$
其中,$e_t$ 為投影誤差。
在此表達式中,第一項 $\mu_t$ 為時間序列中的「**確定性**」部分,而第二項的 $\sum_{j=0}^\infty b_j e_{t-j}$ 即為「**隨機性**」部分,並有以下性質:
- $e_t$ 為白噪音投影誤差:$e_t \equiv Y_t - \mathscr{P}_{t-1}[Y_t]$
- $\mu_t$ 為 $Y_t$ 到過往歷史資料 ($\tilde{Y}_{t-m}=\{Y_{t-m},Y_{t-(m-1)},\cdots\}$) 上的投影:$\mu_t \equiv \lim_{m \to \infty}\mathscr{P}_{t-m}[Y_t]$,表示只要知道過去的歷史資料,本期資料是「完全可以」被預測的。這裡指的是此部分的隨機性質是確定的,訊息量並沒有隨著時間而改變。
- $\sum_{j=0}^\infty b_j e_{t-j}$ 是無窮多項白噪音的和,通常會設定 $e_t \sim WN(0,\sigma^2)$、$b_0 =1$ 與 $\sum_{j=1}^\infty b_j^2 < \infty$ (square summable),而這也就是一個 **MA** 過程。
:::success
💡 當 $\mu_t$ 為一個常數,則我們稱時間序列 $\{Y_t\}$ 為「非確定性 (non-determinstic)」時間序列。亦即
$$Y_t = \mu + \sum_{j=0}^\infty b_j e_{t-j}$$
對於確定性與非確定性過程,可詳閱:[**Ruhm(2008)**](https://www.researchgate.net/profile/Karl-Ruhm/publication/265275896_Deterministic_Nondeterministic_Signals/links/54d9f32e0cf24647581fde53/Deterministic-Nondeterministic-Signals.pdf)。
:::
## 6.1.3 Autoregressive Wold Representation
對於一個隨機過程而言,若將其進行 Wold decomposition 則只會有一個「唯一」的表示方法。透過 MA 模型的可逆性,我們也可以將 Wold decomposition 轉為 **AR** 的方式作為表示。
$$\begin{align}
Y_t &= \mu + \sum_{j=0}^\infty b_j e_{t-j} \\
&= \mu + (b_0+b_1L+b_2 L^2+\cdots)e_t \\
&= \mu + b(L)e_t \\
\Rightarrow & Y_t -\mu = b(L)e_t \\
\Rightarrow & b(L)^{-1}(Y_t -\mu) =e_t \\
\Rightarrow & b(L)^{-1}Y_t -b(L)^{-1}\mu = e_t\\
\Rightarrow & b(L)^{-1}Y_t = \underbrace{\tilde{\mu}}_{b(L)^{-1}\mu} +e_t
\end{align}$$
又因為 $b(L)$ 可逆,亦即 $b(z)$ 之根都落在單位圓之外,因此 $b(L)^{-1}$ 也是一個落後多項式 (lag polynomial):
$$b(L)^{-1} = 1 - a_1L -a_2 L^2-\cdots$$
因此:
$$\begin{align}
&b(L)^{-1}Y_t = {\tilde{\mu}}+e_t \\
&\Rightarrow (1 - a_1L -a_2 L^2-\cdots)Y_t = {\tilde{\mu}}+e_t \\
&\Rightarrow Y_t -a_1Y_{t-1}-a_2Y_{t-2}-\cdots = {\tilde{\mu}}+e_t \\
&\Rightarrow Y_t = (a_1Y_{t-1}+a_2Y_{t-2}+\cdots) +{\tilde{\mu}}+e_t \\
&\Rightarrow Y_t = \tilde{\mu} + \sum_{j=1}^\infty a_jY_{t-j} + e_t
\end{align}$$
自此,我們認識到一個弱定態時間序列可以表示成 **MA** 的形式,也可以表示成 **AR** 的形式。若我們將時間序列的線性表示做更寬鬆的表示,則可以結合 AR 模型與 MA 模型,成為 **ARMA** 模型,使得 AR、MA 都是 ARMA 模型中的一個特例,而這會是對 Wold representation 的一個良好近似。
# 6.2 ARMA 模型
正如先前所提到的,對於一個時間序列 $\{Y_t\}$,我們可以將 AR\(p) 以及 MA(q) 模型結合,形成一個更為一般化的模型 **ARMA(p,q)**。其中 AR\(p) 模型即為 ARMA(p,0),而 MA(q) 為 ARMA(0,q)。
## 6.2.1 ARMA 模型與 Wold Representation
對於一個 **ARMA(p,q)** 模型,我們可以有以下的模型設定:
$$Y_t = \beta_0 + \beta_1 Y_{t-1} + \beta_2 Y_{t-2}+\cdots+\beta_p Y_{t-p} + e_t + \theta_1e_{t-1} +\theta_2 e_{t-2}+\cdots + \theta_qe_{t-q}$$
其中 $\{e_t\}$ 是嚴格定態且具遍歷性的白噪音過程。
如同先前對模型的分析,我們同樣可以將 ARMA 模型以落後運算元的方式進行改寫:
$$\beta(L)Y_t = \beta_0 + \theta(L)e_t$$
其中:
$$\begin{align}
\beta(L) &= 1-\beta_1L -\beta_2L^2-\cdots-\beta_pL^p \\
\theta(L) &= 1+ \theta_1L + \theta_2L^2 + \cdots + \theta_qL^q
\end{align}$$
若 $\beta(z)$ 的根都落在單位圓之外,也就是說 $\beta(L)$ 可逆,此時:
$$Y_t = \beta(L)^{-1}(\beta_0 + \theta(L)e_t)=\beta(L)^{-1}\beta_0 +\frac{\theta(L)}{\beta(L)}e_t$$
若我們令 $\mu = \beta(L)^{-1}\beta_0$ 且 $b(L)=\frac{\theta(L)}{\beta(L)}$,則 ARMA 模型即可轉為 **Wold representation** 的形式:$Y_t=\mu+b(L)e_t$
由於 $\{e_t\}$ 為定態時間序列,透過 $\beta(L)$ **可逆**的條件,可以將 ARMA 模型寫成一連串 MA 序列 ($\{e_t\}$) 的線性組合,也就是說 $\{Y_t\}$ 也是一個**定態**時間序列。
:::info
📖 當一個 ARMA(p,q) 過程 $\{Y_t\}$ (demeaned) 可以被表示為:
$$Y_t = \sum_{j=0}^\infty \psi_j e_{t-j}$$
同時 $\sum_{j=0}^\infty|\psi_j|<\infty$。
則我們稱 ARMA(p,q) 過程 $\{Y_t\}$ 具有因果性 (**causal**),或稱其為 $\{e_t\}$ 的因果函數 (**casual function**)。
:::
## 6.2.2 ARMA 模型的可逆性
為求簡化,讓我們考慮一個去除均數 (demeaned) 的 ARMA 模型:
$$\beta(L)Y_t = \theta(L)e_t$$
若一個 ARMA(p,q) 過程 $\{Y_t\}$ 可以被表示成:
$$e_t = \sum_{j=0}^\infty \pi_j Y_{t-j}$$
且 $\sum_{j=0}^\infty|\pi_j|<\infty$,則稱此 ARMA(p,q) 模型**可逆 (invertible)**。
:::success
💡 **ARMA 的可逆條件**
若 $\theta(z)$ 的根都落在單位圓之外,則
$$\begin{align} &\underbrace{\theta(L)^{-1}\beta(L)}_{\pi(L)}Y_t = e_t \\
& \Rightarrow \pi(L)Y_t=e_t
\end{align}$$
其中,$\pi(L) = (1-\pi_1L-\pi_2L^2-\cdots)$
此即 ARMA 之可逆條件。我們並可進一步將 ARMA(p,q) 寫成 AR(∞):
$Y_t = e_t +\pi_1 Y_{t-1} +\pi_2 Y_{t-2}+\cdots$
:::
## 6.2.3 ARMA(1,1) 模型的動差性質
對於一個 **ARMA(1,1)** 模型,我們可以有下列表示:
$$Y_t = \beta_0 + \beta_1 Y_{t-1} + e_t +\theta_1 e_{t-1}$$
其中,$\{e_t\} \sim WN(0,\sigma^2)$。
若將其以落後運算元表示,則為:
$(1-\beta_1L)Y_t= \beta_0 + (1+\theta_1 L)e_t$
在 ARMA(1,1) 的模型中,若 $|\beta_1|<1$ 則此時間序列為**定態**;若 $|\theta_1|<1$ 則表示此時間序列**可逆**。而為了使 ARMA(1,1) 有意義,我們也同時要求 $-\beta_1 \neq \theta_1$,否則模型會退化成白噪音。
接下來,我們便可以討論「定態」 ARMA(1,1) 的**動差**性質:
- **均數 Mean**
對 ARMA(1,1) 模型取期望值,並且使用定態條件:
$$ \begin{align}
& \underbrace{E[Y_t]}_\mu = \beta_0 + \beta_1 \underbrace{E[Y_{t-1}]}_{\mu} +\underbrace {E[ e_t] +\theta_1 E[e_{t-1}]}_{0} \\
& \mu = \beta_0 + \beta_1 \mu \quad \Rightarrow \mu = \frac{\beta_0}{1-\beta_1}
\end{align}$$
此結果與 AR(1) 的均數一致。
- **變異數 Variance**
為求計算簡便,我們在此令 $\beta_0 = 0$,常數的數值變化並不會影響變異數的結果。
根據定態的性質:$Var[Y_t] = Var[Y_{t-1}]$ 、$Var[e_t] = Var[e_{t-1}]=\sigma^2$。
$$ \begin{align}
Var[Y_t] &= \beta_1^2Var[ Y_{t-1}] + Var[e_t] +\theta_1^2 Var[ e_{t-1}] \\
&+ \underbrace{ 2\beta_1 Var[Y_{t-1}e_t] + 2\theta_1 Var[e_t e_{t-1}]}_{0} + 2\beta_1 \theta_1 E[Y_{t-1}e_{t-1}] \\
&= \beta_1^2Var[ Y_{t}] + (1+\theta_1^2) \sigma^2 + 2\beta_1 \theta_1 E[Y_{t-1}e_{t-1}]
\end{align}$$
接續上式,我們需要計算 $E[Y_{t-1}e_{t-1}]$,透過對ARMA(1,1) 模型乘上其誤差項,可得:
$$Y_t e_t = \beta_1 Y_{t-1} e_t + e_t^2 +\theta_1 e_t e_{t-1}$$
對其再取期望值:
$$E[Y_t e_t ]= \underbrace{ \beta_1 E[Y_{t-1} e_t]}_{0} +\underbrace{ E[e_t^2 ]}_{\sigma^2} +\underbrace{ \theta_1 E[e_t e_{t-1}] }_0 = \sigma^2$$
此結果對所有 $t$ 皆成立。
因此,
$$ \begin{align}
& Var[Y_t] = \beta_1^2Var[ Y_{t}] + (1+\theta_1^2) \sigma^2 + 2\beta_1 \theta_1 \underbrace{ E[Y_{t-1}e_{t-1}]}_{\sigma^2} \\
& (1-\beta_1^2)Var[Y_t] =(1+\theta_1^2 + 2\beta_1 \theta_1 ) \sigma^2 \\
& \Rightarrow Var[Y_t] =\frac{(1+\theta_1^2 + 2\beta_1 \theta_1 ) \sigma^2 }{1-\beta_1^2}
\end{align}$$
由於變異數**必正**,因此我們必須要求 $\beta_1^2 <1$,也就是 $|\beta_1|<1$,此與先前設定之定態條件一樣不謀而合。
- **自我共變異函數 Autocovariance function**
為求計算便利,在此同樣假設 $\beta_0 = 0$。
對於一個 ARMA(1,1) 模型,若 $\beta_0 = 0$,則有以下形式:
$$Y_t = \beta_1 Y_{t-1} + e_t +\theta_1 e_{t-1}$$
我們對等號兩側乘上 $Y_{t-l}$ 藉此計算不同時間點間的交叉動差:
$$Y_t Y_{t-l}- \beta_1 Y_{t-1}Y_{t-l} = e_tY_{t-l} +\theta_1 e_{t-1}Y_{t-l}$$
若此時 $l=1$,並對該等式取期望值:
$$\begin{align}
E[Y_t Y_{t-1}]- \beta_1 E[Y_{t-1}Y_{t-1}] &= E[e_tY_{t-1}] +\theta_1E[ e_{t-1}Y_{t-1} ] \\
\Rightarrow \gamma(1)-\beta_1 \gamma(0) &= 0 + \theta_1 \sigma^2 = \theta_1 \sigma^2
\end{align}$$
又 $\gamma(0) = Var(Y_t) = \frac{(1+\theta_1^2 + 2\beta_1 \theta_1 ) \sigma^2 }{1-\beta_1^2}$,因此
$$\gamma(1) = \sigma^2 \frac{(\beta_1+\theta_1)(1+\beta_1\theta_1)}{1-\beta_1^2}$$
對於 $l \geq 2$,透過相似的計算,可得下列關係式:
$$\gamma(l)-\beta_1 \gamma(l-1)=0$$
如此便可以計算出各階的 ACVF 為:
$$\gamma(l) = \beta_1^{l-1} \gamma(1)$$
- **自我相關函數 Autocorrelation function**
$$\rho(1) = \frac{\gamma(1)}{\gamma(0)} = \frac{\sigma^2 \frac{(\beta_1+\theta_1)(1+\beta_1\theta_1)}{1-\beta_1^2}}{\frac{(1+\theta_1^2 + 2\beta_1 \theta_1 ) \sigma^2 }{1-\beta_1^2}} = \frac{(\beta_1+\theta_1)(1+\beta_1\theta_1)}{1+\theta_1^2 + 2\beta_1 \theta_1}$$
又 $\rho(k) = \frac{\gamma(k)}{\gamma(0)}$,故同樣對於階數 $l \geq 2$,透過相似的計算,可得下列 ACF 關係式:
$$\rho(l) = \beta_1^{l-1} \rho(1)$$
## 6.2.4 ARMA(p,q) 的圖形與模擬
一個定態 ARMA(p,q) 模型結合了 AR\(p) 以及 MA(q) 的特點,這也導致 ARMA 模型在 ACF 與 PACF 的判讀上會有一點困難,並無法一眼就看出其為何階次的 ARMA 模型,以下將分享幾個例子,並且使用 `R` 語言進行模擬。(均設定 $e_t \sim WN(0,1)$)
**1. ARMA(1,1)**
$$Y_t =0.3Y_{t-1} + e_t + 0.7 e_{t-1}$$
```
Input:
library(simts) #使用 simts 套件進行模擬
set.seed(7533967)
#生成資料點 n=500
Y1 <- gen_gts(n = 500,
ARMA(ar = 0.3, ma = 0.7,
sigma2 = 1))
plot(Y1, main = "ARMA(1,1)" ) #繪圖
abline(h=0,lty=2)
```
```
Output:
```

此 ARMA 模型有著均值回歸的現象。
接著,讓我們透過`simts` 內的 `corr_analysis()` 函數來討論 ACF 與 PACF,我們可以透過此函數迅速畫出資料的(偏)自我相關函數。
```
Input:
corr_analysis(Y1)
```
```
Output:
```
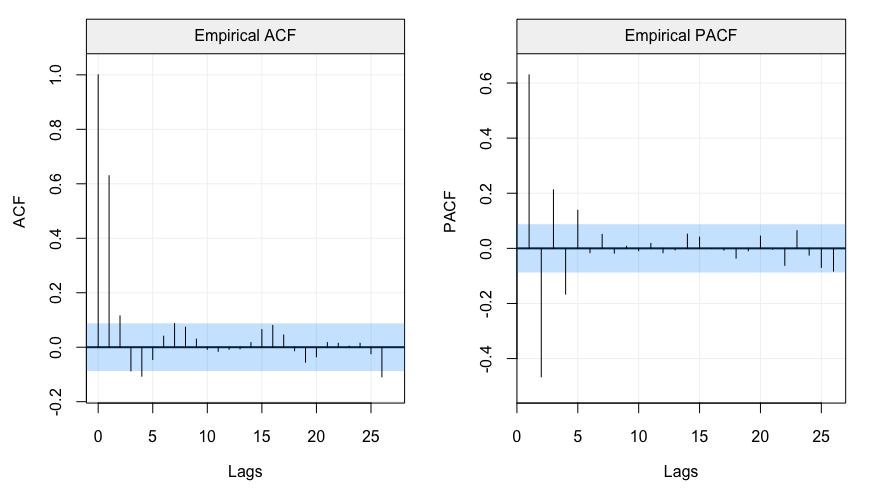
我們可以發現 ARMA(1,1) 的 ACF 與 PACF 都有震盪遞減的現象,這是因為其融合了 AR 以及 MA 模型的特徵,導致我們無法透過圖形輕易地分辨階次。
**2. ARMA(2,2)**
$$Y_t = 1.2 Y_{t-1} - 0.25 Y_{t-2}+ e_t - 0.1 e_{t-1} - 0.75 e_{t-2} $$
```
Input:
library(simts) #使用 simts 套件進行模擬
set.seed(87)
#生成資料點 n=500
Y2 <- gen_gts(n = 500,
ARMA(ar = c(1.2, -0.25),
ma = c(-0.1, -0.75), sigma2 = 1))
plot(Y2, main = "ARMA(2,2)" ) #繪圖
abline(h=0,lty=2)
```
```
Output:
```

我們可以看到,由於 MA 的階次提高,先前所遭受之隨機衝擊會殘留較長時間,均值回歸的速度會看起來較慢。
我們一樣來畫出 ACF 與 PACF:
```
Input:
corr_analysis(Y2)
```
```
Output:
```

透過 ACF、PACF 圖形,我們可以稍微判斷該時間序列比較像哪一種模型較為合適,但如同在 ARMA 模型中所看到的,圖形並無法清楚地讓研究者得知確切的階數為何。
## 6.2.4 為 ARMA(p,q) 定階
我們在討論模型設定時,並不會希望模型過於複雜,因此原則上會希望 **p+q 越小越好**,那麼如何找到合適的 p、q 的階數呢?
1. **判別 ACF、PACF 圖形**
從先前幾個章節中,我們認識到 AR、MA 以及 ARMA 模型之 ACF 和 PACF 的性質,當我們拿到一個時間序列資料,不妨將其的 ACF、PACF 繪製出來做為參考。
(參考文章及 `R` 程式碼:[R语言时序-AR、MA与ARMA的判断及定阶](https://blog.csdn.net/weixin_39982225/article/details/120623005))
在下方圖表中,tails off 指 ACF 或 PACF 會呈現遞減下滑,而 cut off 指 ACF 或 PACF 在過了某個點後即歸零。總的來說,使用圖形方法是個研究的起點,但光用肉眼來判斷是不夠準確,但至少能幫助我們縮小研究討論的範圍。
<img style="display: block; margin: auto;"
src="https://d3i71xaburhd42.cloudfront.net/c34658240bd2d05020cf61e7f26c8fd5db73d82a/3-Table1-1.png" width="60%">
<p style="text-align: center;">
各模型 ACF、與 PACF 性質。<br>
來源:<a href="https://www.semanticscholar.org/paper/Forecasting-Of-Time-Series-Data-Using-Hybrid-ARIMA-Valvi-Shah/c34658240bd2d05020cf61e7f26c8fd5db73d82a">Valvi, J.R., & Shah, P.K. (2018)</a>
</p>
2. **使用訊息量準則 (Information criterion)**
在進行統計模型的設定時,變數的個數究竟要放多少一直是個重要的議題,我們希望模型能夠精簡且準確,而提升準確性到一個方法就是加入更多的變數,這會導致模型的變異升高,這就是我們所謂的**偏差與方差之權衡 (Bias-Variance Tradeoff)**,而在時間序列的迴歸模型中就是要探討落後期數的問題。
(詳見:[Anand Avati(2019), Bias-Variance Analysis: Theory and Practice](https://cs229.stanford.edu/summer2019/BiasVarianceAnalysis.pdf))
而為了解決此問題,其中一個方法即為使用**訊息量準則 (Information criterion)**,訊息量準則基本上是在關注模型適配度的同時,對於模型複雜度進行懲罰,常見的訊息量準則模式可以寫成:$\text{IC}=-2\ln L(\hat{\theta})+c(\cdot)$,其中第一項衡量模型配適度,第二項則是對模型的複雜度進行懲罰,我們希望可以在兩者中找到平衡,也就是找到使得訊息量準則之值最小的模型,在統計學領域中最常見的訊息量準則有 **AIC (赤池訊息量準則)** 和 **BIC (貝氏訊息量準則)** 兩者。
<img style="display: block; margin: auto;"
src="https://upload.wikimedia.org/wikipedia/commons/thumb/9/9f/Bias_and_variance_contributing_to_total_error.svg/461px-Bias_and_variance_contributing_to_total_error.svg.png" width="80%">
<p style="text-align: center;">
偏差與方差之權衡 Bias-Variance Tradeoff。<br>
來源:<a href="https://en.wikipedia.org/wiki/Bias%E2%80%93variance_tradeoff">Wikipedia</a>
</p>
- **Akaike Information Criterion 赤池訊息量準則 (AIC)**
一般而言,AIC 會有以下形式的表示:
$$\text{AIC} = -2\ln L(\hat{\theta}) +2k$$
第一項 $-2\ln L(\hat{\theta})$ 透過最大概似法計算出的 likelihood 來衡量模型的配適度,而第二項的 $2k$ 則是對模型複雜度的懲罰項,$k$ 為模型中變數的數量,因此在 ARMA 的模型中 $k=p+q$,而我們會希望 AIC 的數值**越小越好**。
然而,在樣本數較少的情況下,AIC 可能會建議一個較為複雜的模型,而為了處理此問題,發展出了 **AICc (Corrected Akaike Information Criterion)**,即 AIC 的修正版本,將待估計參數數量與樣本數 $n$ (或觀察期數 $T$) 進行連結,公式如下:
$$\text{AICc} = \text{AIC} + \frac{2k(k+1)}{T-k-1}$$
- **Bayesian Information Criterion 貝氏訊息量準則 (BIC)**
讓我們接著討論 BIC,BIC 通常會有以下形式的表示:
$$\text{AIC} = -2\ln L(\hat{\theta}) + k \ln T$$
BIC 與 AIC 不同的地方在於懲罰項的部分與樣本數 (觀察到的期數) 有關,若 $T >8$,則 $\ln T>2$ ,而同樣地 $k=p+q$,因此 BIC 對於模型複雜度的懲罰效果常會比 AIC 來得大,因而會傾向**挑選到較為精簡 (落後期數較少) 的模型**。
此外,亦有其他訊息量準則或是類似的方法,如 HQC (Hannan-Quinn criterion) 或是 $\text{Mallow's}\ C_p$,可見 [Guerrier et al. (2019)](https://smac-group.github.io/ts/the-family-of-autoregressive-moving-average-models.html#model-selection)。
若想對 AIC、BIC 有更完整的暸解,可以延伸閱讀[顏妤樺 (2019) 《AIC、BIC 和 EBIC 之回顧》](https://thesisapi.lib.nycu.edu.tw/server/api/core/bitstreams/3ad6ba47-ee95-42d2-abf0-0f04c6248b7a/content)及 [Cavanaugh & Neath (2019). The Akaike information criterion: Background, derivation, properties, application, interpretation, and refinements](https://iowabiostat.github.io/research-highlights/joe/Cavanaugh_Neath_2019.pdf),此二文章內有對於 AIC、BIC 的推導以及比較。此外,若對於不同訊息量準則間的實證比較有興趣,可參考[虞國興、劉治均 (1995)《時間序列模式選取準則之比較》](https://www.twaes.org.tw/ae/htmdata/04101015.pdf)。
<img style="display: block; margin: auto;"
src="https://miro.medium.com/v2/resize:fit:1100/format:webp/1*KaeyCUsse4iL6zRnOKtSMQ.png" width="100%">
<p style="text-align: center;">
ARMA(p,q) 定階方法的比較。<br>
來源:<a href="https://medium.com/r-%E8%AA%9E%E8%A8%80%E8%87%AA%E5%AD%B8%E7%B3%BB%E5%88%97/r%E8%AA%9E%E8%A8%80%E8%87%AA%E5%AD%B8%E6%97%A5%E8%A8%98-14-arima%E6%A8%A1%E5%9E%8B%E7%B0%A1%E4%BB%8B%E8%88%87%E5%AE%9A%E9%9A%8E-d1fa7037c53d">Edward Tung,ARIMA模型簡介與定階</a>
</p>
在 `R` 中,我們可以簡單地透過 `AIC()`、`BIC()` 函數去計算該模型的訊息量準則。
```
Input:
# 生成 ARMA(2,2) 的模擬資料
set.seed(123)
arma_data <- arima.sim(model = list(ar = c(0.5, -0.2), ma = c(0.4, -0.3)), n = 500)
# 建立一個空的表格,存放每個模型的 AIC 和 BIC
results <- data.frame(Order = character(),
AIC = numeric(),
BIC = numeric())
# 使用迴圈計算 ARMA(1,1) 到 ARMA(3,3) 模型,並存放 AIC 和 BIC
for (p in 1:3) {
for (q in 1:3) {
model <- arima(arma_data, order = c(p, 0, q))
results <- rbind(results, data.frame(Order = paste("ARMA(", p, ",", q, ")", sep = ""),
AIC = AIC(model),
BIC = BIC(model)))
}
}
#輸出結果
print(results)
```
```
Output:
Order AIC BIC
1 ARMA(1,1) 1411.953 1428.812
2 ARMA(1,2) 1403.259 1424.332
3 ARMA(1,3) 1398.682 1423.970
4 ARMA(2,1) 1403.704 1424.777
5 ARMA(2,2) 1398.266 1423.554
6 ARMA(2,3) 1400.250 1429.752
7 ARMA(3,1) 1401.539 1426.827
8 ARMA(3,2) 1400.253 1429.755
9 ARMA(3,3) 1402.195 1435.912
```
結果顯示,ARMA(2,2) 為最佳模型。
3. **Extended auto-correlation function (EACF)**
由於 ARMA 模型的 ACF 與 PACF 數值皆為無限地隨著階數逐步下降,並無一個明確的斷點可供參考,因此 [Tsay & Tiao (1984)](https://www.tandfonline.com/doi/abs/10.1080/01621459.1984.10477068) 提出新的研究方法,也就是擴展的樣本自我相關函數 (Extended Sample Autocorrelation Function),我們在此簡稱其為 EACF,EACF 是一種透過檢定的方式討論樣本的時間序列是否為某特定的 ARMA(p,q) 過程。
我們已知若 $Y_t$ 是一個 ARMA(p,q) 模型,在**不考慮常數項**的話,可以寫成:
$$\beta(L)Y_t = \theta(L)e_t$$
其中:
$$\begin{align}
\beta(L) &= 1-\beta_1L -\beta_2L^2-\cdots-\beta_pL^p \\
\theta(L) &= 1+ \theta_1L + \theta_2L^2 +\cdots+ \theta_qL^q
\end{align}$$
等號的左側為 AR 部分,而等號右側則代表 MA 部分。
若我們把模型中的 AR 或 MA 過程令為 $Z_t$,寫作:
$$\begin{align}
Z_t &= \beta(L)Y_t \\
&= (1-\beta_1L -\beta_2L^2-\cdots-\beta_pL^p)Y_t\\
&= \theta(L)e_t\\
&=(1+ \theta_1L + \theta_2L^2 +\cdots+ \theta_qL^q)e_t
\end{align}
$$
而這種將 ARMA(p,q) 模型分開來探討的概念,就是本章節的核心。
我們假設現在有一個資料 $Y_t$ 是來自一個 ARMA(p,q) 模型,若我們用 AR($p$) 去配適資料,則我們會得的一串不一致的估計如下:
$$Y_t = \sum^{p}_{i=1} \hat{\beta}_i^{(0)} Y_{t-i} + \hat{e_t}^{(0)} $$
等號重新平衡可得:$\hat{e_t}^{(0)} = Y_t - \sum^{p}_{i=1} \hat{\beta}_i^{(0)} Y_{t-i}$
那這樣錯誤的殘差估計就不會是我們期望的白噪音,又如果今天 $q\geq 1$,當然就表示殘差中包含形成 $Y_t$ 的部分資訊,讓我們接下來對這些迴歸式進行迭代,我們從加入前一期的殘差項估計 $\hat{e}_{t-1}^{(0)}$ 開始,新的迴歸式是這樣子的:
$$Y_t = \sum_{i=1}^p \beta_i^{(1)}Y_{t-i}+\theta_1^{(1)}\hat{e}_{t-1}^{(0)} + e_t^{(1)}$$
在這兩條迴歸式中,右上角的括弧代表第幾次迭代所得的對應的誤差項。
在第 (1) 次的迭代中,如果 ARMA(p,q) 的 $q=1$,則 OLS 所估計出的 $\hat{\beta}_i^{(1)}$ 會是具備一致性 (consistency);同理,若 $q>1$,則此估計則會變得不具一致性,而殘差 $\hat{e}_{t}^{(1)}$ 也不會是白噪音過程。
讓我們再來進行一次迭代,不止加入前一期的殘差估計,也再放入往前二期的殘差估計,詳細迴歸式如下:
$$Y_t = \sum_{i=1}^p \beta_i^{(2)}Y_{t-i}+\theta_1^{(2)}\hat{e}_{t-1}^{(1)}+ \theta_2^{(2)}\hat{e}_{t-2}^{(0)} + e_t^{(2)}$$
同樣地,如果 $q=2$,則上式的係數估計會具備一致性,則 $q>2$ 就不具備一致性。經由這兩期迭代的展現,我們可以去寫出用 AR($p$) 搭配不同的 MA(q) 來去配適模型的一般式,以迭代 q 次為例:
$$Y_t= \sum_{i=1}^p \beta^{(q)}_i Y_{t-i} + \sum_{i=1}^q \theta_{i}^{(q)}\hat{e}_{t-i}^{(q-i)} +e_t^{(q)}$$
因此,我們得到的迭代 q 次殘差估計為:
$$\hat{e}_t^{(q)} = Y_t - \sum_{i=1}^p \hat{\beta}^{(q)}_i Y_{t-i} - \sum_{i=1}^q \hat{\theta}_{i}^{(q)}\hat{e}_{t-i}^{(q-i)}$$
如果資料的 DGP 是來自於 ARMA(p,q),但我們不知道真實的 p 和 q 為多少,[Tsay & Tiao (1984)](https://www.tandfonline.com/doi/abs/10.1080/01621459.1984.10477068) 透過迭代的方式計算 EACF 讓我們能去估計階次 p 和 q。EACF 的想法大至上是這樣的,若我們先鎖定先鎖定的階次 $m=0,1,2,\cdots$,我們就可以針對 AR($m$) 為起點,並且進行 $j$ 次迭代,便可找出去對應的係數 $\hat{\beta}_i^{(j)}$ $\text{(} i=1,\cdots,m \text{)}$。
我們定義 $Z_{t}^{(j)} = (1-\hat{\beta}^{(j)}_1L -\cdots-\hat{\beta}^{(j)}_mL^m)Y_t$,並且將此式的 ACF 稱為落後 $j$ 期的第 $m$ 個 **EACF**,記為$\hat{\rho}_j^{(m)}$。透過展開 $j$ 與 $m$,我們可以得到下方的 EACF表格。
<img style="display: block; margin: auto;"
src="https://hackmd.io/_uploads/HyNzAbtKJx.png" width="100%">
<p style="text-align: center;">
EACF 與 ARMA(p,q) 的對照表。<br>
來源:<a href="https://www.amazon.com/Time-Analysis-Univariate-Multivariate-Methods/dp/0321322169">William W. S. Wei (2006)</a>
</p>
而對於 $\hat{\rho}_j^{(m)}$ 我們有以下的大樣本性質:
$$\hat{\rho}_j^{(m)}\stackrel{p}{\rightarrow}
\begin{cases}
0 & ,0 \leq m-p <j-q \\
\text{X} \neq 0 & ,\text{ o.w.}
\end{cases}
$$
這個大樣本性質對應到了 MA(q) 的 ACF 的斷點 (cuts off)性質。
當然,我們在計算實際的 EACF 時,不可能會算出剛好為 0 的數值,此時我們就需要針對白噪音的分配進行檢定,通常我們會採取兩倍標準差的信賴區間。
$$
\begin{cases}
\text{If} \ |\hat{\rho}_j^{(m)}| < \frac{2}{\sqrt{T}} \rightarrow \text{O} \\
\text{If} \ |\hat{\rho}_j^{(m)}| \geq \frac{2}{\sqrt{T}} \rightarrow \text{X}
\end{cases}
$$
我們接著便可透過此分類準則將 EACF 表格轉換為視覺上較為清楚的檢定後表格,我們會針對 $\text{O}$ 所構成之三角形之頂點作為我們所辨認出來的 ARMA(p,q) 之階數。
<img style="display: block; margin: auto;"
src="https://hackmd.io/_uploads/SJeAvibF1l.png" width="100%">
<p style="text-align: center;">
ARMA(1,1) 理論上的 EACF 表格。<br>
來源:<a href="https://link.springer.com/book/10.1007/978-0-387-75959-3">Cryer and Kung-Sik Chan (2008)</a>
</p>
雖然 EACF 是一種相對複雜的檢定方法,但在實際應用上可透過 `TSA` 套件中的 `eacf()` 函數進行表格的計算。
```
Input:
# 生成 ARMA(1,1) 的模擬資料
library(simts)
Y1 <- gen_gts(n = 500,
ARMA(ar = 0.3, ma = 0.7,
sigma2 = 1))
# 載入 TSA 套件
library(TSA)
# 計算 EACF
eacf(Y1)
```
```
Output:
AR/MA
0 1 2 3 4 5 6 7 8 9 10 11 12 13
0 x x o o o o o o o o o o o o
1 x o o o o o o o o o o o o o
2 x x o x o o o o o o o o o o
3 x x x o o o o o o o o o o o
4 x x x x o o o o o o o o o o
5 x x x x x o x o o o o o o o
6 x x x x x x x o o o o o o o
7 x x x x x x x o o o o o o o
```
左上方的頂點為 ARMA(0,2) 與 ARMA(1,1),我們便可以從此二候選模型開始做模型的設定與研究。
# 6.3 ARIMA 模型
我們先前在 [Ch5](https://hackmd.io/@wwwh0225/ryhv0fVL0#52-p-%E9%9A%8E%E8%87%AA%E6%88%91%E8%BF%B4%E6%AD%B8%E6%A8%A1%E5%9E%8B-ARp) 有介紹過隨機漫步模型 (random walk model),可以用以下形式表示:$Y_t = Y_{t-1} + e_t,\ e_t \overset{\mathrm{i.i.d.}}{\sim} (0,\sigma^2)$,而我們知道此並非一個定態的時間序列。在我們實際的資料中,常常也會存在非定態時間序列的情形,透過一些技巧,我們能將非定態時間序列轉為定態的時間序列後再進行分析。
## 6.3.1 固定趨勢模型
在觀察某些時間序列資料時,數據可能看起來有著某種跟時間經過有關的固定趨勢,如下方圖片中的 GDP 資料,看起來每年都服從一個固定的成長幅度,我們便可以嘗試使用固定趨勢模型去進行配適。
<img style="display: block; margin: auto;"
src="https://today-obs.line-scdn.net/0hgK9LowYdOGQENRC9R5FHMz1jOws3WStnYANpZ0dbZlB9Vis3bAR1USgzNQR9A386alt-ByVwZwd-VXk2bFE/w1200" width="75%">
<p style="text-align: center;">
我國各年度 GDP 表現<br>
來源:<a href="https://today.line.me/tw/v2/article/6nZLMj">股感知識庫Stockfeel <GDP,衡量國家經濟成長的常見指標
></a>
</p>
對於一個固定趨勢模型 $\{Y_t\}$,我們可以對其有以下的簡單設定:
$$Y_t = \beta_0 + \beta_1t + e_t,\ e_t \overset{\mathrm{i.i.d.}}{\sim} (0,\sigma^2)$$
因此,其動差條件為:
$$\begin{align}
E[Y_t] &=\beta_0 + \beta_1t \\
Var[Y_t] &=\sigma^2
\end{align}$$
我們對其是否為定態感到興趣,我們計算當時間為 $t=t+s$ 時,$\{Y_t\}$ 的動差為何:
$$\begin{align}
E[Y_{t+s}] &=\beta_0 + \beta_1{(t+s)}\\
&=\beta_0 + \beta_1t + \beta_1s\\
&=E[Y_t] + \beta_1s \\
& \neq E[Y_t]
\end{align}$$
因此,$\{Y_t\}$ 不是一個定態的時間序列。
而要處理這種非定態的時間模型,一個常見的做法是將資料進行「**差分**」,透過此法將資料轉換為定態的時間序列,如此便可以進行後續的研究分析。
$Y_t$ 的一階差分為:
$$\begin{align}
\Delta Y_t &= Y_t - Y_{t-1} \\
&= (\beta_0 + \beta_1t + e_t) -(\beta_0 + \beta_1(t-1) + e_{t-1}) \\
&= \beta_1 +e_t - e_{t-1}
\end{align}$$
我們可以將其視為**有限階次**的 MA 模型,因此 $\Delta Y_t$ 為**定態**的時間序列。
:::info
💡 固定趨勢不一定只有線性模式,也可能存在二次或更高階次之多項式,如:$Y_t = \beta_0 + \beta_1t + \beta_2t^2 + e_t$。
:::
但對固定趨勢進行差分所獲得的 $\Delta Y_t$ 為一**不可逆**的 MA 模型,也就是說其無法轉換為對偶的 AR 模型,這會使我們的模型的預測性或說穩定性下降,而過去所受到的隨機衝擊也可能不會隨著時間流逝而減低。
如果知道時間序列有固定趨勢,一個比較好的做法是對固定趨勢進行估計後再將其移除,得到去趨勢後的定態時間序列,稱**去趨勢後定態 (trend stationary, TS)**。
接續先前的範例 $Y_t = \beta_0 + \beta_1t + e_t,\ e_t \overset{\mathrm{i.i.d.}}{\sim} (0,\sigma^2)$,我們可以對其進行估計,得到以下的迴歸模型:
$$Y_t = \hat{\beta_0} + \hat{\beta_1}t + \hat{e_t}$$
而後將資料進行配適,得到 $\hat{Y_t}=\hat{\beta_0} + \hat{\beta_1}t$ 作為固定趨勢的估計,接著便可以得到定態的殘差序列 $\hat{e_t}$:
$$\hat{e_t} =Y_t-\hat{Y_t} = Y_t - \hat{\beta_0} + \hat{\beta_1}t $$
## 6.3.2 隨機趨勢模型
在 [Ch5](https://hackmd.io/@wwwh0225/ryhv0fVL0#ch5) 中,我們曾提到 具有單根的 AR(1) 是具有飄移項之隨機漫步模型,也就是其具有所謂「隨機趨勢」,即時間序列資料有著長期的隨機變化,
若一個 ARMA(p,q) 模型具有隨機趨勢,或著是說其具有「單根」,則此時間序列並非定態。說明如下所示:
我們考慮以下 **ARMA(p,q)** 模型:$\beta(L)Y_t=\theta(L)e_t,\ e_t \overset{\mathrm{i.i.d.}}{\sim} (0,\sigma^2)$。
如果方程式 $\beta(z)=0$ 存在單根,也就是有一個根為 1,而我們可以改寫 $\beta(z)$ 為:$\beta(z)=(1-z)\tilde{\beta}(z)$。若 $\tilde{\beta}(z)=0$ 的根都在單位圓之外,則原本的模型可以改寫為:
$$\begin{align}
& (1-L)\tilde{\beta}(L)Y_t=\theta(L)e_t\\
\rightarrow & (1-L)Y_t=\tilde{\beta}(L)^{-1}\theta(L)e_t
\end{align}$$
而我們可以接著定義$u_t=\tilde{\beta}(L)^{-1}\theta(L)e_t$ 為一個定態時間序列,因此可改寫成 $(1-L)Y_t=u_t$。
最後,我們便可將 $Y_t$ 改寫成下列等式:
$$Y_t = Y_{t-1} + u_t = Y_0 + \sum_{s=1}^t u_s$$
而這就回到隨機漫步的形式,而 $\sum_{s=1}^t u_s$ 的這個部分和 (partial sum) 就稱為「**隨機趨勢**」 (stochastic trend)。
關於隨機趨勢對迴歸分析所造成的問題,可參見此[**連結**](https://bookdown.org/machar1991/ITER/14-7-nit.html)。
## 6.3.3 差分後定態
對於存有隨機趨勢的序列,如隨機漫步過程:$Y_t = Y_{t-1} + e_t,\ e_t \overset{\mathrm{i.i.d.}}{\sim} (0,\sigma^2)$,若我們對其進行一階差分,可得:
$$\begin{align}
\Delta Y_t &= Y_t - Y_{t-1} \\
&= (Y_{t-1} + e_t) - Y_{t-1} \\
&=e_t
\end{align}$$
因此,$\Delta Y_t$ 為一個定態的時間序列,我們稱其為**差分後定態 (difference stationary, DS)**。
:::info
💡 若 $\{Y_t\}$ 為定態時間序列,且其長期變異數有限且大於零,則我們稱 $\{Y_t\}$ 為 $I(0)$ 序列,可表示為 $Y_t \sim I(0)$。
而 $I(1)$ 則為經過經過一階差分後成為的時間序列,稱為**一階自積 (integrated of order one)**。比如若 $\{Y_t\}$ 服從一個簡單隨機過程,經過一階差分後就會變成定態,則可表示 $Y_t \sim I(1)$。
以此類推,若序列 $\{Y_t\}$ 得經過 d 階差分才會成為 $I(0)$,則表示為 $Y_t \sim I(d)$。
而在此處所用到的符號 $I$,就是 $\text{ARIMA}$ 模型中間的那個 $\text{I}$。
:::
## 6.3.4 ARIMA 模型
**ARIMA** (Autoregressive Integrated Moving Average) 模型可以表示為 $ARIMA(p,d,q)$,其實就是 ARMA 模型的拓展,指的就是時間序列 $\{Y_t\}$ **經過 d 階差分後為一個 ARMA(p,q) 過程**。
$\{Y_t\}$ 的 d 階差分可以記為 $\Delta^d Y_t = (1-L)^d Y_{t}$,而在實務上多是探討 $d \leq 2$ 的情況。綜上所述,$ARIMA(p,d,q)$ 可以表現成以下模式:
$$\beta(L) \color{red}{(1-L)^d Y_t} = \beta_0 + \theta(L)e_t$$
我們接下來用 `R` 模擬 ARIMA 過程:
```
Input:
library(forecast)
# 設定 ARIMA(1,1,1) 模型的參數
# ARIMA 模型參數:AR(1) = 0.5, I = 1, MA(1) = -0.3, 常數 = 10
arima_111 = arima.sim(n = 100,
model = list(order = c(1, 1, 1),
ar = 0.5, ma = -0.3),
mean = 10)
plot(arima_111)
#這會出現一個有趨勢的圖形
```
```
Output:
```
<img style="display: block; margin: auto;"
src="https://ppt.cc/ff4N4x@.png" width="75%">
```
Input:
#進行差分 使用 diff() 函數
plot(diff(arima_model))
#如此便出現定態的序列了!
```
```
Output:
```
<img style="display: block; margin: auto;"
src="https://ppt.cc/fBg8Tx@.png" width="75%">
# 6.4 季節性模型
<img style="display: block; margin: auto;"
src="https://hackmd.io/_uploads/HkxxX53mR.png" width="80%">
<p style="text-align: center;">
呈週期變化的 AirPassengers 資料集<br>
</a>
</p>
## 6.4.1 Classical Decomposition
在時間序列中,我們是在研究變數的自我相關性,而一個時間序列一般而言可以被拆分成三個部分:趨勢、季節因子與隨機誤差項。**Classical Decomposition** 提供我們一個基本的模型架構去萃取時間序列中的這些部分。
**Classical Decomposition** 通常有以下兩種形式:
- 加法模型 Additive decomposition:$Y_t=T_t + S_t+e_t$
- 乘法模型 Multiplicative decomposition:$Y_t=T_t \cdot S_t \cdot e_t$
($T_t$:趨勢、$S_t$:季節性、$e_t$:隨機項)
兩模型的選擇的邏輯如下圖所示:
<img style="display: block; margin: auto;"
src="https://ppt.cc/fDx7Zx@.jpg" width="80%">
拆解的步驟如下:
1. **提取趨勢**
先決定週期數 $m$,如四季為一週期,則 $m=4$;而若以一年中十二個月作為週期,則 $m=12$。
使用 **Centred moving average (CMA)** 方法來衡量趨勢,CMA 的計算與 $m$ 的取值有關:
以下為 $m=3$ 時之 CMA範例:
$$\text{3-MA} = \frac{Y_{t-1} + Y_t + Y_{t+1}}{3}$$
即由 $Y_t$ 為中心共三期的移動平均。
**CMA** 的使用公式是這樣的:$m\text{-MA} = \frac{1}{m} \sum_{i=\frac{-(m-1)}{2}}^{\frac{(m-1)}{2}}Y_{t+i}$
但這個取值在 $m$ **為偶數**時,就會**喪失其對稱性**,因此需要新的解決方法。
舉例來說,若 $m=4$ 則需要再多滑動一下,然後再取平均:
$$\begin{align}
2\times \text{4-MA} &= \frac{1}{2}(\frac{Y_{t-2}+Y_{t-1}+Y_{t}+Y_{t+1}}{4}) + \frac{1}{2}(\frac{Y_{t-1}+Y_{t}+Y_{t+1}+Y_{t+2}}{4})\\
&= \frac{1}{8}Y_{t-2}+ \frac{1}{4}Y_{t-1}+\frac{1}{4}Y_{t}+\frac{1}{4}Y_{t+1}+\frac{1}{8}Y_{t+2}
\end{align}$$
$2\times \text{m-MA}$ 的公式如下:
$$2\times \text{m-MA} = \frac{1}{m}\left(\frac{1}{2}\left(Y_{t+(m-1)/2}+Y_{t-(m-1)/2}\right) + \sum_{i=-(m-2)/2}^{(m-2)/2} Y_{t+i}\right)$$
根據 $m$ 為奇數或偶數,我們套用不同對應的 CMA 公式來計算 $T_t$。
2. **去除趨勢**
若我們估計出之趨勢項為 $\hat{T_t}$ 後,便可以進行趨勢去除 (de-trend),我們令去除趨勢後之時間序列為 $\{\tilde{Y_t}\}$。
- 加法模型 Additive decomposition:$\tilde{Y_t}=Y_t-\hat{T_t} = \hat{S_t}+\hat{e_t}$
- 乘法模型 Multiplicative decomposition:$\tilde{Y_t}=\frac{Y_t}{\hat{T_t}}= \hat{S_t} \cdot \hat{e_t}$
3. **計算季節因子**
根據對應之季節性資料計算每個季節去除趨勢後的均數,以此作為季節性因子。舉例來說,若我們搜集累積五年的月資料,並且依序以 $Y_1$、$Y_2$ ... 紀錄,則一月份的季節因子為:
$$S_{Jan} = \frac{\tilde{Y_1}+\tilde{Y_{13}}+\tilde{Y_{25}}+\tilde{Y_{37}}+\tilde{Y_{49}}}{5}$$
$S_{Jan}$ 之值便可以帶入每一筆一月份的資料 (t=1,13,25,...) 作為季節因子的估計。
4. 計算隨機項
- 加法模型 Additive decomposition:$\hat{e_t}=\tilde{Y_t} - \hat{S_t}$
- 乘法模型 Multiplicative decomposition:$\hat{e_t} = \frac{\tilde{Y_t}}{\hat{S_t}}$
- 若模型無季節性,則 $\hat{e_t} = \tilde{Y_t}$
## 6.4.2 用程式去除季節性因子
我們同樣以著名的 `AirPassengers` 資料集為例,使用內建函數
首先載入資料,並將其轉換成時間序列格式:
```
Input:
air_data <- ts(AirPassengers,frequency = 12)
decomposed <- decompose(air_data, type = "additive") #乘法模型可選 "multiplicative"
print(decomposed)
```
`print(decomposed)` 就可以輸出所有拆解後的變量。
我們可用圖片來看出序列中的各個部分:
```
Input:
plot(decomposed)
```
```
Output:
```
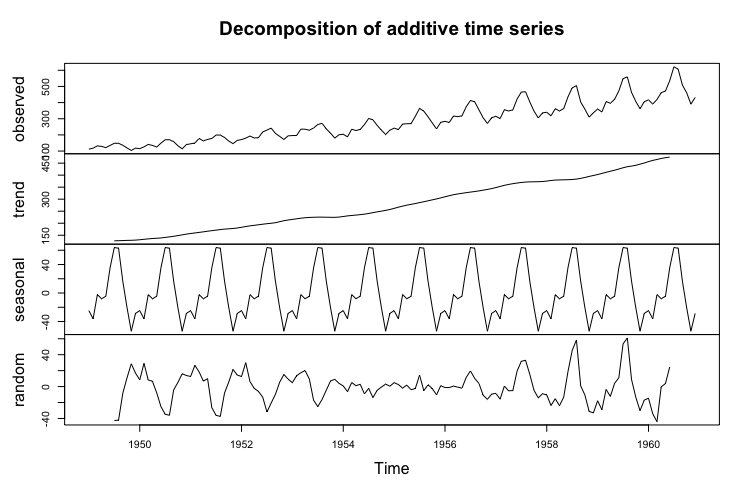
而透過疊圖分析,我們可以看出時間序列有無去除季節性因子的區別:
```
Input:
# 提取去除季節性後的數據
deseasonalized_data <- air_data - decomposed$seasonal
# 設置繪圖區域為兩個子圖
par(mfrow = c(1, 1),
family = "Heiti TC") # 這個設置將繪圖設為單一圖像 # 設定中文字體
# 繪製原始數據的線圖
plot(air_data, col = "blue", lwd = 2,
main = "AirPassengers: 原始與去季節性數據",
ylab = "Passengers",
xlab = "Year",
family = "Heiti TC") # 設定中文字體
# 在同一個圖上繪製去除季節性後的數據
lines(deseasonalized_data, col = "red", lwd = 2)
# 添加圖例
legend("topright",
legend = c("原始數據", "去季節性後的數據"),
col = c("blue", "red"),
lwd = 2)
```
```
Output:
```
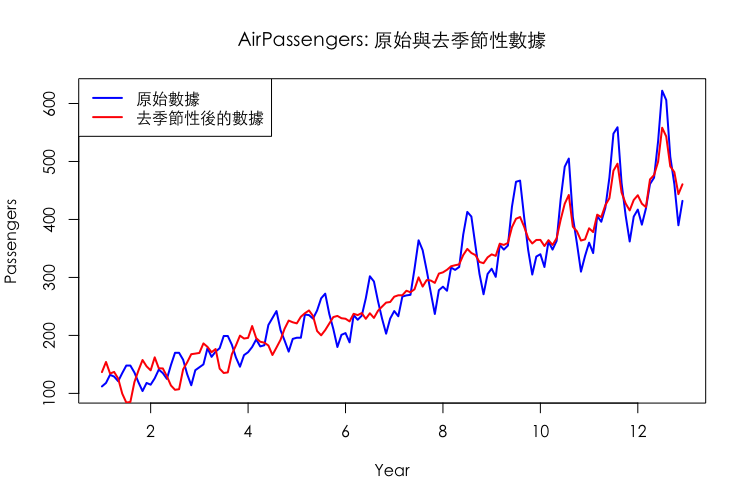
## 6.4.3 季節性(Seasonal) ARIMA
在先前所研究的 ARMA 模型中,我們探討時間序列中跨期間的關係,但在實務上,其實時間序列跨期的資料常常伴隨著「季節週期性」,比方說百貨公司的銷售資料可能就會和每年度 10 月所舉辦的週年慶活動有顯著影響,在進行跨年度比較時,可能需要進行另外的處理,我們便可以將 ARMA 拓展成 SARIMA,此處的 S 正式我們討論的季節性因素。
SARIMA 通常會以下列形式作表示:
$$\text{ARIMA}\underbrace{(p,d,q)}_{\text{non-seasonal part}}\times\underbrace{(P,D,Q)}_{\text{seasonal part}}S $$
各項符號如下表所示,分為季節部分以及非季節部分:
| 參數 | 解釋 |
|------|------------------------|
| p | 非季節性自我迴歸階數 |
| q | 非季節性移動平均階數 |
| d | 一階差分次數 |
| P | 季節性自我迴歸階數 |
| Q | 季節性移動平均階數 |
| D | 季節性差分次數 |
| S | 季節/週期循環長度 |
首先,我們可先看到週期循環長度的參數 $S$,$S$ 根據資料型態會有所不同,可能為若以一年的時間跨度來說,$S=4$ 可能為季資料的週期,$S=12$ 可能為月資料的週期;而 $(P,D,Q)$ 則為對應週期 $S$ 所延伸出的跨期自我迴歸與移動平均,透過落後運算元 $L^S$ 便可以拓展 ARMA 模型,使之進一步地考慮到季節的週期性。
以下是一個均數為 0 的 SARIMA 過程:
$$\Phi(L^S)\phi(L)Y_t=\Theta(L^S)\theta(L)e_t$$
其中非季節性的 lag-polynomial:
$$\begin{align}
\phi(L) &= 1-\phi_1L -\phi_2L^2-\cdots-\phi_pL^p \\
\theta(L) &= 1+ \theta_1L + \theta_2L^2 + \cdots + \theta_qL^q
\end{align}$$
而季節性的 lag-polynomial:
$$\begin{align}
\Phi(L) &= 1-\Phi_1L -\Phi_2L^{2S}-\cdots-\Phi_pL^{PS} \\
\Theta(L) &= 1+ \Theta_1L + \Theta_2L^{2S} + \cdots + \Theta_qL^{QS}
\end{align}$$
簡單來說,SARIMA 就可以看作是在 ARIMA 的基礎上疊加季節性變量。而辨別 SARIMA 的方法,除了透過經驗法則統整週期之外,我們也可以透過 ACF/PACF 圖去看 ACF/PACF 脫離信賴區間的狀態是否有週期性,藉此進行定階。由於篇幅的關係,關於 SARIMA 的進一步解釋與實作,可參閱 [Milla(2024)](https://rpubs.com/bertmilla/1174180),其餘內容於本文就不再贅述。
# 參考資料
1. 陳旭昇(2022)。《時間序列分析: 總體經濟與財務金融之應用》(3版)。
2. 陳旭昇(2015)。《統計學: 應用與進階》(3版)。
3. 楊奕農(2017)。《時間序列分析: 經濟與財務上之應用》(3版)。
4. 葉小蓁(1998)。《時間序列分析與應用》。
5. [顏國勇(2011)。《機率論》,電子書。](https://library.math.ncku.edu.tw/documents/1/Probability21A.pdf)
6. [北京大學「金融時間序列分析」講義](https://www.math.pku.edu.cn/teachers/lidf/course/fts/ftsnotes/html/_ftsnotes/ftsnotes.pdf)。
7. [北京大學「金融中的随机数学」講義](https://www.math.pku.edu.cn/teachers/lidf/course/stochproc/stochprocnotes/html/_book/index.html)。
8. [南京大學「时间序列分析」講義](https://www.lamda.nju.edu.cn/yehj/timeseries2021/)。
9. Klaus Neusser (2015), Time Series Analysis in Economics, Springer.
10. Fumio Hayashi (2000), Econometrics, Princeton University Press.
11. Jonathan D. Cryer and Kung-Sik Chan (2008), Time Series Analysis with Applications in R, Springer.
12. Paul S.P. Cowpertwait and Andrew V. Metcalfe (2009), Introductory Time Series with R, Springer.
13. Walter Enders (2015), Applied Econometric Time Series, Wiley.
14. [Christoph Hanck, Martin Arnold, Alexander Gerber, and Martin Schmelzer(2024), Introduction to Econometrics with R.](https://www.econometrics-with-r.org/index.html)
15. Bruce E. Hansen (2021), Econometrics, Princeton University Press.
16. Steven Shreve (2003), Stochastic Calculus for Finance”, Vol 2, Springer.
17. [Rao, S. S. (2008). A course in time series analysis. In Technical Report. Texas A&M University.](https://web.stat.tamu.edu/~suhasini/teaching673/time_series.pdf)
18. [Guerrier et al. (2019), Applied Time Series Analysis with R.](https://smac-group.github.io/ts)
19. Ruey Tsay (2010), Analysis of Financial Time Series.
20. William W. S. Wei (2006), Time Series Analysis : Univariate and Multivariate Methods
21. ByoungSeon Choi (1992), ARMA Model Identification, Springer
<!--
R 時間序列
https://smac-group.github.io/ts/appendixb.html -->
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet