# Solving the TSP Problem: A Step-by-Step Journey

The challenge we faced was twofold:
1. **Regularizing the Map:**
Converting an irregular map (with U-turns, traffic rules, etc.) into a traditional graph with `(from, to, cost)` format.
2. **Solving the TSP:**
Finding the optimal tour through 40 points (waypoints) extracted from the map.

---

## 1. Regularizing the Map

Hazem tackled the core problem by transforming the map's complex structure into a **regular graph**.


Ahmed (Carla expert) contributed by:

- **Extracting Waypoints:**
Obtaining coordinates in the format `(x, y, z)`.

- **Generating Edges:**
Creating edges between all possible points with the format `(fromIdx, toIdx, path cost)`.
This captures the real-world costs, considering U-turns, traffic rules, and more.

*Visual Analogy:*
Imagine taking a chaotic city map and overlaying a neat grid where every intersection is connected by weighted roads.

---

## 2. Building the Adjacency Matrix

Once we have the regular graph of 40 points, the next step is to compute the **adjacency matrix** which represents the minimum path cost between every pair of points.

For example, the matrix will look like this:

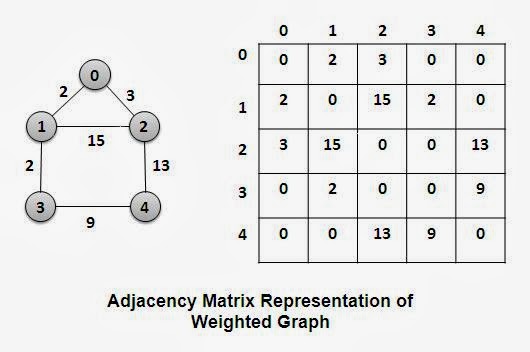
- **Using Dijkstra's Algorithm:**
We run Dijkstra’s algorithm from each of the 40 points to compute the shortest path cost to every other point.

---

## 3. Tackling the TSP Problem

### **The Challenge:**

- **Exact Solutions (DP):**
For 40 points, a Dynamic Programming (DP) solution using masks would require memory on the order of `N^2 * 2^N` (about 512 GiB), which is infeasible.

- **Heuristic Approach (Genetic Algorithm):**
We therefore opted for a genetic algorithm—a non-exact, heuristic solution that scales better for larger `N`.

### **Tuning the Genetic Algorithm:**

The performance of the genetic algorithm is highly sensitive to its parameters:

- `populationSize`
- `maxGenerations`
- `mutationRate`
- `crossoverRate`
- `tournamentSize`
- `earlyStoppingLimit`
- `useLocalSearch`
- `localSearchFrequency`
- `localSearchIntensity`

Our strategy was to:

1. **Store a Variety of Parameter Sets:**
We ran the TSP solver for each set of parameters.
2. **Select the Best Solution:**
By comparing the outputs, we pick the path with the minimal cost.

---

## 4. Testing and Accuracy

- **Benchmark with DP Masks:**
For smaller instances (`N < 25`), we implemented a DP solution with masks to obtain the correct path and cost.

- **Randomized Test Cases:**
We ran approximately 200 randomized tests. Initially, the genetic algorithm achieved around **75% accuracy** compared to the exact DP solution.

- **Goal:**
Fine-tune the parameters to push the accuracy as close as possible to **100%**.

---

## 5. Final Thoughts

By combining:
- A **regular graph transformation** of the map,
- An **all-pairs shortest path** calculation using Dijkstra’s algorithm,
- And a **genetic algorithm** (with extensive parameter tuning) for solving the TSP,

we created a robust and scalable solution for our problem.

> **Summary:**
> 1. Convert the irregular map into a regular graph.
> 2. Compute the all-pairs shortest paths to form the adjacency matrix.
> 3. Solve the TSP with a genetic algorithm and improve accuracy by exploring multiple parameter sets.

And finally, we are the .... soon !