---
tags: Společný základ
---
# SZ 6. Strojové učení
Strojové učení: Základní metody strojového učení (rozhodovací stromy včetně regresních, SVM, naivní Bayes, kNN). Semi-supervised learning a aktivní učení. Ansámblové učení. Základy analýzy anomálií. Pokročilé metody vyhodnocování experimentů (křížová validace, ROC křivky, AUC, M učících algoritmů na N datových sadách, bootstrapping). Teoretické základy strojového učení (relace generalizace ve výrokové a predikátové logice, prostor hypotéz a verzí, bias-variance trade off) (PV021, PV056)
Priprava na zkousku https://docs.google.com/document/d/1-XaEJr-zXcgS8zbEe3hMXlSxwWGb4lcKtHW7S3bO7V0/edit?usp=sharing
## Rozhodovací stromy
- Supervised neparametrická metoda pro klasifikaci a regresi
- Hlavní myšlenka
- vybudovat strom rozhodovacích pravidel, podle kterého vyvodíme predikci
- 
- Zdroje:
- https://www.saedsayad.com/decision_tree.htm
- [Scikit dokumentace](https://scikit-learn.org/stable/modules/tree.html)
- [KDnuggets](https://www.kdnuggets.com/2020/01/decision-tree-algorithm-explained.html)
- [Video - StatQuest klasifikace](https://www.youtube.com/watch?v=7VeUPuFGJHk)
- [Video - StatQuest regrese](https://www.youtube.com/watch?v=g9c66TUylZ4)
- [Video - StatQuest pruning](https://www.youtube.com/watch?v=D0efHEJsfHo)
### Klasifikační stromy
- **Jak vybudujeme strom?** (hlavní myšlenka)
- Strom budujeme iterativně shora (od kořene) hladovým přístupem
- Začneme s původní trénovací množinou
- V každé iteraci vypočítáme pro každý ještě nepoužitý atribut metriku, která
nám určuje, jak dobře atribut aktuální data rozděluje (chceme, aby se data
rozdělila na co "nejdisjunktnější" množiny)
- Vybereme nejlepší atribut podle zvolené metriky a rozdělíme podle něj data
na množiny
- Rekurzivně pokračuj v nově vytvořených množinách
- **Jaké metriky pro rozdělení existují (selection measure, splitting criterium)?**
- **Entropie**
- Měří "náhodnost" informací. Pokud je velká entropie, pak z informací nelze
odvodit žádné závěry.
- Chceme tedy vybrat atribut s co nejmenší entropii. Pokud bychom vybrali
atribut s velkou entropii, pak nám data rozdělí spíše náhodně.
- Příklad. Hod mincí
- 
- Pokud máme férovou minci, pak je entropie nejvyšší (1). Pokud ji máme
"cinklou", pak se entropie snižuje.
- Definice.
Nechť $X = (x_1, ..., x_n)$ je náhodná proměnná s pravděpodobnostní
distribucí $p_X(x)$. Pak
**(Shannonova) entropie** náhodné proměnné $X$ je definována jako
$$
Ent(X) = -\sum\limits_{x = 1}^n p_X(x) \log p_X(x)
$$
- **Informační zisk (information gain)**
- Je de facto mutual information (viz [Prob. in CS](https://hackmd.io/VX-jiFVER2SKks-Oys3_bQ#Mutual-information))
- Jednoduše řečeno měří zisk informací po rozdělení podle daného atributu
$$
Gain = Ent(before) - \sum^K_{j=1} Ent(j | after)
$$
, kde K jsou vzniklé podmnožiny
- Pro formálnější definici viz předchozí odkaz nebo [wiki](https://en.wikipedia.org/wiki/Information_gain_in_decision_trees)
- **Gini index**
- Statquest - https://youtu.be/7VeUPuFGJHk?t=428
- Měří jak často by byl náhodný element z množiny špatně klasifikován, pokud
by byl náhodně klasifikován podle distribuce kategorií v podmnožině
- Odečteme kvadrát pravděpodobností pro každou kategorii od jedničky
$$
Gini = 1 - \sum\limits^K_{i=1} p_i^2
$$
- Dělení podle numerických hodnot provedeme např. tak, že seřadíme data podle
daného numerického atributu. Zprůměrujeme každé dvě sousední hodnoty a ty použijeme jako threshold pro dělení.
- Další možné parametry zahrnují:
- maximální hloubka stromu
- minimální počet elementů v množině, aby došlo k rozdělení (pokud jich tam je
méně, bude se brát množina jako samostatný uzel)
- minimální počet elementů k vytvoření listu
- viz [scikit implementace](https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html#sklearn.tree.DecisionTreeClassifier)
### Regresní stromy
- Podobné jako klasifikační stromy, ale výstupem není diskrétní hodnota
(kategorie, label, ...), ale spojitá hodnota (float)
- Chceme odhadnout vztah mezi náhodnými veličinami. Např. účinnost vakcíny na
základě velikosti dávky. Chceme pak umět odhadnout účinnost, když modelu
předhodíme nějákou hodnotu dávky.
- Jako splitting criterion budeme používat metriky typická pro spojité veličiny:
- Střední kvadratická chyba (Mean squared error, MSE) a jeji varianty
$$
MSE(X) = \dfrac{1}{n} \sum\limits_{x \in X}(x - \bar{x})^2
$$
, kde $\bar{x}$ je výběrový průměr.
- Mean absolue error
- Poisson deviance
- Musíme tedy pro každý atribut a jeho hodnoty vypočítat MSE a vybrat takovou
dvojici (atribut, hodnota), která má nejmenší MSE.
- Příklad. Aproximace sinu pro různé parametry maximální hloubky stromu
- 
### Jak zamezit overfittingu?
- Můžeme stromy prořezat (odstranit větve):
- Preprunning označuje prořezávání při budování stromu, tedy typicky máme
zvolenou maximální hloubku stromu
- Postpruning označuje prořezávání po vybudování stromu
- Nejběžnější algoritmus je Minimal Cost-Complexity Pruning
- Víceméně používáne dodatečnou metriku, kterou počítáme pomocí validačího
datasetu. Projdeme strom buď bottom-up nebo top-down podle metody a
nahrazujeme podstromy listy, pokud platí nějaká podmínka
- Random forest
### Výhody a nevýhody
#### Výhody
- Jednoduché na pochopení a interpretaci. Lze je snadno vizualizovat.
- Jsou neparametrické. Nepředpokládáme žádné vlastnosti o datech.
- Rychlé pro inferenci.
#### Nevýhody
- Snadno se overfitujou.
- Jsou nestabilní ve smyslu, že malé změny můžou ovlivnit velkou část struktury
stromu.
## Support vector machine (SVM)
- Supervised klasifikační a regresní metoda
- Hlavní myšlenka:
- 
- Najít takovou **nadrovinu**, která nám rozumně rozdělí data (např. pro
klasifikaci)
- Nadrovina v $n$-té dimenzi je jeho jakýkoliv podprostor o $n-1$-dimenzi
tj. v 2D rovině je nadrovinou každá přímka, v 3D prostoru to je každá
rovina, apod.
- Intuitivně taková nadrovina má nejdelší vzdálenost mezi "hraničními"
příklady různých kategorií, kterým říkáme **support vectors** (na obrázku jsou
zvýrazněny v kolečku). Tomuto ohraničenému prostoru říkáme **margin**. Pokud
margin nepovoluje misklasifikace, pak mluvíme o **hard margin**. Reálně
misklasifikace do jisté míry povolujeme (dané nějakým parametrem) a říkáme
mu **soft margin**.
- Tedy **cílem je minimalizace** nějaké **loss funkce**, která nám popisuje kvalitu
soft marginu.
- Pokud $n$-dimenzionální data nejsou lineárně separovatelné
$n$-dimenzionální nadrovinou, **transformujeme data do vyšší dimenze**, kde už
data lineárně separovatelné jsou
- Způsob transformace nám udává **kernelová funkce** (nebo prostě
**kernel**).
- Příklady kernel funkcí:
- **Polynomiální**
- Dána parametrem určující stupeň polynomu (cílová dimenze).
- **Radial basis function**
- "Transformuje" data do nekonečné dimenze.
- V praxi data **reálně netransformujeme**, ale umíme vypočítat skalární součin ve vyšší dimenzi bez transformace. Tomuto způsobu říkáme
**kernel trick**.

- Matematika:
- Doporučuju tento [článek](https://shuzhanfan.github.io/2018/05/understanding-mathematics-behind-support-vector-machines/)
- **Skalární součin** pro $\vec{x} \in \mathbb{R}^n$ a $\vec{y} \in \mathbb{R}^n$ je
$$
\vec{x} \cdot \vec{y} = \sum\limits^n_{i=1}x_i y_i
$$
- **Přímka** je $y = ax+b$. Přejmenujeme $x \mapsto x_1$ a $y \mapsto x_2$. Tedy
máme
$$
\begin{array}{rl}
x_2 &= ax_1 + b \\
ax_1 - x_2 + b &= 0
\end{array}
$$
Definujme $\vec{x} = (x_1, x_2)$ a $\vec{w} = (a, -1)$. Dostaneme pak
$$
\vec{w} \cdot \vec{x} + b = 0
$$
Tohle platí i pro vyšší dimenze. Takže je toto rovnice pro **nadrovinu**.
- **Klasifikátor** parametrizovaný váhami $\vec{w}$ pro labely $\{-1, 1\}$
definujeme jako
$$
y[\vec{w}](\vec{x}) =
\begin{cases}
+1 & \text{jestliže } \vec{w} \cdot \vec{x} + b \geq 0\\
-1 & \text{jestliže } \vec{w} \cdot \vec{x} + b < 0\\
\end{cases}
$$
nebo zjednodušeně pomocí funkce signum $sgn(x) = \begin{cases}
+1 & \text{jestliže } x \geq 0\\
-1 & \text{jestliže } x < 0\\
\end{cases}$
$$
y[\vec{w}](\vec{x}) = sgn(\vec{w} \cdot \vec{x} + b)
$$
- **Eukleidovskou normu** vektoru $\vec{x} \in \mathbb{R}^n$ definujeme jako
$$
\left\lVert x\right\rVert = \sqrt{x_1^2 + ... + x_n^2}.
$$
Norma udává vzdálenost od počátku.
- Máme tedy klasifikátor, který je dán váhami $\vec{w}$. Kouknem se na
geometrický význam. Vektor $\vec{w}$ je vektorová normála nadroviny (je k ní
kolme) $\vec{w} \cdot \vec{x} + b = 0$. Viz 2D příklad dole. Je to zatím
naprosto stejné jako [geometrický význam neuronu](https://is.muni.cz/auth/el/fi/podzim2020/PV021/um/neuron-geometry.png?1610806521518).

- Signed vzdálenost bodu $\vec{u}$ od nadroviny se vypočítá jako
$$
\dfrac{\vec{w} \cdot \vec{u} + b}{\left\lVert \vec{w}\right\rVert}
$$
- Support vektory $\vec{x}_{sv}$ jsou ty body, které mají nejmenší vzdálenost od hledané
dělící nadroviny. Chceme tedy maximalizovat margin $M$, což je dvojnásobek
vzdálenosti support vektorů od hledané dělící nadroviny:
$$
M = 2 \cdot \dfrac{|\vec{w} \cdot \vec{x}_{sv} + b|}{\left\lVert \vec{w}\right\rVert}
$$
Jak ale poznáme, že dělící nadrovina správně klasifikuje? Použijeme výsledek
z klasifikátoru a zavedeme si podmínku, které musíme splnit při maximalizaci.
$$
M = 2 \cdot \dfrac{y[\vec{w}](\vec{x}_{sv}) \cdot (\vec{w} \cdot \vec{x}_{sv} + b)}{\left\lVert \vec{w}\right\rVert}
$$
pro $y[\vec{w}](\vec{x}_{sv}) \cdot (\vec{w} \cdot \vec{x}_{sv} + b) \geq 1$
- Maximalizace tohoto výrazu je ekvivalentní maximalizování
$$
\dfrac{2}{\left\lVert \vec{w}\right\rVert}
$$
(nebo minimalizování $\dfrac{\left\lVert \vec{w}\right\rVert}{2}$)
- Dále jde uvedená maximalizace přeformulovat na kvadratický optimalizační
problém tj.
$$
\min \phi(\vec{w}) = \left\lVert \vec{w}\right\rVert^2 = \vec{w} \cdot \vec{w}
$$
a musí platit pro všechny support vektory
$$
y[\vec{w}](\vec{x}) \cdot (\vec{w} \cdot \vec{x} + b) \geq 1
$$
- Tento problém se řeší pomocí **kvadratického programování**.
- Zbytek TODO (to už je fakt teorie optimalizací a operátorů 😢)
- Ne nutně, co jsem našel já, tak se to dá řešit metodou Lagrangeových mutiplikátorů.
- Viz:
- [Video: StatQuest SVM playlist](https://youtube.com/playlist?list=PLblh5JKOoLUL3IJ4-yor0HzkqDQ3JmJkc)
- [SciKit SVM dokumentace](https://scikit-learn.org/stable/modules/svm.html)
- [SVM Wiki](https://en.wikipedia.org/wiki/Support-vector_machine)
- [Kernel metody Wiki](https://en.wikipedia.org/wiki/Kernel_method)
- [IB031 slajdy](https://is.muni.cz/auth/el/fi/jaro2018/IB031/um/svm.pdf)
- [Kniha: Pattern Recognition and ML, Ch. Bishop, Kapitola 7](https://www.microsoft.com/en-us/research/uploads/prod/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf)
### Výhody a nevýhody
#### Výhody
- Efektivní na vícedimenzionální data díky kernel trickům.
- Všestranný díky tomu, že můžeme definovat různe typy kernel funkcí.
- Pokud jsou data jasně separovaná, pak je SVM velmi efektivní.
#### Nevýhody
- Standardní SVM nevrací pravděpodobnosti pro své predikce. Ty se musí dopočítat
pomocí drahých metod.
- Náchylné na šum v datech.
- Na velkých datech se trénuje relativně dlouho. Nehodí se na velká data.
## Naivní Bayes
- Supervised klasifikační metoda
- Terminologie
- Nechť $X = (X_1, ..., X_n)$ je **náhodný vektor**, kde $X_i$ je **náhodná
veličina**.
- **Sdružená pravděpodobnost** náhodného vektoru $X$ je dána všemi kombinacemi
hodnot náhodných veličin $X$ tj. $p_X(x_1, ..., x_n) = P(X = (x_1
,\dots, x_n)) = P(X_1=x_1\wedge ... \wedge X_n=x_n)$ pro všechny různé $x=(x_1, ..., x_n)$.
- Pokud pracujeme s malým počtem náhodných veličin, lze sdruženou
pravděpodobnost zobrazit v tabulce. Mějme náhodný vektor složený ze dvou
náhodných veličin $X$ a $Y$:

- **Marginální pravděpodobnost** je pravděpodobnost, že daná náhodná veličina
nabývá konkrétní hodnoty tj. např. $p_{X_i}(x_i) = P(X_i = x_i)$. To se rovná
součtu všech dílčích sdružených pravděpodobností, kde $X_i = x_i$. Tzn. např.
pro $Y = 2$ v tabulce sečteme hodnoty v příslušném sloupci.
- **Podmíněná pravděpodobnost** dvou náhodných proměnných $X$ a $Y$, $P(X|Y)$, je
podmíněná pravděpodobnost $P(X=x|Y=y)$ pro všechny různá $x$ a $y$:
$$
P(X|Y=y) = \dfrac{p_{XY}(x, y)}{p_Y(y)} \text{ pro všechny hodnoty } x
$$
$p_{XY}$ je sdružená pravděpodobnost náhodných veličin $X$ a $Y$. $p_Y(y)$
je marginální pravděpodobnost.
- **Bayesův klasifikátor**. Mějme náhodnou veličinu $C$, která bude
reprezentovat $K$ kategorií. $X = (X_1, \dots, X_n)$ bude náhodný vektor o $n$
náhodných veličinách popisující nějáke atributy (features). Chceme predikovat
nejpravděpodobnější kategorii na základě daných atributů $(x_1, ..., x_n)$ tj.
$$
\mathrm{argmax}_{i\in\{1,...,K\}} P(Y = y_i | X = (x_1, \dots, x_n))
$$
- Jak ale vypočítáme $P(Y = y_i | X = (x_1, ..., x_n))$? Podle definice
$$
P(Y = y_i | X = (x_1,...,x_n)) =
\dfrac{p_{YX_1,...,X_n}(y_i, x_1, ..., x_n)}{p_{X_1,...,X_n}(x_1,...,x_n)}
$$
Museli bychom si pro hodnoty sdružené pravděpodobnosti udržovat šíleně
velkou tabulku. Pokud bychom jen do té příkladové tabulky chtěli přidat
náhodnou veličinu, která nabývá třech různých hodnot, měli bychom 3x více
hodnot. Konkrétně pokud $n$ náhodných veličin jsou binární, pak potřebujeme
$2^n$ hodnot pro $P(Y = 0 | X = (x_1, ..., x_n))$ pro **každé různé**
$(x_1, ..., x_n)$. Musíme na to jinak.
- **Bayesova věta**. Zkusíme podmíněnou pravděpodobnost obrátit pomocí
Bayesovy věty.
$$
P(Y = y | X = (x_1, ..., x_n)) =
\dfrac{P(Y=y) \cdot P(X = (x_1, ..., x_n)|Y=y_i)}{P(X = (x_1, ..., x_n))}
$$
- Nyní musíme vypočítat **prior** $P(Y=y)$ pro každé $y$ a
**conditionals/likelihood** $P(X = (x_1, ..., x_n)|Y=y)$.
- $P(Y = y)$ lze odhadnout z dat. Prostě použijeme relativní četnost.
Mějme data o velikosti $p$ a počet příkladů $n_i$, které jsou v kategorii
$y_i$
$$
P(Y = y_i) = \dfrac{n_i}{p}
$$
- $P(X = (x_1, ..., x_n)|Y=y)$ má stále mnoho hodnot, aby to bylo šlo
prakticky odhadnout.
- **Budeme (naivně) předpokládat, že náhodné veličiny jsou podmíněně
nezávislé**.
Platí pak
$$
\begin{array}{rl}
P(X|Y) &= P(X_1, ..., X_n | Y) = P(X_1 | Y) \cdot P(X_2 | Y) \cdot ...
\cdot P(X_n | Y) \\
&= \displaystyle\prod\limits^n_{i=1}P(X_i | Y)
\end{array}
$$
Takže teď pouze potřebujeme odhadnout $P(X_i = x_{i} | Y = y)$ pro
každou možnou hodnotu $X_i$ a kategorii $Y$.
- Máme tedy klasifikátor
$$
\mathrm{argmax}_{i\in\{1,...,K\}} \dfrac{P(Y=y_i) \cdot \displaystyle\prod\limits^n_{j=1}P(X_j = x_j | Y=y_i)}{P(X = (x_1, ..., x_n))}
$$
- Jmenovatel $P(X = (x_1, ..., x_n))$ je dán vstupem a je tedy pro
všechny kategorie konstantní a nemusíme ho odhadovat. To je ekvivalentní
odhadu **Maximum a posteriori (MAP)**.
- Pokud nám nezáleží na $P(Y = y_i)$ nebo je uniformní, pak je
Bayesův klasifikátor ekvivalentní s **Maximum likelihood estimation (MLE)**
$$
\mathrm{argmax}_{i\in\{1,...,K\}} P(X = (x_1, ..., x_n) | Y = y_i )
$$
- **Problém**. Může se stát, že nějaká hodnota atributu se v trénovacích
datech nevyskytne. Pak $P(X_i = x_{i} | Y=y) = 0$. Tím pádem bude všechno $0$.
- Řešení. Normalizujeme pravděpodobnosti tak, ať jsou nenulové. Např.
Laplace smoothing
- 
- Příklad.
- 
- 
- Viz
- [IB031 slajdy](https://is.muni.cz/auth/el/fi/jaro2018/IB031/um/probabilistic-classification.pdf)
- [Scikit docs](https://scikit-learn.org/stable/modules/naive_bayes.html)
- [Wiki](https://en.wikipedia.org/wiki/Naive_Bayes_classifier)
## kNN
## Semi-supervised learning
- Motivace:
- Anotace dat je drahá
- Ruční anotace je časově náročná a nákladná.
- Někdy potřeba expertů (anotace medicínských dat).
- Řešení:
- Použít oboje neanotované i anotované data k vytvoření modelu. Jedná se tedy
o přístup na pomezí supervised learning a unsupervised learning.
- Obecný přístup:
- Natrénujeme model pomocí anotovaných dat.
- Uděláme predikci na neanotovaných datech.
- Nejlepší predikce přiřadíme k anotovaným datům (někdy říkáme, že to jsou
pseudo anotace/labely)
- Natrénujeme znovu s pseudo anotacemi a opakujeme proces.
- 
Konkrétní metody
- [Self-training algorithm](https://towardsdatascience.com/self-training-classifier-how-to-make-any-algorithm-behave-like-a-semi-supervised-one-2958e7b54ab7)
- předpoklad: pokud má model vysokou confindence v label, asi je správně
- můžeme olabelovat
- nejvíce confident
- všechny
- všechny ale váženě podle confidence
- jednoduché
- dá se lehce přidat na existující classifiery
- NLP aplikace
- brzké chyby se propagují dál
- Generativní modely
- TODO pls zkontrolovat (Davide, ty si expert na generativní modely)
- spočítá se decision boundary a pak se podle ní olabelují data
- neolabelovaná data se berou v potaz při počítání boundary
- 
- Semi-supervised SVM
- assumption: neolabelovaná data různých class jsou separovány velkým marginem
- zkusí všechny možné olabelování dat a vybere takové, které má největší SVM margin
- můžeme aplikovat všude kde SVM
- těžká optimalizace, lokální minima
- Graph-based algoritmy
- assumption: instance spojené výraznou hranou mají stejný label
- graf olabelovaných i neolabelovaných dat
- hrany značí nejakou similarity??
- 
## Aktivní učení
- Motivace podobná jako u semi-superivsed learningu.
- Model se dotazuje na chybějící anotace orákla (může být např. člověk nebo
ensemble modelů tzv. query by commitee).
Dotazuje se např. na ta data, u kterých si není velmi jistý.
- 
- Máme typicky pool nějakých neolabelovaných samplů.
- Zeptáme se na ty, kde jsme si nejmíň jistí.
- to může být podle největší entropie, nejmenší confidence, nebo nejmenšího marginu.
## Ansámblové učení
- [Odkaz na slajdy](https://is.muni.cz/auth/el/fi/jaro2019/PV056/um/62776009/68579165/ml-ensembles.pdf)
- Hlavní myšlenka:
- Využití dvou a více modelů pro predikci.
- Výhody:
- Ansámbly jsou typicky přesnější a robustnější než samostatné modely.
- Snadná paralelizace.
- Nevýhody:
- Výpočetně náročnější.
- Neefektivní pro nekvalitní data.
- Do jisté míry ztráta možnosti interpretace modelu.
- Viz
- [Scikit docs](https://scikit-learn.org/stable/modules/ensemble.html)
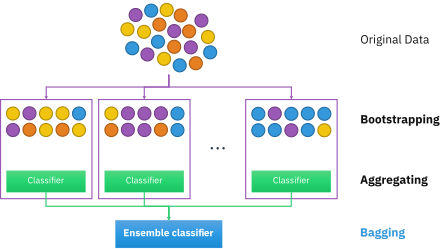
### Bagging
- Aka **b**ootstrap **agg**regat**ing**
- Hlavní myšlenka:
- Budeme mít $n$ modelů.
- Bootstrapping fáze. Uděláme $n$ tzv. bootstrap vzorků z tréninkového datasetu. Ve vzorcích se můžou data opakovat (**vzorkování s opakováním**). Standardně
je **velikost jednoho vzorku stejná jako velikost původního tréninkového datasetu**.
Pokud je tréninkový dataset dostatečně velký, pak má jeden vzorek v průměru
~63.2% unikátních dat.
- Aggregating fáze. Každému vzorku přiřadíme model, který bude natrénovaný
na daném vzorku.
- Výstup:
- Regrese: zprůměrování výsledné hodnoty
- Klasifikace: hlasování (např. majority voting, tzn. výsledek, je to co,
predikovalo nejvíce modelů)
- 
- Data, která se nedostala do vzorků se nazývají **out-of-bag** data a mohou
být použita pro evaluaci modelu.
- Často se používá v kombinaci s rozhodovacími stromy.
#### Náhodné lesy (Random forests)
- Náhodné lesy využívají myšlenky baggingu.
- Vytvoříme ensemble z dvou a více rozhodovacích stromů.
- Kromě baggingu navíc využíváme **feature baggingu** tzn., že při splitovacím
kroku při budování rozhodovacího stromu náhodně vybereme podmnožinu features, ze
kterých vybíráme dělící uzel.
- Viz
- [Video StatQuest Random forests p1](https://www.youtube.com/watch?v=J4Wdy0Wc_xQ)
- [Video StatQuest Random forests p2](https://www.youtube.com/watch?v=sQ870aTKqiM)
### Boosting
- Hlavní myšlenka:
- Slabé modely (např. nějčastěji velmi malé stromy) natrénujeme sekvenčně.
- Každý další model se soustřeďuje na chyby předešlého modelu. Tzn. že snížíme
váhy u správně predikovaných dat a zvýšíme je u špatných predikcí u
předešlého modelu.
- Výstup se v tomhle případě také zprůměruje nebo odhlasuje za použití
naučených vah.
- 
- Nejzákladnější algoritmus je AdaBoost.
- Viz [Video StatQuest AdaBoost](https://youtu.be/LsK-xG1cLYA)
#### Gradient boosting
- AdaBoost se da zobecnit na tzv. **gradient boosting**.
- Trénujeme **silnější** (tedy jsou větší než u AdaBoostu) modely v závislosti na minimalizaci nějaké diferenciovatelné loss funkce. Tedy za využití gradientního
sestupu.
- Tím, že si můžeme loss funkci zvolit, jsou gradient boosting metody flexibilní.
- Viz
- [Video StatQuest Gradient Boosting](https://youtube.com/playlist?list=PLblh5JKOoLUJjeXUvUE0maghNuY2_5fY6)
- Populární knihovny:
- [XGBoost](https://xgboost.ai/)
- [LightGBM](https://github.com/microsoft/LightGBM)
- [CatBoost](https://catboost.ai/)
## Základy analýzy anomálií
- Metody
- Statistické
- Data jsou běžně generovány nějákým statistickým (stochastickým) modelem.
Pokud v množině existují data s malou pravděpodobností, že byly
vygenerovány modelem, pak jsou outliers.
- Proximity-based (blízkost)
- Založeno na vzdálenosti od ostatních objektů.
- Často se počítá pomocí hustoty objektů v okolí nebo shluků.
- Dále můžeme dělit podle:
- Supervised
- Převedeme na klasifikační problém, kdy máme kategorii "outlier".
- Unsupervised
- Častější. Předpokládáme, že většina dat je "normálních" a outlierů se tam
nebude vyskytovat hodně.
- Příklady
- 
- Local Outlier Factor
- 
- The local outlier factor is based on a concept of a local density, where locality is given by k nearest neighbors, whose distance is used to estimate the density. By comparing the local density of an object to the local densities of its neighbors, one can identify regions of similar density, and points that have a substantially lower density than their neighbors. These are considered to be outliers.
- IsolationForest
- Since recursive partitioning can be represented by a tree structure, the number of splittings required to isolate a sample is equivalent to the path length from the root node to the terminating node.
- This path length, averaged over a forest of such random trees, is a measure of normality and our decision function.
- Random partitioning produces noticeably shorter paths for anomalies. Hence, when a forest of random trees collectively produce shorter path lengths for particular samples, they are highly likely to be anomalies.
- Využití:
- Detekce podvodů
- Medicína (neobvyklé symptomy apod.)
- Chyby v měření
- Viz
- [Scikit docs](https://scikit-learn.org/stable/modules/outlier_detection.html)
- [PV056 slajdy](https://is.muni.cz/auth/el/fi/jaro2019/PV056/um/62159239/Class_Outlier_Detection-Porto-May13-2014-3.pdf)
## Pokročilé metody vyhodnocování experimentů
### Křížová validace
- Motivace
- Normálně používáme trénovací a testovací dataset. Jak ale zaručíme, že
testovací dataset bude vhodně vyvážený (např. máme málo dat a hrozí, že ho
špatně navzorkujeme)?
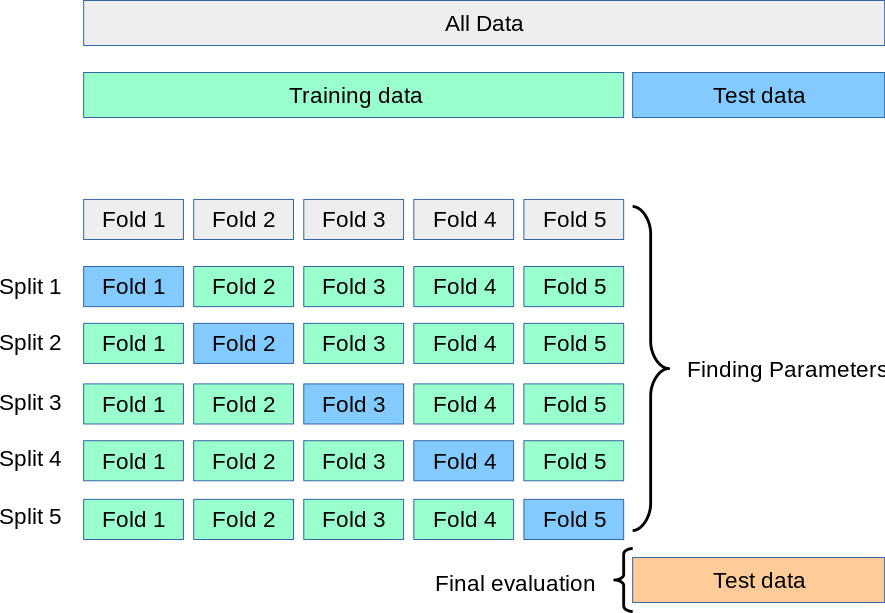
- Hlavní myšlenka:
- Použijeme celý dataset, který rozdělíme na $k$ částí ($k$-fold cross
validation). Jednu použijeme na testování a zbytek na trénování. Postupně tak
vystřídáme testovací část za další a zprůměrujeme chybu/kvalitu modelu.
- Často se využívá pro hledání optimálních hyperparametrů. Kdybychom měli
optimalizovat pouze na jednom testovacím datasetu, tak pak na něm overfittujeme.
Je proto vhodné použít křížovou validaci:
- 
- Ze statistického hlediska je tento způsob evaluace lepší než mít pouze
jednu testovací sadu. Ovšem křížová validace bude výpočetně náročnější.
### ROC křivka, AUC
- Mějme binární klasifikační problém a chceme evaluovat výkon modelu a případně
stanovit optimální threshold pro klasifikaci.
- AUC je plocha pod ROC křivkou.

### Confusion matrix (matice záměn)
- 
#### True positive rate (senzitivita)
$$
\text{TPR} = \dfrac{TP}{P} = \dfrac{TP}{TP+FN}
$$
#### True negative rate (specificita)
$$
\text{TNR} = \dfrac{TN}{N} = \dfrac{TN}{TN+FP} = 1 - FPR
$$
#### False positive rate (fall-out)
$$
\text{FPR} = \dfrac{FP}{N} = \dfrac{FP}{FP+TN} = 1 - TNR
$$
### ROC křivka a AUC
- Zkoumáme vztah TPR vůči FPR na různých hladinách thresholdu pro klasifikaci
(každá hodnota je klasfikátor s jinak nastavenou threshold hodnotou)
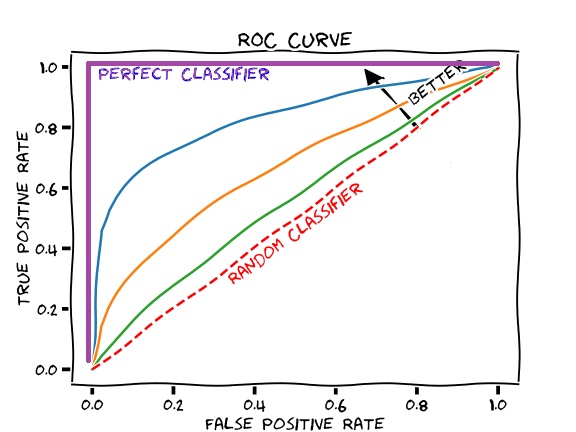
- ❗ Bacha, někdy se dává dolů specificita (TNR), ale hodnoty jdou od 1 po 0.
Tvar křivky je ale stejný.)
- Křivku můžeme interpretovat pomocí **AUC (area-under-curve)**, která vyjadřuje
obsah pod ROC křivkou. Čím větší AUC, tím lepší model.
- [Video StatQuest](https://youtu.be/4jRBRDbJemM)
### M učících algoritmů na N datových sadách
- Otázka směřuje na porovnání různých modelů pomocí statistických testů
- Pokud porovnáváme více učících algoritmů (např. Naive Bayes, Decision Trees, Neural Net) na 1 datasetu, můžeme využít cross-validace:
- dataset rozdělíme na $n$ foldů, například 10
- pomocí učícího algoritmu nafitujeme model vždy na $(n-1)$ foldech a na zbylém změříme accuracy, propermutujeme tak aby každý fold byl jednou ten testovací
- měření accuracy na foldech chápeme dohromady jako 1 statistický výběr
- párovým T-testem můžeme porovnat dva algoritmy (uděláme rozdíly a testujeme hypotézu H0, že rozdíl je 0)
- to nám dá tabulku:
| Fold | NB - DT | NB - NN | DT - NN |
|------|-----------|-----------|-----------|
| 1 | -0.0715 | -0.0355 | 0.0361 |
| 2 | -0.1947 | -0.1866 | 0.0081 |
| 3 | 0.0209 | -0.1398 | -0.1607 |
| 4 | -0.2189 | 0.0088 | 0.2277 |
| 5 | -0.1424 | -0.1265 | 0.0159 |
| 6 | -0.1739 | -0.2065 | -0.0325 |
| 7 | 0.0992 | 0.0204 | -0.0788 |
| 8 | -0.0371 | 0.2255 | 0.2626 |
| 9 | -0.2802 | -0.2700 | 0.0102 |
| 10 | 0.0341 | 0.0410 | 0.0069 |
| **avg** | -0.0965 | -0.0669 | 0.0295 |
| **stdev** | 0.1246 | 0.1473 | 0.1278 |
| **p-value** | **0.0369** | 0.1848 | 0.4833 |
- $\rightarrow$ zamítáme hypotézu že NB a DT performují stejně
- pokud porovnáváme na rozdílných datových sadách a ne na foldech jednoho datasetu, nemůžeme použít T-test, protože ten předpokládá že jednotlivá měření pocházejí ze normální distribuce
- použijeme neparametrické testy, mají méně předpokladů
- vhodný je Wilcoxonův párový test, který testuje, že medián rozdílu je nulový
- rozdíly v accuracy seřadíme podle absolutní hodnoty, potom záporné rozdíly obarvíme modře, kladné červeně
| Dataset | NB - DT | Rank |
|----------|-----------|---------------|
| 1 | -0.0715 | <span style="color:blue;">4</span> |
| 2 | -0.1947 | <span style="color:blue;">8</span> |
| 3 | 0.0209 | <span style="color:red;">1</span> |
| 4 | -0.2189 | <span style="color:blue;">9</span> |
| 5 | -0.1424 | <span style="color:blue;">6</span> |
| 6 | -0.1739 | <span style="color:blue;">7</span> |
| 7 | 0.0992 | <span style="color:red;">5</span> |
| 8 | -0.0371 | <span style="color:blue;">3</span> |
| 9 | -0.2802 | <span style="color:blue;">10</span>|
| 10 | 0.0341 | <span style="color:red;">2</span> |
- součet pořadí kladných rozdílů je <span style="color:red;">$1+5+2=7$</span>, součet pořadí záporných rozdílů je <span style="color:blue;">$4+8+9+6+7+3+10=47$</span>
- Porovnáme menší z nich (tedy <span style="color:red;">$7$</span>) s tabulkovou hodnotou pro Wilcoxonův test. Intuitivně by měly být součet obou pořadí podobné pokud jsou učící algoritmy stejně dobré.
### Bootstrapping
- Bootstrapping je obecně metoda založena na vzorkování s opakováním na rozdíl
od klasické křížové validace, která s opakováním nevzorkuje.
- Můžeme tedy model evaluovat podobně jako u křížové validace, ale budeme
vzorkovat s opakováním.
- Křížová validace je méně biased, ale má vyšší variance. U bootstrapping
je to naopak (jsou pesimističtější) [(1)](https://stats.stackexchange.com/questions/18348/differences-between-cross-validation-and-bootstrapping-to-estimate-the-predictio).
## Teoretické základy strojového učení
### Relace generalizace ve výrokové a predikátové logice, prostor hypotéz a verzí
- Viz [Výpočetní logika - induktivní inference](https://hackmd.io/@uizd-suui/rJYiFUvM8#Induktivn%C3%AD-inference-ve-v%C3%BDrokov%C3%A9-a-predik%C3%A1tov%C3%A9-logice)
- Relace generalizace v predikátové logice:
- Formule $\varphi$ je generalizace formule $\psi$ iff
platí $\varphi \vDash \psi$.
- Tj. v každé interpretaci, kde je $\varphi$ pravdivá, je $\psi$ také pravdivá.
Nebo také: množina interpretací, kde $\varphi$ je pravdivá, je podmnožinou
interpretací, kde je $\psi$ pravdivé (tj. $\psi$ má více restrikcí a je
specifičtější).
### Bias-variance trade off
- Bias
- **Vysoký** bias modelu znamená, že model nedokáže dobře popsat data (**underfitting**).
- Variance
- **Vysoký** variance modelu znamená, že model je příliš senzitivní a
zachycuje náhodný šum (**overfitting**).
- Chceme mít nízký bias a nízkou varianci.
- Oba parametry jsou ovšem v trade-off vztahu. Tedy, pokud snížíme bias, tak se
typicky zvyšuje variance a naopak.
- 
- [Video Statquest](https://www.youtube.com/watch?v=EuBBz3bI-aA)