# Gates & Circuit

Trước khi bắt đầu làm quen với các phần cứng như RAM, CPU,..., chúng ta cần phải nắm rõ về những thứ cấu thành nên các linh kiện đó. Một thanh RAM không thể tự mình lưu trữ tất cả các thông tin như cách mà chúng ta cất đồ vào tủ, và CPU cũng không thể thực hiện được các phép toán mà thiếu đi các công cụ chuyên dụng của nó. Trong chương này, chúng ta sẽ nghiên cứu những khái niệm cơ bản nhất như đại số Boolean, các cổng logic, và sử dụng chúng để hình thành các dạng mạch logic cơ bản, vốn là những mảnh ghép nhỏ nhất hình thành những phần cứng được sử dụng trong máy tính bây giờ.

## 1. Giới thiệu về đại số Boolean:

Để làm một bài đại số thông thường , chúng ta thường phải tuân theo một số quy tắc. Những quy tắc này được sử dụng thông dụng đến nỗi ta thường quên luôn cả tên gọi của chúng. Nhưng chúng lại là nền tảng của toàn bộ thể loại toán học chúng ta biết bây giờ.
Quy tắc số $1$: Phép cộng và nhân có tính giao hoán. Nghĩa là ta có thể đổi chỗ vị trí của các kí hiệu hai bên dấu.
Và ngược lại phép trừ và chia không có tính giao hoán.
Ví dụ như khi bạn đổi $7 + 3$ thành $3 + 7$ thì nó đều ra kết quả là $10$ nhưng khi đổi $7 - 3$ thành $3 - 7$ lại ra hai kết quả hoàn toàn khác.
Quy tắc số $2$: Phép cộng và nhân cũng có tính liên kết.
Quy tắc số $3$: Phép nhân sẽ được phân phối trên phép cộng.
Và một đặc tính của đại số thông thường là nó luôn làm việc với những con số như số cân đậu phụ, số lượng con cánh cụt, khoảng cách một con tàu đi được hay số tuổi của thành viên trong gia đình. Boole đã sáng tạo ra một thể loại đại số cách ly khỏi những con số và khiến đại số trở nên trừu tượng hơn, và giờ chúng ta gọi đó là đại số Boolean. Trong đại số Boolean, một biến không thay thế cho một số mà thay thế cho một tập (class hay còn được gọi là set).
Gạt toán sang một bên, giờ nói về mèo đi. Một con mèo có thể là con đực hoặc con cái. Để thuận tiện hơn chúng ta dùng $M$ (male) để đại diện cho các con đực và $F$ (female) cho con cái. Hãy luôn nhớ rằng hai biến $M$ và $F$ này không đại diện cho số lượng con mèo. Số lượng con đực và con cái có thể thay đổi chỉ trong vài phút ví dụ như một em bé mèo mới sinh ra hay một chú mèo ra (đáng tiếc thay) qua đời. Các chữ cái hay còn gọi là biến đại diện cho tập hợp của các con mèo có cùng một đặc tính.
Chúng ta cũng có thể sử dụng những chữ cái để thay thế cho màu sắc của những chú mèo. Ví dụ như: $T$ (tan) đại diện cho những con mèo có màu nâu vàng, $B$ (black) cho những con màu đen, $W$ (white) cho màu trắng và $O$ (others) cho những màu còn lại (những con không trong tập $T$,$W$ hay $B$).
Và cuối cùng , mèo có thể bị triệt sản hoặc chưa bị triệt sản. Hãy dùng $N$ (neutered) để đại diện cho tập hợp những con đã bị triệt sản và $U$ (unneutered) để đại diện cho các con mèo chưa bị triệt sản.
Quay lại toán nào, như ta đã biết trong đại số thông thường dấu $+$ được dùng cho phép cộng và dấu x được dùng cho phép nhân. Trong đại số Boolean, dấu $+$ và x cũng được sử dụng nhưng nó lại mang một ý nghĩa hoàn toàn khác.
Dấu $+$ trong Boolean nghĩa là union(hợp) của hai tập. Nghĩa là nó sẽ tạo ra một tập mới chứa tất cả phần tử của tập thứ $1$ và thứ $2$. Ví dụ, $B + W$ biểu diễn một tập gồm tất cả con mèo màu đen hoặc màu trắng.
Kí hiệu x trong Boolean nghĩa là intersection(giao thoa) của hai tập. Một giao thoa của hai tập sẽ tạo ra một tập mới chứa tất cả phần tử nằm trong cả tập thứ nhất và hai. Ví dụ, $F$ x $T$ biểu diễn một tập gồm tất cả các con mèo cái(female) và có màu nâu vàng(tan).
Phép phân phối, tính liên kết và tính giao hoán vẫn được giữ nguyên trong đại số Boolean. Chỉ khác là thay vì nhân (x) được phân phối trên ($+$) thì ở Boolean , dấu $+$ được phân phối trên dấu nhân.
Để hoàn thiện đại số Boolean , ta cần thêm một số kí hiệu khác. Kí hiệu $1$ nghĩa là tất cả mọi thứ. Ví dụ như trong ví dụ về những con mèo ta đề cập ở trên, $1$ là tập hợp của toàn bộ con mèo. Nên ta dễ dàng nhận thấy:
Biểu thức trên nghĩa là hợp của các con mèo cái và mèo đực là toàn bộ các con mèo. Tương tự vậy, hợp của mèo đen, mèo trắng, mèo nâu vàng và các màu còn lại cũng là tập hợp của toàn bộ con mèo.
Và một cách khác nữa:
Kí hiệu $1$ cũng có thể được sử dụng cùng dấu $-$ biểu diễn một tập hợp của toàn bộ mọi thứ ngoại trừ một cái gì đó. Ví dụ:
Là tập hợp của toàn bộ các con mèo ngoại trừ mèo đực hay nói cách khác là chỉ gồm toàn mèo cái.
Một kí hiệu khác ta cần sử dụng ở đây là kí hiệu $0$. Trong đại số Boolean $0$ biểu diễn cho một tập hợp rỗng (không có phần tử nào). Ví dụ:
Bởi không có con mèo nào mang cả hai giới tính đực và cái.
Bây giờ, sau khi đã nắm rõ những kiến thức cơ bản, ta sẽ đi vào một ví dụ phức tạp hơn. Giả dụ một ngày bạn đi vào cửa hàng thú cưng và nói với ông chủ rằng "Tôi muốn một con mèo đực, đã bị triệt sản, màu trắng hoặc nâu vàng; hoặc một con mèo cái, đã bị triệt sản, mọi màu trừ màu trắng; hoặc một con mèo màu đen". Và ông chủ cửa hàng nói lại với bạn rằng: "Vậy là bạn muốn một con mèo thỏa mãn biểu thức sau:
đúng không ?" Và bạn nói "Đúng rồi đó!".
Để chứng thực rằng ông chủ nói đúng, bạn có thể quên đi ý tưởng hợp và giao thoa mà thay vào đó dùng OR thay cho dấu ($+$) và $AND$ thay cho dấu (x).Và hai từ này biểu đạt chính xác ý nghĩa của nó trong tiếng anh. Khi bạn hợp hai tập hợp lại thành một tập hợp mới, bạn đã chấp nhận các phần tử nằm trong tập này HOẶC ($OR$) tập kia. Và khi bạn sử giao thoa hai tập hợp, bạn chấp nhận tất cả phần tử nằm trong cả tập này VÀ ($AND$) tập kia. Thêm nữa , bạn có thể sử dụng $NOT$ để thay thế cho số $1$ được theo sau bởi dấu ($-$).Tóm lại:

+ Kí hiệu $+$ (trước đây đượ hiểu là hợp) bây giờ nghĩa là $OR$
+ Kí hiệu x (trước đây được hiểu là giao thoa) bây giờ nghĩa là $AND$
+ "$1 -$" (trước đây được hiểu là toàn bộ ngoại trừ cái gì) bây giờ là $NOT$

Nên giờ ta có thể diễn đạt công thức trên lại thành:
Biểu thức này đã đúng ý bạn muốn, hãy để ý dấu ngoặc đơn làm rõ ý muốn của bạn. Bạn muốn một con mèo nằm trong một hoặc ba tập sau:
Với công thức đã được viết ra, ông chủ có thể làm một việc gọi là kiểm tra Boolean. Bây giờ , tôi sẽ đưa bạn đến một dạng khác của Boolean, trong dạng này, các chữ cái sẽ không biểu diễn cho một tập nữa mà nó có thể được thay số vào như toán thông thường. Điều đặc biệt là ở đây, ta sẽ chỉ thay số $0$ hoặc số $1$ vào thôi. Số $1$ nghĩa là có , thỏa mãn tiêu chuẩn và $0$ là ngược lại.
Ví dụ nhé, bây giờ ông chủ mang ra một con mèo đực chưa bị triệt sản, màu nâu vàng. Đây là công thức biểu diễn một con màu thỏa mãn nhu cầu khách hàng:
và đây là công thức sau khi thay số vào:
Để ý rằng những chữ cái được thay số $1$ vào chỉ là $M$ và $T$ vì con màu là đực và có màu nâu vàng. Nó được đơn giản hóa thành $1$ con mèo thỏa mãn điều kiện và $0$ con mèo không thỏa mãn điều kiện. Hãy nhớ rằng chúng ta không cộng và nhân ở đây nhưng mà chúng ta có thể coi rằng chúng ta làm thế.
Dấu x ở đây sẽ cho ra kết quả như bảng sau:
Nói cách khác kết quả là $1$ khi và chỉ khi cả hai vế là $1$. Ta thấy kết quả này giống hệt với đại số thông thường. Và sau đây là một bảng tổng hợp lại nhỏ hơn và tinh tế hơn:

| **AND** | **0** | **1** |
| -------- | -------- | -------- |
| **0** | $0$ | $0$ |
| **1** | $0$ | $1$ |

<!--  -->
Dấu $+$ nghĩa là OR và các kết quả có thể của nó là:
Kết quả là 1 khi một trong hai vế là $1$. $OR$ cho kết quả gần như giống phép cộng thông thường, chỉ khác là $1 + 1 = 1$. Và nó cũng có thể được tổng kết vào một bảng sau:
| **OR** | **0** | **1** |
| -------- | -------- | -------- |
| **0** | $0$ | $1$ |
| **1** | $1$ | $1$ |

<!--  -->
Bây giờ, ta đã sẵn sàng để tính toán kết quả.
Kết quả là $0$ nghĩa là không, con mèo không phù hợp với nhu cầu khách hàng.
Tiếp theo, ông chủ mang ra một con mèo cái đã bị triệt sản màu xám(màu xám sẽ thuộc về tập hợp $O$(others)) và biểu thức của nó là:
Và ta tính được kết quả:
Và kết quả là $1$. Tuyệt một con mèo đã tìm được mái ấm của mình.
Tối đó, khi chú mèo yêu đang say giấc thì bạn lại nghĩ rằng có thể nối một vài công tắc và bóng đèn lại để giúp bạn kiểm tra xem còn những con mèo nào thỏa mãn điều kiện không.
Để bắt đầu thí nghiệm của mình, bạn nối bóng đèn với nguồn nhưng bạn dùng hai công tắc thay vì một:
Hai công tắc được nối tiếp nhau như trên. Nếu bạn đóng công tắc bên trái, sẽ không có gì xảy ra cả:
Và cũng tương tự với công tắc phải. Bóng đèn chỉ sáng khi cả hai công tắc đều được đóng:
Từ khóa quan trọng nhất ở đây là $AND$, cả hai công tắc cần được đóng để dòng điện có thể chạy trong mạch.
Từ đó ta có thể đưa ra bảng sau:

| Công tắc trái | Công tắc phải | Bóng đèn |
| ------------- | ------------- | ---------- |
| Mở | Mở | Không sáng |
| Mở | Đóng | Không sáng |
| Đóng | Mở | Không sáng |
| Đóng | Đóng | Sáng |

<!--  -->
Ta thấy $1$ công tắc luôn có $2$ trạng thái là đóng và mở nên ta có thể sử dụng bit ở đây. Bit $0$ nghĩa là công tắc đang mở và bit $1$ có nghĩa là công tắc đang đóng. Tương tự bóng đèn cũng có $2$ trạng thái là sáng(lit) được biểu diễn là $1$ và không sáng(not lit) được biểu diễn là $0$. Và ta đơn giản viết lại bảng trên:

| Công tắc trái | Công tắc phải | Bóng đèn |
| ------------- | ------------- | -------- |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

<!--  -->
Ta thấy vai trò của công tắc trái và phải là tương đương nhau, vậy nên ta có thể viết lại bảng trên như cách ta viết với bảng $AND$ và bảng $OR$:
<!--  -->

| Công tắc trong dòng | 0 | 1 |
| ------------------- | ---- | ---- |
| **0** | 0 | 0 |
| **1** | 0| 1 |

Và nó giống hệt bảng $AND$.
Mạch điện này đã diễn tả hoạt động của $AND$ trong đại số Boolean.
Bây giờ nhé, ta thử nối mạch điện theo một cách khác đi:
Hai công tắc trên được mắc song song với nhau, sự khác nhau giữa mạch này và mạch trước đó là bóng đèn sẽ sáng khi một trong hai công tắc được đóng.
Hoặc công tắc dưới:
Hoặc cả hai công tắc luôn:
Bóng đèn sáng khi hoặc là công tắc trên đóng hoặc là công tắc dưới đóng. Từ khóa ở đây là HOẶC ($OR$).
Tương tự như trên, ta cũng có bảng biểu diễn với từng cặp trạng thái của công tắc:

| Công tắc trái | Công tắc phải | Bóng đèn |
| -------- | -------- | -------- |
| Mở | Mở | Không sáng |
| Mở | Đóng | Sáng |
| Đóng | Mở | Sáng |
| Đóng | Đóng | Sáng |

<!--  -->
Và cũng tương tự với cách thay số $0$ và $1$:

| Công tắc trái | Công tắc phải | Bóng đèn |
| -------- | -------- | -------- |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |

<!--  -->
Và cũng không quan trọng khi hai công tắc bị đổi chỗ nên ta có thể viết gọi lại như sau:

| Công tắc mắc song song | 0 | 1 |
| -------- | -------- | -------- |
| **0** | 0 | 1 |
| **1** | 1 | 1 |

<!--  -->
Chắc hẳn bạn cũng có thể đoán được nó giống với bảng OR:

| OR | 0 | 1 |
| -------- | -------- | -------- |
| **0** | 0 | 1 |
| **1** | 1 | 1 |

<!--  -->
Hay nói cách khác hai công tắc mắc song song miêu tả sự hoạt động của OR trong đại số Boolean.
<!-- Quay lại ví dụ về những con mèo, ta đã có sẵn một biểu thức biểu diễn nhu cầu khách hàng:
Và giờ với kiến thức vừa đề cập ở trên, ta có thể vẽ một mạch điện biểu diễn biểu thức trên như sau(với hai công tắc mắc nối tiếp biểu diễn một cổng logic AND (được kí hiệu là x) và hai công tắc mắc song song biểu diễn cổng logic OR(được kí hiệu là $+$)):
Mỗi công tắc được đặt tên với một chữ cái tương tự như trong đại số Boolean ( nghĩa là NOT W hoặc 1 - W)
Hãy nhớ lại mà xem, đầu tiên chủ cửa hàng mang ra một con mèo đực màu nâu vàng chưa bị triệt sản. Vậy ta sẽ đóng những công tắc thỏa mãn lại:
Mặc dù M, T và NOT W đã được đóng lại, chúng ta vẫn không có con đường nào hoàn chỉnh để dẫn điện cho bóng đèn. Tiếp theo, ông chủ mang ra một con mèo cái màu trắng và đã bị triệt sản:
Và bóng đèn vẫn tắt. Cuối cùng ông chủ mang ra con mèo cái màu xám đã bị triệt sản:
Và nó là đủ để thắp sáng bóng đèn và chỉ ra rằng con mèo phù hợp với các điều kiện của khác hàng. -->

## 2. Cổng Logic:
$1$. Khái niệm:
<!-- Các cổng logic là bộ phận cơ bản của bất cứ một hệ thống điện tử nào. Chúng đóng vai trò thực hiện các phép toán logic cơ bản. Các thiết bị điện tử ta dùng đều được cấu tạo nên từ những cổng logic. Các cổng logic được kết hợp và hoạt động cùng nhau, tạo nên một hệ thống mạch hoàn chỉnh và đưa ra hay trả về một kết quả cụ thể, tuỳ thuộc vào các tín hiệu chúng nhận được từ đầu vào. Cổng logic là một mạch điện tử nhận một hoặc nhiều đầu vào (input) và chỉ cho ra duy nhất một đầu ra (output). Hầu hết các cổng điện tử nhận 2 input và đưa ra 1 output. Các cổng logic hoạt động dựa trên các phép toán Boolean, và luôn có 2 trạng thái nhị phân, $true$ và $false$. Giá trị 1 tương ứng với $true$, và giá trị 0 tương ứng với $false$. Tuỳ thuộc vào loại cổng, và cách mà các cổng logic được kết hợp với nhau mà kết quả có thể khác nhau. Ta có thể tưởng tượng cổng logic như là một công tắc, khi bật là 1, còn khi tắt là 0.
Có 7 kiểu cổng logic, đó chính là: **AND, OR, NOT, NAND, NOR, XOR, XNOR**. -->
Vào một thời kỳ xa xôi nào đó, khi mà những hệ thống máy tính sơ khai vào thế kỷ 20 chỉ là một ký ức mờ ảo, ai đó đã thực sự nghĩ rằng cổng logic (logic gates) được đặt tên theo Bill Gates, đồng sáng lập của công ty Microsoft. Không hẳn là vậy. Như chúng ta sẽ thấy, các cổng logic tương tự như cánh cổng dinh độc lập bị húc đổ vào năm 1945, hay như bao cánh cổng khác vậy. Cổng logic thực hiện nhưng công việc đơn giản như chặn hay dẫn các dòng điện chạy qua mạch điện.
Bạn sẽ nhớ rằng trong phần trước, bạn đến một cửa hàng thú cưng và nói “Tôi muốn một con mèo đực, đã thiến, có thể trắng hoặc nâu; hoặc một con mèo đực, thiến, màu gì cũng được trừ trắng; hoặc tôi sẽ lấy bất cứ con mèo nào có màu đen.” Yêu cầu này có thể được tóm gọn qua một phép toán Boolean:


và cũng có thể được biểu diễn qua mạch điện sau:


Một mạch điện như vậy còn được gọi là một mạng lưới (network), mặc dù ngày nay từ này được dùng để nói về sự kết nối của nhiều máy tính, hơn là sự kết hợp của nhiều công tắc.
Mặc dù mạch điện này chẳng có gì là không có ở thế kỷ 19, không ai thời ấy nhận ra rằng các toán tử Bôlean có thể được biểu diễn trực tiếp qua mạch điện. Sự tương đồng này không hề được khám phá ra cho tới những năm 1930, nổi bật nhất là Claude Elwood Shannon (sinh năm 1916), người đã viết ra luận án mang tiêu đề “A Symbolic Analysis of Relay and Switching Circuits”.
Trước năm 1938, mọi người đều biết rằng nếu bạn nối 2 công tác nối tiếp, cả 2 công tắc cần đóng lại để dòng điện có thể chạy qua, và nếu bạn nối 2 công tắc song song, thì 1 trong 2 công tắc cần được đóng lại. Tuy vậy, không ai như Shannon nhận ra rằng các kỹ sư điện có thể sử dụng các toán tử boolean để thiết kế mạch điện với nhiều công tắc. Cụ thể hơn, nếu bạn có thể đơn giản hoá phép toán boolean, bạn có thể đơn giản hoá mạng lưới mạch điện.
Ví dụ, bạn muốn miêu tả các đặc điểm của con mèo mà bạn muốn:


Ta có thể hoán vị toán tử ở phép AND (dấu nhân)


Để giải thích, tôi sẽ gọi 2 biến mới là X và Y:


Khi đó, ta có thể viết lại phép tính như sau:


Sau đó, ta có thể đặt X và Y trở lại. Để ý tằng biến N xuất hiện 2 lần trong phép tính. Như vậy, ta có thể nhóm N lại:


Và giờ ta đặt X và Y trở lại:


Phép tính này vẫn chưa nhìn đơn giản cho lắm. Tuy nhiên, ta có thể rút gọn đi 1 biến, đồng nghĩa với việc ít đi 1 công tắc. Đây là phép tính sau khi được biểu diễn qua mạch điện:


Thật ra thì, vẫn có quá nhiều công tắc trong mạch điện. Về lý thuyết, ta chỉ cần 4 công tắc để tạo ra “con mèo” lý tưởng cho bạn. Vì sao lại là 4? Mỗi công tắc là một bit. Bạn sẽ có một công tắc cho giới tính (tắt là đực, bật là cái), một công tắc nữa cho sinh sản (tắt là chưa thiến, bật là thiến), và 2 công tắc nữa để quyết định màu. Cho 4 màu tổng cộng (trắng, đen, nâu, và “còn lại”), và ta hiểu rằng 4 lựa chọn chỉ cần đến 2 bit, vì vậy bạn chỉ cần đến 2 công tắc màu. Ví dụ, muốn chọn trắng, cả 2 công tắc có thể tắt, bật một cái để chọn đen, bật cái còn lại cho nâu, và cả 2 cùng bật nếu chọn màu khác.
Hãy làm một cái bảng điều khiển chọn mèo. Bảng điều khiển bao gồm 4 công tắc đơn giản và 1 cái đèn.


Công tắc sẽ bật nếu nó được gạt lên, và tắt nếu nó được gạt xuống. Công tắc thứ ba có ký hiệu B (black) để ký hiệu màu đen, và công tắc thứ 4, ký hiệu là T (tan) tưởng trưng cho màu nâu. Bật cả 2 công tắc sẽ cho ra một màu khác, được ký hiệu là O (other). Gạt cả 2 xuống sẽ cho ra ký hiệu W (white), là trắng.
Trong thuật ngữ tin học, các công tắc chính là thiết bị đầu vào. Đầu vào (input) là thông tin quyết định cách xử lý thông tin của mạch điện. Trong trường hợp… này, các công tắc đầu vào tương ứng với 4 bit thông tin mô tả con mèo. Và thiết bị đầu ra (output) chính là bóng đèn. Bóng đèn sẽ được bật nếu như các công tắc mô tả con mèo phù hợp. Các điều kiện này đều thoả mãn với yêu cầu của bạn, vì vậy bóng đèn được bật.
Điều ta cần làm bây giờ là thiết kế một mạch điện.
Giống như các công tắc, các rơ le có thể được nối tiếp và song song để thực hiện các công việc đơn giản. Sự kết hợp của các rơ le như thế này được gọi là các cổng logic. Khi tôi nói rằng các cổng logic thực hiện công việc đơn giản, ý tôi là đơn giản nhất có thể. Các rơ le có một ưu điểm so với công tắc đó chính là nó có thể được kích hoạt bởi các rơ le khác thay vì bằng tay. Điều đó có nghĩa là các cổng logic có thể được kết hợp để thực hiện các công việc phức tạp hơn, ví dụ như các phép tính đơn giản trong toán học. Sau đây, tôi sẽ cách dùng các công tắc, bóng đèn, quả pin và các rơ le để làm ra một máy tính như sau:


Để ý rằng công tắc ở bên trái đang mở và bóng đèn đang tắt. Khi bạn đóng công tác, quả pin ở bên trát sẽ tiếp điện cho nam châm điện, và khi được kích hoạt, nam châm sẽ hút thanh sắt, chạm vào đầu còn lại của đoạn dây nối với bóng đèn.


Khi nam châm điện hút thanh sắt, ta có thể hiểu rơ le được kích hoạt. Khi công tắc mở, nam châm điện sẽ ngừng kích hoạt và thanh sắt trở về vị trí ban đầu.
Đây giống như là một cách gián tiếp để bật bóng đèn, và đúng là như vật. Nếu như ta chỉ nghĩ cách bật bóng đèn, ta hoàn toàn có thể bỏ hệ thống rơ le. Nhưng chúng ta không ở đây để nghĩ cách bật bóng đèn, mà vì một mục đích khác cao cả hơn.
Chúng ta sẽ dùng rất nhiêu rơ le trong chương này, vì vậy tôi muốn đơn giản hoá mạch điện này. Ta có thể loại bỏ một số dây nối bằng cách nối đất. Trong trường hợp này, mặt đất chỉ sự kết nối chung.


Và ta có thể ký hiệu quả pin bằng "V". Giờ đây, mạch điện sẽ nhìn như thế này:


Mạch điện trên có 2 nguồn điện và 2 mặt đất. Các nguồn điện (V) có thể nối với nhau và các mặt đất cũng vậy. Toàn bộ mạng lưới mạch điện và cổng logic trong phần này chỉ cần đến 1 cục pin duy nhất. Ví dụ, mạch điện trên có thể được vẽ lại như sau:


Mạch điện này vẫn chưa được rõ ràng cho lắm. Sẽ tốt hơn nếu như ta tránh những mạch vòng và chỉ nhìn vào các rơ le – giống như bảng điều khiển ở trước đó – về mặt đầu vào và đầu ra:


Nếu như một dòng điện chạy qua đầu vào, nam châm điện sẽ được kích hoạt và đầu ra sẽ có dòng điện chạy qua.
Đầu vào mạch điện không cần thiết phải là một công tắc, và đầu ra không nhất thiết phải là bóng đèn điện. Ta có thể nối rơ le này với một rơ le khác như sau:


Đầu ra của rơ le trên sẽ cung cấp điện cho rơ le phía dưới. Như bạn có thể thấy, cách duy nhất đó chính là đóng cả 2 công tắc cùng lúc.


2 rơ le được nối tiếp như vậy còn được biết đến là cổng AND, và được ký hiệu như sau:


Đây chính là một trong 4 cổng logic cơ bản.

$2$. Các loại cổng logic:
* Cổng **AND**:
Cổng **AND**, đúng như cái tên của nó miêu tả, hoạt động giống như logic **AND** trong ngôn ngữ lập trình. Nó sẽ trả về true khi và chỉ khi hai hoặc nhiều đầu vào đều có giá trị true. Nếu không, nó sẽ trả về giá trị false.
Dưới đây là ký hiệu minh hoạ cho cổng **AND**:
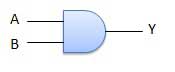
Bảng giá trị cổng **AND**:

| A | B | AB |
| --- | --- |:---:|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

* Cổng **OR**:
Là phép toán logic hoạt động dựa trên logic **OR** trong ngôn ngữ lập trình. Cổng sẽ cho đầu ra $true$ khi một trong hai hoặc input là $true$. Nếu tất cả các input đều là $false$, thì output là $false$. Dưới đây là ký hiệu cho cổng **OR**:
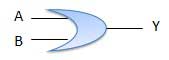
Bảng giá trị cho cổng **OR**:

| A | B | A+B |
| --- | --- |:---:|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
* Cổng **XOR**:
Cổng **XOR** (hay còn gọi là **exclusive-OR**) sẽ trả về giá trị $true$ nếu như 1 trong 2, nhưng nếu cả 2 đầu vào đều là $true$ hoặc $false$ thì output sẽ là $false$. Nói cách khác, nếu như 2 đầu vào giống nhau, output sẽ là 1 và ngược lại, nếu như 2 input khác nhau, output sẽ là 0.
Ký hiệu cho cổng **XOR**:
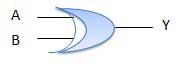
Bảng ký hiệu của cổng **XOR**:

| A | B | A (+) B |
| --- | --- |:-------:|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
* Cổng **NOT**:
Cổng NOT là một loại cổng khá đặc biệt. Nó được dùng để đảo ngược lại giá trị của đầu vào. Nếu như input là $true$, thì output là $false$. Và ngược lại, nếu input là $false$, thì output là $true$.
Ký hiệu của cổng **NOT**:
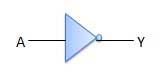
Bảng ký hiệu cổng **NOT**:

| A | B |
| - | - |
| 0 | 1 |
| 1 | 0 |
* Cổng **NAND**:
Cổng **NAND** là một sự kết hợp của 2 cổng logic **AND** và **NOT**. Như vậy, ta có thể hiểu rằng nó hoạt động giống như cổng **AND**, nhưng output sẽ bị đảo ngược lại. Cổng sẽ trả về giá trị $false$ nếu như cả 2 input đều là $true$. Nếu không, output là $true$.
Ký hiệu cổng NAND:
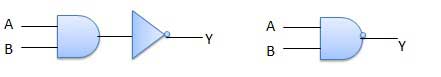
Bảng giá trị cổng **NAND**:

| A | B | AB với cái gạch trên đầu |
| --- | --- |:------------------------:|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
* Cổng **NOR**:
Giống như cổng **NAND**, cổng **NOR** là sự đảo ngược của cổng **OR**. Cổng sẽ trả về giá trị $true$ nếu như cả 2 input đều là $false$. Nếu không, output sẽ là $false$.
Ký hiệu của cổng **NOR**:
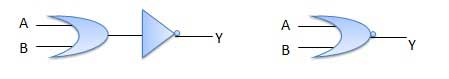
Bảng giá trị cổng **NOR**:

| A | B | A+B với cái gạch trên đầu |
| --- | --- |:-------------------------:|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
* Cổng **XNOR**:
Cổng **XNOR** là sự kết hợp của cổng **XOR** và **NOT**. Cổng sẽ trả về output $true$ nếu như cả 2 input giống nhau, và $false$ nếu như cả 2 input khác nhau.
Ký hiệu cổng **XNOR**:
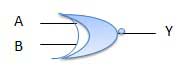
Bảng giá trị cổng **XNOR**:

| A | B | A (-) B |
| --- | --- |:-------------------------:|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

* Cổng hạt nêm **KNORR**

## 3. Adder:
$1$. Giải thích phép cộng bit:
* Thêm số nhị phân cũng giống như thêm số thập phân. Sự khác biệt lớn giữa việc thêm số thập phân và số nhị phân là bạn sử dụng một bảng đơn giản hơn nhiều cho số nhị phân:

| + | 1 | 0 |
| -------- | -------- | -------- |
| 1 | 10 | 1 |
| 0 | 1 | 0 |

* Kết quả của việc cộng một cặp số nhị phân là 2-bit, được gọi là bit tổng và bit dư (như trong "$1$ cộng $1$ bằng $0$, dư $1$"). Có thể chia bảng cộng nhị phân thành hai bảng, bảng đầu tiên cho bit tổng:

| + sum | 1 | 0 |
| -------- | -------- | -------- |
| 1 | 10 | 1 |
| 0 | 1 | 0 |

Và bảng thứ hai cho bit dư :
| + carry | 1 | 0 |
| -------- | -------- | -------- |
| 1 | 1 | 0 |
| 0 | 0 | 0 |

$2$. Giới thiệu cấu tạo cổng $XOR$:
+ Cổng $XOR$, hay còn được gọi là cổng $Exclusive OR$ vì đầu ra là $1$ khi chỉ một trong $2$ số $A$ hoặc $B$ bằng $1$. Bạn có thể sử dụng ký hiệu sau cho cổng $XOR$:
+ Bảng giá trị cổng $XOR$:

| XOR | 1 | 0 |
| -------- | -------- | -------- |
| 1 | 0 | 1 |
| 0 | 1 | 0 |

$3$. Half Adder:
+ Half Adder là một mạch logic tổ hợp với hai input và hai output. Half Adder được thiết kế để cộng hai số nhị phân bit đơn $A$ và $B$. Mạch này có hai output là số dư và tổng. Số dư là output của cổng $AND$ còn tổng là output của cổng $XOR$:

Và thay vì vẽ lại cổng AND và cổng XOR, bạn có thể chỉ cần vẽ như sau:

$4$. Full adder:
+ Full Half Adder thêm hai số một bit $A$ và $B$, và số dư $C$. Half Adder là một mạch tổ hợp ba input và hai output. Full Adder được tạo ra từ $2$ Half Adder và $1$ cổng 1 $OR$. Xem hình sau để hiểu rõ cách hoạt động của Full Adder:

Thay vì vẽ lại sơ đồ trên, Full Adder có thể vẽ như sau:
+ Bảng tóm tắt tất cả các input và output của Full Adder:
| A | B | số dư input | tổng | số dư output |
| -------- | -------- | -------- | -------- | ------ |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |

$5$. 8-bit Adder:
+ 8-bit Full Adder có thể được tạo ra từ 8 Full Adder. Số dư từ Full Adder đầu tiên là input cho Full Adder thứ hai. Các Full Adder tiếp theo được nối theo cùng một cách. Mỗi số dư output từ Full Adder là số dư input cho Full Adder tiếp theo.
Thay vì vẽ sơ đồ với 8 Full Adder, có thể vẽ 8-bit Full Adder như sau:
$A_{7}$..$A_{0}$ và $B_{7}$..$B_{0}$ biểu thị các bit của $A$ và $B$. $S_{7}$...$S_{0}$ hiển thị các bit của $S$ với $S$ là kết quả của phép cộng. Bởi vì phép cộng 2 số 8-bit có thể cho kết quả là $1$ số 9-bit nên cần số dư output biểu thị cho bit đó.
+ n-bit Adder cũng có thể tạo ra tương tự như trên.

## 4. Phép trừ:
Như ta đã biết, phép trừ và cộng liên quan mật thiết với nhau: phép trừ $A$ cho $B$ thực chất là phép cộng $A$ với số đối của $B$. Khác biệt ở chỗ, đối với phép cộng ta có "nhớ", còn đối với phép trừ thì đó là "mượn". Bây giờ, ta sẽ tìm cách thực hiện phép trừ mà không cần "mượn".

Xét ví dụ: Phép trừ $253$ cho $176$.

+ Ta thực hiện 1 vài phép biến đổi trong hệ cơ số 10:
$253 - 176 = 253 - 176 + 1000 - 1000 = 253 + (999 - 176) + 1 - 1000$
Đầu tiên ta thực hiện phép trừ $999$ (số bị trừ) cho $176$ (số trừ). Hiển nhiên phép trừ này được thực hiện đơn giản mà không cần "mượn". Phép trừ một số từ $1$ số gồm các chữ số $9$ cho kết quả được gọi là: Bù $9$ (Nine's complement). Sau đó ta lấy kết quả này cộng với $253$, rồi với $1$, sau đó trừ đi $1000$. Phép trừ cuối rõ ràng cũng không cần đến "mượn".

+ Thực hiện điều tương tự với hệ nhị phân:
Biểu diễn: $253_{10} = 11111101_2; 176_10 = 10110000_2$. Thay vì lấy $1$ số gồm các chữ số $9$ trừ đi số trừ như trước, ta lấy số gồm các chữ số $1$. Kết quả của phép trừ này cho ta $1$ số được gọi là: Bù $1$ (One's complement). Do đó, sau khi thực hiện phép trừ, mọi bit $0$ của số trừ sẽ chuyển thành $1$ và mọi bit $1$ sẽ chuyển thành $0$. Điều này dẫn ta đến một nhận xét rằng: kết quả của phép trừ chính là kết quả của phép NOT với số trừ (hay Invert của số trừ). Tiếp theo, ta cộng kết quả thu được với số bị trừ ($11111101$), cộng tiếp với $1$, và cuối cùng là trừ đi ($100000000$) để ra được kết quả của phép toán.

+ Thế với phép trừ cho kết quả âm: Ví dụ như: $176 - 253$ thì sẽ thế nào?
Ta vẫn thực hiện như trên: Tính Bù $1$ của $11111101$, ta được $00000010$, đem cộng với $10110000$ được $10110010$. Bây giờ ta cần đem số này trừ đi $11111111$ để thu được kết quả cuối cùng. Để làm được điều này, ta đơn giản chỉ cần tính phần bù của $10110010$ rồi lấy kết quả là số đối của nó là xong. Kết quả cuối cùng cho được là $-77$.

Bây giờ ta sẽ cùng tìm hiểu cơ chế thực hiện phép trừ trong máy tính!

+ Nhắc lại từ phần trước, phép cộng được thực hiện dựa trên $8$-bit Adder từ các cổng logic như sau:
Inputs từ $A0$ đến $A7$ và $B0$ đến $B7$ được kết nối với các switches biểu thị cho phép cộng hai số $8$-bit. Outputs từ $S0$ đến $S7$ được kết nối với $8$ bóng đèn để hiển thị kết quả của phép cộng. Bởi vì phép cộng 2 số $8$-bit có thể cho kết quả là một số $9$-bit nên Carry Out ouput được kết nối với bóng đèn thứ $9$.
Bảng điều khiển thể hiện phép cộng $183$ ($10110111$) và $22$ ($00010110$) cho kết quả là $205$ ($11001101$) trông như thế này:
Bảng điều khiển cho cả phép cộng và trừ hai số $8$-bit có sự thay đổi một chút bằng việc thêm vào $1$ switch để biểu thị đây là phép cộng hay trừ.
Một điểm khác biệt nữa ở đây là bóng đèn thứ $9$ được gán là: "Overflow/Underflow", có nghĩa là để biểu thị rằng phép toán cho kết quả có thể biểu diễn bằng $8$-bit (tương ứng với $9$ bóng đèn) hay không? Ví dụ như khi chúng ta thực hiện phép cộng cho ra kết quả lớn hơn $255$ hay ta thực hiện phép trừ cho ra kết quả âm, bóng đèn thứ $9$ này sẽ sáng.
Ở trên ta thấy rằng, để thực hiện phép trừ thì ta cần thực hiện phép Invert (hay $NOT$) đối với số trừ. Phép cộng thì không có điều này. Để thiết kế hai cơ chế này cùng trong một bảng điều khiển, ta có thể thiết kế mạch điện như sau:
Nhắc lại rằng:  là cổng $XOR$ với bảng giá trị là:

| $XOR$ | 0 | 1 |
| -------- | -------- | -------- |
| 0 | 0 | 1 |
| 1 | 1 | 0 |

Khi tín hiệu Invert là $0$ thì $8$ outputs của cổng $XOR$ chính là $8$ inputs. Đây là tín hiệu Invert biểu thị cho phép cộng. Ngược lại, nếu tín hiệu Invert là $1$ thì $8$ inputs sẽ đảo lại. Lúc này, tín hiệu Invert biểu thị cho phép trừ.
Lúc này, ta có một mạch điện kết hợp cả $2$ phép toán cộng và trừ như sau:
Chú ý đến $3$ tín hiệu $SUB$. Tín hiệu thứ nhất cho hộp Ones' Complement như giải thích ở bên trên. Đối với tín hiệu $SUB$ thứ $2$, nhắc lại một chút: Đối với phép trừ, sau khi ta thực hiện phép cộng số bị trừ và Invert của số trừ thì ta phải cộng thêm $1$ nên ở đây ta sẽ thực hiện bằng cách đặt giá trị $CI$ (Carry In) bằng $1$. Đối với phép cộng thì $CI = 0$. Tín hiệu $SUB$ thứ 3 được $XOR$ với $CO$ (Carry Out). Ta cùng phân tích điều này: Đối với phép cộng ($SUB = 0$), bóng đèn số 9 sẽ sáng nếu $CO$ output là $1$. Điều này có nghĩa là: Output của phép cộng lớn hơn $255$ (Overflow). Đối với phép trừ ($SUB = 1$), nếu số bị trừ lớn hơn số trừ thì $CO = 1$ (Điều này hoàn toàn hợp lí vì ta phải trừ đi cho $100000000$ ở bước cuối cùng). Bóng đèn sáng khi $CO = 0$, tức số trừ lớn hơn số bị trừ. Với việc thiết kế như trên thì máy không biểu thị được số âm, không thực hiện được phép trừ này. Tóm lại, việc thiết kế tín hiệu $SUB$ thứ $3$ như trên giúp ta hiểu rằng: Bóng đèn thứ $9$ sẽ sáng khi xảy ra overflow hay underflow đối với phép toán thực hiện.

Bây giờ ta sẽ nói về cách máy tính biểu thị số âm. Phương pháp được sử dụng phổ biến là: Bù $2$ (Two's complement). Giả sử chúng ta đang bàn về các số $8$ bits. Khoảng từ $00000000$ đến $11111111$ biểu diễn các số thập phân từ $0$ đến $255$. Tuy nhiên, nếu chúng ta muốn biểu diễn số âm, ta coi mọi số $8$-bit bắt đầu với bit có giá trị bằng $1$ đều là số âm. Khi đó ta mỗi biểu diễn nhị phân ứng với mỗi giá trị như sau: $10000000$ ($-128$), $10000001$ ($-127$), $10000010$ ($-126$), $10000011$ ($-125$), ..., $11111101$ ($-3$), $11111110$ ($-2$), $11111111$ ($-1$), ...
Ta thấy: Giới hạn các số chúng ta vừa biểu diễn bây giờ trở thành: từ $-128$ đến $127$
Để tính bù $2$ của $1$ số, đầu tiên ta tính bù $1$ của số đó và sau đó cộng thêm $1$. Điều này đồng nghĩa với việc ta Invert tất cả các chữ số rồi cộng với $1$. VD: Biểu diễn nhị phân của $125$ là $01111101$. Để biểu diễn $-125$, ta Invert $01111101$ để được $10000010$, sau đó cộng 1 để được $10000011$.
Như vậy, ta đã có $2$ cách để biểu diễn các số nhị phân, đó là có dấu (signed) và không dấu (unsigned). Các số unsigned $8$-bit trong khoảng từ $0$ đến $255$ và các số signed $8$-bit trong khoảng từ $-128$ đến $127$.

## 5. Các dạng mạch logic khác:

Dưới đây là 4 dạng mạch tổ hợp đơn giản mà chúng ta nên biết qua trước khi tiến sâu hơn vào các dạng mạch phức tạp hơn như RAM, CPU, v.v.

1. Multiplexer (Mạch ghép kênh):

Multiplexer, viết tắt là **MUX** hoặc **MPX**, là một dạng mạch tổ hợp đặc biệt được sử dụng để lựa chọn một trong $n$ dữ liệu đầu vào (input) và dẫn nó tới đầu ra. Giá trị đầu ra sẽ được quyết định thông qua một bộ giá trị chọn lựa (selected input) gồm $m$ đầu vào mà trong đó, $2 ^ m = n$.

Hình ảnh phía dưới là biểu diễn cơ học của một Multiplexer:

<center>
<img src="https://i.imgur.com/rwyGLHh.png">
</center>

Sử dụng công tắc xoay như trong hình, chúng ta có thể lựa chọn các giá trị đầu ra, tạo thành Multiplexer cơ học. Trong kĩ thuật điện tử, các Multiplexer được thiết kế nhỏ gọn trong một mạch IC (integrated circuit) thay vì sử dụng mạch cơ học như phía trên.

Cấu tạo của Multiplexer cơ học trên sử dụng một công tắc xoay cơ học, và khiến cho cấu trúc của nó trở nên rất cồng kềnh và phức tạp. Để đơn giản hóa và biến nó trở thành một mạch logic thực thụ, người ta sử dụng phương pháp triệt tiêu số lượng cổng logic. Chính vì vậy, bộ giá trị chọn lựa được sử dụng như một công cụ nhằm thay thế cho công tắc xoay, khi nó có thể thay thế việc lựa chọn giá trị thứ $k$ trong $n$ giá trị đầu vào bằng cách biểu diễn trên $2^m$ đầu vào.

Để dễ hình dung, chúng ta sẽ sử dụng Multiplexer 4:1, với số đầu vào biểu diễn giá trị chọn lựa là $m = 2$ và số giá trị đầu vào là $n = 2^m = 4$:

<center>
<img src="https://i.imgur.com/86hqrli.png">
</center>

Với mạch logic trên, chúng ta có thể biểu diễn nó dưới dạng Boolean qua công thức sau:
$Q = \overline{ab}A + a\overline{b}B + \overline{a}bC + abD$

Sử dụng công thức này, chúng ta có được bảng giá trị thực dưới đây:

|b|a|D|C|B|A| Q |
|-|-|-|-|-|-|:-:|
|0|0|x|x|x|1| 1 |
|0|1|x|x|1|x| 1 |
|1|0|x|1|x|x| 1 |
|1|1|1|x|x|x| 1 |

Multiplexer được sử dụng chủ yếu để tăng lượng dữ liệu có thể được gửi qua mạng trong phạm vi thời gian và băng thông nhất định, ví dụ thay vì truyền $2^n$ kênh thì chỉ cần 1 đường truyền dữ liệu và $n$ đường địa chỉ. Tức là Multiplexer làm cho nhiều tín hiệu có thể chia sẻ một thiết bị hoặc tài nguyên, ví dụ mạch chuyển đổi ADC hoặc một thiết bị xử lý thông tin, thay vì bố trí mỗi thiết bị cho mỗi tín hiệu đầu vào.

2. Demultiplexer (Mạch giải ghép kênh):

Demultiplexer, viết tắt là **Demux**, là một dạng mạch tổ hợp với cấu trúc cũng như công dụng ngược hoàn toàn so với Multiplexer mà chúng ta đã đề cập ở phần trước đó. Demultiplexer tiếp nhận duy nhất 1 dữ liệu đầu vào $F$ và sẽ sử dụng bộ giá trị chọn lựa tương tự gồm $m$ đầu vào như ở Multiplexer để điều hướng $F$ tới $n$ đầu ra khác nhau ($n = 2^m$).

Ví dụ, với Demultiplexer 1:4, chúng ta có thể biểu diễn nó dưới dạng cổng logic như sau:

<center>
<img src="https://i.imgur.com/13NMC4b.png">
</center>

Với mạch logic trên, ta tiếp tục biểu diễn nó dưới dạng Boolean qua công thức sau:
$F = \overline{ab}A + a\overline{b}B + \overline{a}bC + abD$

Với công thức trên, chúng ta có thể biểu diễn nó bằng bảng giá trị thực như sau:

|F|b|a|D|C|B|A|
|-|-|-|-|-|-|-|
|1|0|0|0|0|0|1|
|1|0|1|0|0|1|0|
|1|1|0|0|1|0|0|
|1|1|1|1|0|0|0|

3. Encoder (Mạch mã hóa):

Khác với Multiplexer chỉ tiếp nhận và trả về một dữ liệu duy nhất bằng cách sử dụng bộ giá trị chọn lựa, Encoder (còn đuọc biết tới là Binary Encoder) lấy TOÀN BỘ các dữ liệu đầu vào tại cùng một thời điểm và chuyển đổi chúng thành dữ liệu đầu ra. Thông thường, các Encoder có thể xuất ra các đầu ra với 2 bit, 3 bit hoặc 4 bit, phụ thuộc vào lượng dữ liệu đầu vào. Một encoder $n$ bit sẽ có $2^n$ đầu vào và n bit đầu ra, từ đó tạo ra các bộ encoder như 4:2, 8:3 và 16:4.

Lấy ví dụ như Encoder 4:2, chúng ta sẽ có mạch logic như sau:

<center>
<img src="https://i.imgur.com/vghmoNR.png">
</center>

Chúng ta sẽ có biểu diễn Boolean theo công thức sau:
$A_1 = Y_3 + Y_2$
$A_0 = Y_3 + Y_1$

|Y3|Y2|Y1|Y0|A1|A0|
|--|--|--|--|--|--|
|0 |0 |0 |1 |0 |0 |
|0 |0 |1 |0 |0 |1 |
|0 |1 |0 |0 |1 |0 |
|1 |0 |0 |0 |1 |1 |

Bên cạnh Encoder cơ bản, chúng ta còn có một dạng khác gọi là Priority Encoder, hay "Mạch mã hóa ưu tiên". Như tên gọi của nó, các đầu vào sẽ có độ ưu tiên tăng dần, và kết quả đầu ra sẽ được lấy theo đầu vào ở trạng thái bật (1 bit) có độ ưu tiên cao nhất, đồng thời bỏ qua tất cả các đầu vào còn lại với độ ưu tiên thấp hơn hoặc ở trạng thái tắt (0 bit).

Lấy ví dụ trên chip TTL 74LS148 là một dạng Priority Encoder 8-to-3-bit, chúng ta có thiết kế đơn giản như sau:

<center>
<img src="https://i.imgur.com/6DiRxER.png">
</center>

Lấy ví dụ, chúng ta có các đầu vào $D_2 = D_3 = D_5 = 1$ và các đầu vào còn lại đều mang giá trị 0. Vì $D_5$ có độ ưu tiên cao nhất nên đầu ra sẽ lấy giá trị của nó, tương đương với $Q_2 = 1, Q_1 = 0, Q_0 = 1$. Giá trị của $D_5$ sẽ bị bỏ qua khi và chỉ khi có một đầu vào với độ ưu tiên cao hơn chuyển sang giá trị 1.

Từ nhận xét trên, chúng ta sẽ đưa ra được bảng giá trị thực sau đây:

|D7|D6|D5|D4|D3|D2|D1|D0|Q2|Q1|Q0|
|--|--|--|--|--|--|--|--|--|--|--|
|0 |0 |0 |0 |0 |0 |0 |1 |0 |0 |0 |
|0 |0 |0 |0 |0 |0 |1 |X |0 |0 |1 |
|0 |0 |0 |0 |0 |1 |X |X |0 |1 |0 |
|0 |0 |0 |0 |1 |X |X |X |0 |1 |1 |
|0 |0 |0 |1 |X |X |X |X |1 |0 |0 |
|0 |0 |1 |X |X |X |X |X |1 |0 |1 |
|0 |1 |X |X |X |X |X |X |1 |1 |0 |
|1 |X |X |X |X |X |X |X |1 |1 |1 |

Với $X$ là các giá trị bị bỏ qua do độ ưu tiên thấp.

Từ đó, chúng ta rút ra được công thức tổng quát của từng đầu ra:
$Q_0 = \Sigma{(\overline{D_6}(\overline{D_4}\overline{D_2}D_1 + \overline{D_4}D_3 + D_5) + D_7)}$
$Q_1 = \Sigma{(\overline{D_5}\overline{D_4}(D_2 + D_3) + D_6 + D_7)}$
$Q_2 = \Sigma{(D_4 + D_5 + D_6 + D_7)}$

Priority Encoder có thể được sử dụng nhằm giảm số lượng dây nối cần tới trong một mạch nhất định với nhiều đầu vào khác nhau. Ví dụ, một máy tính cần đọc dữ liệ từ 104 phím khác nhau trong bàn phím chuẩn QWERTY với mỗi phím chỉ cần nhấn xuống 1 lần, tương đương với các bit 1 và 0. Thai vì sử dụng đủ 104 dây để kết nối từng phím với máy tính, người ta ánh xạ từng kí tự về dạng mã ASCII của nó, và chỉ tốn đúng 7 bit (từ 0 tới 127) cần tới ở đầu ra.

4. Decoder (Mạch giải mã):

Tương tự với Demultiplexer là đảo ngược của Multiplexer, Decoder là dạng đối nghịch của Encoder và được sử dụng với mục đích giải mã. Nếu Encoder là mã hóa các đầu vào và trả về dạng bit của nó, như $5 \rightarrow 101$, thì Decoder sẽ có nhiệm vụ giải mã các bit được đưa vào và trả về giá trị thập phân của nó, như $101 \rightarrow 5$.

Decoder có nhiều loại đầu vào như 2-bit, 3-bit hay 4-bit, phụ thuộc vào số dòng đầu vào. Với n-bit đầu vào thì sẽ có thể hiển thị $2^n$ giá trị đầu ra.

Chúng ta đã quen thuộc với dạng 2-to-4 Decoder được dùng để trả về một giá trị có 2 bit, như $11 \rightarrow 3$. Tuy vậy, không phải lúc nào cũng cần tới một mạch Decoder đặc thù cho việc giải mã một lượng bit nhất định. Ví dụ, để thực hiện giải mã 4 bit ra 16 giá trị khác nhau, chúng ta hoàn toàn có thể dùng 2 mạch 3-to-8 Decoder như sau:

<center>
<img src="https://i.imgur.com/IPPJZFT.png">
</center>