---
title: Bubble Sort in Java - Scaler Topics
description: This article explains the algorithm & provides the code of Bubble Sort in Java. It takes you through an optimized bubble sort algorithm & analyses the time & space complexities.
author: Himanshu Yadav
category: Java
---

:::section{.abstract}

Bubble sort in [Java](https://www.scaler.com/topics/course/java-beginners/) is the simplest, comparison-based sorting algorithm which helps us sort an array by traversing it repeatedly, comparing adjacent elements, and swapping them based upon desired sorting criteria. Bubble sort is an `in-place` algorithm, meaning it does not require extra space; it changes the original array instead.

For more understanding, you may read more about [Bubble Sort Algorithm](https://www.scaler.com/topics/data-structures/bubble-sort/).

:::
:::section{.main}

## Algorithm for Bubble Sort in Java

Using the bubble sort algorithm, we can sort an unsorted array `A` of size `N` in increasing order in three simple steps. Traverse the array `N-1` times and follow the steps.

1. Starting with the very first element of the array, compare the current element with the **next consecutive** element.
2. If the current element `A[i]` is greater than the next element `A[i+1]`, swap them, move to the next element, and repeat `step 2`.
3. Otherwise, move to the next element and repeat `step 2`.

:::

:::section{.main}

## Bubble Sort Example

Let's take an unsorted array `A = [7,11,9,2,4]` containing five elements. We will sort it in increasing order using the Bubble sort in Java. Our desired output is ` [2,4,7,9,11] `.

To sort the array, we need a total of `4 (N-1)` passes indexed from `0` to `3`.

Let's walk through the algorithm step by step.

### First pass (PassNum = 0)
* **index = 0**, we compare `A[0] and A[1]` since `7 < 11`, so there is no change in the array, and we move to the next element.
* 

* **index = 1**, `A[1]` which is `11` is greater than `A[2]` which is `9` so we swap `A[1] and A[2]`, the array becomes `[7,9,11,2,4]` and we move to the next element.
* 

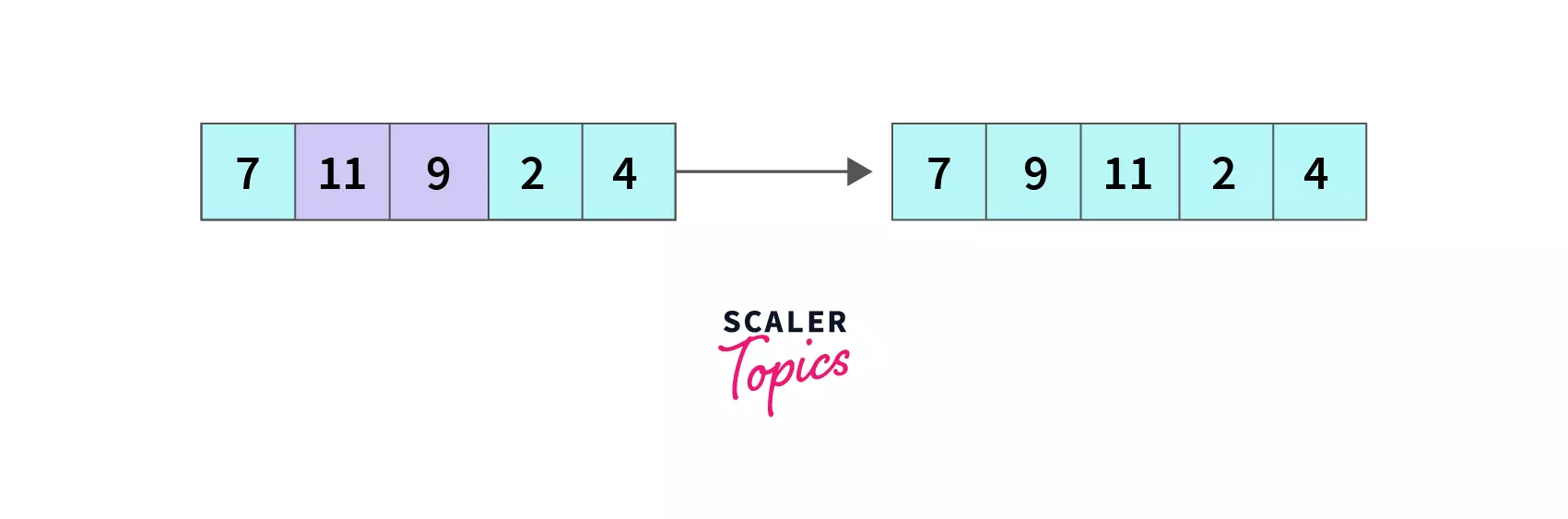
* **index = 2**, compare `A[2]` with `A[3]`, `11 > 2` so `A[2] and A[3]` are swapped and the array becomes `[7,9,2,11,4]` and we move to next element.
* 

* **index = 3**, compare `A[3]` with `A[4]`, `11 > 4` so `A[3] and A[4]` switch their places resulting the array as `[7,9,2,4,11]`.
* 

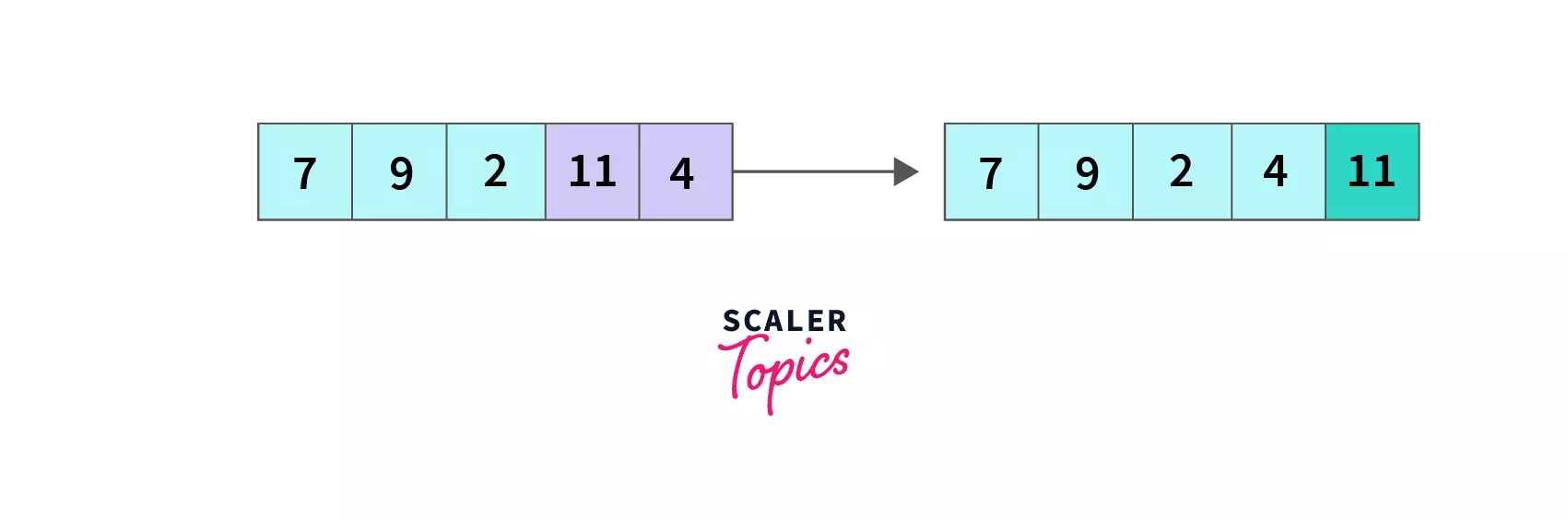
End of the first pass, we compared all five elements in pairs by iterating till the second last element, and as a result, `11` is pushed to its desired position, and the array is `[7,9,2,4,11]` now.

### Second pass (PassNum = 1)
* **index = 0**, we compare `A[0] and A[1]`, since `7 < 9`, so there is no change in the array, we move to the next element.
* 

* **index = 1**, `A[1]` is `9` is greater than `A[2]` is `2` so we swap `A[1] and A[2]`, the array becomes `[7,2,9,4,11]` and we move to the next element.
* 

* **index = 2**, compare `A[2]` with `A[3]`, `9 > 4` so `A[2] and A[3]` are swapped and the array becomes `[7,2,4,9,11]`.
* 

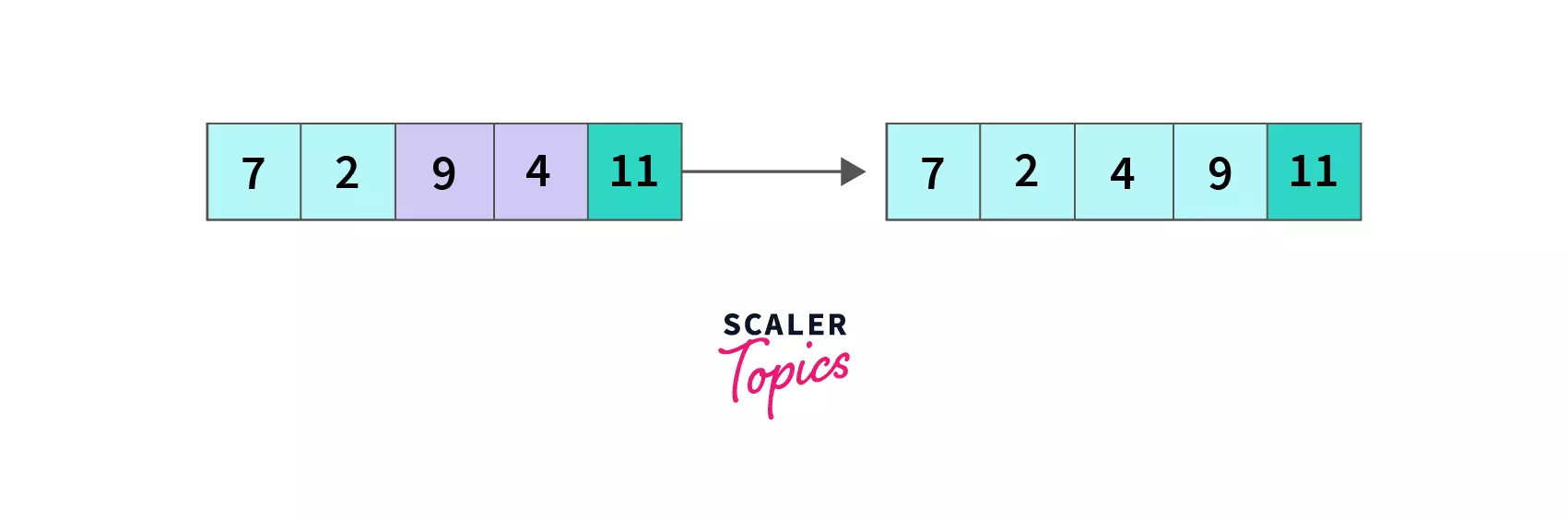
At the end of the second pass, we compared all four remaining unsorted elements (11 were sorted in the first pass) in pairs by iterating until the second last element. As a result, `9` (the largest of the remaining 4 elements) is pushed to its desired position, and the array is `[7,2,4,9,11]` now.

### Third pass (PassNum = 2)
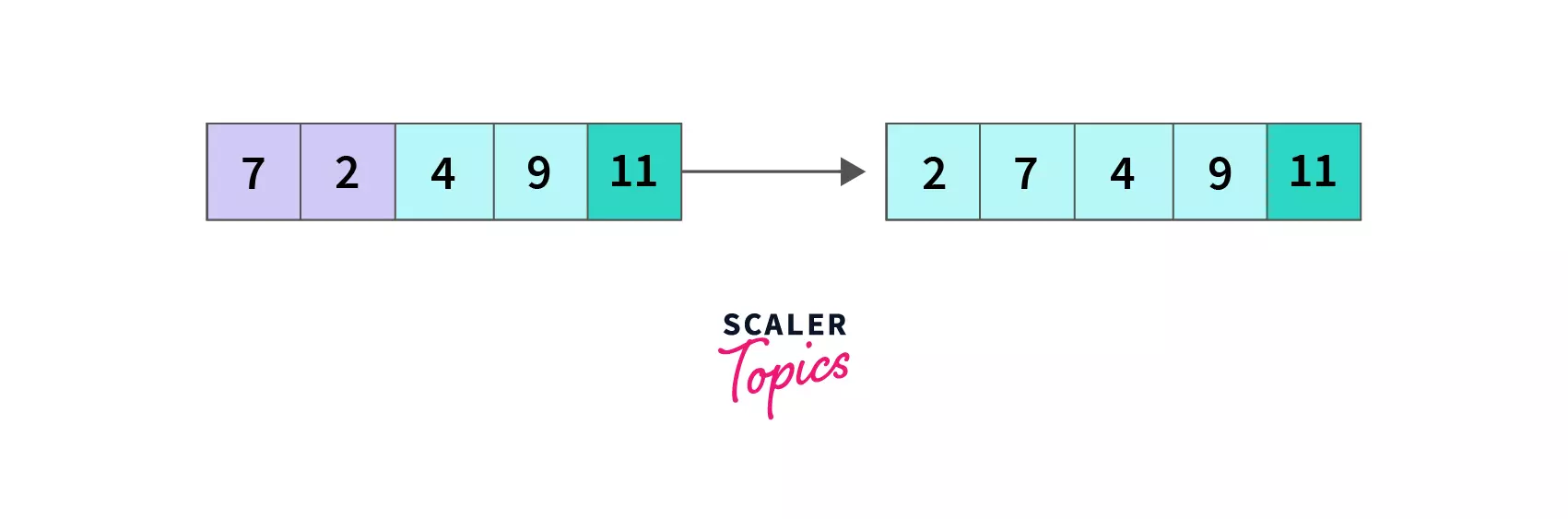
* **index = 0**, `A[0]` which is 7 is greater than `A[1]` that is 2 so we swap `A[0] and A[1]`, the array becomes `[2,7,4,9,11]` and we move to the next element.
* 

* **index = 1**, compare `A[1]` with `A[2]`, `7 > 4` so `A[2] and A[3]` are swapped and the array becomes `[2,4,7,9,11]`.
* 

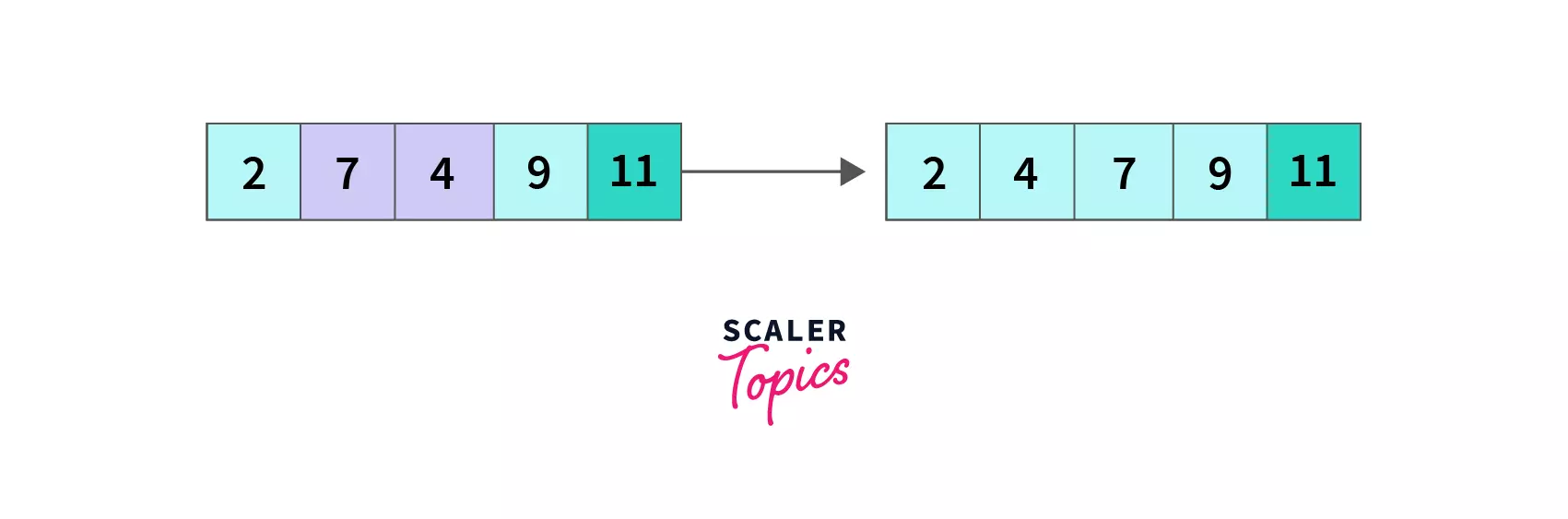
At the end of the third pass, we have compared all three remaining unsorted elements (`9` and `11` were sorted earlier) in pairs by iterating until the second last element. As a result, `7` (the largest of the remaining three elements) is pushed to its desired position, and the array is `[2,4,7,9,11]` now.

### Fourth pass (PassNum = 3)
* **index = 0**, we compare `A[0] and A[1]`, since `2 < 4`, so no change in the array.
* 

At the end of the fourth pass, even though the array was sorted in the third pass, we don't have a way to check if it's sorted and end the loop. As a result, we had to complete the maximum number of N-1 passes possible.

:::

:::section{.main}

## Implementation of Bubble Sort in Java

The below Java program is the implementation of a bubble given unsorted array A of length N.

public static void bubble sort(int[] A, int N)
{
    for (int PassNum = 0; PassNum < N - 1; PassNum++) // for N-1 passes
    { 

        for (int index = 0; index < N - PassNum - 1; index++) // to iterate through the comparision loop
        { 

            if (A[index] > A[index + 1]) // current number is greater then next element then swap
            { 

                int swap = A[index];
                A[index] = A[index + 1];
                A[index + 1] = swap;
            }
        }
    }
}

### Complexity Analysis

**Time complexity:**
* **Worst Case:** O($N^2$)
* **Best Case:** O(N)

**Space Complexity:**
* O(1)

:::

:::section{.main}

## Advantage of Bubble Sort in Java

- The bubble sort's main advantage is that it is widely used and simple to implement.
- In its best-case scenario, which checks whether the array is already sorted, the **optimized algorithm** is highly efficient.
- Bubble sort is an in-place sorting technique, which means it does not require additional space to sort the array; it can **modify the original array**.

:::

:::section{.summary}

## Conclusion

* Bubble sort is a sorting alogrithm used to sort an array.
* Its time complexity is O(N2).
* Bubble sort is a in-place sorting algorithm.

:::