## Topics & Questions covered
1. **Prefix sum**
a) Range Sum queries
b) Equilibrium index
2. **Carry forward**
a) count ```ag``` Pairs
b) Leaders in an array
3. **Subarrays**
a) Contribution Technique
b) Sliding window

## Problem : Range Sum Queries

### Question
Given an array arr[] of n elements and q queries. For each query, given indices l and r, calculate and print sum of all elements in range [l,r]. (l and r included)

**Note:** l and r are array indices.

### Constraints:
1 <= n, q <= 10^5
1 <= arr[i] <= 10^9
0 <= l <=r < n

### Example:
arr[10] = [-3, 6, 2, 4, 5, 2, 8, -9, 3, 1]
No. of queries = 6
Two arrays l[6] and r[6] are provided in the input, as follows:

l[6] = [4, 3, 1, 7, 3, 0]
r[6] = [8, 7, 3, 7, 6, 4]

**Answer:**
We mark the indices of the array for clarity:
|index | 0 | 1| 2|3|4|5|6|7|8|9|
|----|----|----|-----|----|----|----|---|----|-----|---|
|arr|-3|6|2|4|5|2|8|-9|3|1|

The sums will be:
|Query| l | r | sum |
|----| -------- | -------- | ----|
|0| 4 | 8 | 9
|1|3|7|10|
|2|1|3|12|
|3|7|7|-9|
|4|3|6|19|
|5|0|4|14|

### Brute Force Idea
* For every query, iterate and sum the elements from index l to r.
* So, iterate over the queries and perform the above operation for each query.
* Try coding the brute force solution.
* The time complexity of brute force solution is O(q*n) which might lead to TLE, hence we need an optimized solution.

### How to Optimize?
1. We will create prefix sum array. In general, **psum[i] = psum[i-1] + arr[i]**

    long psum[n];
    psum[0] = arr[0];
    for (int i = 1; i < n; i++)
    {
        psum[i] = psum[i - 1] + arr[i]
    }

2. Now the answer of sum(L to R) will be

   If(L == 0) 
       sum = psum[R] 
   else 
       sum = psum[R] - psum[L-1]

### Complete code for Range sum queries

## Solution for Range sum queries 
So, the idea is:
1. Create the prefix sum array from the given array
2. Find the sum of elements in constant time by the formula observed

void solve(int l[], int r[], int n, int arr[])
{
    long psum[n];
    psum[0] = arr[0];
    for (int i = 1; i < n; i++)
    {
        psum[i] = psum[i - 1] + arr[i]
    }

    for (int i = 0; i < q; i++)
    {
        //this is ith query (l[i] and r[i])
        int start = l[i], end = r[i];
        if (start == 0)
        {
            print(psum[end]);
        }
        else
        {
            print(psum[end] - psum[start - 1]);
        }
    }
}

**Time Complexity:**
**TC: O(n+q)**

**Space Complexity:**
**SC: O(n)**

## Problem : Equilibrium Index

### **Question:**
Given an array arr[] of n elements, count the number of equilibrium indices.**

An index i is said to be equilibrium index if sum of all indices on left of `i`th index is equal to the sum of all indices on right of `i`th index.

**Note:**
If i== 0, left sum = 0;
If i==n-1, right sum = 0;

### **Constraints:**
1 <= n <= 
1 <= arr[i] <= 

### **Example:**
arr[4] = [-3, 2, 4, -1]

We find leftsum and rightsum for each index:
| index | 0 | 1 | 2 | 3 |
| -------- | --- | --- | --- | --- |
| arr | -3 | 2 | 4 | -1 |
| leftsum | 0 | -3 | -1 | 3 |
| rightsum | 5 | 3 | -1 | 0 |

* So, in above example, the leftsum and rightsum are same at index 2, where both are -1.
* Index 2 is the only equilibrium index present. So, answer = 1

### **Observation:**
* For every element, we are calculating the sum from index 0 to the element previous to it, and similarly from next to last element.

<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/052/138/original/Screenshot_2023-10-03_at_8.29.57_PM.png?1696345223" alt= “” width ="500" height="100">

* This is similar to the range sum we were calculating in the last question.
* So, this question can be solved with the help of prefix sum.

### **Solution:**
So, the solution will be:
* Create the prefix sum array. Then, to calculate the sum of elements from l to r (both included):

if l==0: 
    psum[r]
else: 
    psum[r] - psum[l-1]

* So, to calculate leftsum for index i, which is sum from 0 to i-1:
= **psum[i-1]** (as in this case start index is 0)
* To calculate rightsum for index, i, which is sum from i+1 to last index:
= **psum[n-1] - psum[i]**
* Remember to handle the edge case, when i== 0, otherwise the code will produce error.

### **Code:**

int equilibrium(int arr[], int n){
    long psum[n];
    psum[0] = arr[0];
    for (int i = 1; i < n; i++){
        psum[i] = psum[i - 1] + arr[i]
    }

    int cnt = 0;
    for (int i = 0; i < n; i++){
        long left;
        if (i == 0)
            left = 0;
        else
            left = psum[i - 1];

        long right = psum[n - 1] - psum[i];
        if (left == right)
            cnt++;
    }

    return cnt;
}

**Time Complexity:**
**O(n+n)** **O(n)**

**Space Complexity:**
**O(n)**

## DSA : Carry Forward

## Problem : Count Pairs 'ag'
Given a character array ch[N] of size N, We have to calculate the number of pairs of indices i, j where i<j && ch[i] == 'a' && ch[j] == 'g'

## Constraints

- 1 <= N <= 10^5
- 'a' <= ch[i] <= 'z'

## Example

**Input:** ch[8] = {b, a, a, g, d, c, a, g}
**Output:** 5

### Example Explanation:
Let us write an index of every element of an array

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| --- | --- | --- | --- | --- | --- | --- | --- |
| b | a | a | g | d | c | a | g |

**Pairs(i, j) where ch[i]='a' and ch[j]='g' and i<j are:**

(1,3), (2,3), (1,7), (2,7), (6,7)

So there are total 5 pairs.

## Idea 1

Generate all pairs such that `i<j` and count if `ch[i]=='a' && ch[j]=='g'`
We can generate all the pairs by using the nested loop.

## PsuedoCode

int pairs(char ch[]){
    int N = ch.length, c=0;
    for(int i = 0; i < N ; i++){
        for(int j = i+1 ; j < N ; j++){
            if( ch[i]=='a' && ch[j]=='g' )
                c=c+1;
        }
    }
    return c;
}

## Time and Space Complexity
Time Complexity: **O(N^2)**
Space Complexity: **O(1)**

## Idea 2 : Optimised idea

1. Set cg=0 and ans=0
1. Iterate from right to left in a string and keep the count of the number of g's in `cg` variable.

|0|1|2|3|4|5|6|7|8|
|-|-|-|-|-|-|-|-|-|
|a|d|g|a|g|a|g|f|g|
|||||||||cg=cg+1, cg=1|
||||||||-||
|||||||cg=cg+1, cg=2|||
||||||ans=ans+cg, ans=2|||
|||||cg=cg+1, cg=3|||
||||ans=ans+cg, ans=5|||
|||cg=cg+1, cg=4|||||
||-||||||||
|ans=ans+cg, **ans=9**||||

## Solution
1. Initialize two variables cg=0, ans=0
2. Iterate over the string from right to left
3. At every index,
a) If the character is g, then increment cg by 1
b) else if the character is a, then add cg to ans (as current can make pair with all the g's at its right)
4. Return ans.

## PsuedoCode

int pairs(char ch[]){
    int N = ch.length, cg = 0, ans = 0;
    for(int i = N-1 ; i>=0 ; i--){
        if(ch[i]=='g'){
            cg++;
        }
        else if(ch[i]=='a'){
            ans=ans+cg;
        }
    }
    return ans;
}

### Time and Space Complexity
Time Complexity: **O(N)**
Space Complexity: **O(1)**

## Problem : Leaders in Array
Given an array ar[N], you have to find a number of leaders in the array.

**Leader:** An element ar[i] is said to be a leader if it is greater than the maximum element of all elements present on the left of it i.e [0,i-1]

**Note:**
ar[0] is already considered a leader.

### Constraints
- `1 <= N <= 10^5`
- `1 <= ar[i] <= 10^9`

### Example
**Input:** ar[8] = {3, 2, 4, 5, 2, 7, -1, 15}
**Output:** 5

**Example Explanation:**

|Index| 0 | 1 | 2 |3|4|5|6|7|
| -------- | -------- | -------- |-|-|-|-|-|-|
| **Elements**|3|2|4|5|2|7|-1|15|
|**Maximum of elements present at left of current element**|-|3|3|4|5|5|7|7|
|**Leader**| yes|x|yes|yes|x|yes|x|yes|

### Brute force idea

1. For every element of an array, iterate on the left of the element to find the maximum element available at the left, and check if the current element is a leader by comparing it.
3. Try to code it up.

### Time and Space Complexity
Time Complexity: O(N^2)
Space Complexity: O(1)

### Tracing
For every element, we are iterating on all the elements left of it.

**Example:** ar[6]= 4 2 3 9 7 10

|Index| 0 | 1 | 2 |3|4|5|
| -------- | -------- | -------- |-|-|-|-|
| **Elements**|4|2|3|9|7|10|
||**leader**|||||||
||->|max on left side=4, ~~leader~~||||
||->|->|max on left side=4, ~~leader~~|
||->|->|->|max on left side=4, **leader**||||
||->|->|->|->|max on left side=9, ~~leader~~||||
||->|->|->|->|->|max on left side=9, **leader**||||

### Optimised idea

We can see in the above example, the same part of an array is iterating again and again. So instead of iterating again and again, we store the maximum value in a variable.

Let us take two variables one to store leader count i.e. `l=1` and the second is to store maximum value at the left `max=ar[0]`.
|Index| 0 | 1 | 2 |3|4|5|
| -------- | -------- | -------- |-|-|-|-|
| **Elements**|4|2|3|9|7|10|
|| l=1|2<max, l=1|3<max, l=1|9>max, l=l+1=2|7<max, l=2|10>max, l=l+1=3|
||max=4|max=4|max=4|max=9|max=7|max=10|

### Pseudocode

int leaders(int ar[]){
    int N=ar.length;
    int M=ar[0], l=1;
    for(int i=1;i<N;i++){
        // check is ar[i] leader?
        if(ar[i]>M){
            l=l+1;
            M=ar[i];
        }
    }
    return l;
}

### Time and Space Complexity
Time Complexity: **O(N)**
Space Complexity: **O(1)**

## Subarray

### Definition

A subarray is a contiguous part of an array, defined by a starting index and an ending index. It represents a subset of elements within the array.

**Note:**
* Single element is also considered as subarray.
* Complete array is also considered as subarray.
* Subarray is considered from left to right.

### Example

Consider the following array:

| 4 | 1 | 2 | 3 | -1 | 6 | 9 | 8 | 12 |
| - | - | - | - | - | - | - | - | - |

Check if below are subarrays:

| Array | True/False |
| --------------------------- | ---------- |
| 2, 3, -1, 6 | True |
| 4, 2 | False |
| 1, 2, 6 | False |
| -1, 6, 9 | True |
| 8 | True |
| 8, 9, 6 | False |
| 4, 1, 2, 3, -1, 6, 9, 8, 12 | True |
| 2, 3, 6 | False |

## Print subarray from s to e

### Problem Statement
Given an array and the starting and ending indices, print the entire subarray.

### Solution

To solve the problem of printing all subarray, we can follow these steps:

* The code directly iterates through the subarray elements using a `for` loop.
* It starts from the starting index `(start)` and continues until the ending index `(end)`.
* During each iteration, it prints the element at the current index.

**Pesudocode**

void printSubarray(int[] arr, int start, int end) {
    for (int i = start; i <= end; i++) {
        System.out.print(arr[i] + " ");
    }
    System.out.println();
}

### Time and Space Complexity
What will be T.C and S.C for the above approach?
* TC - **O(N)**
* SC - **O(1)**

## Problem : Print all subarrays
Given an array, you need to print all possible subarrays, where each subarray is printed on a new line.

<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/045/532/original/upload_df4415b4d504a2b45ad8cddff0b99c5a.png?1693570170" alt= “” width ="300" height="500">

### Idea
To print all subarrays involves generating all possible subarrays by considering each possible starting and ending index combination. For each combination, the subarray is printed on a new line.

**Code**

void printSubarrays(int[] arr) {
    int n = arr.size();

    // start of subarray
    for (int start = 0; start < n; ++start) {

        // end of subarray
        for (int end = start; end < n; ++end) {

            // printing single subarray
            for (int i = start; i <= end; ++i) {
                System.out.print(arr[i] + " ");
            }
            System.out.println();
        }
    }
}

#### Time and Space Complexity
What will be T.C and S.C for the above approach?
* TC - **O(N^3)**
* SC - **O(1)**

## Problem : Print all subarrays sum
Given an array of N elements, you need to print the sum of each subarray, where each subarray sum is printed on a new line.

### Hint
To print subarray sums involves generating all possible subarrays and calculating their sums. For each subarray, the sum is printed on a new line.

**Code**

void printSubarraySums(int[] arr) {
    int n = arr.length;

    for (int s = 0; s < n; s++) {
        for (int e = s; e < n; e++) {
            int sum = 0;
            for (int i = s; i <= e; i++) {
                sum += arr[i];
            }
            System.out.println(sum);
        }
    }
}

#### Time and Space Complexity
What will be T.C and S.C for the above approach?
* TC - **O(N^3)**
* SC - **O(1)**

### Optimized Solution
We can optimize the solution using the **Prefix Sum** technique. Try to code it up.

What will be T.C and S.C for the above approach?
* TC - **O(N^2)**
* SC - **O(N)**

### Solving without using prefix sum technique
Look at subarrays starting from 3 to get insight.

<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/045/533/original/upload_45f85c194795c4397eb0abac4a7f4758.png?1693570191" alt= “” width ="600" height="400">

From the above diagram we can observe that when we start from a particular start point we can initialise sum=0, and then run a loop for end points and keep on adding arr[e] to sum to get the subarray sum from s to e.

**Pseudocode**

void printSubarraySums(int[] arr) {
    int n = arr.length;
    for (int s = 0; s < n; s++) {
        int sum = 0;
        for (int e = s; e < n; e++) {
            sum = sum + arr[e];
            System.out.println(sum);
        }
    }
}

#### Time and Space Complexity
What will be T.C and S.C for the above approach?
* TC - **O(N^2)**
* SC - **O(1)**

## Problem : Maximum subarray sum

### Problem Statement
Given an array of n elements, return the maximum subarray sum

### Constraints
1 <= N <= 10^5
-10^6 <= arr[i] <= 10^6

### Example 1:
Arr[7] = [3, 2, -6, 8, 2, -9, 4]
Here,
max subarray = [8, 2]
maximum sum = 10

### Optimized Approach

<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/045/534/original/upload_822fa3a658ec55d1e3d4afe72eafee80.png?1693570211" alt= “” width ="600" height="400">

<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/045/535/original/upload_a1ca1babcb6f91f49e7b96fc7750c434.png?1693570235" alt= “” width ="700" height="500">

**Idea:**
If the obtained sum is positive, carry forward onto the next step/element in the said array
#### Tracing

|Index| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| **Arr** | 5 | 6 | 7 |-3 | 2 | -10 |-12 | 8 |12 |
| **S** | 5 |11 |18 | 15 |17 |7 |-5(0)| 8 |20 |
| **Ans** | 5 | 11 |18 |18 | 18 |18 |18 |18 | 20 |

So, here maximum subarray sum comes out to be 20 and the respective subrarray is from index 7-8 i.e, [8, 12]

Now, if an array has multiple negative elements our sum would often revert to 0. In such cases, it's beneficial to initialize sum and ans with the first value of the array be it negative or positive

#### Pseudocode:

long Subsum(int arr[], int n) {
    long sum = arr[0];
    long ans = arr[0];
    
    for (int i = 0; i < n; i++) {
        if (sum < 0) {
            sum = 0;
        }
        
        sum += arr[i]; 
        
        if (ans < sum) {
            ans = sum;
        }
    }
    
    return ans;
}

**Time and space complexity:**
TC: O(N)
SC: O(1)

The optimized method that we just discussed comes under **Kadane's Algorithm** for solving maximum subarray problem

### Observations related to Subarrays problems
Following are the observations that can be useful when solving problems related to subarrays:

* Subarrays are contiguous subsets of an array, and solving problems related to subarrays often involves considering different combinations and properties of these subsets.

* Iterating through all possible subarrays is a common approach to solving subarray problems, although it can result in a high time complexity.

* Utilizing prefix sums can be an effective technique to optimize subarray-related problems by reducing the time complexity.

* Keeping track of cumulative sums or using prefix sum arrays can aid in efficiently calculating subarray sums or performing subarray-related operations.

* Considering properties such as the length, sum, or even/odd nature of subarrays can help identify specific patterns or conditions to be met.

* It is crucial to understand the problem constraints and requirements, as they may provide hints for selecting appropriate algorithms or optimizing the solution.

* Exploring additional data structures or algorithms, such as segment trees or Kadane's algorithm, can further enhance the efficiency of subarray-related problem solutions.

## DSA: Contribution Technique and Sliding Window

## Problem : Sum of All the Subarray Sums

### Problem Statement
Given an array of size N return the sum of all the subarray sums.
### Example1:

Let's take the array, **{3, 4, 2}**.

All possible subarrays:
{3}, {3,4}, {3, 4, 2}, {4}, {4, 2}, {2}

| Starting Index | Ending Index | Subarray | Sum |
|:--------------:|:------------:|:---------:|:--------:|
| 0 | 0 | {3} | 3 |
| 0 | 1 | {3,4} | 7 |
| 0 | 2 | {3, 4, 2} | 9 |
| 1 | 1 | {4} | 4 |
| 1 | 2 | {4, 2} | 6 |
| 2 | 2 | {2} | 2 |
| | | | Sum = 31 |

### Pesudocode

long SubarraysSum(int[] arr) {
    long total = 0;
    int n = ar.length;
    for(int s = 0; e < n; s++){
       long sum = 0;
       for(int e = s; e < n; e++){
            sum = sum + ar[e];
            //subarray sum [s..e]
            total = total + sum
        }
    }
    return total;
}

The time complexity for generating all the subarrays is O(N^2)

## Contribution Technique
### Definition

Add the contribution of the individual element in the final answer.

Whenever you see the word, "**sum of all**" use contribution technique.

### Example1:
For the array **{3, 4, 2}**
| Element | Occurrence | Contribution |
|:-------:|:----------:|:------------:|
| 3 | 3 | 3 * 3 = 9 |
| 4 | 4 | 4 * 4 = 16 |
| 2 | 3 | 2 * 3 = 6 |
| | | Sum = 31 |

The sum of all the contributions is 31 which is the same as our previous answer.

### Example 2:

Given array, **{2, 8, -1, 4}**

| Starting Index | Ending Index | Subarray | Sum |
|:--------------:|:------------:|:-------------:|:---:|
| 0 | 0 | {2} | 2 |
| 0 | 1 | {2, 8} | 10 |
| 0 | 2 | {2, 8, -1} | 9 |
| 0 | 3 | {2, 8, -1, 4} | 13 |
| 1 | 1 | {8} | 8 |
| 1 | 2 | {8, -1} | 7 |
| 1 | 3 | {8, -1, 4} | 11 |
| 2 | 2 | {-1} | -1 |
| 2 | 3 | {-1, 4} | 3 |
| 3 | 3 | {4} | 4 |

The contribution here is as follows:

| element | occurrence | contribution (ele * occ) |
|:-------:|:----------:|:------------------------:|
| 2 | 4 | 8 |
| 8 | 6 | 48 |
| -1 | 6 | -6 |
| 4 | 4 | 16 |
| | | Sum = 66 |

### Example

| 0 | 1 | 2 | 3 | 4 | 5 |
|:---:|:---:|:---:|:---:|:---:|:---:|
| 3 | -2 | 4 | -1 | 2 | 6 |

### Intuition
- In how many subarrays a particular index will be present?
- In how many subarrays index 3 is present?

All the arrays that are going to contain elements at index 3 will either start with or before index 3.

Similarly, all the arrays that contain **index 3** have to end on or after index 3.

- Count of subarrays that start before index 3 or end after index 3 or start or end at index 3:

| start index | end index |
|:-----------:|:---------:|
| 0 | 3 |
| 1 | 4 |
| 2 | 5 |
| 3 | |

**Total subarrays = 4 * 3 = 12**

A general formula can be generated for ith index:

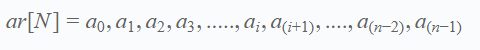
Count of subarrays with i^th^ index = (i + 1) * (N - i)
for ith index start = i + 1 end = n - i
subarrays ith index = (i + 1) * (N - i)

<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/046/058/original/Screenshot_2023-09-04_at_7.22.43_PM.png?1693835585" alt= “” width ="550" height="350">

### Example to verify results

Array : **{2, 8, -1, 4}**

| 0 | 1 | 2 | 3 |
| ------------- | ------------- | ------------- | ------------- |
| 2 | 8 | -1 | 4 |
| (0 + 1) * (4 - 0) | (1 + 1) * (4 - 1) | (2 + 1) * (4 - 2) | (3 + 1) * (4 - 3) |
| 2 * 4 = 8 | 8 * 6 = 48 | -1 * 6 = -6 | 4 * 4 = 16 |
| | | | Sum = 66 |

### Code

long subSum(int[] ar){
    int N = ar.length;
    long total = 0;
    for(int i=0; i < N; i++){
        long freq = (long)(i + 1) * (N - i);
        long con = freq * Arr[i];
        total = total + con;
    }
    return total;
}

Time Complexity: **O(N)**
Space Complexity: **O(1)**

## Problem : Return max subarray sum of len k
### Problem Statement

Given arr[N] elements, return Max subarray Sum of len = k

### Constraints

<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/050/772/original/Screenshot_2023-09-26_144518.png?1695719726" alt= “” width ="250" height="150">

### Example

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|:---:| --- | --- | --- | --- | --- | --- | --- | --- | --- |
| -3 | 4 | -2 | 5 | 3 | -2 | 8 | 2 | -1 | 4 |

### Dry Run

| start index | end index | sum |
|:-----------:|:---------:|:-------:|
| 0 | 4 | 7 |
| 1 | 5 | 8 |
| 2 | 6 | 12 |
| 3 | 7 | 16 |
| 4 | 8 | 10 |
| 5 | 9 | 11 |
| 6 | 10 | Invalid |

### Brute Force Approach and Psuedo Code
- For every subarray of len=k, iterate and get sum and get overall max.

### Pseudocode

long maxSum(arr[N], int k){

    int N = arr.length;
    int s = 0, e = k - 1;
    long ans = Long.MIN_VALUE;
    while(e < n){
        long sum = 0;
        for(int i = s; i <= e; i++){
            sum = sum + arr[i];
        }
        s = s + 1; e = e + 1;
        if(ans < sum) ans = sum;
    }
}

As the maximum sum of all the elements of the array may exceed the integer limit, we must use long to avoid unexpected values in the output.

**Note -** To find the minimum value initial variable has to be assigned the maximum infinity value and vice versa.

### Max Subarray Sum of length k : Optimal Approach

This problem is **Range query problem**, it can be solved using **prefix sum solution**.

Try to code it up, if confused you can take help from class recording.

## Sliding Window
### Definition

We can solve this problem without taking extra space using the Sliding Window approach.

In questions, if subarray size is fixed, we can use, Sliding Window technique.

### Example

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| --- | --- | --- | --- | --- | --- | ---- | ---- | ---- | --- |
| 3 | 4 | -2 | 5 | 3 | -2 | 8| 2 | 1| 4 |

k = 6

### Sliding Window Approach

<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/046/060/original/Screenshot_2023-09-04_at_7.25.33_PM.png?1693835748" alt= “” width ="500" height="400">

| start index | end index | sum | value |
|:-----------:|:--------- |:---------------------------------------------:|:---------------------:|
| 0 | 5 | arr[0] + arr[1] +arr[2] +arr[3]+arr[4]+arr[5] | 3 + 4 -2 + 5 + 3 = 11 |
| 1 | 6 | sum - arr[0] + arr[6] | 11 - 3 + 8 = 16 |
| 2 | 7 | sum - arr[1] + arr[7] | 16 - 4 + 2 = 14 |
| 3 | 8 | sum - arr[2] + arr[8] | 14 - (-2) + 1 = 17 |
| 4 | 9 | sum - arr[3] + arr[9] | 17 - 5 + 4 = 16 |

### Pseudo Code

long sub(int[] arr, int k){
    long ans = Long.MIN_VALUE;
    int N = arr.length;
    long sum = 0;
    for(int i = 0; i < k; i++){ // k iterations
        sum = sum + arr[i];
    }
    if(ans < sum){
        ans = sum; // 1st subarray
    }
    int s = 1, e = k;
    while(e < n){ // N - k + 1 
    //get subarray sum [s..e] using a sliding window
        sum = sum - arr[s - 1] + arr[e]
        if(ans < sum){ans = sum;}
        s++; e++;
    }
    return ans;
}

Time Complexity: **O(N)**
Space Complexity: **O(1)**