# Stacks
### Introduction to Stack
- Simple English word that refers to the stack or pile of things.
- It is a Linear Data Structure.
- Follows the Last In First Out(LIFO) or First In Last Out (FILO) principle.
- In recursion, we used call stack for function calls that execute the newest function first.
### Functions of Stacks
- add elements
- remove elements
- returns the size of the stack
- access elements on the top
```javascript
Stack<Integer> st = new Stack<>();
st.push(x); // add element
st.pop(); // remove element
st.size() // returns size of the stack;
st.peek(); // access the top element
```
### Problem Statement
Given a string str, remove equal pair of adjacent characters. Return the answer without adjacent duplicates.
#### Example
- **s = abbd** -> "ad"
- **s = abccbde** -> "ade"
- **s = abbbd** -> "abd"
- **s = abba** -> ""
#### Psuedo Code
```java
Stack<Character> st = new Stack<>();
String str = "abbcbbcacx";
int n = str.length();
for(int i = 0; i < n; i++){
char ch = str.charAt(i);
if(ch == st.peek()) st.pop();
else st.push(ch);
}
StringBuilder sb = new StringBuilder();
while(st.size() > 0){
sb.insert(0,st.pop());
}
return sb.reverse();
```
## Expression Evaluation
#### Mathematical Expression
- **Bodmas** defines Operators precedency, the execution order of operators.
- If two operators have the same precedence then we solve from **left to right**.
#### Infix expressions
- Operators(+, -, * , ...) between operands
- Operand1 Operator Operand2
#### Postfix expressions
- Operands between Operators(+, -, * , ...)
- Operand1 Operator Operand2
### Infix to Postfix expression
**Example 1**
- `a/(b-`**`(c-d)`**`+e*f)`
- `a/(b-(cd-)+`**`e*f`**`)`
- `a/(`**`b-(cd-)`**`+ef*) `
- `a/(`**`(bcd--)+ef*) `**
- **`a/(bcd--ef*+))`**
- **`abcd--ef*+/`**
**Example 2**
- `A+B/C*`**`(D+E)`**`-F`
- `A+`**`B/C`**`*DE+-F`
- `A+`**`BC/DE+*`**`-F`
- **`ABC/DE+*+`**`-F`
- **`ABC/DE+*+F-`**
### Infix to Postfix Conversion
- Dry run the above examples using a stack to convert the above infix expressions to postfix expressions.
### Procedure
1. If the **character is operand**, then add it to postfix string
2. If the **character is (** (opening bracket), push it to the stack.
3. If the **character is )** (closing bracket), pop all the operators and add them to the postfix string until and unless we encounter the opening bracket. Pop the opening bracket from the stack.
4. If **character is operator**
```java
while((st.size() > 0) && (st.peek() != '(') && (priority(st.peek()) >= priority(current element))){
char character = st.pop();
postfix.append(character);
}
if((st.size() == 0) || (st.peek() == '(') || (priority(st.peek() < priority(current element)))){
st.push(ch)
}
```
5. If **all the characters from the string are read** then pop all the operators from the stack and insert them in postfix.
### Priority Function
```java
int priority(char ch){
if(ch == '+' || ch == '-') return 1;
else if(ch == '*' || ch == '/') return 2;
else return 3;
}
```
### Problem : Nearest smaller on left
Given an `arr[N]`, for every element `arr[i]` find nearest smaller element on left side.
**Note:** Nearest element `arr[i]` distance between indices.
#### Example 1
```java
arr[6]: [4, 5, 2, 10, 3, 12]
ans[6]: [-1, 4, -1, 2, 3, 3]
```
#### Example 2
```java
arr[8]: [4, 6, 10, 11, 7, 8, 3, 5]
ans[8]: [-1, 4, 6, 10, 6, 7, -1, 3]
```
#### Brute force idea
For every element iterate on the left and get nearest smaller on left.
**Pesudocode**
```java
int[] findNearestSmallerElements(int arr[N]) {
int ans[N] = {-1};
for (int i = 0; i < n; i++) {
for (int j = i - 1; j >= 0; j--) {
if (arr[j] < arr[i]) {
ans[i] = arr[j];
break;
}
}
}
return ans;
}
```
#### Time and Space Complexity
What will be T.C and S.C for the above approach?
* **TC -** $O(N^2)$
* **SC -** O(1)
#### Optimized Solution
We can optimize the solution using the **Stack** data structure.
#### Example 1
```java
arr[12]: [5, 8, 11, 14, 7, 10, 13, 6, 9 , 10, 2, 5]
ans[12]: [-1, 5, 8, 11, 5, 7, 10, 5, 6, 9, -1, 2]
```

#### Example 2
```java
arr[12]: [4, 6, 10, 11, 6, 8, 3, 5]
ans[12]: [-1, 4, 6, 10, 4, 6, -1, 3]
```

**Pesudocode**
```java
int[] findNearestSmallerElements(int[] arr) {
int n = arr.length;
int[] ans = new int[n];
Stack<Integer> st = new Stack<>();
for (int i = 0; i < n; i++) {
while (!st.isEmpty() && st.peek() >= arr[i]) {
st.pop();
}
if (!st.isEmpty()) {
ans[i] = st.peek();
} else {
ans[i] = -1;
}
st.push(arr[i]);
}
return ans;
}
```
#### Time and Space Complexity
What will be T.C and S.C for the above approach?
* **TC -** O(N)
* **SC -** O(N)
### Problem Statement : Next smaller index on left
Given an `arr[N]`, for every element `arr[i]` find nearest smaller index on left side.
#### Example 1
```java
arr[8]: [4, 6, 10, 11, 7, 8, 3, 5]
ans[8]: [-1, 0, 1, 2, 1, 4, -1, 6]
```

**Pesudocode**
```java
int[] findNearestSmallerElements(int[] arr) {
int n = arr.length;
int[] ans = new int[n];
Stack<Integer> st = new Stack<>();
for (int i = 0; i < n; i++) {
while (!st.isEmpty() && arr[st.peek()] >= arr[i]) {
st.pop();
}
if (!st.isEmpty()) {
ans[i] = st.peek();
} else {
ans[i] = -1;
}
st.push(i);
}
return ans;
}
```
#### Time and Space Complexity
What will be T.C and S.C for the above approach?
* **TC -** O(N)
* **SC -** O(N)
### Problem Statement - Nearest Greater index on right
Given an `arr[N]`, for every element `arr[i]` find nearest greater index on right side.
**Pesudocode**
```java
int[] findNearestGreaterElements(int[] arr) {
int n = arr.length;
int[] ans = new int[n];
Stack<Integer> st = new Stack<>();
// Iterate from right to left
for (int i = n - 1; i >= 0; i--) {
while (!st.isEmpty() && arr[st.peek()] <= arr[i]) {
st.pop();
}
if (!st.isEmpty()) {
ans[i] = st.peek();
} else {
ans[i] = -1;
}
st.push(i);
}
return ans;
}
```
#### Time and Space Complexity
What will be T.C and S.C for the above approach?
* TC - O(N)
* SC - O(N)
### Hands on exercise :
By refering above questions, Please try the other variants also :
* Given an arr[N], for every element arr[i] find nearest smaller index on right side.
* Given an arr[N], for every element arr[i] find nearest greater element on left side.
### Problem Statement - Largest Area Histogram
Given continous block of Histogram find max rectangle area which can be present with in histograms.
**Note:** Every Histogram is of `width = 1`.
This question has been previously asked in *Adobe*, *Amazon*, *Microsoft*, *Uber*, *Bloomberg*, and *Facebook*.
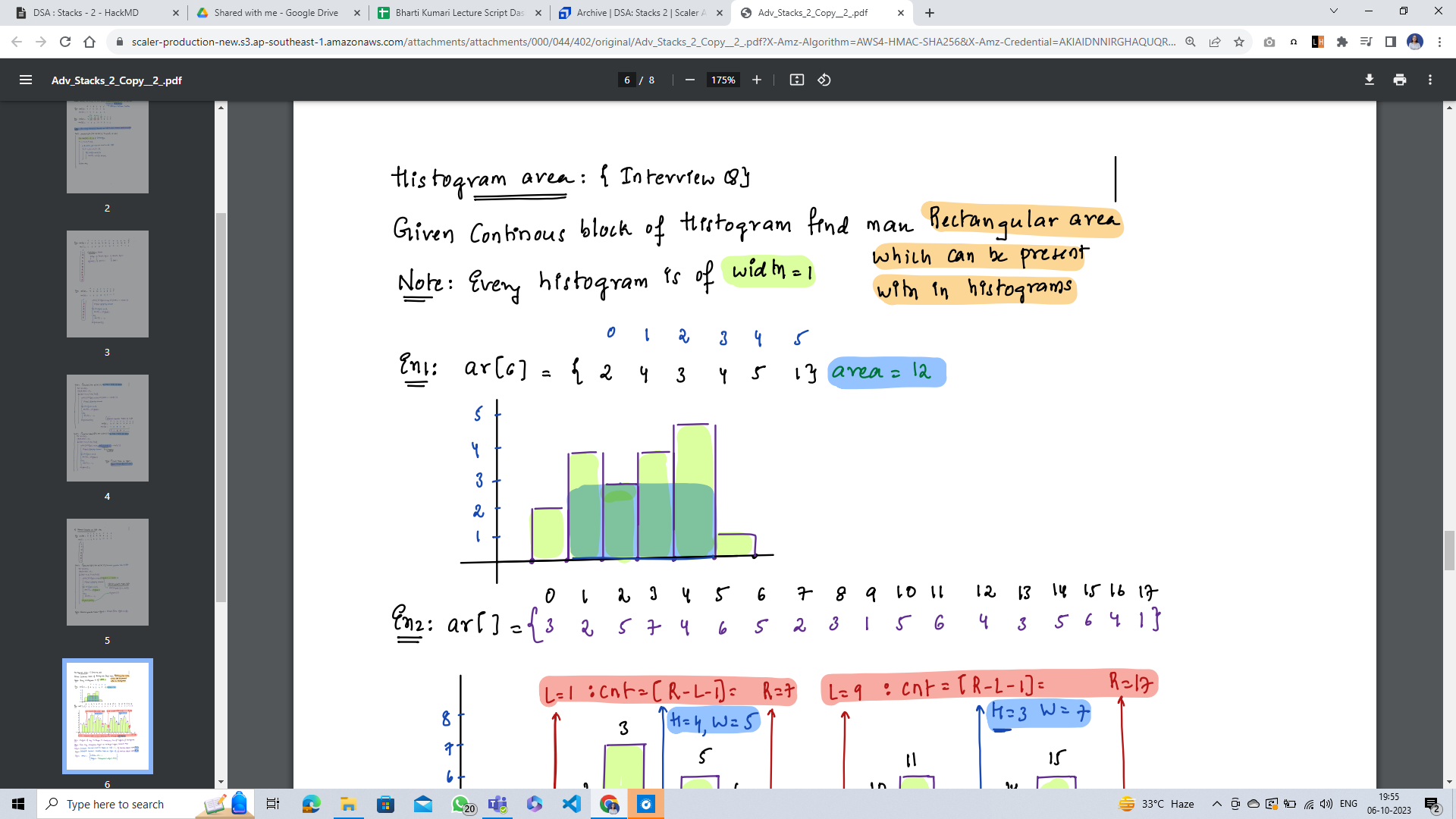
#### Example 1
```java
arr[6]: [2, 4, 3, 4, 5, 1]
area = 12
```
#### Example 2
```javascript
arr[18]: [3, 2, 5, 7, 4, 6, 5, 2, 3, 1, 5, 6, 4, 3, 5, 6, 4, 1]
area = 21
```
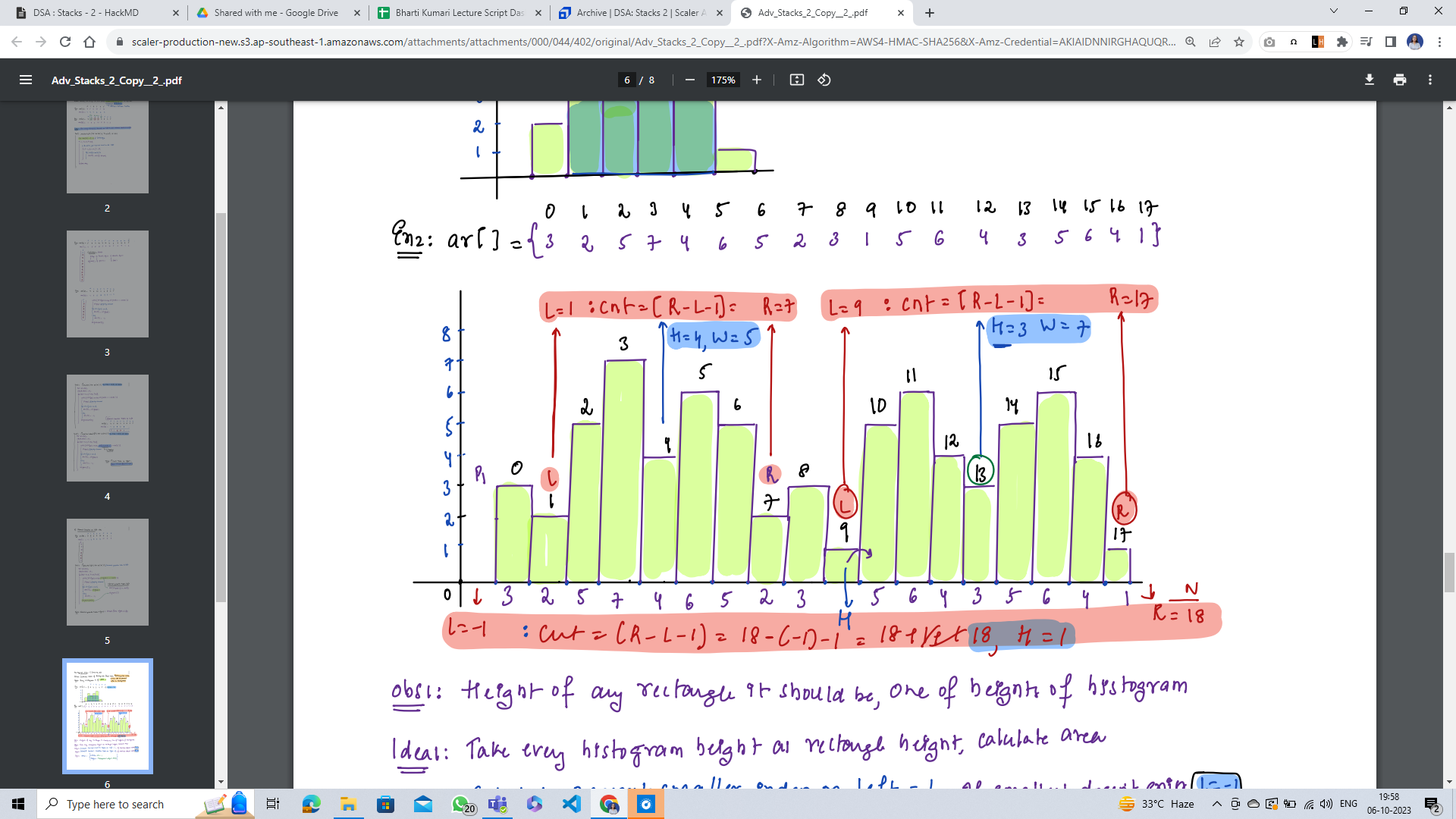
#### Observation
Height of any rectangle, it should be one of the heights of histogram.
#### Idea
Take every histogram height as rectangle height and calculate area.
>**Step 1:** Calculate first smaller index on left = L.
**Step 2:** Calculate first smaller index on right = R.
**Step 3:** are = [width = R - L - 1, Height = Histogram height arr[i]]
**Pseudocode**
```java
int[] getMaxRectangleArea(int heights[n]) {
int L = nearestSmallerIndexLeft(heights);
int R = nearestSmallerIndexRight(heights);
int ans = 0;
for(int i = 0; i < n; i++) {
int h = heights[i];
int w = R[i] - L[i] - 1;
if(ans < h * w) {
ans = h * w;
}
}
return ans;
}
```
#### Time and Space Complexity
What will be T.C and S.C for the above approach?
* TC - O(N)
* SC - O(N)
# Queues
### Explanation
Queue is a data structure that works like a line of people waiting for something. Imagine you have a line at a ticket counter or a supermarket checkout. The first person to join the line is the first one to get served, and new people join at the end of the line. Similarly, the first element added to a queue is the first one to be removed, and new elements are added to the back of the queue.
A queue follows the **"First-In-First-Out" (FIFO)** principle, which means that the element that has been in the queue the longest is the first one to be processed, and the newest element added will have to wait until all the elements in front of it have been processed and removed.
Functions of queue involves:
* **Enqueue:** Adding an element to the rear (end) of the queue.
* **Dequeue:** Removing the front (first) element from the queue.
* **Front:** Accessing the element at the front (first) of the queue without removing it.
* **Rear:** Accessing the element at the rear (end) of the queue without removing it.
Each of these functions takes `O(1)` time for its operations.
Let's use the numbers 8, 14, 9, 20, and 30 to perform the queue operations:
Initial Queue: (empty queue)
**Enqueue (Adding to the queue):**
* Enqueue 8: Queue: [8]
* Enqueue 14: Queue: [8, 14]
* Enqueue 9: Queue: [8, 14, 9]
* Enqueue 20: Queue: [8, 14, 9, 20]
* Enqueue 30: Queue: [8, 14, 9, 20, 30]
**Dequeue (Removing from the queue):**
* Dequeue: The first element 8 is removed. Queue: [14, 9, 20, 30]
* Dequeue: The first element 14 is removed. Queue: [9, 20, 30]
**Front (Viewing the front element without removing it):**
The front element of the queue is 9.
**Rear (Viewing the rear element without removing it):**
The rear element of the queue is 30.
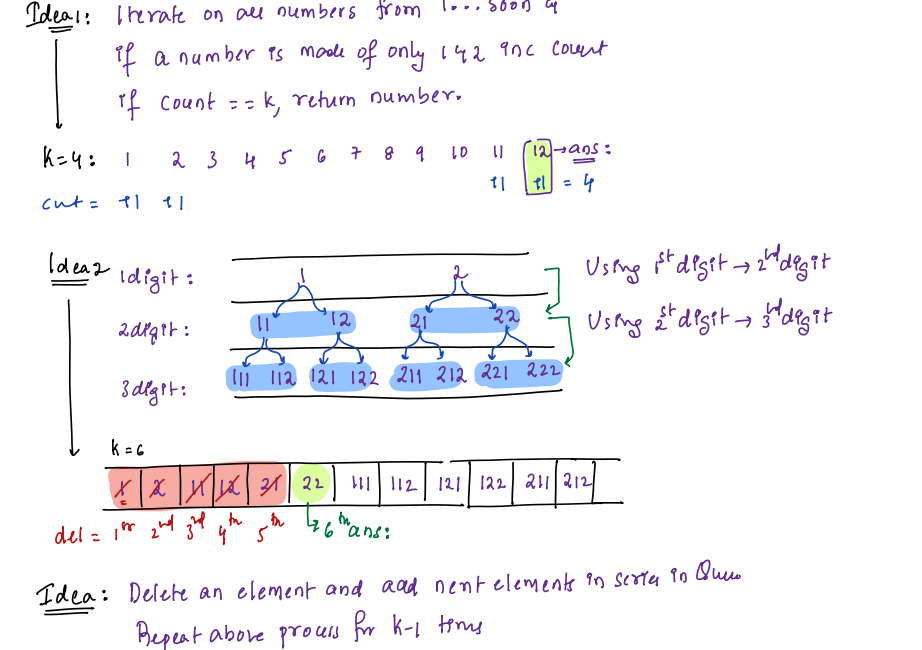
### Problem : Generate numbers using 1 & 2
Generate k-th number of the series using digits only 1 or 2. In this the input will be k
**For K=5**
* Start with an empty queue and enqueue the initial numbers 1 and 2.
* Queue: [1, 2]
* Dequeue the front number (1) and generate two new numbers by appending 1 and 2 to it.
* Enqueue: [2 (enqueue 12), 1 (enqueue 11)]
* Dequeue the front number (2) and generate two new numbers by appending 1 and 2 to it.
* Enqueue: [1 (enqueue 11), 12 (enqueue 112), 11 (enqueue 111)]
* Dequeue the front number (1) and generate two new numbers by appending 1 and 2 to it.
* Enqueue: [12 (enqueue 112), 11 (enqueue 111), 11 (enqueue 1111), 112 (enqueue 1112)]
* Dequeue the front number (12) and generate two new numbers by appending 1 and 2 to it.
* Enqueue: [11 (enqueue 111), 11 (enqueue 1111), 112 (enqueue 1112), 111 (enqueue 11111), 112 (enqueue 11112)]
* Now, the queue contains all numbers in the series up to the 5th position.
* The k-th number in the series is the last dequeued number before reaching k. In this case, the 5th number is "21".
The approach uses a queue to generate the series efficiently. Starting with the initial numbers 1 and 2 in the queue, we dequeue each number, append 1 and 2 to it, and enqueue the newly generated numbers back into the queue. This process is repeated k-1 times (since we already have the 1st and 2nd numbers). The k-th number is then the last number dequeued before reaching k iterations. This way, we efficiently generate the k-th number in the series using digits 1 or 2.
**Code for k-th Number**
```cpp
#include <iostream>
#include <queue>
#include <string>
using namespace std;
string kthNumber(int k) {
if (k <= 0) {
return ""; // Invalid input, return an empty string
}
if (k == 1) {
return "1"; // The 1st number in the series is always "1"
}
if (k == 2) {
return "2"; // The 2nd number in the series is always "2"
}
queue<string> q;
q.push("1");
q.push("2");
string kthNumber;
for (int i = 0; i < k - 2; i++) {
string currentNumber = q.front();
q.pop();
q.push(currentNumber + "1");
q.push(currentNumber + "2");
kthNumber = currentNumber;
}
return kthNumber;
}
```
**Time Complexity (TC):**
* The initialization part of the function (handling invalid inputs and the first two numbers) takes constant time, which can be considered as `O(1)`.
* The main loop runs k-2 times, where k is the input number. Within each iteration, the queue operations (enqueue and dequeue) take constant time, as they involve adding/removing elements from the front/rear of the queue.
Therefore, the overall time complexity is **O(k)**, as the main loop iterates k-2 times, and each iteration takes constant time.
**Space Complexity (SC):**
* The space required for the queue: At any point, the queue will contain at most k-2 elements. During the loop, we enqueue and dequeue elements, but the maximum number of elements in the queue remains k-2.
* Other than the queue, we use some additional variables like kthNumber, which are constant in terms of space complexity.
Therefore, the overall space complexity is **O(k)**, as the maximum space used by the queue is k-2, and the additional variables take constant space.
# Sliding Window Maximum
### Problem Statement
Given an integer array `A` and an window of size k find the max element.
### Example
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/053/902/original/upload_4c4499c78441c8180afcf468db0c57f4.png?1697475913"/>
### Question Explanation
Find max elements in 4-element sliding windows of array A:
- `[1, 8, 5, 6]` -> max: 8
- `[8, 5, 6, 7]` -> max: 8
- `[5, 6, 7, 4]` -> max: 7
- `[6, 7, 4, 2]` -> max: 7
- `[7, 4, 2, 0]` -> max: 7
- `[4, 2, 0, 3]` -> max: 4
Result: `[8, 8, 7, 7, 7, 4]`.
1. Initialize an empty list `max_elements`.
2. Iterate from index 0 to 3 (inclusive) to create windows of size 4.
3. Find the maximum element in each window and append it to `max_elements`.
4. Result: `[8, 8, 7, 7, 7, 4]`, representing max elements in each 4-element window in `A`.
### Dry Run using the Sliding Window Approach
Array `A = [1, 8, 5, 6, 7, 4, 2, 0, 3]` and `k = 4`.
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/053/903/original/upload_c51f03fd7ab32785b5087c21a5d907e3.png?1697475979"/>
Let's dry run the code with the given example:
Array `A = [1, 8, 5, 6, 7, 4, 2, 0, 3]` and `k = 4`.
1. Initialize an empty queue `q`.
2. Start iterating through the array elements.
- **For i = 0, A[i] = 1:**
- Queue `q` is empty, so nothing happens.
- Enqueue `i` at the rear of the queue. `q = [0]`.
- **For i = 1, A[i] = 8:**
- The front element of the queue is at index `0`, which is smaller than the current element and thus can't be the maximum for any window.
- Deque the element and Enqueue `i` at the rear of the queue. `q = [1]`.
- **For i = 2, A[i] = 5:**
- `q` is not empty, and `A[r]` (element at index `1`) is greater than `A[i]`, so we don't do anything.
- Enqueue `i` at the rear of the queue. `q = [2]`.
- **For i = 3, A[i] = 6:**
- `q` is not empty, and `A[r]` (element at index `2`) is smaller than `A[i]`, so we deque it, now 8 is greater than 6 so don't do anything.
- Enqueue `i` at the rear of the queue. `q = [3]`.
After the first K insertions, the q = [8,6];
Now the maximum of this window is present in the front so print it and slide the window.
- Continue this process for the remaining elements.
- Note: If current window start index > front of queue, it means front element of queue is out window, hence remove it.
3. The final output will be the maximum elements in each group of size `k`:
- For `k = 4`, the maximum elements are `[8, 8, 7, 7, 4, 2, 3]`.
So, the dry run demonstrates how the code finds and prints the maximum elements in groups of size `k` as it iterates through the array.
### Pseudocode (Using Dequeue)

* **Time complexity:** O(n)
* **Space Complexity:** O(n)
# Linked List Basics
- Here we are creating a `Node` class which has an attribute named `data` and an object reference `next` which stores the address of the next Node object.
- Inside the constructor, we are passing the value which is stored into the `data` variable and next will always be null for the newly created node.
```cpp
class Node{
int data; // variable
Node next; // object reference -> hold address of Node object
Node(int x){ // constructor -> used to initialize data members of class
data = x;
next = NULL;
}
}
main(){
Node h = new Node(30);
// ref // object creation
print(h.data); // prints 30
print(h.next); // prints null
print(h); // prints address of Node i.e. ad1
}
```
# Printing linked list
```cpp
t=h; // ad1
while(t!=null){
print(t.data); // 30 40 50 60
t=t.next; // ad2 ad3 ad4 null
}
```
- First of all, we are storing the `h` in `t`, so `ad1` will be stored in `t`.
- Then we are printing the data in `t`, which prints `30`.
- After that `t=t.next;` stores the `ad2` in the t, as we have `ad2` in `t.next`.
- Again we will print the data of `t`, then it prints `40`,
- `t=t.next=ad3`.
- Prints `t.data` i.e. `50`
- `t=t.next=ad4`
- Print `t.data` i.e. `60`
- `t=t.next=null`
- As now `t` becomes `null`, so now loop will terminate.
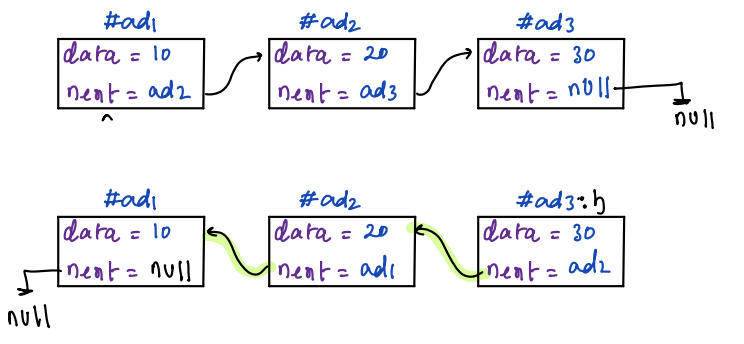
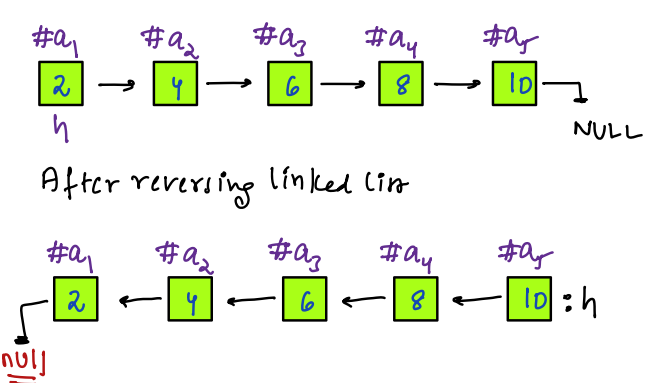
# Reverse Linked List
Given a Linked List, reverse the entire linked list and return the head node. We can only change the reference of the node.
**Note:** No extra space will be used and we cannot change the value of the node.
## Example 1
## Example 2
## Idea
Insert every node at the start of the list one by one.
Suppose we have a linked list, **20->15->10->5->null**.
- So first insert 20 at starting

- Now again insert the next node i.e. 15 at the start.
- In this way insert nodes one by one at the start.
## Observation
Nodes inserted at the start gives us the reverse order of the linked list.
## Trace
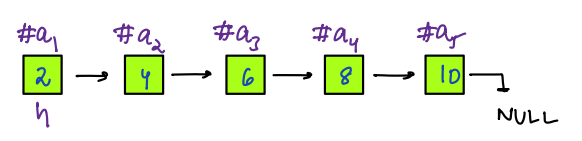
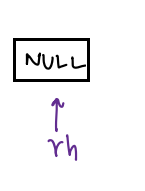
- Initially, we don't have any node in the reversed list, so we are taking `rh=null`.
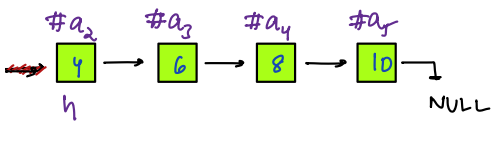
- Now,
```cpp
Node t=h;
h = h.next;
t.next = rh;
rh = t;
```
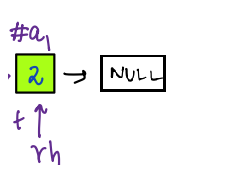
- Now continue this process.
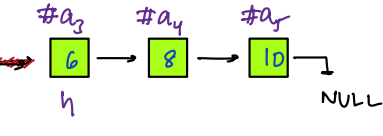
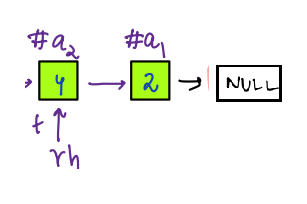
- Similarly, we continue this process till `h!=null`.
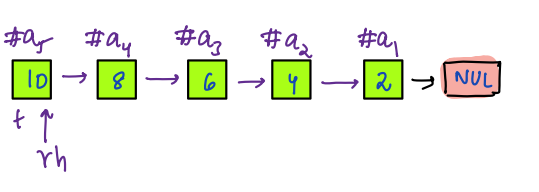
- At last, we will return `rh` as it contains the address of the first node of reversed linked list.
## PseudoCode
```cpp
Node reverse(Node h){
Node rh = null;
while(h!=NULL){
Node t = h;
h = h.next;
t.next = null;
t.next = rh;
rh = t;
}
return rh;
}
```
# Middle of the Linked List
Given the head node, return the mid of the linked list.
## Example 1
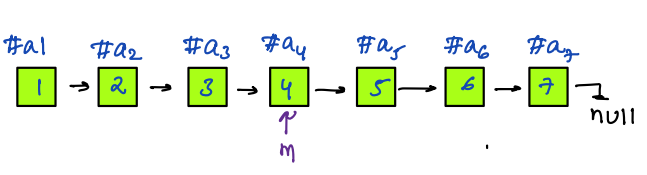
## Example 2
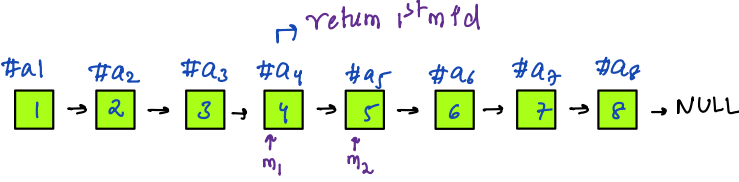
**In case of two mids(when length of linked list is even), return 1st mid**
## Idea 1
**Step 1:** Iterate and calculate the length of the linked list and store it in `N` and initialize `t=h`.
**Step 2:** Iterate till `N/2` and update `t=t.next`.
**Step 3:** Return t.
## Complexity
**Time Complexity:** O(N)
**Space Complexity:** O(1)
But here we are using two loops.
## Idea 2
**Find mid in a single loop.**
1. Take `slow` and `fast` and initialize both of them by `head`.
1. slow = slow.next // move slow one step
2. fast = fast.next.next // move fast two steps
- `slow` reached the centre when `fast.next==null` in case of odd length.
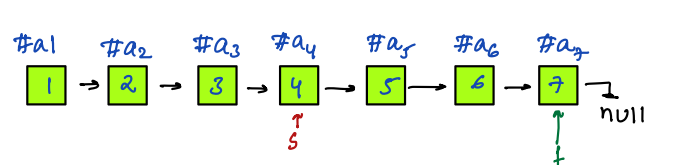
- `slow` reached the centre when `fast.next.next==null` in case of even length.

## Observation
Use both conditions `fast.next!=null && fast.next.next!=null`, so our code will work for both odd and even-length linked lists.
## PseudoCode
```cpp
Node mid(Node h){
Node slow = h;
Node fast = h;
// if linked list is empty
if(h == null)
{
return null;
}
while(fast.next!=null && fast.next.next!=null){
slow = slow.next;
fast = fast.next.nextl
}
return slow;
}
```
# Merge Two sorted linked lists
Given two sorted linked lists, merge and find a final sorted list.
## Understanding the Problem Statement
Arrange the two given sorted linked lists, to get a final linked list by merging both input lists in a sorted order.
## Example 1
**Input:**
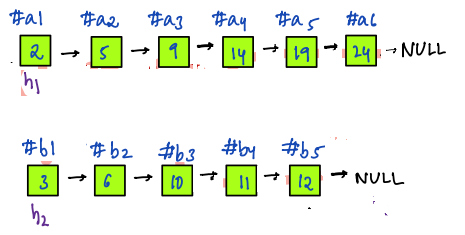
**Output:**

**Explanation:**
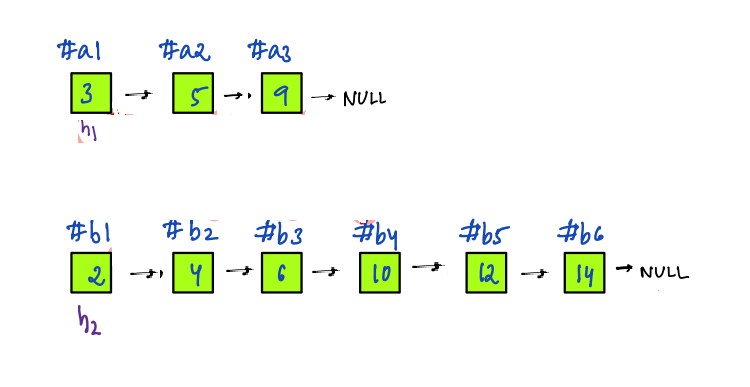
- We have the `#a1` node with the smallest value i.e. `2`, so it becomes the first node of the final linked list.
- After this, we have a `#b1` node with the smallest value i.e. `3` among all the available nodes.
- After that, we have `#a2` with the value `5`.
- In this way, we will arrange all the nodes of the input linked lists in ascending order of their values.
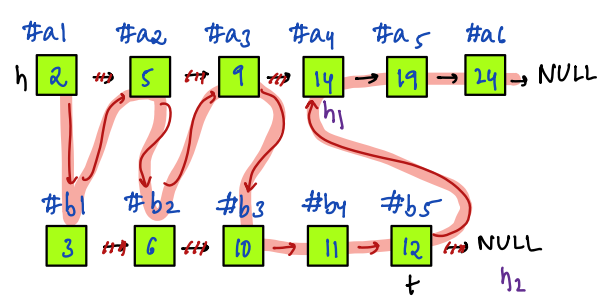
## Example 2
**Input:**
**Output:**

## Idea
How we can merge two sorted arrays? We follow the same for merging two sorted linked lists, so we can easily merge two sorted arrays by using two pointer approach, now we will use two pointer approach for merging two sorted linked lists.
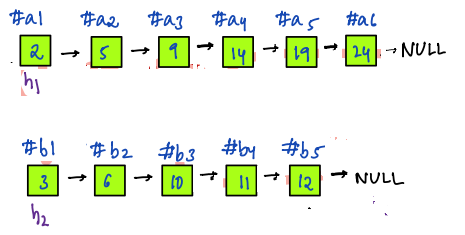
- We'll create a starting node called `h` and use a pointer called `t`.
- At first, we initialize the `h` and `t` by the node having a smaller value among the `h1` and `h2` nodes.
- After that at each iteration of the loop, we compare the values of the nodes at `h1` and `h2`, and point `t.next` to the smaller value node. Then we advance the pointer `t` and pointer of that smaller value node list and repeat this process until one of the list pointers reaches the end of the list.
- At this point, there's no need to iterate through the rest of the other list because we know that it's still in sorted order. So `t.next = h1 or h2` points `t.next` to the list that still has nodes left. The last step is just to return `h`.
## Complexity
- **Time Complexity:** O(N+M)
- **Space Complexity:** O(1)
# Cycle detection
Given a head node of a linked list, check for the cycle.
## Understanding the Problem Statement
In the linked list, the last node points to the null, but instead of pointing to the null if the last node points to any other node of the linked list, then we have a cycle in a linked list.
## Example 1
**Input:**
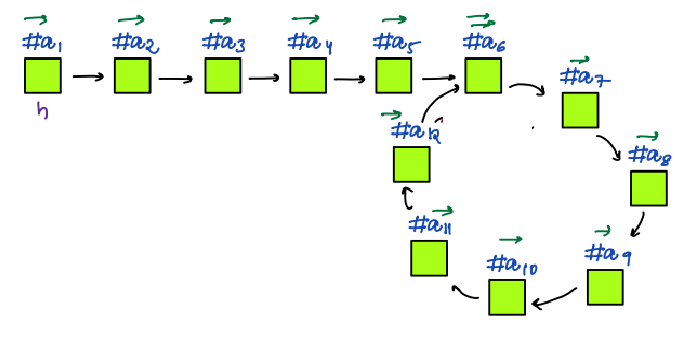
**Output:**
Yes
**Explanation:**
We have a cycle in the input linked list, as the last node i.e. `#a12` instead of pointing to `null`, pointing to the node `#a6`.
## Example 2
**Input:**
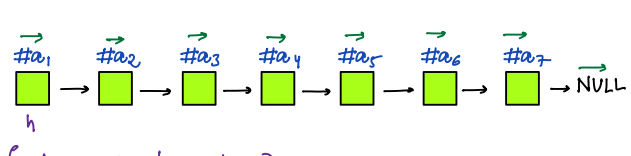
**Output:**
No
**Explanation:**
We don't have a cycle in the input linked list, as the last node i.e. `#a7` points to the `null` node.
## Idea
- Take the `slow` and `fast` pointer, and initialize both by `head` node.
- Move `slow=slow.next` and `fast=fast.next.next`.
- If `slow==fast`, then there is a cycle.
- If `fast.next==null && fast.next.next==null`, then we have reached the end of the linked list and this means there is no cycle in the linked list.
## PseudoCode
```java
boolean detectCycle(Node h){
Node slow = h, fast = h;
if(h==NULL) {
return false;
}
boolean isCycle = false;
while(fast.next != NULL && fast.next.next != NULL){
slow = slow.next;
fast = fast.next.next;
if(slow == fast){
isCycle = true;
break;
}
}
return isCycle;
}
```
## Complexity
- **Time Complexity:** O(N)
- **Space Complexity:** O(1)
# Comparator
* In programming, a **comparator** is a function that compares two values and returns a result indicating whether the values are equal, less than, or greater than each other.
* The **comparator** is typically used in sorting algorithms to compare elements in a data structure and arrange them in a specified order.
**Comparator** is a function that takes **two arguments**.
For languages - **Java, Python, JS, C#, Ruby**, the following logic is followed.
```
1. In sorted form, if first argument should come before second, -ve value is returned.
2. In sorted form, if second argument should come before first, +ve value is returned.
3. If both are same, 0 is returned.
```
For **C++**, following logic is followed.
```
1. In sorted form, if first argument should come before second, true is returned.
2. Otherwise, false is returned.
```
## Sorting based on Factors
### Problem Statement
Given an array of size n, sort the data in ascending order of count of factors, if count of factors are equal then sort the elements on the basis of their magnitude.
### Example 1
```plaintext
A[ ] = { 9, 3, 10, 6, 4 }
Ans = { 3, 4, 9, 6, 10 }
```
**Explanation:**
Total number of factors of 3, 4, 9, 6, 10 are 2, 3, 3, 4, 4.
### C++
```cpp
int factors(int n)
{
int count = 0;
int sq = sqrt(n);
// if the number is a perfect square
if (sq * sq == n)
count++;
// count all other factors
for (int i=1; i<sqrt(n); i++)
{
// if i is a factor then n/i will be
// another factor. So increment by 2
if (n % i == 0)
count += 2;
}
return count;
}
bool compare(int val1, int val2)
{
int cnt_x = count_factors(x);
int cnt_y = count_factors(y);
if(factors(val1) == factors(val2))
{
if(val1<val2)
{
return true;
}
return false;
}
else if(factors(val1)<factors(val2))
{
return true;
}
return false;
}
vector<int> solve(vector<int> A) {
sort(A.begin() , A.end() , compare);
return A;
}
```
### Python
```cpp
import functools
//please write the code for finding factors by yourself
def compare(v1, v2):
if(factors(v1) == factors(v2)):
if(v1<v2):
return -1;
if(v2<v1):
return 1;
else
return 0;
elif (factors(v1)<factors(v2)):
return -1;
else
return 1;
class Solution:
def solve(self, A):
A = sorted(A, key = functools.cmp_to_key(compare))
return A
```
### Java
```cpp
//please write the code for finding factors by yourself
public ArrayList<Integer> solve(ArrayList<Integer> A) {
Collections.sort(A, new Comparator<Integer>(){
@Override
public int comp(Integer v1, Integer v2){
if(factors(v1) == factors(v2)){
if(v1<v2) return -1;
else if(v2<v1) return 1;
return 0;
}
else if(factors(v1)<factors(v2)){
return -1;
}
return 1;
}
});
return A;
}
```
## B Closest Points to Origin
### Problem Statement
Given an array of points where points[i] = [xi, yi] represents a point on the X-Y plane and an integer k, return the B closest points to the origin (0, 0).
The distance between two points on the X-Y plane is the Euclidean distance (i.e., $√(x1 - x2)^2 + (y1 - y2)^2$).
You may return the answer in any order.
**Example 1:**
><img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/057/739/original/Screenshot_2023-11-23_at_4.01.31_PM.png?1700735500" width=300/>
>**Input:** points = [[1,3],[-2,2]], B = 1
**Output:** [[-2,2]]
**Explanation:**
The distance between (1, 3) and the origin is sqrt(10).
The distance between (-2, 2) and the origin is sqrt(8).
Since sqrt(8) < sqrt(10), (-2, 2) is closer to the origin.
We only want the closest B = 1 points from the origin, so the answer is just [[-2,2]].
**Example 2:**
>**Input:** points = [[3,3],[5,-1],[-2,4]], B = 2
**Output:** [[3,3],[-2,4]]
**Explanation:** The answer [[-2,4],[3,3]] would also be accepted.
## B Closest Points to Origin Approach
We find the B-th distance by creating an array of distances and then sorting them using custom sorting based on distances from origin or points.
After, we select all the points with distance less than or equal to this K-th distance.
### Logic for Custom Sorting
Say there are two points, (x1, y1) and (x2, y2),
The distance of (x1, y1) from origin will be ${sqrt((x1-0)^2 + (y1-0)^2)}$
The distance of (x2, y2) from origin will be ${sqrt((x2-0)^2 + (y2-0)^2)}$
We can leave root part and just compare $(x1^2 + y1^2) and (x2^2 + y2^2)$
#### Below logic works for languages like - Java, Python, JS, ...
```cpp
// Need to arrange in ascending order based on distance
// If first argument needs to be placed before, negative gets returned
if((x1*x1 + y1*y1) < (x2*x2 + y2*y2))
return -1;
// If second argument needs to be placed before, positive gets returned
else if ((x1*x1 + y1*y1) > (x2*x2 + y2*y2))
return 1;
// If both are same, 0 is returned
else return 0
---------------------------------------------
// Instead of writing like above, we could have also written
return ((x1*x1 + y1*y1) - (x2*x2 + y2*y2))
```