<style> section { text-align: left; } .reveal .slides section { font-size: 30px; } </style> # Presentation on Round Asynchronous Amnesiac Flooding (RAAF) <!-- Put the link to this slide here so people can follow --> Slide: https://hackmd.io/@tobi-alafin/BJuF8I9i0 ## Statement of Ethical Compliance This project complies with the [ethical guidelines](https://canvas.liverpool.ac.uk/courses/68389/pages/ethical-guidance-2) set forth by the Department of Computer Science under the School of Electrical Engineering, Electronics and Computer Science at the University of Liverpool. Based on the nature of the research, which is primarily theoretical and does not involve human/animal participants or sensitive data, this project falls under the **A0** category of ethical review. ---- ## Generative AI Usage Disclaimer - Extensive use of large language models (LLMs) throughout the project - Primarily Claude 3.5 Sonnet and GPT-4/o - Used as: - Research assistants, sounding boards, and communication aids - Tools for refining ideas, arguments, notes, and drafts - Assistants for paper comprehension and literature summarisation - Did not use LLMs to wholly write dissertation, presentation slides or project proposal - Usage complies with [school's guidance on generative AI](https://www.liverpool.ac.uk/media/livacuk/centre-for-innovation-in-education/digital-education/generative-ai-teach-learn-assess/guidance-on-the-use-of-generative-ai.pdf) --- # Introduction - Amnesiac Flooding (AF): A variant of classical flooding - Nodes don't retain memory beyond the previous round - Round-Asynchronous Amnesiac Flooding (RAAF) - Introduces adversarial delays into AF model - Motivation: Understanding flooding in realistic network scenarios - Message delays are common - Potential for manipulation by malicious actors --- ## Seminal Work: "On the Termination of a Flooding Process" - First formal analysis[1] of Amnesiac Flooding - Key results for synchronous AF: - Termination guaranteed on finite graphs - For bipartite graphs: terminates in exactly $e$ rounds - $e$ is the eccentricity of the source node - For non-bipartite graphs: terminates between $e$ and $e+d+1$ rounds - $d$ is the diameter of the graph - Asynchronous setting: - Showed non-termination possible with adaptive adversary --- ## Our Contributions - Formal model for Round-Asynchronous Amnesiac Flooding (RAAF) - Precise, formal protocol description - Enables non-trivial technical statements and rigorous proofs - Termination analysis: - Proved termination guarantees for acyclic graphs - Demonstrated non-termination strategies for all cyclic graphs - Decidability results: - Proved undecidability of termination for arbitrary computable adversaries - Constructed Periodic Finite State Adversary (PFSA) model - Makes termination decidable --- # Model Definition - Operates on finite, connected graph $G = (V, E)$ - Initial node $g_0 \in V$ - Message set $\mathcal{M}$ - Time proceeds in discrete rounds $R_1, R_2, \ldots$ ---- ## State Record For each node $u \in V$ in round $j$: $$ \text{StateRecord} = (M, s, d, p) $$ Where: - $M \subseteq \mathcal{M}$: set of messages held by the node - $s: \mathcal{M} \to \mathcal{P}(V)$: source map - $d: \mathcal{M} \to \mathcal{P}(V)$: destination map - $p: \mathcal{M} \to \mathbb{Z}^k$: priority function ---- ## State Function $$ S: \mathbb{N} \to (V \to \text{StateRecord}) $$ - Where $S(i)(v)$ represents the state of node $v$ at round $i$. - Note: This is a function from the round number to another function that maps each node to its state record. ---- ## Round Function $$ r : \mathbb{N} \to \mathcal{M} \to \mathcal{P}(V \times E) $$ - Where $r(i)(m)$ is the set of (sender node, edge) pairs over which $m \in \mathcal{M}$ is transmitted in the $i$-th round - Note: this function maps each round to a function that maps each message to the set of sender node and edge pairs over which the message was **actually** transmitted after delays have been applied. --- ## Adversary Delay Function $$d: G \to (\mathbb{N} \times V \times E \to \{0, 1\})$$ - $d(G)(j, u, e) = 1$: message from node $u$ along edge $e$ is delayed in round $j$ - $d(G)(j, u, e) = 0$: message is delivered --- ## Round Process For each round $R_j$, and node $u \in V$: 1. Adversary applies delays 2. Messages sent based on previous round's state (destination maps) and applied delays 3. Messages received, source message map updated 4. Messages retained (cache management, priorities updated) 5. Delivery intentions set for next round (destination-message map updated) Note: Sending and receiving are conceptually simultaneous, but have logical dependencies --- ## State Update Rules $$ S(j+1)(u)[3] = g: \mathcal{M} \to \mathcal{P}(V) $$ Where for each message $m \in \mathcal{M}$: $$ g(m) = \begin{cases} X_{\text{retained}} & \text{if } m \in S(j)(u)[1] \cap S(j+1)(u)[1] \\ X_{\text{new}} & \text{if } m \in S(j+1)(u)[1] \setminus S(j)(u)[1] \\ \emptyset & \text{if } m \notin S(j+1)(u)[1] \end{cases} $$ ---- With $X_{\text{retained}}$ and $X_{\text{new}}$ defined as: $$ X_{\text{retained}} = \{v \in V \mid v \in S(j)(u)[3](m) \text{ and } d(G)(j+1, u, \{u,v\}) = 1\} $$ $$ X_{\text{new}} = \{v \in V \mid \{u, v\} \in E \text{ and } v \notin S(j+1)(u)[2](m)\} $$ --- ## Termination Given a connected graph $G = (V, E)$ with a set of messages $\mathcal{M}$, and the round function $r: \mathbb{N} \to (\mathcal{M} \to \mathcal{P}(V \times E))$: 1. **Termination Condition**: The flooding process is considered terminated if and only if there exists a round $t$ such that for all rounds $k > t$, all nodes $u \in V$ and for all messages $m \in \mathcal{M}$: $$ r(k)(m) = \emptyset \land S(k)(u)[1] = \emptyset $$ 2. **Termination Round**: The termination round $t_{\text{min}}$ is defined as: $$ t_{\text{min}} = \min \{ t \in \mathbb{N} \mid \forall k > t, \forall m \in \mathcal{M} : r(k)(m) = \emptyset \land S(k)(u)[1] = \emptyset \} $$ --- # Periodic Infinite Schedules (PIS) - Key concept in analysing non-termination in RAAF - Represents scenarios where flooding never terminates but enters a repeating cycle ---- ## Schedule Definition A schedule $\sigma$ is a function from natural numbers to configurations: $\sigma: \mathbb{N} \to \text{Configuration}$ Where $\sigma(j) = (S'_j, r_j)$ represents the configuration of the system in round $j$. - $S'_j$ is the augmented state function for round $j$ - $S'_j: V \to \left(\mathcal{P}(\mathcal{M}) \times (\mathcal{M} \to \mathcal{P}(V)) \times (\mathcal{M} \to \mathcal{P}(V)) \times (\mathcal{M} \cup \{\emptyset\})^{\text{CacheSize} + |\mathcal{M}|}\right)$ - $\pi: \mathbb{N} \to \left(V \to (\mathcal{M} \cup \{\emptyset\})^{\text{CacheSize} + |\mathcal{M}|}\right)$: priority permutation function. - Replaces the integer priority vector with a permutation over messages ordered by their priority - Allows us a finite state space - $r_j$ is the round function for round $j$ --- ## Definition of Periodic Infinite Schedules A schedule $\sigma$ is a periodic infinite schedule if there exist natural numbers $c$ (transient period) and $l$ (cycle length) such that: 1. $\forall j \geq c: \sigma(j) = \sigma(c + (j - c) \bmod l)$ 2. $\exists k \in \{0, 1, \ldots, l-1\}, \exists m \in \mathcal{M}: r_{c+k}(m) \neq \emptyset$ ---- ### Motivations - Guarantees non-zero asymptotic density of transmissions (i.e. no arbitrarily large delays between transmissions) - Strong enough to enable proofs about long-term system behavior, yet flexible enough to capture various adversarial strategies ---- ## PIS: Key Properties 1. Transient Period: Initial phase where behavior may be irregular 2. Cycle Structure: Finite sequence of configurations that repeats indefinitely 3. State and Transmission Repetition: Entire system configuration recurs cyclically 4. Persistent Activity: Guaranteed message transmission in each cycle --- ## PIS and Non-terminating Strategies - Theorem: Any graph admitting a non-terminating strategy also admits a PIS - Constructing PIS from non-terminating strategy: 1. Enumerate all possible configurations (finite set) 2. In any infinite schedule, some configuration must repeat 3. 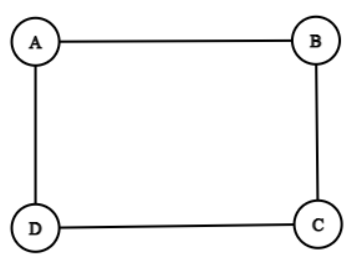Use the period between first and second occurrence of repeated configuration as cycle length ---- ## Significance - Foundation for all our non-terminating strategies - If a graph doesn't admit PIS, flooding must terminate - Simplifies proofs of non-termination --- ## Worked Example: PIS on a 4-Node Cycle Consider a graph $G$ with 4 nodes: $A$ (source), $B$, $C$, and $D$. Edges: $(A,B)$, $(B,C)$, $(C,D)$, and $(D,A)$. Message set: $\mathcal{M} = \{m_0\}$  ---- ### Adversary Strategy Delay function $d : G \to (\mathbb{N} \times V \times E \to \{0, 1\})$: $$ d(G)(i, u, e) = \begin{cases} 1 & \text{if } i \text{ is odd and } e \in \{(B,C), (D,A)\} \\ 1 & \text{if } i \text{ is even and } e \in \{(A,B), (C,D)\} \\ 0 & \text{otherwise} \end{cases} $$ --- ### State Description: First 6 Rounds <img src="https://i.imgur.com/wDp3hQz.png" width="500"> ---- <img src="https://i.imgur.com/io7LocK.png" width="500"> ---- <img src="https://i.imgur.com/FCP2Tku.png" width="500"> ---- <img src="https://i.imgur.com/fEo5PDF.png" width="500"> ---- <img src="https://i.imgur.com/FnjJgGd.png" width="500"> ---- <img src="https://i.imgur.com/CCzXDMx.png" width="500"> --- ### Key Observations - $S(1)(v) = S(5)(v)$ for all $v \in V$ - $r(1) = r(5)$ - The system enters a cycle of length 4 starting from round 1 --- ## Proof of Non-Termination 1. Define state function $S(i)$ and round function $r(i)$ for each round $i$ 2. Observe that $S(1)(v) = S(5)(v)$ for all $v \in V$ and $r(1) = r(5)$ 3. Prove by induction that for all $k \geq 1$ and all $v \in V$: $S(k)(v) = S(k+4)(v)$ and $r(k) = r(k+4)$ ---- ### Conclusion - System enters a perpetual cycle of length 4 - Satisfies PIS definition with $c = 1$ and $l = 4$ - Flooding process never terminates ---- This example demonstrates how a simple adversarial strategy can create a periodic infinite schedule, ensuring non-termination of the flooding process. The non terminating strategy on the 4-node line graph under the amnesiac destinations model can also be seen as an example of a periodic infinite schedule. --- # Termination Guarantees for Acyclic Graphs --- ## Main Result **Theorem:** in a simple, connected acyclic graph $G$ with source node $g_0$ under the RAAF model, with unbounded but finite delays, the flooding process always terminates in a finite number of rounds. --- ## Proof Approach - Induction on the eccentricity $k = e(g_0)$ of the source node - Prove for all acyclic graphs (trees) with increasing eccentricity --- ## Base Cases 1. $k = 0$: Graph consists only of $g_0$ - Terminates immediately (no edges to send along) 2. $k = 1$: Star graph with $g_0$ at center - Terminates in $1 + \max_{v \in V_1} B_0(g_0, v)$ rounds - $B_0(g_0, v)$: finite delay for edge $\{g_0, v\}$ - $V_1$: set of nodes adjacent to $g_0$ --- ## Inductive Hypothesis Assume theorem holds for all trees with eccentricity $\leq m$ --- ## Inductive Step (1/2) Consider a tree $G$ with $e(g_0) = m + 1$ - Let $V_1 = \{v \in V : d(g_0, v) = 1\}$ be nodes adjacent to $g_0$ - For each $v \in V_1$, let $G_v$ be the subtree rooted at $v$ - Note: $e(v)$ in $G_v$ is at most $m$ for each $v \in V_1$ --- ## Inductive Step (2/2) - Message reaches each $v \in V_1$ in at most $1 + B_0(g_0, v)$ rounds - Let $T_v$ be the finite termination time for subtree $G_v$ - By inductive hypothesis, $T_v$ is finite for all $v \in V_1$ --- ## Recurrence Relation $$T(m + 1) \leq \max_{v \in V_1} (1 + B_0(g_0, v) + T_v)$$ Where: - $B_0(g_0, v)$: finite (but unbounded) delay for edge $\{g_0, v\}$ - $T_v$: finite termination time for subtree $G_v$ --- ## Proof Conclusion The recurrence relation is finite because: - $B_0(g_0, v)$ is finite for all $v \in V_1$ - $T_v$ is finite for all $v \in V_1$ by induction - $V_1$ is a finite set - The maximum of a finite set of finite numbers is finite --- ## Significance - Shows robustness of termination in acyclic graphs - Contrasts with cyclic graphs, which can admit non-terminating strategies - Provides foundation for understanding RAAF behavior in more complex network topologies --- # Non-Termination Guarantees for Cyclic Graphs --- ## Main Result **Theorem:** for any simple, connected graph containing a cycle, there exists an adversarial strategy that prevents termination of the flooding process in the RAAF model. --- ## Proof Approach 1. Isolate a single cycle within the graph 2. Define an adversarial strategy for this cycle 3. Prove that this strategy leads to non-termination 4. Show that interactions with non-cycle nodes don't disrupt the cyclic flow --- ## Graph Setup - Let $G = (V, E)$ be a finite, simple, connected graph containing a cycle - $C = (V_C, E_C)$ is a cycle in $G$ where: - $V_C = \{v_1, v_2, \ldots, v_n\} \subseteq V$ - $E_C = \{\{v_i, v_{i+1 \bmod n}\} | 1 \leq i \leq n\} \subseteq E$ - $V_O = V \setminus V_C$ (nodes not in the cycle) - Single message $\mathcal{M} = \{m_0\}$ --- ## Adversarial Strategy For edges $\{v_i, v_{i+1 \bmod n}\} \in E_C$ and rounds $j > c$: $$ d(G)(j, v_i, \{v_i, v_{i+1 \bmod n}\}) = \begin{cases} 0 & \text{if } j - c \equiv i \pmod{n} \\ 1 & \text{otherwise} \end{cases} $$ For all other edges $e \in E \setminus E_C$: $$d(G)(j, u, e) = 0 \text{ for all } j \in \mathbb{N}, u \in V$$ We delay only the cycle interactions. --- ## Key Components of the Proof 1. Persistence of Destination Maps (PDM) 2. Cyclic Propagation 3. Non-Disruption by Non-Cycle Interactions --- ## 1. Persistence of Destination Maps (PDM) **Lemma:** if a node intends to send to its next cycle neighbor, it will continue to do so until successful transmission. Key idea: - If transmission is delayed, the destination remains in the node's destination map - If the message is overwritten in the cache then the destinations would also be present in the new destination map - Ensures the message keeps trying to move forward in the cycle --- ## 2. Cyclic Propagation Theorem: For all $i \in \mathbb{Z}^+$, in round $c + (i \bmod n)$, $v_{i \bmod n}$ transmits the message to $v_{(i+1) \bmod n}$. Proof sketch: - Base case: Show it holds for $i = 1$ (obtains by definition of delay function) - Inductive step: Prove for $i + 1$ assuming it holds for $i$ (implied by flooding rules) - Use PDM lemma to ensure message propagation --- ## 3. Non-Disruption by Non-Cycle Interactions Show that interactions with $V_O$ don't affect the cyclic flow: 1. Sending to non-cycle nodes: - Doesn't prevent transmission within the cycle 2. Receiving from non-cycle nodes: - Either doesn't affect cycle transmission - Or reinforces the cycle flow --- ## Proof Conclusion - The adversarial strategy ensures a message transmission within the cycle every $n$ rounds - This creates a Periodic Infinite Schedule[^PIS] with: - Transient period $c$ - Cycle length $n$ - Therefore, flooding never terminates on the graph [^PIS]: Specifically, the behaviour of $V_C$ forms a periodic infinite schedule if you ignore non-cycle interactions (viable because we show that non-cycle interactions do not disrupt cyclic flow). --- ## Significance - Shows that cycles are sufficient for non-termination - Contrasts with guaranteed termination in acyclic graphs - Highlights the impact of graph structure on flooding behavior --- # Undecidability of Flooding Termination for Cyclic Graphs --- ## Main Result **Theorem:** the flooding termination problem is undecidable for the RAAF model with an oblivious adversary, given that the adversary is an arbitrary computable function. --- ## Proof Approach 1. Reduce the halting problem for Turing Machines to the flooding termination problem 2. Construct a simple graph and a delay function that simulates a Turing Machine 3. 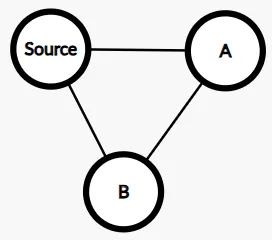Show that flooding terminates if and only if the Turing Machine halts --- ## Graph Construction - 3-node cycle graph: $G = (V, E)$ - $V = \{\text{Source}, A, B\}$ - $E = \{\{\text{Source}, A\}, \{A, B\}, \{B, \text{Source}\}\}$  --- ## Delay Function Constructor ```python def constructDelayFunction(TM, x): def delay(round, node, edge): TM_state = simulateTM(TM, x, round) if TM_state.isHalted: return False # No delays, allowing termination else: return defaultNonTerminatingStrategy(round, node, edge) return delay def defaultNonTerminatingStrategy(round, node, edge): if round % 3 == 0: return edge == {Source, B} elif round % 3 == 1: return edge == {Source, A} elif round % 3 == 2: return edge == {A, B} ``` --- ## Key Ideas of the Proof 1. The delay function simulates a Turing Machine (TM) for progressively longer durations 2. If TM halts, delays stop, allowing flooding to terminate 3. If TM doesn't halt, a non-terminating cycle is maintained 4. The default strategy ensures non-termination unless explicitly stopped --- ## Non-terminating Strategy Visualization <img src="https://i.postimg.cc/wvWsVSfs/S-0.png" width="500"> ---- <img src="https://i.postimg.cc/s1d4Rkp0/S-1.png" width="500"> ---- <img src="https://i.postimg.cc/RhnLySnH/S-2.png" width="500"> ---- <img src="https://i.postimg.cc/RC6r4w7c/S-3.png" width="500"> ---- <img src="https://i.postimg.cc/ZRQLwB0m/S-4.png" width="500"> ---- <img src="https://i.postimg.cc/59Zh0jgD/S-5.png" width="500"> ---- <img src="https://i.postimg.cc/vZyCrjpz/S-6.png" width="500"> ---- <img src="https://i.postimg.cc/X7dTy3Dq/S-7.png" width="500"> ---- <img src="https://i.postimg.cc/cLc2XhWN/S-8.png" width="500"> ---- <img src="https://i.postimg.cc/N0fVVXG2/S-9.png" width="500"> ---- * Observe that $S_3 = S_9$. * The default nonterminating strategy provided forms a periodic infinite schedule --- ## Proof Sketch 1. If TM halts on input $x$: - Delays stop after finite number of rounds - Flooding terminates within $3$ rounds of delays stopping 2. If flooding terminates: - Delays must have stopped - TM must have halted within finite number of steps Therefore, deciding flooding termination would solve the halting problem. --- ## Implications - Termination is undecidable for any cyclic graph in the RAAF model given a (computationally) powerful adversary - Highlights the significant impact of adversary's power on analysability - Motivates the need for restricted adversary models --- # Periodic Finite State Adversary (PFSA) --- ## Motivation - Bridge the gap between undecidability and practical analysis - Represent meaningful restrictions on adversary's power - Model real-world periodic network disruptions --- ## PFSA Definition Let $A = (Q, \Sigma, \delta, q_0, F)$ be a deterministic finite automaton where: - $Q$: finite set of states - $\Sigma = V \times E \times \{0, 1, \ldots, k-1\}$: input alphabet - $\delta: Q \times \Sigma \rightarrow Q$: transition function - $q_0 \in Q$: initial state - $F \subseteq Q$: set of accepting states Delay function: $$ d(G)(i, u, e) = \begin{cases} 1 & \text{if } \delta^*(q_0, (u, e, i \bmod k)) \in F \\ 0 & \text{otherwise} \end{cases} $$ --- ## Key Properties - Finite state behavior - Periodic with respect to round numbers - Adjustable memory via parameter $k$ - Balances expressiveness and analysability --- ## Decidability Result **Theorem:** the termination problem for RAAF with a PFSA is decidable. --- ## Decision Procedure Outline 1. Enumerate all possible states of the RAAF system 2. Simulate the system step by step from the initial state 3. For each step: - If all destination maps are empty, terminate - If a previously seen state is reached, declare non-termination (as the system then enters an endless cycle) - Otherwise, continue to the next step 4. Simulation halts due to finite state space --- ## Time Complexity - Worst-case time complexity: $$O(2^{2|V|^2 + 2|E| + \epsilon})$$ - Derived from the number of possible states: - Graph configurations (messages): $O(2^{2|V|^2})$ - Graph configurations (delays): $O(2^{2|E|})$ - PFSA periods: $O(k)$ --- # Conclusions and Future Work --- ## Summary of Main Contributions 1. Formal RAAF model - Precise protocol description - Enables rigorous proofs 2. Termination analysis - Proved termination for acyclic graphs - Demonstrated non-termination for cyclic graphs 3. Decidability results - Undecidability for arbitrary computable adversaries - Decidability for Periodic Finite State Adversary (PFSA) --- ## Potential Applications - Resource-constrained IoT networks - Memory-efficient flooding protocols - Distributed systems with unreliable communication - Understanding behavior under adversarial conditions - Network topology analysis - Leveraging termination properties to infer graph structure --- ## Open Questions - Complexity of deciding termination in PFSA model - Currently only shown to be decidable - Exact complexity class unknown, suspected to be rather hard --- ## Future Research Directions 1. Other restrictions on adversary's computing power - Explore models between PFSA and arbitrary computable functions 2. Extend results to multi-source/multi-message settings - Analyse interactions between multiple flooding processes 3. Probabilistic analysis of RAAF - Introduce randomised delays or message losses 4. Dynamic graph structures - Study RAAF behavior in temporal graphs --- ## Conclusion - RAAF model provides insights into flooding behavior under adversarial conditions - Results highlight the impact of graph structure and adversary power on termination - Future work can further bridge theory and practical applications in distributed systems --- # References [1] W. Hussak and A. Trehan, "On The Termination of a Flooding Process," arXiv:1907.07078v1 [cs.DS], Jul. 2019. [Online]. Available: https://arxiv.org/abs/1907.07078