# 2021~2023 TOI 初選
TOI 沒有保證題目會照難度排
## 2023 TOI 初選
### [A. 房屋推薦 (house)](https://zerojudge.tw/ShowProblem?problemid=k184)
座標平面上有$n$個房子，$m$個捷運站
1. 房屋與最近的捷運站的距離越短越好。
2. 如果兩間房屋和彼此最近的捷運站距離一樣近，月租金越小的房屋越好。
3. 如果兩間房屋和彼此最近的捷運站距離一樣近，而且月租金相同，房屋編號越小的越好。

開發一個房屋推薦系統，對房屋們進行排序。
* $1\leq n\leq 10^5$
* $1\leq m\leq 10^3$
:::spoiler 解法:
對於每間房子找與最近的捷運站的距離，然後直接排序就好了

sort(houses.begin(),houses.end(),[](auto i,auto j){
    if(i.dis!=j.dis) return i.dis<j.dis;
    if(i.rent!=j.rent) return i.rent<j.rent;
    return i.num<j.num;
})

:::

### [B. 裁員風暴 (storm)](https://zerojudge.tw/ShowProblem?problemid=k185)
有$n$個項目，每個項目都有權重，從中選擇兩個項目(可重複)
問所有選擇中平均第$k$大的為多少?
* $1\leq n\leq 2\times 10^5$
:::spoiler 解法:
* 對答案二分搜
* 找最後一個$x$，使得大於等於$x$的選擇為k種
* 要查大於等於$x$的選擇有幾種，把權重排序後用雙指標計算對於每一個數字往左有多少個數字可以和他配
* 最後算出答案後要再記得除2
:::
:::spoiler code:

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,k;
vector<int> w;
int check(int x){
    int ret=0;
    int l=0,r=n-1;
    while(r>=l){
        while(r>=l&&w[r]+w[l]<x) l++;
        if(r<l) break;
        ret+=r-l+1;
        r--;
    }
    return ret;
}
signed main(){
    cin>>n>>k;
    w.resize(n);
    for(int i=0;i<n;i++) cin>>w[i];
    sort(w.begin(),w.end());
    int l=-2e14-1,r=2e14+1;
    while(r>l+1){
        int mid=(l+r)>>1;
        if(check(mid)>=k) l=mid;
        else r=mid;
    }
    cout<<(l%2==0? l/2:l)<<endl<<(l%2==0? 1:2)<<endl;
    return 0;
}

:::
### [C. 關卡地圖 (game)](https://zerojudge.tw/ShowProblem?problemid=k186)
給一棵有點權(可能為負)的樹或多一條邊的樹，問所有路徑中總權最大為何?
* $1\leq n\leq 10^5$
:::spoiler 樹解法:
每個點紀錄兩個值:
* `dp[i]`:以`i`為根的子樹的答案
* `down[i]`:從`i`往下延伸能得到的最大總權
令`v[i]`為`i`的所有子節點
若路徑有通過`i`，`dp[i]為w[i]`+子節點中最大的兩個(或一個或沒有)down值之和

void dfs(int pre,int pos){
    int a=0,b=0;
    down[pos]=w[pos];
    for(int i:v[pos]){
        if(i==pre) continue;
        dfs(pos,i);
        down[pos]=max(down[pos],down[i]+w[pos]);
        if(a<b) swap(a,b);
        b=max(b,down[i]);
        dp[pos]=max(dp[pos],dp[i]);
    }
    dp[pos]=max(dp[pos],a+b+w[pos]);
}

:::
:::spoiler 水母圖解法:
多一條邊的樹會恰好有一個環，有兩種情況:
* 路徑沒有通過環: 答案為環上的每一個點分別往下算的dp最大值
* 路徑有通過環: 答案為環上兩個節點的down值+兩節點間的點權和

對於第二點，把環攤開後有兩種情況:
* 路徑完整地在陣列內:
維護一個`set s`和一個`int a`(紀錄目前鍊上的總和)，對於每個點`i`，以`i`為右的答案為`*s.rbegin()+a+down[i]`，算完後把`down[i]-w[i]-a`丟進`s`內，並更新`a`值。
s={} a=0 ans[0]=0
s={7} a=4 ans[1]=20
s={-1,7} a=10 ans[2]=32
s={-1,2,7} a=13 ans[3]=22
* 最前面的一段+最後面的一段:
維護`l[i]`、`r[i]`:每個點往前(或後)最大的 **前綴的鍊的和+停止的地方的(down-w)**
答案即為所有的`l[i]+r[i+1]`的最大值
:::
## 2022 TOI 初選
### [A. 迷宮入口(entrance)](https://zerojudge.tw/ShowProblem?problemid=h557)
在2維座標平面上，有$n$個圖騰，你可以在平面上選任意的一個格子點，以你在的座標半徑為$r$畫圓，請問有多少個格子點可以覆蓋奇數個圖騰?
* $n\leq 2500$
* $1\leq r\leq 10$
* $|x_i|\leq 10^6$
* $|y_i|\leq 10^6$
:::spoiler 解法:
以每個圖騰為中心，半徑為r畫圓，搭配`map<pair<int,int>,int>`，計算每個點能覆蓋到多少圖騰

for(auto t:totem){
    for(int i=t.x-r;i<=t.x+r;i++){
        for(int j=t.y-r;j<=t.y+r;j++){
            if((i-t.x)*(i-t.x)+(i-t.y)*(i-t.y)<=r*r) m[{i,j}]++;
        }
    }
}

:::
### [B. 打鍵盤(keyboard)](https://zerojudge.tw/ShowProblem?problemid=h558)
給字串s，問雙手在鍵盤上的最小總移動距離。一開始左、右手食指分別在F與J的位置。 每次可以選擇一隻手指往按鍵的旁邊六個相鄰按鍵移動
* $n\leq 10000$
:::spoiler 解法:
令`dp[i][j]`為打完前`i`個字母，一隻手在`j`，另一隻手在`s[i]`的最小總移動距離

dp[i+1][j]=max(dp[i+1][j],dp[i][j]+dis(s[i],s[i+1]);
//手從s[i]、j移動到s[i+1]、j
dp[i+1][s[i]]=max(dp[i+1][s[i]],dp[i][j]+dis(j,s[i+1]));
//手從s[i]、j移動到s[i]、s[i+1]

:::
### [C. 共享自行車 (bike)](https://zerojudge.tw/ShowProblem?problemid=h559)
給一棵$n$個點的帶邊權的樹，總共有$n\times k$個腳踏車分布在點上，問搬運腳踏車使每個點恰有$k$輛腳踏車的最小總距離為和?
:::spoiler 解法:
DFS時算該節點底下的每個子節點分別共有多少台需要往下(或往上)搬，再乘上邊的邊權即為這條邊對答案的貢獻。

void dfs(int pre,int pos){
    sum[pos]=1;//子樹節點數量
    bikes[pos]=bike[pos];//子樹腳踏車總數
    for(edge i:v[pos]){
        if(i.num==pre) continue;
        dfs(pos,i.num);
        sum[pos]+=sum[i.num];
        bikes[pos]+=bikes[i.num];
        ans+=abs(bikes[i.num]-sum[i.num]*k)*i.w;
    }
}

:::
## 2021 TOI 初選
### [A. 原始人排序](https://tioj.ck.tp.edu.tw/problems/2193)
將$n$個十進位表示的數字依二進位表示法中$1$的個數由小而大排序，若兩數字的二進位表示中$1$的個數相同，則依輸入時的順序輸出。
* $n\leq 10^3$
* $1\leq a_i \leq 2^10$
::: spoiler 解法:

stable_sort(v.begin(),v.end(),[](int x,int y){
    return __builtin_popcount(x)<__builtin_popcount(y);
});

`stable_sort`為當兩數字一樣時，不會變更原本的數字的排序
`__builtin_popcount()`為二進位表示法中$1$的個數
:::
### [B. 掃地機器人](https://tioj.ck.tp.edu.tw/problems/2194)
今有$n$間位於同一走廊的教室需要打掃，這些教室由左而右分別編號為$1$至$n$，每間教室的髒亂程度各有不同。假設機器人在同一間教室必須打掃整數分鐘的時間，並且每分鐘能吸除的灰塵量會隨時間線性遞減，減至$0$則不會再減少。在$m$分鐘內可掃除的最大灰塵量?
* $n\leq 1000$
* $m\leq 10^9$
### [C. 粉刷護欄](https://tioj.ck.tp.edu.tw/problems/2195)
有兩條水平木樑，上面各有$n$個點。另有$n$條護欄，各有編號並連接兩條木樑。問最多可選擇幾條護欄互不交錯，輸出一組字典序最大的解。
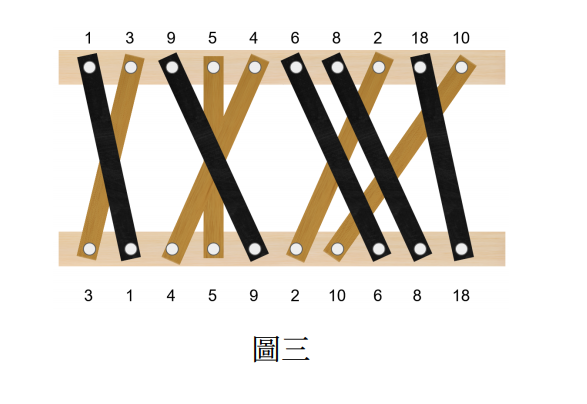
此圖答案為 3 9 6 8 18
* $n\leq 2\times 10^5$

## 參考資料
https://www.twpca.org/