## Introduction

This work aims to explore and advance Private Proof Delegation (PPD) using the FHE-SNARK paradigm, where a server homomorphically generates a zk-SNARK over an encrypted client witness.

In the [previous document](https://hackmd.io/@timofey/r1FuxwVsJg), we compared FHE-SNARK with other PPD techniques and proposed several research [directions](https://hackmd.io/@timofey/r1FuxwVsJg#Future-work) to improve performance, practicality, and security.

Here, we focus on laying the groundwork for a practical end-to-end prototype. We analyze and specify key components: FHE-friendly IOPs, PCS for encrypted values, and an efficient Proof of Decryption (PoD) mechanism for public verifiability. We propose concrete improvements to these components and outline implementation path.

We have developed the prototype, [ChainSafe/delegated-fhe-ligero](https://github.com/ChainSafe/delegated-fhe-ligero), and benchmarked it against alternative approaches such as CoSNARKs and Delegated Spartan to confirm feasibility. Beyond that, future work will include formalizing security guarantees and incorporating lookup arguments in FHE-SNARKs.

## Related works

### [HELIOPOLIS](https://eprint.iacr.org/2023/1949)

Introduced a technique termed HE-IOP, adapting interactive oracle proofs (IOPs) to operate over homomorphically encrypted data. It transforms plaintext oracle queries of the verifier into ciphertext oracles, allowing the prover to perform computations homomorphically without seeing plaintexts.

HELIOPOLIS _only_ implements the HE-FRI protocol, optimizing it for homomorphic computation by _reducing multiplicative depth through specialized linear-algebraic methods, such as shallow-folding and optimized NTT algorithms using SIMD packing_. As a result, homomorphic evaluation of FRI commit phase with codewords up to $2^{11}$ degree takes 5.4s (32-core) using 4GB RAM.

### [Blind SNARKs](https://eprint.iacr.org/2024/1684)

A full FHE-SNARK construction for proving the Fractal SNARK (R1CS+FRI) inside GBFV homomorphic encryption scheme. It replaces prover oracles with encrypted representations: witness $z$ is encoded as a univariate encrypted polynomial $\tilde{z}$ such that $\tilde{z}\left(h_i\right)=z_i$ for a specific set $H=\left\{h_0, \cdots, h_{n-1}\right\}$. Vectors $A z, B z$, and $C z$ are encoded similarly. Verifying $A z \circ B z=C z$ ultimately reduces to checking, via FRI protocol homomorphically.

The chosen FHE parameters, particularly the cyclotomic polynomial $\Phi_m(X)$ and the plaintext modulus $t(X)$, are selected such that the plaintext space of the GBFV scheme becomes _isomorphic to a vector space of dimension 384 over the field extension_ $\mathbb{F}_{p^2}$, where $p$ is the Goldilocks prime, commonly used in SNARKs. This field extension is _especially suitable as it causes small noise growth_ in homomorphic operations. For a circuit size of $2^{20}$ R1CS constraints, the estimated sequential runtime is 9.26h, with 32-x parallelization this is reduced to 17.4m. This results in a 116MB proof size.

The proposed PoD construction for public verifiability of FHE-SNARK uses a vectorized version of the [LNP22](https://crypto.iacr.org/2022/papers/538804_1_En_3_Chapter_OnlinePDF.pdf) lattice-based sigma protocol to accommodate non-power-of-two cyclotomic parameters. This PoD prover has a $O(r n^2)$ complexity with $r$ being the number of decryptions, tied to the number of FRI queries for probabilistic soundness. A sufficiently large $r$ (e.g., $r > 2000$ for a $2^{20}$ constraint system) would lead to a proving runtime of hours. Using _modulus switching to reduce $n$ to a smaller dimension $n^{\prime}$ and batching many PoDs_, authors reduce it to ~2s (on 8-core CPU). The resulting proof size is 12KB.

Blind SNARKs and other HE-FRI constructions _require NTTs for Low-Degree Extension (LDE) and polynomial multiplications_, which are nonlinear and expensive to compute homomorphically. Despite optimizations like 2-layer NTT, _these schemes suffer from high noise accumulation due to large multiplicative depth._

### [Practical FHE-SNARK for VC](https://eprint.iacr.org/2025/302)

Unlike prior constructions, this latest FHE-SNARK scheme builds upon the “multilinear PCS + polynomial interactive oracle proof (PIOP)” paradigm. Namely, it allows for homomorphic proving of the Spartan PIOP + Ligero/Breakdown based PCS, referred to as an FHE-friendly SNARK. This construction is optimized for packed homomorphic operations, making it best suited for second-generation FHE schemes like BFV or BGV.

Here, witness $z$ and vectors $A z, B z$, and $C z$ are encoded as encrypted multilinear polynomials; verifying $A z \circ B z=C z$ involves a multivariate zero-check, reduced to a sumcheck avoiding NTT unlike univariate FRI-based approaches. To avoid significant multiplicative depth in running sumchecks homomorphically, each round evaluations are batch and computed as linear combinations. For arithmetic circuits with $2^{20}$ gates, their implementation takes 3.6 hours (12.3 ms/gate) to generate a computation proof on a single-core CPU. This results in a 65MB proof size with 2.7s verification (single core).

Zhang et al. establish that FHE-SNARK fits the VC (Verifiable Computation) security model and show an input-dependent attack when the _server, supposed to have a private witness, crafts its input based on the client’s encrypted input_, leading to incorrect/manipulated results without violating traditional soundness. To address this, they enforce knowledge soundness by requiring the server to “know” (commit) their private inputs.

In FHE-SNARK, the witness can be partially encrypted (the client’s private inputs), a novel _polynomial commitment scheme for hybrid values_ (some evaluations encrypted, others plaintext) is devised so the plaintext portion of the witness can be “extracted” (opened) without the FHE secret key. The _multilinear structure allows us to organize these hybrid evaluations on a hypercube in a structured manner_, referred to as the “cryptomix” representation.

This work focuses on general verifiable computation and doesn’t provide a PoD scheme for PPD public verifiability. Furthermore, it overlooks the significance of lookup arguments in modern VC applications and fails to provide an FHE-friendly lookup PIOP.

Also see [**related works re. FHE-SNARK security.**](https://hackmd.io/@timofey/ryYXSoIC1g#Related-works)

## Components

### FHE-friendly IOP

In FHE, the name of the game is minimizing multiplicative depth. Accordingly, the preference for R1CS-based IOPs over PLONK or AIR stems from their inherent linearity and lower multiplicative depth.

- **Fractal (holographic) IOP** used in Blind SNARK follows a standard R1CS structure, reducing to linear matrix-vector operations (i.e., checking $Az \circ Bz = Cz$) and the final product check.
An IOP is holographic (hIOP) if it can be separated into public (witness-independent) and private (witness-dependent) parts. This structure **allows expensive witness-independent computations to be done in clear, reducing the FHE overhead.**
Fractal archives holography via an indexer that preprocesses a circuit, enabling the verifier to query a circuit encoding using only an index, without a full circuit description.
- **Spartan PIOP** used in FHE-SNARK operates over multilinear polynomials and is reduced to the sumcheck protocol. It’s holographic, featuring witness-independent computation commitments to R1CS relation $\tilde{A}, \tilde{B}, \tilde{C}$ MLEs and Sparse PCS to prove consistency with committed witness via witness $\tilde{z}$.
**The advantage is that multilinear polynomial evaluation is linear, avoiding FFT/NTT; while the sumcheck instances can be batched via RLC, amortizing multiplicative depth in FHE.** This enables efficient FHE-friendly proving directly over encrypted data without preprocessing.

Additionally, the R1CS structure allows flexibility to freely order the variables in the vector $z = (x, w)$. The matrices $A, B, C$ define how these variables interact to satisfy the constraints, where $z=(x, w)$ is the concatenated statement and witness vector. This vector can be permuted arbitrarily (e.g., $z^{\prime}=T z$) without altering the R1CS relation:$$
\left(A T^{-1} \cdot z^{\prime}\right) \circ\left(B T^{-1} \cdot z^{\prime}\right)=C T^{-1} \cdot z^{\prime}\tag{1}
$$ This flexibility enables grouping elements in $z^{\prime}$ so plaintext elements are in the top rows of a matrix and ciphertexts in the lower rows, supporting plaintext/ciphertext separability in PCS for hybrid values discussed later.

#### Comparison with AIR & PLONK

| | **PLONK** | **AIR** | **R1CS** |
|----------------------------|----------------------------------------------------------------------|------------------------------------------------------------------|---------------------------------------------------------------------------------------------|
| **Linearity** | Low — nonlinear gates, permutation checks | Moderate — transition constraints may be nonlinear | High — matrix-vector ops (Fractal) or multilinear sumchecks (Spartan) |
| **Multiplicative depth** | High — deep circuits for permutation and quotient checks | High — multiple polynomials for constraint and trace checks | Low — batched or shallow-depth linear algebra; sumcheck batching via RLC |
| **FFT/NTT cost** | High — for polynomial ops and basis transformation | High — use for trace LDE | Depends — Multilinear PIOP avoids FFT; else use for basis transformation |
| **SIMD/Ciphertext packing**| Poor — permutation checks | Likely good — according to Stwo | Good — flexibile witness ordering |

### PCS for encrypted values

The prover server claims knowledge of a multilinear polynomial $\tilde{f}$ that evaluates to a ciphertext $ct[a]$ (client’s witness) at some point $b \in \{0,1\}^n$ and satisfies some circuit relation reduced to a polynomial identity via the sumcheck protocol.

To prove this polynomial identity, the prover opens $ct[u] \leftarrow \tilde{f}(r)$ at some challenge point $r$ picked by the verifier. The designated verifier (a client with the secret key) can decrypt $ct[u]$ and check if it equals $u$ that satisfies polynomial identity.

We now define PCS on encrypted values for practical FHE-SNARK. Since [Zhang et al.](https://eprint.iacr.org/2025/302) didn’t specify public verifiability for their construction, we suggest a PoD extension inspired by Blind SNARKs.

Recall the standard Breakdown PCS scheme that FHE-SNARK builds on:

#### Setup
The client (designated verifier) picks secret key $sk \leftarrow \operatorname{\mathcal{E}.KeyGen}(1^{\lambda})$ and commits to it $C_{sk}$ and sends it to the server.

The server (remote prover) runs the Spartan PIOP setup algorithm $\mathcal{I}$ on input $\mathbb(\mathbb{F}, A, B, C)$ with R1CS matrices $A,B,C$ for circuit $\mathcal{C}$ over the prime field $\mathbb{F}$ and uses a (standard) Ligero PCS to instantiate the polynomial oracles. This outputs multilinear extension polynomials $\widetilde{A}, \widetilde{B}, \widetilde{C}$ as the prover key $pk$; and the verifier key $vk$ as commitments to these three polynomials.

#### Delegated proving
The client encrypts statement $x$ and witness $w$ into $(ct[x], ct[w]) \leftarrow\operatorname{\mathcal{E}.Enc}_{\mathrm{pk}}((x, w))$ and sends it to the server.

The server
1. Homomorphically computes the output of the circuit $ct[\text{out}] = \mathcal{E}.\operatorname{Eval}(\mathcal{C}, (ct[x], ct[w]))$ and constructs R1CS witness vector $z = (1, ct[x], ct[\text{out}], ct[w])$.
2. Pads $z$ to size $2^n$ and rewrites it as a $2^d \times 2^{n-d}$ matrix $M$, encodes row-wise into $\hat{M}$ and Merkle commits into $com$.
3. Runs Spartan PIOP to check standard R1CS relation via reduction to batched sumcheck and PCS evalcheck computed homomorphically.

This outputs the proof $\pi^{\text{dv}} = [ct[u], \{ct[\hat{v_j}], \text{ap}_j\}, com, \tau]$ where:
- $ct[u]$ is a row vector where each element is a linear combinations rows of $M$ with random scalars $\{r_i\}$ sampled from the transcript $\tau$, i.e., $ct[u_j] := \sum_{i \in[2^d]} r_i \cdot M[i,j]$
- $ct[\hat{v_j}]$ is a claimed column vector of the encoded matrix $\hat{M}$ for each queried column $\{j \subseteq [0, 2^d-1]\}_{j\in O(\lambda)}$
- $\text{ap}_j$ is an authentication path connecting a claimed column $[\hat{v_j}]$ to the PCS commitment $com$, Merkle-hash of all columns in $\hat{M}$.

#### PoD

1. Compute linear combination (for [bathing PoDs](#Batching-query-PoDs)) of all relevant ciphertexts $\vec{ct} = \{ct[u_i]\} | \{ct[\hat{v}_j]\}$ with random plaintext scalars $\{\alpha_i\}$ sampled from the transcript $\tau$ $$
ct^\prime = \sum_{i\in{2^d+O(\lambda)}} \operatorname{ptMult}(ct_i, \alpha_i)
$$
2. Decrypt $\vec{ct}$ into $\vec{pt}$ and compute linear combination of plaintexts with $\{\alpha_i\}$.
3. Prove using secret key $sk$ and its commitment $C_{sk}$ verifiably decrypts $ct^\prime$ into $pt^\prime$: $$
\begin{align}
pt^\prime &= \sum_{i \in{2^d+O(\lambda)}} \alpha_i \cdot pt_i
\\
\pi^{\mathrm{PoD}} &\leftarrow \operatorname{PoD.P}(\mathrm{C}_{sk}, ct^\prime, pt^\prime)
\end{align}
$$
The final public proof $\pi^{\text{pv}} =[\pi^{\mathrm{PoD}}, \{ct[u_i],u_i\}, \{ct[\hat{v_j}], \hat{v_j}, \text{ap}_j\}, ct[x], com, \tau]$

#### Public verifier
1. Compute linear combinations of random plaintext scalars $\{\alpha_i\}$ sampled from the transcript $\tau$ with ciphertexts $\vec{ct} = \{ct[u_i]\} | \{ct[\hat{v}_j]\}$ and plaintexts $\vec{pt}=\{u_i\}|\{\hat{v}_j\}$; accept if $\text{acc} \stackrel{?}{=} \operatorname{PoD.V}(\pi^{\mathrm{PoD}}, \mathrm{C}_{sk}, ct^\prime, pt^\prime)$.
2. Verify that all authentication paths $\{\text{ap}_j\}$ are valid with respect to $com$.
3. Encode $\hat{u} = \operatorname{Enc}({u})$ with the same code used to encode matrix $M$.
4. Recover vector $\{r_i\}$ from the transcript $\tau$ and for each queried column $j\in O(\lambda)$ check that the inner product $\langle r,\hat{v}_j\rangle$ equals the $j$-th element of the encoded vector $\hat{u}$.
5. Run verifier Spartan PIOP (zerocheck) to get an evaluation point $\beta$, check PCS evaluation phase to verify that $f(\beta)$ evaluates to claimed value.

### Alternative choice of PCS

#### Blaze

[Blaze](https://eprint.iacr.org/2024/1609) has linear commitment and prover time, and $O(\lambda \log^2 n)$ verifier time and evaluation proof size, achieved by combining a Brakedown-style PCS with Basefold. It eliminates FFT/NTT overhead for encoding by interleaving (row-wise encoding from Brakedown). The commitment phase is identical to Brakedown (also Ligero, and Binius), except for the error-correcting code—RAA code in Blaze, defined only for binary fields (characteristic 2; GF2).

_How well can a SNARK over GF2 be proved homomorphically, as an FHE-SNARK?_

- It depends on the FHE scheme—leveled schemes (BFV/BFV) often [lack bit arithmetic support](https://crypto.stackexchange.com/a/83833) due to a non-power-of-two polynomial degree, breaking NTT optimizations. Conversely, gate-based schemes (FHEW/TFHE) can efficiently evaluate boolean gates (e.g., NAND, XOR, AND) directly by encrypting one bit per ciphertext and bootstrapping. **The tradeoff is poor ciphertext packing and SIMD support in FHEW/TFHE, crucial in existing FHE-SNARK constructions.**
- Bit operations support is insufficient; SNARK soundness requires large binary field extensions (GF128). BGV/BFV [can support](https://arxiv.org/pdf/2101.07078#:~:text=For%20example%2C%20while%20we%20generally,46) such extensions. The downside is that **implementing circuits in GF(2^d) boils down to bit operations (grouped), and ensure no overflow beyond the field.**

For the evaluation proof, Blaze employs FRI-Binius (BaseFold extension for binary fields) to reduce proof size. Instead of using the multilinear extension of the interleaved RAA code, Blaze sends Reed-Solomon encodings of intermediate stages in the RAA encoding, and uses BaseFold-FRI to "pretend" it has access to the multilinear extension of these values.

The Blaze verifier is amenable to Blind SNARK PoD techniques, involving a batched sumcheck and FRI queries that can be verifiably batch decrypted via linear combination. However, the proving routine runs a batched sumcheck and [**permutation check**](https://eprint.iacr.org/2024/1609.pdf#page=29) **which translate to expensive ciphertext slot swaps.**

#### BrakingBase

[BrakingBase](https://eprint.iacr.org/2024/1825) combines techniques from Brakedown and BaseFold, achieving linear prover time and $O(\lambda \log^2 n)$ verifier time. Unlike Blaze, BrakingBase is field agnostic and designed for Spartan PIOP.

The commitment is identical to Brakedown except the dimensions of matrix logarithmic in the size $n$ of the committed vector, i.e., the prover encodes $\frac{n}{O(\log n)}$ rows. This **reduces the client’s PoD (computing linear combinations) work to logarithmic**, although only for $ct[u]$ since $ct[\hat{v}]$ depends on security parameter $\lambda$. The code can be any linear error-correcting code e.g., Spielman’s code suggested by Brakedown which is field-agnostic—**binary fields aren’t required.**

The evaluation employs proof composition for poly-logarithmic verifier time and proof-complexity. Instead of sending the intermediate vector $p$ (as in Breakdown's proximity test), the BrakingBase prover sends a commitment to $(p, p^\prime)$ using the Basefold PCS (RS.encode + Merkle proof), where $p^\prime$ is such that $(p,p^\prime)=\operatorname{Enc}(p)$. The verifier uses a batched sum-check protocol to validate the claims—**no permutation is involved.** Although extra commitment and sumcheck increase prover workload, evaluation remains linear in the size of the input polynomial's coefficient vector. Concretely, Breakdown evaluation prover remains most efficient; **with BrakingBase we trade some extra linear prover work for polylogarithmic public verifier and PoD client prover.** *These benefits would be more pronounced if [WHIR](https://eprint.iacr.org/2024/1586.pdf) is used instead of BaseFold.*

### Lattice-based PCS

Lattice-based PCS are often built on the same arithmetic structure and hardness assumptions as FHE, making them an attractive option for homomorphic proving and on-client PoD generation.

Based on the previous discussion, here are some desired structural properties:

- [Ciphertext packing](#PCS-for-packed-ciphertexts)—whether expensive computations, like NTTs, are structurally amenable to SIMD parallelization.
- [Modulus alignment](https://hackmd.io/L-XVj9_rQIeU6OMpB_rxCA?view=&stext=1306%3A334%3A0%3A1744384413%3Az_zyCt)—FHE plaintext space is isomorphic to PCS internal modulus.
- [Low non-linear overhead](https://hackmd.io/L-XVj9_rQIeU6OMpB_rxCA?view=&stext=2733%3A276%3A0%3A1744384724%3Aqogga8)—limited use of NTTs, approximate, bitwise arithmetic.
- (Ideally) [multilinear support](https://hackmd.io/L-XVj9_rQIeU6OMpB_rxCA?view=&stext=6487%3A188%3A0%3A1744384756%3AqZrx-J)—can commit and evaluate multilinear polynomials (w.r.t Spartan PIOP).

#### Common challenges with FHE-compatibility

- Many lattice-based PCS are multi-round and interactive, necessitating the Fiat–Shamir transform. Hashing inside FHE is expensive, so challenges must be externally injected. Although security implications of such injection are out of this document’s scope, we note that this is a sensitive area for security analysis.
- Blinding and zero-knowledge often rely on discrete Gaussian or rejection sampling (approximate arithmetic / branching heavy)—doing this homomorphically adds noise and circuit depth unless external randomness is injected. Many protocols depend on NTT for efficient polynomial arithmetic, introducing significant noise growth.
- Other components causing multiplicative depth growth are norm-checks (extensive squaring), deep folding recursion (lots of linear combinations), and sequential sum-check rounds (usually amortized via batching). Some schemes rely on structured randomness or bit-level operations, which are FHE-unfriendly.

We analyzed many lattice-based PCS for FHE compatibility. Despite algebraic alignment, most schemes aren’t ideal for homomorphic proving: Greyhound and SLAP rely heavily on NTTs and deep recursive folding. Greyhound also embeds LaBRADOR SNARK, adding further complexity. [Cini et al.](https://eprint.iacr.org/2018/560.pdf) use Stern protocols with bit-level operations; LaBRADOR and ABDLOP rely on trapdoors and structured noise sampling.

#### [LatticeFold](https://eprint.iacr.org/2024/257)

A lattice-based folding SNARK built over Ajtai commitments, with recursive witness folding via random linear combinations. The sum-check folding verifier enforces short folded witnesses to preserve SIS soundness. Authors emphasize the protocol operates over the same module structure as FHE, using $R_q = \mathbb{Z}_q[X]/(X^n + 1)$ with $q \approx 2^{64}$—enabling direct FHE plaintext alignment.

_Downsides:_ LatticeFold recursive folding incurs depth and noise growth linear with each step. Ajtai commitments use Gaussian for blinding vectors in commitment and evaluation. Commitment folding implies re-randomization, increasing overhead. LatticeFold is algebraically compatible but practical suitability is questionable.

#### [HSS24](https://eprint.iacr.org/2024/306)

Hwang-Seo-Song’s PCS has $O(\sqrt{N})$ proof size and verifier time, using a Bulletproofs-style folding protocol over SIS-based commitments. Commitments use Ajtai-style matrix maps; evaluation involves one or two recursive foldings via linear coefficient combinations—similar to Breakdown’s vector splitting—avoiding deep recursion and interaction. Compared to FRI-based PCS (e.g., SLAP, Greyhound), HSS24 uses constant-round folding and amortized soundness without trapdoors.

All core operations—matrix-vector multiplication, small norm checks, and Hadamard products—are linear and generally suitable for SIMD on packed ciphertexts. Commitment is a linear map $C = A \cdot \mathbf{f}$ with known $A$, allowing homomorphic commitment generation via packed inner products. Operates over a 64-bit prime field ($q \approx 2^{64}$), matching common plaintext modulus in leveled BFV/BGV schemes. Nonlinear overhead is minimal: no trapdoors, no bit decomposition. Sum-check-style inner product checks require constant number of multiplications, but the overall circuit depth remains shallow and noise growth minimal.

Downsides: discrete Gaussian sampling; larger proofs ($\sim$MB) compared to Greyhound’s KB-scale, but this trade-off yields simpler and more FHE-friendly prover computation.

#### **Multilinear support**

Lattice-based PCS generally don’t support multilinear polynomials natively. Their algebraic structure commits to univariate or vector-structured polynomials in rings like $R_q = \mathbb{Z}_q[X]/(X^n+1)$. Encoding full multilinear structure (for Spartan-style PIOPs) requires nontrivial mapping.

Multilinear commitment is hard due to the lack of natural tensor-product encodings in $R_q$. Evaluation proofs for multilinear queries would need nested folding or interpolation, increasing depth. In HSS24, multilinear support could be added by extending commitment input to encode multilinear extensions and combining folding with batched sum-checks (Aurora style). This would preserve linearity but may raise prover overhead and proof size.

LatticeFold indirectly supports multilinear polynomials. Its folded witness representation matches the structure of multilinear R1CS. However, it uses Ajtai-based vector commitments to coefficients and then leverages the inherent connection between a vector and its multilinear extension over the hypercube to handle polynomial identity arguments. Similar trick can be considered for HSS24.

## PoD w/ proof composition

[Recall](https://hackmd.io/@timofey/r1FuxwVsJg#Public-verifiability-of-FHE-SNARK) that public verifiability in FHE-SNARK incurs performance overhead and introduces new attack vectors:

- Client overhead from generating PoDs is unavoidable but can be reduced with more efficient schemes, but for public verifier extra cost comes from verifying PoD.
- The most alarming security concern is [decryption-oracle attacks](https://hackmd.io/@timofey/ryYXSoIC1g#Decryption-oracle-attacks). According to [Checri et al.](https://eprint.iacr.org/2024/116.pdf) and [Cheon et al.](https://eprint.iacr.org/2024/127) most FHE libraries lack CPAD security. The decryption oracle, in the form of broadcasted proof decryptions, therefore creates conditions for secret key recovery.

We explore proof composition to remedy these issues.

### Full recursion

If PoD and PCS evaluation proofs are verified within the same zk-SNARK, we can keep decryptions $u, \hat{v}$ private. Besides checking batched decryption, a proof can verify the plaintext portion of the evaluation proof ([steps 3-5](#Public-verifier)). The main bottleneck would be encoding (step 3); inner products and multilinear evaluations depend on soundness parameter $\lambda$ and would likely pose a challenge. Optionally, a recursive verifier could include Merkle proofs verification. The issue is that unlike decryption, Merkle authentication is not homomorphic and cannot be amortized i.e., Merkle proofs cannot be batch-verified.

The overhead of full recursion depends on how well the outer zk-SNARK verifies the inner ones. If we extend PoD circuit to verify evaluation proof, that’s another reason to consider lattice-based PCS for FHE-SNARK, as PoD and evaluation proof would have a similar structure.

### BaseFold compression

Inspired by BrakingBase, we consider proof composition based on BaseFold to recommit to queried value decryptions. Server commits according to BrakingBase. In the testing and evaluation phase, the client, after receiving encoded linear combinations $ct[u], ct[\hat{v}]$ decrypts and commits $ct[u]$ via BaseFold PCS $(p, p^\prime), (q, q^\prime)$ and runs parallel sumchecks and batched evaluation check ([steps 6-14|BrakingBase](https://eprint.iacr.org/2024/1825.pdf#page=18)) _in plaintext_. Client can do this because after step 5 the original and encoded matrices $M, \hat{M}$, which client doesn’t know—are no longer used. Instead, client use BaseFold and Spark to prove consistency of $(p, p^\prime)$ with R1CS circuit, namely with pre-processed multilinear $\tilde{H}$.

[Step 7](https://eprint.iacr.org/2024/1825.pdf#page=18) is critical to this idea—here prover (now client) and verifier (now public verifier) run a sumcheck to check that a commitment $(p, p^\prime)$ is consistent with $\hat{v}$. In the 1st sumcheck round, they reduce the RHS (sum of composite multilinear $g$ over hypercube) to $\text{LHS} \equiv g_1(0) + g_1(1)$ check. Instead of computing $\text{LHS} = \sum_{i \in I} s_i\langle\mathbf{r}, \hat{v_i}\rangle$ on their own *in clear* (as done in BrakingBase), verifier now checks $$
\text{acc} \stackrel{?}{=} \operatorname{PoD.V}(\pi^{\mathrm{PoD}}, \mathrm{C}_{sk}, ct[\text{LHS}], g_1(0) + g_1(1))
$$ where $ct[\text{LHS}] = \sum_{i \in I} s_i\langle\mathbf{r}, ct[\hat{v_i}]\rangle$ is computed homomorphically by verifier.

The caveat is that we still indirectly reveal the decryption of $ct[\text{LHS}]$, although only one compared to before revealing everything $\{ct[u_i],u_i\}, \{ct[\hat{v_j}], \hat{v_j}\}$. Note, we don't have to verifiably decrypt $ct[u_i]$ anymore because the earlier Breakdown check is replaced with BaseFold and Spark.

Here are a few "half-baked" ideas for further addressing this:
- PoDs per inner product $\langle\mathbf{r}, ct[\hat{v_i}]\rangle$ so decryptions can be blinded by $s_i$
- Turning sumcheck into zerocheck with blinding
- If PoD is sumcheck/GKR based, step 7 can possibly be reduced to a single blinded batched sumcheck.

This construction reduces Breakdown’s quadratic proof size to quasi-logarithmic, hides most or all decryptions, and somewhat reduces PoD overhead.

## Private shared state

In our analysis document, we compared FHE-SNARK and other PPD approaches, namely [CoSNARKs & Delegated Spartan](https://hackmd.io/@timofey/r1FuxwVsJg#Appendix). One of the key factors when choosing the right approach for a given application is the private shared state requirement.

In the simplest form of PPD, there’s no shared witness—a client offloads proof generation without revealing the witness. In this model, the Delegated Spartan approach makes sense, although the exact details remain unclear. **In our future work, we intend to compare Delegated Spartan and FHE-SNARK.**

Consider the scenario where the server holds some witness required to compute a delegated SNARK, referred to as 2 party private verifiable computation (2P-PVC).

- **Verifiable private inference**: the server holds a private model or decision tree and client requests the evaluation of their private input with an integrity proof.
- **Confidential smart contract execution:** the server owns private smart contract bytecode and client requests verifiably execute a smart contract without revealing transaction details or contract logic.
- [**Delegated Private Matching for Compute (DPMC)**](https://eprint.iacr.org/2023/012.pdf)**:** the server and a client own private datasets and want to verifiably compute a function over matching identifiers without revealing non-matching data. Applications: ad conversion attribution.

Such applications can be enabled by both FHE-SNARK and CoSNARKs. Here we will focus solely on FHE-SNARK. **In the future, we plan to extend our analysis to the multiparty setting (MPVC) and compare it with CoSNARKs.**

### PCS for hybrid values

[Zhang et al.](https://eprint.iacr.org/2025/302) formalized FHE-SNARK as a form of 2P-PVC and warned about [input-dependent](https://hackmd.io/@timofey/r1FuxwVsJg#Attacks-on-FHE-SNARK) attacks when the server is allowed to have private inputs. Preventing such attacks on FHE-SNARKs requires enforcing knowledge soundness on the server’s private inputs. However, traditional _knowledge soundness_ fails because the extractor cannot decrypt messages without the FHE secret key.

A PCS for hybrid values (witnesses with both plaintext and encrypted parts) allows plaintext extraction without the FHE secret key, leveraging a _multilinear structure_ and organizing evaluations into a “cryptomix” hypercube representation, enabling efficient, structured commitments with minimal extra cost.

Where other approaches fall short:

- Commit-and-prove using hash commitments (even SNARK-friendly hashes like Poseidon) introduces significant constraint overhead, especially with many plaintext witness elements.
- Committing to the plaintext portion of the witness separately increases proof size. Multilinear PCS requires embedding both plaintext and ciphertext parts of the witness into the same hypercube dimension, necessitating padding plaintexts to match ciphertext lengths. This padding further increases both proof size and verifier work.

Constructing PCS for hybrid values requires _domain separability_ for plaintext and ciphertext values; opening a plaintext value shouldn’t involve ciphertext values. In erasure-code schemes, this rules out encoding plaintexts with ciphertexts. In Brakedown/Ligero, the committing prover represents the evaluations as a matrix and encodes its rows, so values in different rows aren’t mixed. Conversely, FRI lacks such separability because the low-degree extension encodes all values from a single vector.


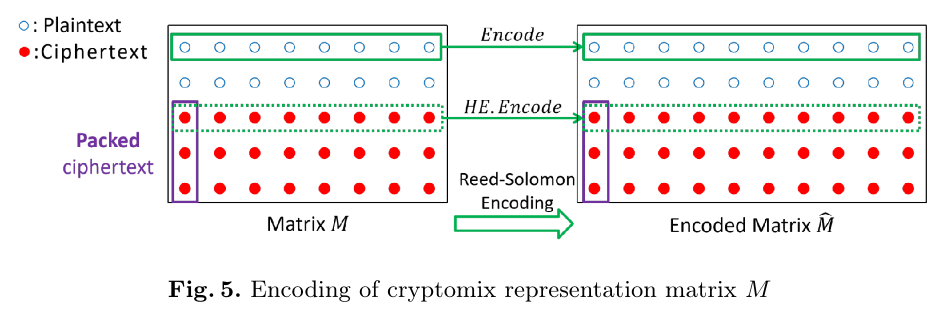
Same as [earlier](#PCS-for-encrypted-values), the prover claims knowledge of a multilinear polynomial $\tilde{f}$ such that $\tilde{f}(b) = ct[a]$. This time, $\tilde{f}$ also evaluates to a ciphertext $ct[c]$ (server's witness) at another point $d \in \{0,1\}^n$.

To prevent prover forging $ct[c]$ based on $ct[a]$, along with an earlier polynomial identity prover must additionally prove knowledge of a plaintext $c$, and what’s crucially _without revealing it_. For this, they construct a cryptomix polynomial $\tilde{f}_{\text{mix}}$ that evaluates to both encrypted witnesses $ct[a], ct[c]$ and to the plaintext $c$ at a separate point $e \in \{0,1\}^n$.

**How can the client verify that $ct[c] \equiv \operatorname{Enc}_{sk}(c)$ without learning $c$?**

The trick is in modifier encoding correctness check ([step 5](https://eprint.iacr.org/2025/302.pdf#page=42)): Let $k \in S \subseteq [2^d]$ be a subset of rows where matrix $M$ holds server's plaintext private inputs including $c$; the remaining rows $\kappa \in [2^d] \setminus S$ hold all ciphertexts including $ct[c]$. Prover sends columns $\hat{v} \in \hat{M}$ consisting encoded hybrid values including $\hat{c}, ct[\hat{c}]$; and row vector of linear combinations of *only* ciphertext rows $ct[u] = \langle r, M[\kappa,:] \rangle$. After decrypting blinded $u$ v, the modified encoding check is now $\langle r,[\hat{v}_j]_p\rangle \equiv \operatorname{Enc}(u)_j$ where $[\hat{v}_j]_p$ are $k$ first elements in $\hat{v}_j$ containing only encoded plaintexts (server's witness). Conceptually, the check goes like this: $$
\sum_{k \in S} r_k\cdot\hat{v}_{j,k} = \operatorname{Encode}\left(\sum_{\kappa \in [2^d] \setminus S} r_\kappa\cdot M[\kappa,:]\right)_j
$$This description only covers verification of the server's witness, not client’s $ct[a]$ which requires decrypting $ct[v_{j,\kappa}]$ for the client's witness. Authors also don't include PoD construction for hybrid values PCS. **In future work, we aim to formalize these missing details.**

## Conclusion

This work defines key components for building an end-to-end FHE-SNARK-based PPD system. We note R1CS-based IOPs, to be ideal for homomorphic proving due to their holographic structure. Compared to PLONK and AIR, such R1CS avoid costly non-linear constraints and allow for more flexible witness ordering, enabling SIMD-optimized ciphertext packing.

We specify a PCS for encrypted values based on Breakdown, and extend it with a PoD for public verifiability. We explore alternative PCS constructions: Among code-based schemes, _BrakingBase_ offers the good tradeoff between prover efficiency and verifier overhead. Among lattice-based approaches, _HSS24_ stands out for its simple mostly linear design that is structurally close to FHE.

To reduce PoD overhead and defend against decryption-oracle attacks, we propose strategies based on _proof composition_. One approach using client-side BaseFold wrapper offers an innovative way to hide decryptions while reducing number of verifiable decryptions and compressing final public proof.

Finally, although FHE-SNARK’s advantage in classical one-client PPD scenarios compared to competing approaches like Delegated Spartan is to be confirmed, we note it's relevance in _private shared state_ settings. We explain how PCS for hybrid values let’s server to be a second private witness source while preventing input dependent attacks. This opens up applications like verifiable inference with private models and encrypted inputs.

### Future work

1. **PPD prototype based on FHE-SNARK** with Spartan PIOP + Breakdown PCS for encrypted values; benchmarks and conclusive comparison with Delegated Spartan and CoSNARKs.
2. **FHE-SNARK with 2-party shared witness**. Specify and develop PCS for hybrid values and compatible PoD construction with the goal to demonstrate its viability in applications where server has private inputs.
3. **Testing alternative multilinear PCS** for encrypted values and **proof composition** technique based on BaseFold/WHIR.
4. **Paper** with specifications, analysis, and summary of findings and benchmarks results.

## Appendix

### PCS for packed ciphertexts

FHE efficiency relies on ciphertext packing and SIMD. This imposes certain structural considerations for the composed SNARK to leverage SIMD parallelism, particularly around PCS.

FRI encodes full-length polynomial evaluations via Reed-Solomon (RS) and FFT/NTT. Once encrypted, each packed ciphertext holds multiple evaluations, preventing SIMD amortization, because encoding must either perform costly slot permutations (for butterfly algorithm) within packed ciphertexts; or be applied separately for each ciphertext. Either way, overhead cost scales linearly in the number of ciphertexts making FRI not ideal for packed HE computation.

Breakdown/Ligero represents values as a matrix $M$, encoding each row using Reed-Solomon codes (interleaving). Ciphertexts pack values column-wise i.e., the same slot index across polynomials. Since RS encoding is identical across rows, the same linear transformation (NTT) can be homomorphically applied to each packed column via a single HE.Encode call, encoding all rows in parallel.

For example, if ciphertext values are arranged as $P$ rows and values at point $x_i$ in column $i$, then each packed ciphertext $ct_i$ holds all $M[j][i]$ (all rows at that evaluation point). Since each row is encoded identically, a single homomorphic linear transformation (HE.Encode) applied to $ct_i$ can apply NTT to all SIMD-packed values in parallel.

Although Ligero uses RS codes like FRI needing NTT, it suffices to apply a constant-layer NTT—a precompiled, fixed-depth linear circuit of scalar multiplies—across packed columns. This avoids FRI’s logarithmic depth and input-size-dependent FFTs, enabling fast SIMD-parallel encoding with low multiplicative depth, tailored to leveled FHE constraints.

#### Zero-knowledge & Succinctness

To preserve zero-knowledge and succinctness when opening ciphertext commitment and proving its decryption, it’s crucial to only reveal queried values and not the entire SIMD batch.

- **SIMD masking** could be used to selectively zero out the unwanted slot values before decryption, isolating the desired subset for verification.
- **Ring Switching:** If the subset of slots needed for verification is smaller than the total number of slots in the original ciphertext, it might be possible to switch to a smaller ring dimension that accommodates only the required number of slots, potentially simplifying the PoD process.

### Batching query PoDs

Instead of proving decryption for each opening query ciphertext individually, we can leverage FHE’s linear homomorphism to prove the correct decryption of a _random linear combination_ of ciphertexts as suggested by [Gama et al.](https://eprint.iacr.org/2024/1684.pdf#page=40) This significantly reduces client proving and public verifier’s work and proof size.

Batching involves computing a random linear combination of the claimed value ciphertexts $c\tilde{t} = \sum_{i \in [r]} \operatorname{ptMult}(ct{[q_i]}, \alpha_i)$ and a linear combination of the corresponding plaintexts $\tilde{q} = \sum_{i \in [r]} \alpha_i \cdot q_i$. Prover can then generate a single PoD ($\pi_{PoD}$) to prove that the aggregated ciphertext $c\tilde{t}$ decrypts to the aggregated plaintext $\tilde{m}$ under the committed secret key $C_{sk}$.

Note, that for soundness of a delegated SNARK and accompanied PoD, it's sufficient to only verifiably decrypt claimed values; the plaintext authentication paths (Merkle proofs in FRI queries) are directly included in the publicly verifiable proof. The public verifier then checks that authentication paths $\text{ap}_i$ that correctly connect the now-verified claimed value plaintexts $q_i$ to the corresponding Merkle roots $C_i$.