## Advanced Data Structures and Algorithms Course <!-- Put the link to this slide here so people can follow --> Thuc Nguyen @ 2023 gthuc.nguyen@gmail.com --- ## Introduction - About me - About the course - Syllabus --- ### About the course - Comprehensive - Practical - Competitive Programming - Intuitive - Python-based Lecture decks: https://hackmd.io/@thucnc/adsa-lec## --- ### Syllabus - Problem Solving Paradigms: Complete Search, Divide and Conquer, Greedy, DP - Data Structures: array, list, stack, queue, deque, heap, set, dict, tree, trie - Algorithms: Algorithm Complexity, Sorting, Searching, Text Processing - Graph theory: Graph Traversal, Paths & Cycles, Shortest Paths, Spanning Tree, Network Flow, Maximum Matching, Topological Ordering - Midcourse & End-of-course Contest and Review --- ### References * Introduction to Algorithms * Competitive Programmer’s Handbook * Competitive Programming 3 * Guide to Competitive Programming * Competitive Programming in Python * Data Structures and Algorithms in Python * Python Data Structures and Algorithms * DSAP Lê Minh Hoàng * Tài liệu giáo khoa chuyên tin (03 tập) * Intuitive demonstrations: Google, Youtube * Problem sets: ucode.vn --- ## Lecture 01. Problem Solving Paradigms - Part 1 1. Complete Search 2. Divide and Conquer --- ### 1. Complete Search - Interactive: - Loops - Generation - Recursive: - Backtracking - Backtracking with Pruning --- #### 1.1. Complete Search: Interactive - Loops - Ex1. Given three integers A, B, and C ($1 ≤ A, B, C ≤ 10000$), find three other distinct integers x, y, and z such that $x + y + z = A$, $x × y × z = B$, and $x^2 + y^2 + z^2 = C$. - Ex2. Find and display all pairs of 5-digit numbers that collectively use the digits 0 through 9 once each, such that the first number is divisible by the second. --- #### 1.1. Complete Search: Interactive - Generation: **Lexicographic** (or Dictionary) order Examples: - Ex1. Generating all **subsets** of a set of n elements. - Ex2. Generating all **permutations** of a set of n elements. --- #### 1.2. 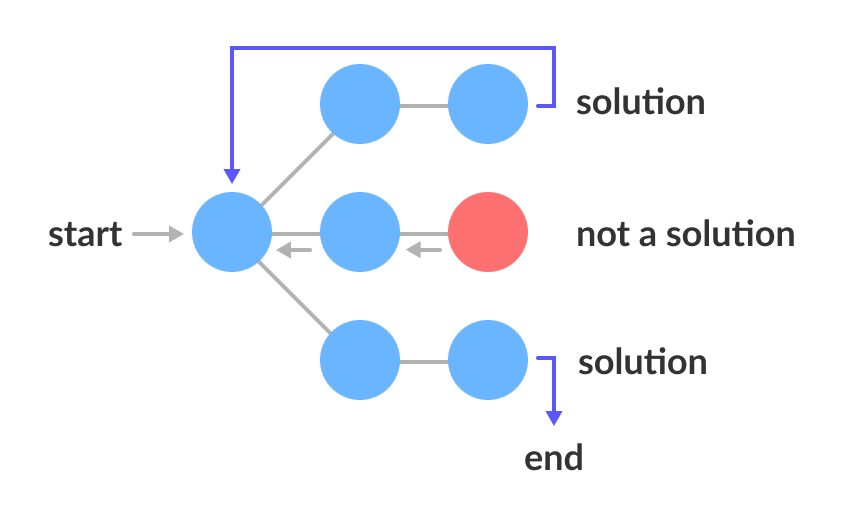Complete Search: Backtracking  --- #### 1.2. Complete Search: Backtracking ```python= def attempt(i): for v in {available values}: a[i] = v if i==n: # check result else: attempt(i+1) attempt(1) ``` --- #### 1.2. 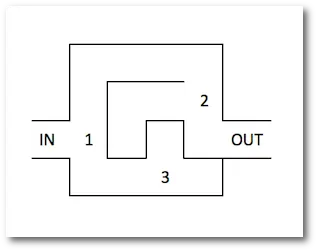Complete Search: Backtracking Find path in maze  --- #### 1.2. 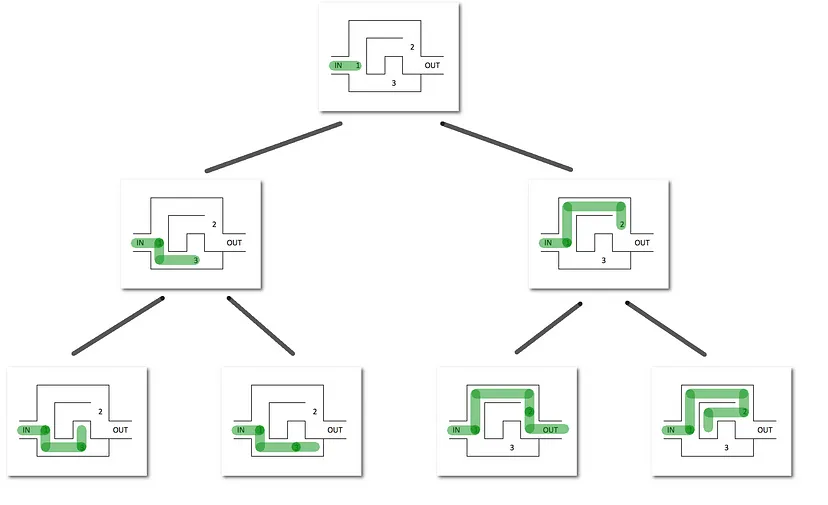Complete Search: Backtracking Find path in maze  --- #### 1.2. Complete Search: Backtracking Queens on chess board <img src="https://cdn.ucode.vn/uploads/1/upload/XmiPmPuR.png" height="70%" width="70%"/> --- #### 1.2. Complete Search: Backtracking with pruning <img src="https://cdn.ucode.vn/uploads/1/upload/RVbeivkh.png" height="70%" width="70%"/> --- #### 1.2. Complete Search: Backtracking with pruning Calculating the number of paths in an n×n grid. For n = 7, basic backtracking: **76B** recursive calls.  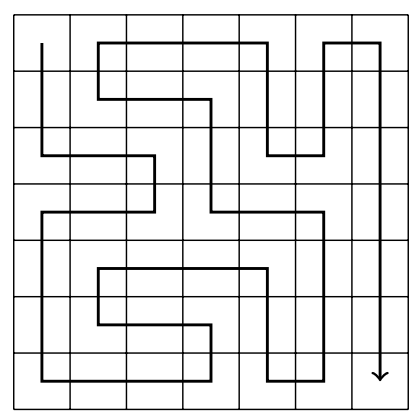--- #### 1.2. 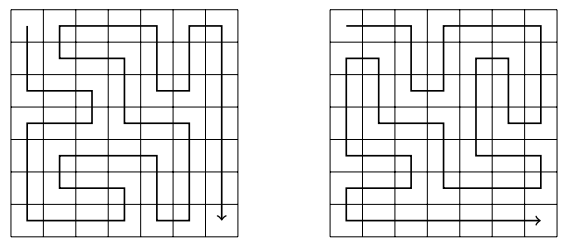Complete Search: Backtracking with pruning - Basic backtracking: **76B** recursive calls - Optimization 1: Fix first move (down or right), then multiply the result by 2 → **38B** recursive calls.  --- #### 1.2. 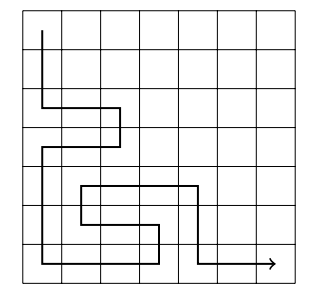Complete Search: Backtracking with pruning - Optimization 2: Stop when the path reaches the lower-right square too early → **20B** recursive calls.  --- #### 1.2. 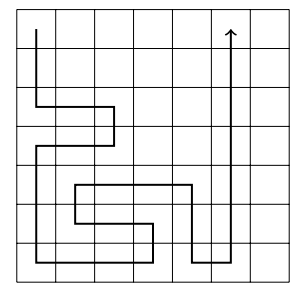Complete Search: Backtracking with pruning - Optimization 3: Stop when the path touches a wall and can turn **either left or right** → **221M** recursive calls.  --- #### 1.2. 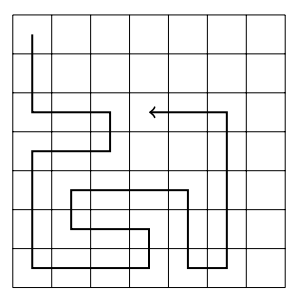Complete Search: Backtracking with pruning - Optimization 4: Stop when the path cannot continue forward and can turn **either left or right** → **69M** recursive calls.  --- ### 2. Divide and Conquer 1. **Divide** the problem into smaller instances 2. **Conquer** each of these sub-problems 3. **Combine** the sub-solutions to get the result <img src="https://mobisoftinfotech.com/resources/wp-content/uploads/2016/10/Divide-and-Conquer-Approach-to-Quality-Assurance-banner-1.png" height="70%" width="70%"/> Note: 1. of the same problem usually by half or nearly half, 2. Find sub-solutions for, (usually recursively) —which are now easier 3. (if needed) --- #### 2. Divide and Conquer: Binary search <img src="https://www.topcoder.com/wp-content/uploads/2017/07/binary-search.png" height="70%" width="70%"/> --- #### 2. Divide and Conquer: Merge Sort <img src="https://www.programiz.com/sites/tutorial2program/files/merge-sort-example_0.png" height="55%" width="55%"/> --- #### 2. Divide and Conquer: Hanoi Tower <img src="https://javainterviewpoint.com//wp-content/uploads/2016/08/Towers-Of-Hanoi.png" height="70%" width="70%"/> Note: Recursive are usually used Hard to write non recursive solution --- #### 2. Divide and Conquer: Fibonacci sequence (Bad example!)  Note: Sub problems are overlapped --- #### 2. Divide and Conquer: Meet in the middle Problem: Given a list of *n* numbers and a number *x*, is it possible to choose some numbers from the list so that their sum is *x*? For example: given the list [2, 4, 5, 9] and x = 15 → YES, x = 10 → NO. Note: Typically, we can turn a factor of 2^n into a factor of 2^(n/2) using the meet in the middle technique The idea is to divide the list into two lists A and B such that both lists contain about half of the numbers. The first search generates all subsets of A and stores their sums to a list SA. Correspondingly, the second search creates a list SB from B. After this, it suffices to check if it is possible to choose one element from SA and another element from SB such that their sum is x. This is possible exactly when there is a way to form the sum x using the numbers of the original list. --- ## The End