<style> h2{ color:#8B4746; } .blue{ color:#4A919E } </style> <font color="#4A919E">DSA 第九週講義</font> === >[name= 沈奕呈、陳睿倬][time=Mar 25,2022 ] ###### tags:`DSA` `Data Structure and Algorithm` `資料結構` `演算法` `Data Structure` `Algorithm` `tcirc39th` `社課` `臺中一中電研社` [TOC] --- ## <div class="blue">電研社</div> 社網:[tcirc.tw](https://tcirc.tw) online judge:[judge.tcirc.tw](https://judge.tcirc.tw) IG:[TCIRC_39th](https://www.instagram.com/tcirc_39th) 社課點名表單:[google 表單](https://docs.google.com/forms/d/e/1FAIpQLSdM79ScZSPDsRqUSyhKsycbnj7JRHfnuVYEAKwoeoaSmWKZng/viewform) --- ## 排序演算法 將一組資料排成特定順序的方法 ex.照數字大小，字典序...排序 --- ### 常見排序演算法 1. 氣泡排序法 2. 插入排序法 3. 選擇排序法 4. 合併排序法 5. 快速排序法 詳細概念會在最後面補充 ---- ### sort() 就算不會排序演算法，還是可以進行排序喔😁 因為c++的 `<algorithm>` 函式庫有內建`sort()`函式，可以將指定範圍內的資料進行排序 ---- 排序陣列內指定範圍的資料 ```cpp= #include <iostream> #include<algorithm> using namespace std; int main() { const int n=10;//n設為10 //example 1 int arr1[n]={7,1,6,8,4,2,9,3,5,0}; //將第0格~第n-1格間的資料排序(不含第n格) sort(arr1,arr1+n); //排序後的資料由小到大 for(int i=0;i<n;i+=1) cout<<arr1[i]<<' '; return 0; } ``` ---- ``` /*OUTPUT--- 0 1 2 3 4 5 6 7 8 9 ------------*/ ``` ---- 排序vector內指定範圍的資料 ```cpp= #include <iostream> #include<vector> #include<algorithm> using namespace std; int main() { vector<int> rank; int a,n; cin>>n; for(int i=0;i<n;i+=1){ cin>>a; rank.push_back(a); } //將第0格~最後一格間的資料排序( 不含.end() ) sort(rank.begin(),rank.end()); for(int i=0;i<n;i+=1){ cout<<rank[i]; } return 0; } ``` ---- sort()的進階用法就不贅述了，有興趣的可以點連結看(當然是自己寫的程式碼) 1. [以函式設定排序方式](https://ideone.com/D3z16w) 2. [struct型態資料，設定排序方式](https://ideone.com/yDY7lM) --- ### 「我全都要」函式庫😂 隨著stl的東西越學越多，你是不是常常忘記要加哪個標頭檔?? 小孩子才一個一個引入，我全都要!! ---- 只要引入 `#include<bits/stdc++.h>` 就可以引入所有的函示庫了喔  --- ## 分治法 (divide and conquer) 面對一個大問題，我們可以使用分治法，將大問題拆成小問題，再各自擊破，再把小問題的答案組合成整個問題的答案 ---- 分治法有三大重點 1. divide:將問題分割成數個子問題 2. conquer:若達到終止條件(問題夠小)則解決問題，否則用遞迴繼續切割問題 3. conbine:處理「橫跨數區子問題」的問題 ---- 分治法的特色在將資料二分處理，大大減少執行次數 假設列舉是以一元樹的方式一個一個處理資料，則該樹的深度是n，代表需要n輪操作才能解決n筆資料 那麼分治法就是以二元樹的方式將資料分割處理，雖然每輪依然要分別處理n筆資料，但該樹的深度是$logn$，代表只需要進行$logn$輪操作就能解決問題 ---- ### 合併排序 那我們可以將分治的方法套用到排序上。先想子問題是什麼，再想如何將子問題答案合併。 在這裡的問題很簡單，就是排序。但我們可以把排序範圍縮小，把陣列切一半，分別排序前、後陣列。此時，每次合併我們只要開一個迴圈逐步比較大小，時間複雜度為O(n)，總共要處裡(log n)次。所以總共需要O(nlog n)的時間。 ---- 1. divide:將將陣列分成前半和後半`(l~m)`、`(m~r)` (不含右界、左閉右開) 2. conquer:若該區陣列長度為1則停止(該區只有一個元素，當然可以視為排序好那區了)，否則用遞迴繼續切割問題 ---- 3. conbine:從分別排序好的左半區和右半區合併，並將整區重新排序 重新排序!?列舉的話每次合併都要花 $O(n^2)$來排序ㄟ 不是的，重新排序已分別排序好的兩組資料有比列舉更快的方法，two pointers !! ---- #### two pointers pointer(指標):pointer其實就是索引，宣告一個變數p當作陣列的索引，藉由加減p來將pointer前移或後移 而 two pointers 就是使用兩個pointers，一個在前一個在後，以特定規則移動的線性掃瞄法，而線性掃瞄一輪的複雜度是O(n) 雙層迴圈就是我們最常見的 two pointers ，進行n輪線性掃瞄，複雜度$O(n^2)$ ---- 回到主題，我們宣告pl、pr分別當左、右分區的pointer，並將初始位置分別設在該區的第一格l、m，並開一個臨時的陣列紀錄來記錄該區重新排好的資料 因為pl、pr皆位於該分區最小的位置，比較$a[pl]、a[pr]$，較小的即為整區最小的資料，將其放入臨時陣列的第一個位置，並將該pointer後移一格，繼續比較，直到兩個pointers皆到該分區的最後一個位置 ---- - 複雜度 每輪掃描O(n)，掃瞄$logn$輪，時間複雜度為$O(nlogn)$ 比列舉來排序的$O(n^2)$ 快多了吧 ---- {%youtube ZRPoEKHXTJg %} ---- ```cpp= #include <bits/stdc++.h> using namespace std; int arr[25]; void DAC(int l, int r){ if (l >= r)return; if (l +1 == r)return; int m = (l+r)/2; // 對兩邊陣列做排序 DAC(l, m); DAC(m, r); int len = r-l; int arr2[len]; // 建立一個陣列，防止兩邊陣列比較時更動到原陣列 int idx1 = l, idx2 = m; for (int i = 0; i<len;i++){ if (idx2 < r and arr[idx2] < arr[idx1]){ // 若右端陣列的最小值(當前)小於左邊的，且在當前要整理的範圍內 arr2[i] = arr[idx2++]; }else if (idx1 < m and arr[idx1] <= arr[idx2]){ // 若左端陣列的最小值(當前)小於右邊的，且在當前要整理的範圍內 arr2[i] = arr[idx1++]; }else if (idx2 == r){ // 右端所有元素都已排入陣列了，只要處理左端的 arr2[i] = arr[idx1]; }else{ // 反之，只要處裡右端的 arr2[i] = arr[idx2]; } } int j = 0; // 將已排完的陣列做更新 for (int i=l;i<r;i++){ arr[i] = arr2[j++]; } return; } int main(){ for (int i=0;i<25;i++){ arr[i] = rand() % 100 +1; cout << arr[i] << ' '; }cout << endl; DAC(0, 25); for (int i=0;i<25;i++){ cout << arr[i] << ' '; }cout << endl; return 0; } ``` ---- ### [d065: P-5-7. 大樓外牆廣告](https://judge.tcirc.tw/ShowProblem?problemid=d065) ---- 列舉行嗎? 有 n 種寬度，每種寬度有 1~n 種可能，時間複雜度為 $O(n^2)$ ，n>5000啦，不可能! 那試試分治法 ---- 1. divide:以中點 m 將大樓對半分成左右兩區 `(l~m-1)`、`(m+1~r)` 2. conquer:若寬度為一，則紀錄此區廣告面積為「1*樓高」，否則用遞迴繼續切割問題 ---- 3. conbine: 處理整區中橫跨左半區和右半區的廣告 (I)因為廣告橫跨左右半區，所以廣告貼的區域必定包含m，且廣告高度必<=`h[m]`，可以使用two pointers! 將`h[m]` 當最初廣告高度 ，寬度使用 pl、pr 向左向右延伸直到`h[pl]、h[pr]`比 `h[m]` 小 ---- 此時廣告左界為(pl)，右界為(pr)，因左右邊界高度皆比 `h[m]` 小，所以不含邊界，寬度為 `pr-pl-1`，紀錄此區廣告面積為「`h[m]*(pr-pl-1)`」 ---- (II)將高度下降，廣告高度調整為pl、pr中未超出整區邊界且高度較高的，再繼續延伸、紀錄廣告面積，不斷重複直到兩 pointers 均超出整區的邊界。 <font color="ff0000">每次紀錄廣告面積都要與「目前最大廣告面積」比較</font> ---- 左分區、右分區、橫跨左右分區  ---- 將高度下降再往左右延伸  ---- - 複雜度 使用 two pointers 掃描O(n)，掃瞄$logn$輪，時間複雜度為$O(nlogn)$ ---- ```cpp= #include <bits/stdc++.h> using namespace std; const int max_n=1e5; const int max_v=1e8; int n; long long h[max_n],max_area;//面積可能>1e9 void dac(int l,int r){ if(l>r)return; if(l==r){//conquer max_area=max(max_area,h[l]); return; } //divide int m=(l+r)/2; dac(l,m-1); dac(m+1,r); //conbine long long now_h=h[m]; int dl=m,dr=m; while(dl>=l || dr<=r){//兩邊都超過邊界才停止 while(dl>=l && h[dl]>=now_h) dl--;//注意邊界 while(dr<=r && h[dr]>=now_h) dr++;//注意邊界 max_area=max(max_area,now_h*(dr-dl-1) );//兩邊不含 //不能將高度更新為超過邊界的那邊 if(dl<l && dr>r)continue; if(dl<l)now_h=h[dr]; if(dr>r)now_h=h[dl]; if(dl<l || dr>r)continue; now_h=max(h[dl],h[dr]);//更新高度為較高一側 } } int main() { cin>>n; for(int i=0;i<n;i+=1) cin>>h[i]; max_area=0; dac(0,n-1); cout<<max_area<<'\n'; return 0; } ``` --- ## 二分搜尋法(binary search) 簡單來說，二分搜就是每次找陣列中間的元素，若元素大於尋找目標，則往陣列元素遞減處尋找。反之，往遞增處找。因此，要使用二分搜函數時，陣列必須經過排序。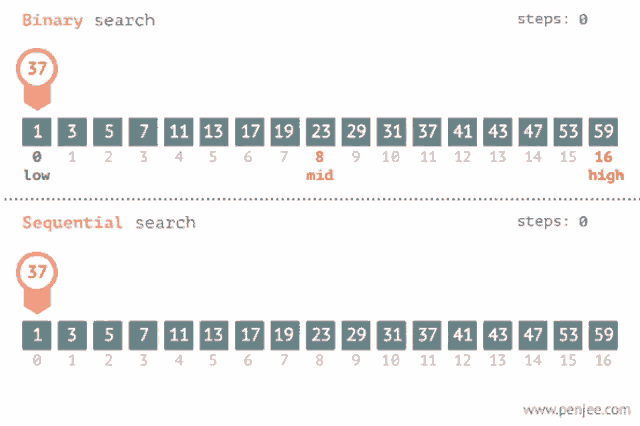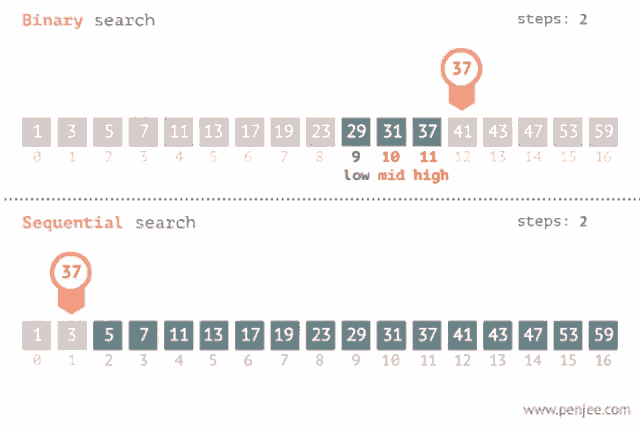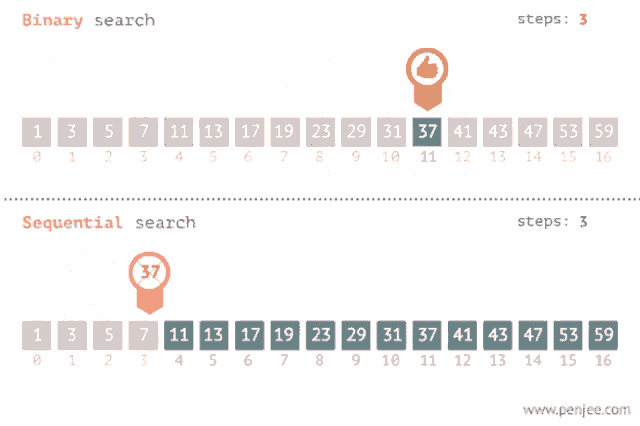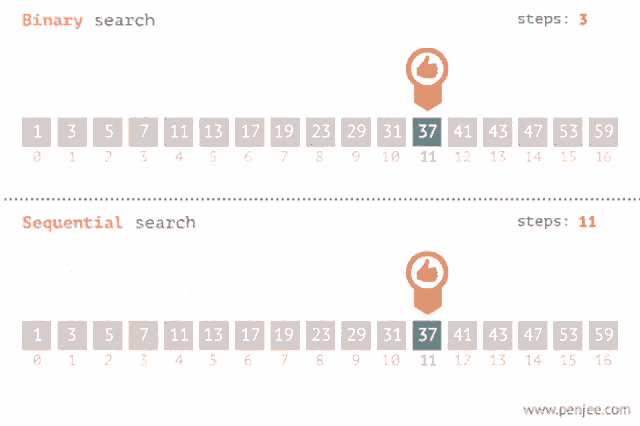 ----  [圖源](https://tenor.com/view/binary-search-sequence-search-gif-20595028) ---- ```cpp= #include <bits/stdc++.h> using namespace std; int arr[10] = {}; int binary_search(int tar, int l, int r){ if (l >= r)return -1; // 若左端idx大於右端idx --> 範圍不存在 結束 int mid = (l+r)/2; // 取中間的序號 if (arr[mid] == tar)return mid; // 若範圍中間是所求，直接回傳 else if (arr[mid] > tar){ // 範圍中間大於目標，往左端搜尋 return binary_search(tar, l, mid); }else{ // 反之，往右端搜尋 return binary_search(tar, mid+1, r); } return 0; } int main() { for (int i=0;i<10;i++){ arr[i]= rand() % 100 + 1; cout << arr[i] << ' '; }cout << endl; sort(arr, arr+10); cout << " after sort ===========\n"; for (int i=0;i<10;i++){ cout << arr[i] << ' '; }cout << endl; int idx = binary_search(arr[4], 0, 10); cout << arr[4] << endl; if (idx>0){ cout << idx << endl; }else{ cout << "not found\n"; } cout << "====================== \n"; int tmp = rand()%100+1; idx = binary_search(tmp , 0, 10); cout << tmp << endl; if (idx>0){ cout << idx << endl; }else{ cout << "not found\n"; } return 0; } ``` ---- 不過，STL裡已經幫你寫好二分搜了，分別是lower_bound和upper_bound。 兩者寫法一樣，但他們差別是，前者會回傳 x 大於等於尋找目標的iterator，而後者回傳大於目標的iterator。 **注意，lower_bound和upper_bound都是回傳iterator** ```c++= // idx = lower_bound(起始位置, 結束位置, 目標) // idx = upper_bound(起始位置, 結束位置, 目標) ``` ---- 範例: ```cpp= #include <bits/stdc++.h> using namespace std; int main() { int arr[10] = {13, 34, 25, 67, 23, 87, 56, 37, 94, 10}; sort(arr, arr+10); for (int i=0;i<10;i++){ cout << arr[i] << ' '; }cout << endl; int idx1 = lower_bound(arr, arr+10, 23) - arr; int idx2 = upper_bound(arr, arr+10, 23) - arr; // lower_bound if not found the element, return idx --> arr[idx] >= 24 int idx3 = lower_bound(arr, arr+10, 24) - arr; cout << idx1 <<' '<< arr[idx1] << endl; cout << idx2 <<' '<< arr[idx2] << endl; cout << idx3 <<' '<< arr[idx3] << endl; // if not found idx1 = lower_bound(arr, arr+10, 95) - arr; cout << idx1 << endl; // return last element's idx+1 return 0; } ``` ---- ### [範例題目: 棒棒糖比身高](https://zerojudge.tw/ShowProblem?problemid=a450) 根據題目，我們要找有多少個數字介於兩個數字之間 最笨的方法，就是先把資料排序，接著for loop迴圈掃過整個陣列，並當讀到兩個數字之間時，進行統計。 時間複雜度 --> O(nlogn) ---- 雖然這樣很快了，但是，快還要更快!!! 且資料量很大時，就要跑很久。 可以想一下哪些步驟是不需要的。 ---- 仔細想一下你會發現，我們可以不用讀取那些不在範圍內的資料。 同時，在統計個數的方法，可以改成最大值的序號減掉最小值的序號，如此一來就省去許多時間了。 時間複雜度: O(log n)*2 --> O(2log n) ---- ```cpp= #include <bits/stdc++.h> using namespace std; typedef long long ll; const int MaxS = 1e6; int main(){ // 加速讀取 ios::sync_with_stdio(0); cin.tie(0); int N, Q; ll nums[MaxS]; cin >> N >> Q; for (int i=0; i<N; i++){ cin >> nums[i]; } sort(nums, nums+N); // 資料排序 ll a, b; for (int i=0;i<Q;i++){ cin >> a >> b; // a: 最小值, b: 最大值 int idx1 = lower_bound(nums, nums+N, a) - nums; int idx2 = upper_bound(nums, nums+N, b) - nums; // ex: 2~6 數列: 0 2 3 7 9 // idx1:1 idx2:3 --> 3-1 = 2(個) // 0 2 3 7 9 if ((idx2-idx1) < 1){ cout << "The candies are too short" << endl; }else{ cout << idx2-idx1 <<endl; } } } ``` --- ## 補充 各種排序方法 [以下圖片皆取至維基百科](https://commons.wikimedia.org/wiki/Main_Page) --- ### 氣泡排序法 O(n^2) 由前向後掃描比較連續兩個位置的資料，若大小順序不合要求，則交換兩數位置，若符合則維持兩數位置，經過i輪後前i個資料即在正確位置  ---- ### 插入排序法 O(n^2) 將未排序的資料一個一個由後向前，找尋適當的位置插入新序列  ---- ### 選擇排序法 O(n^2) 選擇未排序的資料中最小的數字，與序列未排序的第零格交換位置  ---- ### 合併排序法 O(n*logn) 使用分治法，先divide再比大小合併 前面說過了，不再贅述  ---- ### 快速排序法 O(n*logn) 一樣使用分治法，但是divide的方式是選擇該區的第一個資料，分成比他小和比他大的兩區，分到所有區域剩一筆資料後停止 與合併排序不同，是先比小再divide，不須combine