<style> h2{ color:#8B4746; } .blue{ color:#4A919E } </style> <font color="#4A919E">DSA 第十一週講義</font> === >[name= 沈奕呈、陳睿倬][time=Apr 15,2022 ] ###### tags:`DSA` `Data Structure and Algorithm` `資料結構` `演算法` `Data Structure` `Algorithm` `tcirc39th` `社課` `臺中一中電研社` [TOC] --- ## <div class="blue">電研社</div> 社網:[tcirc.tw](https://tcirc.tw) online judge:[judge.tcirc.tw](https://judge.tcirc.tw) IG:[TCIRC_39th](https://www.instagram.com/tcirc_39th) 社課點名表單:[google 表單]( https://reurl.cc/02VY7K) --- ## 圖論(graph) --- ### 介紹 圖(graph)，是一種用來表示關聯、關係的概念，由數個點(vertex)與數個邊(edge)組成，邊可以用來連接任兩點，表示兩點之間有關係 ---- #### 點 個別的資料點，若沒有邊，每個點都是獨立的(與其他點沒有關係) ex.車站、人 ---- #### 邊 用來連通兩個點，表示點與點的關係，分成有向邊和無向邊 - 有向邊:代表兩個點之間具有單向關係，只有一個方向有通(可以從A點走到B點，但不能從B點走到A點) - 無向邊:代表兩個點之間具有雙向關係，雙向互通 ex.鐵路、朋友關係 --- #### 權重 有些情況下，點與點的關係與數值有關，這時可以幫邊加上權重 --- ### 圖的儲存 沒有學會如何儲存圖，就沒辦法做圖的題目，所以先來看看圖的儲存方式吧 圖的實用儲存方式有以下2種 - Adjacency matrix - Adjacency list ---- #### Adjacency matrix 中文叫「相鄰矩陣」，當點的數量為N，用一個N*N的二維陣列儲存，適合用於邊比點多很多的情況 ---- <!--https://judge.tcirc.tw/ShowProblem?problemid=d090--> ``` cpp= #include <bits/stdc++.h> using namespace std; const int max_n=1e2; const int max_m=3e4; int n,m,s; int graph[max_n][max_n];//紀錄n個點的圖 int main() { cin>>n>>m>>s; for(int i=0;i<m;i+=1){//注意是要輸入m條邊，所以放m int a,b;//起點、終點 cin>>a>>b; graph[a][b]+=1;//無向圖時須寫下一行 //graph[b][a]+=1; } for(int i=0; i<n;i+=1){ for(int j=0;j<n;j+=1) cout<<graph[i][j]<<' '; cout<<'\n'; } return 0; } ``` ---- ``` /*INTPUT--- 7 6 1 5 1 1 3 1 4 2 3 4 6 6 0 ------------*/ ``` ---- 可以看到，當點多而邊少(相對)，Adjacency matrix浪費了不少空間 但是當邊的數量接近或超過N*N，或是重複的邊常常出現的話，Adjacency matrix可以將重復的那一格加1，就能節省不少空間 ``` /*OUTPUT--- 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 ------------*/ ``` ---- #### Adjacency list 中文叫「相鄰列表」，當點的數量為N，儲存方式為，宣告一個長度為N的一維陣列，陣列資料型態使用vector或list ，適合用於點多，而邊不多的情況 ```cpp= #include <bits/stdc++.h> using namespace std; const int max_n=1e2; const int max_m=3e4; int n,m,s; vector<int> graph[max_n]; int main() { ios::sync_with_stdio(0); cin.tie(0); cin>>n>>m>>s; for(int i=0;i<m;i+=1){//注意是要輸入m條邊，所以放m int a,b;//起點、終點 cin>>a>>b; graph[a].push_back(b);//無向圖時須寫下一行 //graph[b].push_back(a); } for(int i=0; i<n;i+=1){ cout<<i<<':'; for(int j=0;j<graph[i].size();j+=1) cout<<graph[i][j]<<' '; cout<<'\n'; } return 0; } ``` ---- ``` /*INTPUT--- 7 6 1 5 1 1 3 1 4 2 3 4 6 6 0 ---------*/ ``` ---- 可以看到，當點多而邊少(相對)，Adjacency list節省了不少空間 但是當邊的數量接近或超過N*N，或是重複的邊常常出現的話，Adjacency list就會浪費不少空間 ``` /*OUTPUT--- 0: 1:3 4 2:3 3: 4:6 5:1 6:0 ------------*/ ``` ---- ### 樹 vs 圖 樹的定義較為嚴格，樹的每個點須與其他點連通，且不能形成環，圖則無此規定 --- ### 最小生成樹 全名為最小權重生成樹，也就是把一個無向圖中取出一顆樹，且樹包含所有點。 下面將簡單介紹如何求出最小生成樹。 ---- #### Kruskal_Algorithm 將每個點視作獨立的樹。接著，將權重由小到大，將兩個不同的樹連在一起。若選到的邊會讓樹形成一個環，就跳過不執行合併。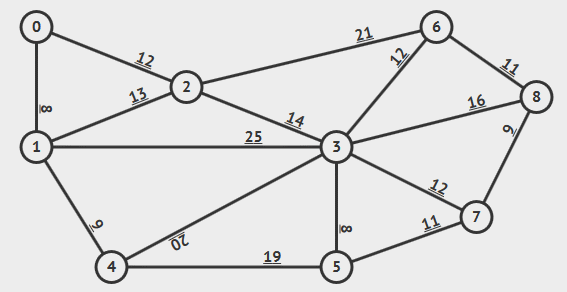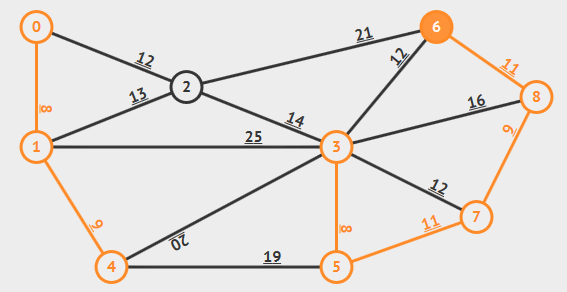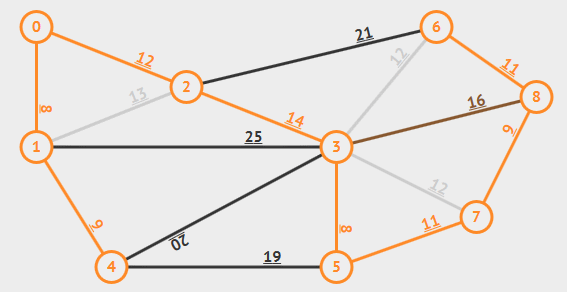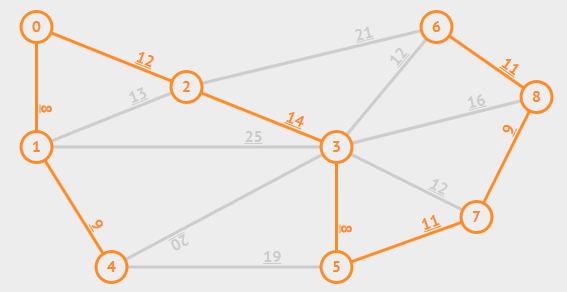  [來源](https://www.google.com/url?sa=i&url=https%3A%2F%2Fredspider110.github.io%2F2018%2F08%2F30%2F0097-algorithms-mst-kruskal%2F&psig=AOvVaw1vdtJdYReLdfaGdPfN_vC6&ust=1649854050066000&source=images&cd=vfe&ved=0CAoQjRxqFwoTCKjPvrjHjvcCFQAAAAAdAAAAABBF) ---- 這裡有個新的概念，叫DSU演算法，又稱併查集。可用於分類的問題。由兩個功能組成，查詢和合併。 套用到圖論，我們可以將起始的每個節點視為獨立的樹，而我們的目標就是將這些樹結合為最小生成樹。 在DSU裡，我們會開一個陣列root紀錄每個節點屬於哪顆樹，若兩個節點在同個樹裡，則它們的根節點相同，所以會有同一個root。 查詢的部分，就是查詢每個節點的root。 至於將兩棵樹合併成同一棵樹時，只需要將兩棵樹的root變成同一個就好。但是要先檢查它們的root是否不同，否則最後會求出一個環。 ---- ```cpp= #include <bits/stdc++.h> using namespace std; int N, S; int root[100]; struct side{ int a = a, b = b; int s = s; }; side Side[100]; bool cmp(side a, side b){ return a.s < b.s; } int FindRoot(int x){ // 查詢樹的root if (root[x] == x)return x; else return root[x] = FindRoot(root[x]); } int DSA(int a, int b){ int ra = FindRoot(a); int rb = FindRoot(b); if (ra == rb)return false; root[rb] = ra; // 兩棵不同的樹合併 return true; } int main() { cin >> N >> S; for(int i=0;i<N;i++) root[i] = i; for (int i = 0;i<S;i++){ cin >> Side[i].a >> Side[i].b >> Side[i].s; } sort(Side, Side+S, cmp); // 先將邊由小到大排好 for (int i=0;i<S;i++){ // cout << Side[i].s << ' '; int a = Side[i].a, b = Side[i].b; cout << a << ' ' << b << ' ' << Side[i].s << endl; if (DSA(a, b)){ cout << "combine successfully\n"; }else{ cout << "combine fail\n"; } } return 0; } ``` ---- https://ideone.com/LBgxEo 輸出太長，這裡就先不放 ---- #### Prim_Algorithm 選擇任一樹根作為樹根(起點)。接著，尋找尚未加入樹的點中，離樹根最近的點加入樹。重複此步驟直到所有點加進樹裡。  [來源](https://www.google.com/url?sa=i&url=https%3A%2F%2Fithelp.ithome.com.tw%2Farticles%2F10248017%3Fsc%3Dhot&psig=AOvVaw2MRAkwKrJnsN7IIlEVL1xl&ust=1650028635737000&source=images&cd=vfe&ved=0CAwQjRxqFwoTCKDf6vHRk_cCFQAAAAAdAAAAABAD) ---- ```cpp= #include <bits/stdc++.h> using namespace std; #define ppii pair<pair<int, int>, int> int N, S; int n[10]; int G[11][11]; struct cmp{ bool operator()(ppii a, ppii b){ return a.second > b.second; // 由於pq會將cmp 視為 !cmp, // 所以我們倒著寫 } }; int main() { char ch[10]; // 數字轉換成字母 for (int i=0;i<10;i++){ ch[i] = 'a'+i; } cin >> N >> S; memset(G, -1, sizeof(G)); for (int i=0;i<S;i++){ int a, b, s; cin >> a >> b >> s; G[a][b] = s; // a to b, w = s G[b][a] = s; // b to a, w = s } int cnt = 0; // 若所有點都加進樹 --> cnt == N int v[10] = {0};// 紀錄是否以加進樹裡 // init 先將a (0) 加入 priority_queue<ppii , vector<ppii>, cmp> pq; // 紀錄和樹連結的點 cnt+=1; v[0] = 1; for (int i=0;i<N;i++){ if (G[0][i] != -1) pq.push({{0, i}, G[0][i]}); } while (cnt < N){ // all nodes are in tree , then stop int a = pq.top().first.first; int b = pq.top().first.second; int s = pq.top().second; pq.pop(); if (v[b] == 1)continue; // already in tree, pass // else add it into the tree v[b] = 1;cnt++; //cout << a << ' ' << b << ' ' << s << endl; cout << ch[a] << ' ' << ch[b] << ' ' << s << endl; cout << "combine successfully\n"; for (int i=0;i<N;i++){ // 新增和樹連結的邊 if (G[b][i] != -1) pq.push({{b, i}, G[b][i]}); } } return 0; } ``` ---- output https://ideone.com/dQel5R --- ### 圖的遍歷 圖的便利方式有兩種 - BFS:廣度優先搜尋 - DFS:深度優先搜尋 ---- ### BFS 又稱廣度優先搜尋，是一種遍歷整個圖的演算法。一開始先選擇一個點最為起始點，並往周圍連結的點散開。持續上述步驟直到所有的點都被讀取過。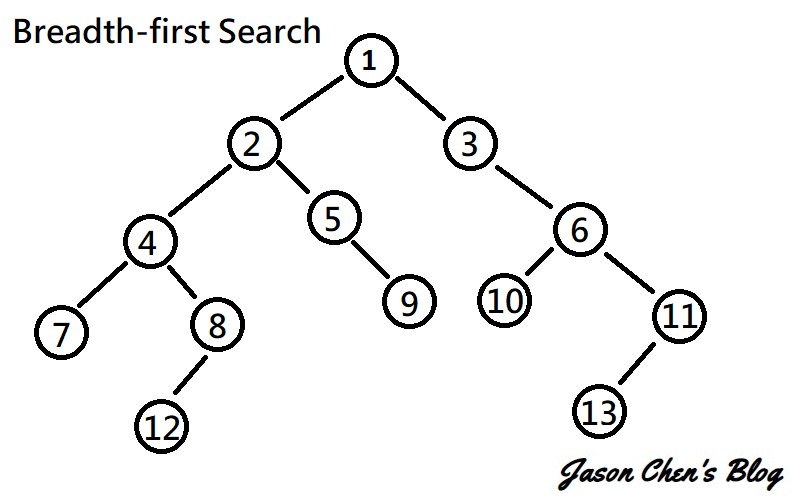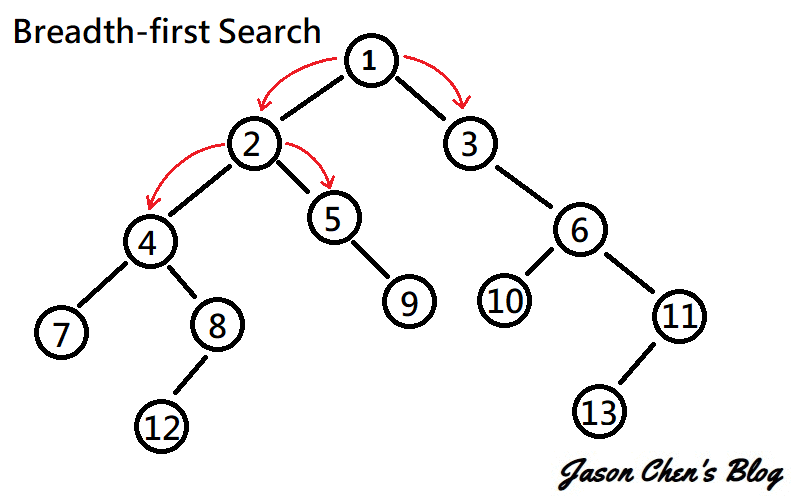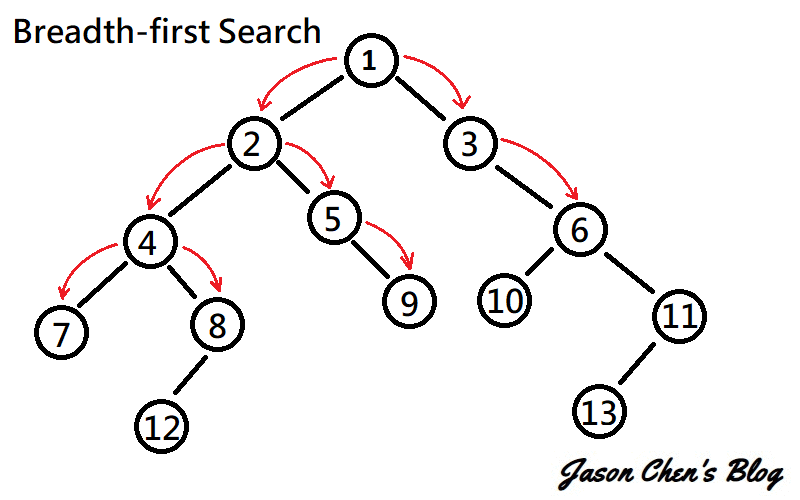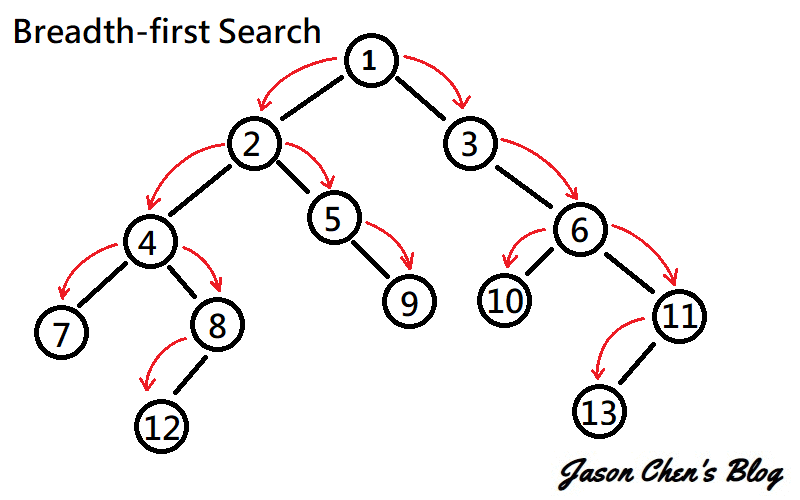  [連結](https://www.google.com/url?sa=i&url=https%3A%2F%2Fjason-chen-1992.weebly.com%2Fhome%2F-graph-searching-methods&psig=AOvVaw3Tz-mTy8ujaZLhQmiWb8Ex&ust=1650028138654000&source=images&cd=vfe&ved=0CAwQjRxqFwoTCIDs8P7Pk_cCFQAAAAAdAAAAABAD) ---- 圖論和樹的廣度優先搜尋一樣，我們可以拿queue實作。先挑選一個點，把他加進queue裡，接著讀取queue第一個元素，將和它連結的點加進queue。 所以整個流程就是: 讀取 -->pop -->加進周圍的點 -->讀取 直到沒有元素在queue裡時，我們可以停止了，因為已經拜訪過每個和出發點有連通的點了。 要注意的是，不要將已被拜訪過的元素加進queue裡，否則程式不會停止(因為會永遠讀不完)。所以可以開個陣列紀錄是否已走訪過該元素。 為了實際了解bfs的應用，我們參考下面的例題。 ---- 套用到圖論也是相同概念  [來源](https://www.google.com/url?sa=i&url=https%3A%2F%2Fvictorqi.gitbooks.io%2Fswift-algorithm%2Fcontent%2Fbreadth-first_search_bfs.html&psig=AOvVaw2peftVZi5zcdJcejsYhJMx&ust=1649855906983000&source=images&cd=vfe&ved=0CAoQjRxqFwoTCPC19K3OjvcCFQAAAAAdAAAAABAX) ---- ### 例題: [倒水時間](https://zerojudge.tw/ShowProblem?problemid=d406) 這題是非常典型的bfs應用，雖然不明顯看出他是一個圖。不過可以把每個水管看成是一個點，所以此圖變成一個有向圖(方向由上而下，往右或往左)，兩相鄰的點形成一邊。 ---- 0 0 1 0 0 0 0 1 1 0 0 1 1 1 1 1 1 0 0 0  ---- 由於題目已經指定由上面倒水，所以我們將第一排的點都設為1。接著將第一排的水管都加進queue裡。 後面就簡單了，重複執行上述我們所說的步驟。 至於往上的水管，就只是要多拜訪一個元素。 ```cpp= #include <bits/stdc++.h> using namespace std; int const MaxN = 101; int N, M; int S; int G[101][101]; int a[101][101]; bool Inrange(int r, int c){ if (r >= 0 and r < N and c >= 0 and c < M)return true; else return false; } void bfs1(){ int dc[3] = {1, -1, 0}; int dr[3] = {0,0, 1}; deque<pair<int, int>> dq; // 設定空queue for (int i=0;i<M;i++){ // 初始化第一排的水管 if (G[0][i] == 0)cout << 0 << ' '; else{ cout << 1 << ' '; a[0][i] = 1; dq.push_back({0, i}); // 將水管加進dq } }cout << endl; //cout << "=================\n"; while (dq.empty() == 0){ //cout << dq.size() << endl; int r = dq.front().first; // 讀取dq節點 int c = dq.front().second; //cout << r << ' ' << c << endl; dq.pop_front(); for (int k=0;k<3;k++){ // 拜訪周圍的點 int nxt_r = r + dr[k]; int nxt_c = c + dc[k]; if (Inrange(nxt_r, nxt_c) and G[nxt_r][nxt_c] == 1 and a[nxt_r][nxt_c] == 0){ // 若該點為水管，則時間就是上個節點+1 a[nxt_r][nxt_c] = a[r][c] + 1; dq.push_back({nxt_r, nxt_c}); // 記得加進queue }else{ continue; // 若不是水管，代表無節點，跳過 } } } for (int i=1;i<N;i++){// 輸出answer for (int j=0;j<M;j++){ if (a[i][j] == 0)cout << '0' << ' '; else cout << a[i][j] << ' '; }cout << endl; } } void bfs2(){ int dc[4] = {1, -1, 0, 0}; int dr[4] = {0, 0, -1, 1}; deque<pair<int, int>> dq; for (int i=0;i<M;i++){ if (G[0][i] == 0)cout << 0 << ' '; else{ cout << 1 << ' '; a[0][i] = 1; dq.push_back({0, i}); } }cout << endl; //cout << "=================\n"; while (dq.empty() == 0){ //cout << dq.size() << endl; int r = dq.front().first; int c = dq.front().second; //cout << r << ' ' << c << endl; dq.pop_front(); for (int k=0;k<4;k++){ int nxt_r = r + dr[k]; int nxt_c = c + dc[k]; if (Inrange(nxt_r, nxt_c) and G[nxt_r][nxt_c] == 1 and a[nxt_r][nxt_c] == 0){ a[nxt_r][nxt_c] = a[r][c] + 1; dq.push_back({nxt_r, nxt_c}); }else{ continue; } } } for (int i=1;i<N;i++){ for (int j=0;j<M;j++){ if (a[i][j] == 0)cout << '0' << ' '; else cout << a[i][j] << ' '; }cout << endl; } } int main() { ios::sync_with_stdio(0); cin.tie(0); int t = 1; while (cin >> S){ cin >> N >> M; memset(a, 0, sizeof(a)); for (int i=0;i<N;i++){ for (int j=0;j<M;j++) cin >> G[i][j]; } cout << "Case " << t++ <<":" << endl; if (S == 1) bfs2(); else bfs1(); } return 0; } ``` --- ### DFS 又稱深度優先搜尋  [圖源](https://zh.wikipedia.org/wiki/%E6%B7%B1%E5%BA%A6%E4%BC%98%E5%85%88%E6%90%9C%E7%B4%A2) ---- 造訪順序 1.由root當起點，選擇一個child拜訪，再由這個node(節點)繼續選擇一個child拜訪，不斷重複直到遇到leaf(沒有子節點) 2.從現在這一層sbiling(同層的其他節點)中選一個當起點，執行步驟1，不斷重複直到該層的sbiling都已經拜訪過 3.處理往上一層的其他sbiling，執行步驟2，不斷重複直到回到root那一層 可以發現我們在過程中都是先處理剛加入的節點，所以適合用stack--先進先出的概念來實做 ---- 作法: 1. 將起點加入stack 2. 紀錄 .top()的元素A，然後.pop() 3. 將A能連到的點全部.push()進去 4. 重複動作直到stack變成空的(代表有與起點連通的點均已拜訪過了) ---- ### 例題: [觀光景點](https://zerojudge.tw/ShowProblem?problemid=c812) 有n個點，n-1個邊，任兩點間一定會有單一路徑連通(代表這是一棵樹)，請求出與起點相關性大於等於q的景點數量(不包含起點本身) 兩景點間的相關性為沿路的邊中，權重最小的，所以如果在行經的路線中遇到權重小於題目要求的，就不用再走下去了(因為之後遇到的景點關連性都會小於q) ---- 換句話說，當邊的權重<q，那條邊就可以直接不要連了，反正通過那條路後的所有景點都不符合題目要求，<font color="#ff0000">所以我們不須額外紀錄邊的權重</font>，只需要遍歷與起點連通的所有點，並記錄這些點的數量就可以了。 <font color="#ff0000">注意!</font>:需要另外開一個一維陣列紀錄每個點有沒有被走訪過，有被走訪過的點不能再走(不然你的遍歷永遠不會結束) ---- 我們這次試試看用dfs的方式遍歷吧(要用 bfs 或是 dsu 也可以) 邊和點差不多，且不用紀錄權重，可以用adjacency list，不過點的數量不算太多，要用adjacency matrix也行 ---- ```cpp= #include <bits/stdc++.h> using namespace std; const int max_n=5e3; const int max_e=5e3-1; const int max_q=1e9; int n,v,q; vector<int> to[max_n+1];//點從1開始 vector<int> stk; bool flag[max_n+1];//紀錄點有沒有拜訪過 int main() { cin>>n>>v>>q;//點的數量,起點,相關性 n-=1;//邊的數量 while(n-->0){ int i,j,r; cin>>i>>j>>r;//兩點,權重 if(r<q) continue; to[i].push_back(j); to[j].push_back(i);//無向圖 } int ans=0; stk.push_back(v);//起點放入stack while(stk.empty()==0){//當stack不是空的 int now=stk.back(); stk.pop_back(); flag[now]=1;//紀錄已經拜訪過此點 //等同於 int nxt=to[now].begin;nxt!=to[now].end();nxt++ for(int nxt : to[now]){ if(flag[nxt]) continue;//此點已拜訪過 stk.push_back(nxt); ans+=1; } } cout<<ans<<'\n'; return 0; } ```