---
tags: 競プロ
---
# $k$-d tree のお手軽実装について

こんにちは、競技プログラミングをやっている [tatyam](https://trap.jp/author/tatyam/) と申します。私のお気に入りのデータ構造は [$k$-d tree](https://en.wikipedia.org/wiki/K-d_tree) です。

<blockquote class="twitter-tweet"><p lang="ja" dir="ltr">PAST-N : kDTree書くのたのし〜 <a href="https://t.co/s5tB9e4piP">pic.twitter.com/s5tB9e4piP</a></p>&mdash; tatyam (@tatyam_prime) <a href="https://twitter.com/tatyam_prime/status/1256869124027760640?ref_src=twsrc%5Etfw">May 3, 2020</a></blockquote> <script async src="https://platform.twitter.com/widgets.js" charset="utf-8"></script>

<blockquote class="twitter-tweet"><p lang="ja" dir="ltr">kDTree さいこー！<a href="https://t.co/diMEs3KAhM">https://t.co/diMEs3KAhM</a></p>&mdash; tatyam (@tatyam_prime) <a href="https://twitter.com/tatyam_prime/status/1376121506577588224?ref_src=twsrc%5Etfw">March 28, 2021</a></blockquote> <script async src="https://platform.twitter.com/widgets.js" charset="utf-8"></script>

<blockquote class="twitter-tweet"><p lang="ja" dir="ltr">E : kDTree ありがとう…<br>平面走査したくないので 3 次元 kDTree をする<br>O(n + m log m + k m^(2/3))<br>TLE する印象しかなかったんだけど 795 ms で通った</p>&mdash; tatyam (@tatyam_prime) <a href="https://twitter.com/tatyam_prime/status/1401903018149179398?ref_src=twsrc%5Etfw">June 7, 2021</a></blockquote> <script async src="https://platform.twitter.com/widgets.js" charset="utf-8"></script>

## できること

- [$k$-d tree](https://en.wikipedia.org/wiki/K-d_tree) は、$k$ 次元空間上の点の集合を管理することができます。ここで、$k$ は十分小さな定数 ( $2$ または $3$ くらい) です。
- 軸に並行な $k$ 次元矩形上にある点の個数を $O(k \cdot N^{1-1/k})$ で取得することができます。 ( $k = 2$ のとき $O(\sqrt N)$ )
- **入力が全てランダムであるとき**、ある点に最も近い点を $O(\log N)$ で取得することができます。
- 各点に値を載せることができ、軸に並行な $k$ 次元矩形上にある点に載っている値を可換モノイドで取得できます。(和、min / max など)
- 各点に載せた値を遅延セグメント木のように変化させることができます。(加算、代入など)
- 点の挿入・削除が $O(\log N)$ でできます。(この場合、平衡が必要になります。)

## $k$-d tree とは


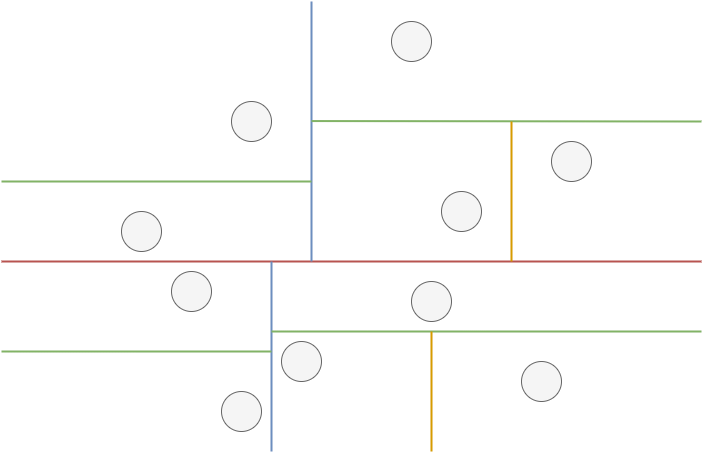
↑ $k$-d tree のイメージ図。領域を縦横交互に、点の数が半分になるように分割する。

https://www.slideshare.net/okuraofvegetable/ss-65377588
https://ja.wikipedia.org/wiki/Kd%E6%9C%A8

とか読むと良いんじゃないでしょうか

## お手軽 $k$-d tree

点の挿入・削除がなく、矩形クエリしかしないときの $k$-d tree を簡単に実装します。こういう木構造を簡単にするポイントは、葉木 (葉にしか要素を持たない木) にすることです。

void chmin(int& a, int b){ if(a > b) a = b; }
void chmax(int& a, int b){ if(a < b) a = b; }

struct kDTree{
    using T = pair<int, int>;
    using Iter = vector<T>::iterator;
    kDTree *l = nullptr, *r = nullptr;
    // 矩形クエリのために x / y 座標の最小値と最大値を持つ
    // 挿入・削除はないので、何の要素を持っているかは必要ない (要素を持っている葉と要素を持っていないそれ以外のノードを同じように扱える)
    int xmin = INT_MAX, xmax = INT_MIN, ymin = INT_MAX, ymax = INT_MIN, size = 0;
    kDTree(Iter begin, Iter end, bool divx = true){
        // vector<T> で渡してもいいですが、コピーコストがかかるので in-place に
        for(auto p = begin; p != end; p++){
            auto [x, y] = *p;
            chmin(xmin, x);
            chmax(xmax, x);
            chmin(ymin, y);
            chmax(ymax, y);
        }
        size = int(end - begin);
        if(size <= 1) return;
        // 葉木なので x / y 座標で半分に分けて再帰
        auto cen = begin + size / 2;
        // 縦横交互に分ける
        if(divx){
            nth_element(begin, cen, end, [](T a, T b){ return a.first < b.first; });
        }
        else{
            nth_element(begin, cen, end, [](T a, T b){ return a.second < b.second; });
        }
        l = new kDTree(begin, cen, !divx);
        r = new kDTree(cen, end, !divx);
    }
    // [x1, x2] * [y1, y2] にある点の個数を数える
    int count(int x1, int x2, int y1, int y2) const {
        // [xmin, xmax] * [ymin, ymax] と [x1, x2] * [y1, y2] に共通部分がない
        if(x2 < xmin || xmax < x1 || y2 < ymin || ymax < y1) return 0;
        // [xmin, xmax] * [ymin, ymax] 全体が [x1, x2] * [y1, y2] に含まれている
        if(x1 <= xmin && xmax <= x2 && y1 <= ymin && ymax <= y2) return size;
        // [xmin, xmax] * [ymin, ymax] の一部が [x1, x2] * [y1, y2] に含まれている -> 子に任せる
        return l->count(x1, x2, y1, y2) + r->count(x1, x2, y1, y2);
    }
};

### 追記

`xmax - xmin` と `ymax - ymin` のうち長い方で分けるコードを最初は書いていましたが、このコードでは、$N$ 個の点が `xmax - xmin`${}=1,$ `ymax - ymin`${}=N$ のような細長い領域にあると、取得クエリが $\Theta(N)$ かかってしまう場合があることを [@noshi91](https://trap.jp/author/noshi91/) にご指摘いただきました。
しかし、これを想定して落とすことはかなり難しいので、AC してしまうことが多いと思われます。

## 問題を解く

### [PAST2 N - ビルの建設](https://atcoder.jp/contests/past202004-open/tasks/past202004_n)

> $2$ 次元平面上に正方形の領域が $N$ 個あり、$i$ 個目の領域は $[x_i, x_i + D_i] \times [y_i, y_i + D_i]$ で、コストは $C_i$ です。
> $Q$ 個のクエリに答えてください。
> - 点 $(A, B)$ を含む全ての領域のコストの和を出力
>
> $N ≤ 5 \times 10^4,\ Q ≤ 10^5$

正方形領域に $C_i$ のコストを加算なので、imos 法を適用して累積和を取るだけにしましょう。
この後、疎な点集合の $2$ 次元累積和を取るのに、平面走査 + 座標圧縮 + BIT をしがちですが、Range Tree… は実装が大変ですし、その代わりに $k$-d tree を使ってみましょう。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
void chmin(int& a, int b){ if(a > b) a = b; }
void chmax(int& a, int b){ if(a < b) a = b; }


using T = array<int, 3>;
struct kDTree{
    using Iter = vector<T>::iterator;
    kDTree *l = nullptr, *r = nullptr;
    int xmin = INT_MAX, xmax = INT_MIN, ymin = INT_MAX, ymax = INT_MIN;
    ll sum = 0;
    kDTree(Iter begin, Iter end, bool dixx = true){
        for(auto p = begin; p != end; p++){
            auto [x, y, w] = *p;
            chmin(xmin, x);
            chmax(xmax, x);
            chmin(ymin, y);
            chmax(ymax, y);
            sum += w;
        }
        const int size = int(end - begin);
        if(size <= 1) return;
        auto cen = begin + size / 2;
        if(divx){
            nth_element(begin, cen, end, [](T& a, T& b){ return a[0] < b[0]; });
        }
        else{
            nth_element(begin, cen, end, [](T& a, T& b){ return a[1] < b[1]; });
        }
        l = new kDTree(begin, cen, !divx);
        r = new kDTree(cen, end, !divx);
    }
    // [-INF, x] * [-INF, y] にある点の重みを数える
    ll get(int x, int y) const {
        // [xmin, xmax] * [ymin, ymax] と [-INF, x] * [-INF, y] に共通部分がない
        if(x < xmin || y < ymin) return 0;
        // [xmin, xmax] * [ymin, ymax] 全体が [-INF, x] * [-INF, y] に含まれている
        if(xmax <= x && ymax <= y) return sum;
        // [xmin, xmax] * [ymin, ymax] の一部が [x1, x2] * [y1, y2] に含まれている -> 子に任せる
        return l->get(x, y) + r->get(x, y);
    }
};
int main(){
    int N, Q;
    cin >> N >> Q;
    vector<T> a;
    while(N--){
        int x, y, D, C;
        cin >> x >> y >> D >> C;
        D++;
        // imos 法
        a.push_back({x, y, C});
        a.push_back({x + D, y + D, C});
        a.push_back({x, y + D, -C});
        a.push_back({x + D, y, -C});
    }
    kDTree tree(a.begin(), a.end());
    while(Q--){
        int A, B;
        cin >> A >> B;
        cout << tree.get(A, B) << '\n';
    }
}

https://atcoder.jp/contests/past202004-open/submissions/29400829

### その 2

$k$-d tree は遅延セグ木のようなことができるということなので、矩形範囲にある点の重みを $C_i$ 加算するクエリで解いてみましょう。
加算クエリは可換なクエリなので、遅延評価部分を伝播させる必要がありません。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
void chmin(int& a, int b){ if(a > b) a = b; }
void chmax(int& a, int b){ if(a < b) a = b; }


using T = pair<int, int>;
struct kDTree{
    using Iter = vector<T>::iterator;
    kDTree *l = nullptr, *r = nullptr;
    int xmin = INT_MAX, xmax = INT_MIN, ymin = INT_MAX, ymax = INT_MIN;
    ll lazy = 0;
    kDTree(Iter begin, Iter end, bool divx = true){
        for(auto p = begin; p != end; p++){
            auto [x, y] = *p;
            chmin(xmin, x);
            chmax(xmax, x);
            chmin(ymin, y);
            chmax(ymax, y);
        }
        const int size = int(end - begin);
        if(size <= 1) return;
        auto cen = begin + size / 2;
        if(divx){
            nth_element(begin, cen, end, [](T& a, T& b){ return a.first < b.first; });
        }
        else{
            nth_element(begin, cen, end, [](T& a, T& b){ return a.second < b.second; });
        }
        l = new kDTree(begin, cen, !divx);
        r = new kDTree(cen, end, !divx);
    }
    // [x1, x2] * [y1, y2] にある点に C を加算
    void add(int x1, int x2, int y1, int y2, int C){
        // [xmin, xmax] * [ymin, ymax] と [x1, x2] * [y1, y2] に共通部分がない
        if(x2 < xmin || xmax < x1 || y2 < ymin || ymax < y1) return;
        // [xmin, xmax] * [ymin, ymax] 全体が [x1, x2] * [y1, y2] に含まれている
        if(x1 <= xmin && xmax <= x2 && y1 <= ymin && ymax <= y2){
            lazy += C;
            return;
        }
        // [xmin, xmax] * [ymin, ymax] の一部が [x1, x2] * [y1, y2] に含まれている
        l->add(x1, x2, y1, y2, C);
        r->add(x1, x2, y1, y2, C);
    }
    // [x, x] * [y, y] にある点の重みを数える
    ll get(int x, int y) const {
        // [xmin, xmax] * [ymin, ymax] と [x, x] * [y, y] に共通部分がない
        if(x < xmin || xmax < x || y < ymin || ymax < y) return 0;
        // [xmin, xmax] * [ymin, ymax] 全体が [x, x] * [y, y] に含まれている
        if(x == xmin && xmax == x && y == ymin && ymax == y) return lazy;
        // [xmin, xmax] * [ymin, ymax] が [x1, x2] * [y1, y2] を含んでいる
        return lazy + l->get(x, y) + r->get(x, y);
    }
};
int main(){
    int N, Q;
    cin >> N >> Q;
    vector<array<int, 4>> land(N);
    vector<T> query(Q);
    for(auto& [x, y, D, C] : land) cin >> x >> y >> D >> C;
    for(auto& [A, B] : query) cin >> A >> B;
    auto tree = [query]() mutable {
        return kDTree(query.begin(), query.end());
    }();
    for(auto [x, y, D, C] : land) tree.add(x, x + D, y, y + D, C);
    for(auto [A, B] : query) cout << tree.get(A, B) << '\n';
}

https://atcoder.jp/contests/past202004-open/submissions/29401260

### [ABC234 Ex - Enumerate Pairs](https://atcoder.jp/contests/abc234/tasks/abc234_h)

> $2$ 次元平面上に $N$ 個の点があります。ユークリッド距離が $K$ 以下であるような点の組を全て列挙してください。
> $N ≤ 2 \times 10^5,$ (出力する組の個数)${}≤ 4 \times 10^5$

ある点から距離 $K$ 以下の点を列挙…　これは $k$-d tree ！
本来は worst $Θ(N)$ / query ですが、(出力する組の個数)${}≤ 4 \times 10^5$ の制約のおかげで、円形クエリであってもいい感じの計算量が保証されます。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
void chmin(int& a, int b){ if(a > b) a = b; }
void chmax(int& a, int b){ if(a < b) a = b; }


using T = array<int, 3>;
struct kDTree{
    using Iter = vector<T>::iterator;
    kDTree *l = nullptr, *r = nullptr;
    // 円形クエリのために x / y 座標の最小値と最大値を持つ
    int xmin = INT_MAX, xmax = INT_MIN, ymin = INT_MAX, ymax = INT_MIN;
    // 1 要素しか持っていない時の index
    int idx = -1;
    kDTree(Iter begin, Iter end){
        for(auto p = begin; p != end; p++){
            auto [x, y, i] = *p;
            chmin(xmin, x);
            chmax(xmax, x);
            chmin(ymin, y);
            chmax(ymax, y);
        }
        const int size = int(end - begin);
        if(size == 1) idx = (*begin)[2];
        if(size <= 1) return;
        auto cen = begin + size / 2;
        if((unsigned)xmax - (unsigned)xmin > (unsigned)ymax - (unsigned)ymin){
            // 長い方で分ける (正方形に近い方が円形クエリの効率がいい)
            nth_element(begin, cen, end, [](T& a, T& b){ return a[0] < b[0]; });
        }
        else{
            nth_element(begin, cen, end, [](T& a, T& b){ return a[1] < b[1]; });
        }
        l = new kDTree(begin, cen);
        r = new kDTree(cen, end);
    }
    // sqrt(dx^2 + dy^2) ≤ K
    static bool inside(int dx, int dy, int K){
        return ll(dx) * dx + ll(dy) * dy <= ll(K) * K;
    }
    // (x, y) から距離 K 以下の点を f に報告する
    template<class F> void get(int x, int y, int K, F f) const {
        // [xmin, xmax] * [ymin, ymax] と ((x, y) から半径 K 以内) に共通部分がない
        if(!inside(clamp(x, xmin, xmax) - x, clamp(y, ymin, ymax) - y, K)) return;
        // 葉なら idx を報告
        if(idx != -1){
            f(idx);
            return;
        }
        l->get(x, y, K, f);
        r->get(x, y, K, f);
    }
};
int main(){
    int N, K;
    cin >> N >> K;
    vector<T> A(N);
    for(auto& [x, y, i] : A) cin >> x >> y;
    for(int i = 0; i < N; i++) A[i][2] = i;
    vector<pair<int, int>> ans;
    kDTree tree(A.begin(), A.end());
    for(auto [x, y, i] : A) tree.get(x, y, K, [&, i = i](int j){ if(i < j) ans.emplace_back(i + 1, j + 1); });
    sort(ans.begin(), ans.end());
    cout << ans.size() << '\n';
    for(auto [x, y] : ans) cout << x << ' ' << y << '\n';
}

https://atcoder.jp/contests/abc234/submissions/29417326