# Projeto de fonte de corrente cascode com rede de polarização CMOS

**Aluno:** Maurício Taffarel
**Número:** 24

## Objetivos do projeto

Os objetivos deste trabalho são:
- (i) o dimensionamento dos transistores de uma fonte cascode $M_1$ e $M_2$, ilustrados na Fig. 1, bem como dos transistores dos divisores de tensão a carga ativa CMOS, $M_3$, $M_4$, $M_5$ e $M_6$, que devem prover os potenciais a serem aplicados aos terminais de porta dos primeiros;
- (ii) a simulação dos circuitos para aferição do desempenho.

<center>


###### Figura 1 - Topologia do circuito
</center>

As especificações do projeto são:

- $I_{OUT} = 240\mu A$
- $V_{OUTmáx} = 0.1V$

Os dados do projeto:

- $V_{DD} = 0.6V$
- $V_{SS} = -0.6V$
- $W_{min} = L_{min} = 0.12\mu m$

Parâmetros tecnológicos:

<center>

| $V_{T0n}$ (V) | $V_{T0p}$ (V) | $n_n$ | $n_p$ | $I_{Ssqn}$ (nA) | $I_{Ssqp}$ (nA) |
|:-------------:|:-------------:|:------:|:------:|:---------------:|:---------------:|
| 0.3618 | -0.3554 | 1.3790 | 1.2952 | 353.38 | 49.514 |

</center>

## 1. Projeto da fonte cascode

A topologia da fonte cascode está representado a seguir:

<center>


###### Figura 2 - Topologia fonte cascode
</center>

De acordo com a figura $(2)$, para garantir a região de saturação para os transistores $M_1$ e $M_2$, :

$$
V_{DD}-v_{OUT}>v_{SDmax1}+v_{SDmax2}
\tag{1}
$$

No modelo **ACM**, a tensão de limiar de saturação $v_{SDmáx}$ pode ser determinado por:

$$
v_{SDmax} = \phi_{t}\left(\sqrt{i_{f}+1}+3\right)
\tag{2}
$$

Substituindo $(2)$ em $(1)$ para cada transistor canal P:

$$
v_{OUTmáx}=V_{DD}-\phi_{t}\left(\sqrt{i_{f1}+1}+\sqrt{i_{f2}+1}+6\right)
\tag{3}
$$

Através da equação $(3)$ pode-se determinar a excursão. Analogamente, para $M_2$ permanecer em saturação:

$$
v_{S2}-v_{OUT}=v_{SD2}>\phi_{t}\left(\sqrt{i_{f2}+1}+3\right)\\
v_{S2}>\phi_{t}\left(\sqrt{i_{f2}+1}+3\right)+v_{OUT}
\tag{4}
$$

A tensão $v_{S2}$ pode ser determinada também através do terminal de substrato:
$$
v_{SB2}=v_{S2}-V_{DD}=V_{P2}+\phi_{t}\cdot f\left(i_{f2}\right)\\
v_{S2}=V_{P2}+\phi_{t}\cdot f\left(i_{f2}\right)+V_{DD}
\tag{5}
$$

Comparando as equações $(4)$, $(5)$ e utilizando a apróximação para tensão de pinchoff $V_p\cong \frac{V_{GB}-V_{T0}}{n}$ é possível determinar o valor mínimo para a tensão de porta $V_{GG}$ em $M_2$:

$$
V_{GG2}\gt n_{p}\left(v_{OUTmáx}+5\phi_{t}-\phi_{t}\ln\left(\sqrt{i_{f2}+1}-1\right)\right)-\left(n_{p}-1\right)V_{DD}+V_{T0p}
\tag{6}
$$

> O valor de tensão máximo pode ser determinado através da equação $(3)$

Do mesmo modo, para garantir $M_1$ em saturação:
$$
V_{DD}-v_{S2}=-v_{DB}=-\left(V_{P2}+\phi_{t}\cdot f\left(i_{f2}\right)\right)>\phi_{t}\left(\sqrt{i_{f1}+1}+3\right)=V_{DSsat1}\\
i_{f1}<\left(-f\left(i_{f2}\right)-\frac{V_{GG2}-V_{DD}-V_{T0p}}{\phi_{t}n_{p}}-3\right)^{2}-1
\tag{7}
$$

Com o uso da equação anterior $(7$), tomando um valor mínimo como $i_{f1}=0$, obtemos o valor de $V_{GG2máx}$:

$$
V_{GG2} < V_{DD} + V_{T0p} - n_p\phi_t(f(i_{f2})+4)
\tag{8}
$$

E para $V_{GG1}$:

$$
\frac{V_{GG1}-V_{DD}-V_{T0p}}{n_{n}}=-\phi_{t}f\left(i_{f1}\right)\\
V_{GG1} = V_{DD} + V_{T0p} - n_p\phi_{t}f\left(i_{f1}\right)
\tag{9}
$$

O procedimento pode ser resumido com o algoritmo a seguir:

<center>

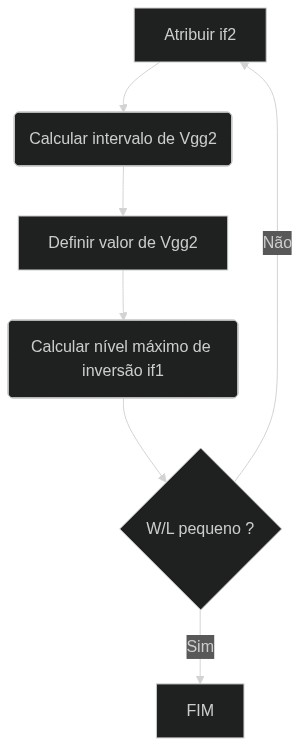[](https://mermaid.live/edit#pako:eNpNkE1OwzAQha9ieUWlVoguswChBCQkYFMEi6aLIZ6kI_wTXDsqSnIYxJpT5GLYadPi1djve2880_LCCOQJryzUW_aS5ZqFQ-VyfessvXuy8bJhi8U1a6pqSdpdpCALLyEo2qFtQBomkL0GdXawH8GTaZ1hSTpERdZO8OYMjySVVwr253Q9_DYomRq-96TGFqQbtLvhx0R2Nn01usaAtH27fGQ1fnrUht30ByCNWrci1bH7h6f_b88hqYvj8TlXaBWQCJtoI5Jzt0WFOU9CKcB-5DzXfeB8LcDhnSBnLE9KkDucc_DOrL50wRNnPU5QRhC2qo5U_wdk2Hf9)

</center>

O script responsável por esta simulação se encontra a seguir:

% Tensões de alimentação
VDD = 0.6;
VSS = -0.6;

% Parâmetros tecnológicos
VT0n = 0.3618;
VT0p = -0.3554;
nn = 1.3790;
np = 1.2952;
ISsqn = 353.38e-9;
ISsqp = 49.514e-9;
phit = 26e-3;

% Requisitos de projeto
Voutmax = 0.1;
Iout = 240e-6;

if2 = 36.814 # Ajuste manual

f_if2 = sqrt(if2+1)-2 + log(sqrt(if2+1)-1);

% Calculo de VGG2
Vgg2min = np*(Voutmax + 5*phit - ...
phit*log(sqrt(if2+1)-1)) - (np-1)*VDD + VT0p;
Vgg2max = VDD + VT0p - np*phit*(f_if2+4);
disp([num2str(Vgg2min),'V < Vgg2 < ',num2str(Vgg2max),'V']);
VGG2 = 0.9*Vgg2min+0.1*Vgg2max;
disp(['VGG2 escolhido: ', num2str(VGG2), 'V']);

% Calculo das correntes if
if1max = (-f_if2 - (VGG2-VDD-VT0p)/(phit*np) - 3).^2 -1
if1 = 0.9*if1max # Ajuste manual do peso

% Calculo de VGG1
VGG1 = VDD + VT0p - ...
np*phit*(sqrt(if1+1)-2 + log(sqrt(if1+1)-1))
VGG2

% Calculo das razoes de aspecto
W1_L1 = Iout./(ISsqp*if1)
W2_L2 = Iout./(ISsqp*if2)

% Calculo das dimensoes
L1=L2=0.2 # Arbitrado
L2
W1=L1*W1_L1
W2=L2*W2_L2

Os obtidos retornados pelo script:

>> fonte_cascode_octave

if2 =  36.814
-0.28981V < Vgg2 < -0.085019V
VGG2 escolhido: -0.26933V
if1max =  40.904
if1 =  36.813
VGG1 =  0.049684
VGG2 = -0.26933
W1_L1 =  131.67
W2_L2 =  131.66
L1 =  0.20000
L2 =  0.20000
W1 =  26.333
W2 =  26.333

## 2. Simulação do cascode calculado e ajuste empírico

A simulação destes valores realizada no software LTSpice, pode ser vista a seguir:

### 2.1. Esquemático:
<center>

<img src="https://i.imgur.com/5QHcZsS.png" width=480>

</center>

### 2.2. Gráfico $I_{out} \times V_{out}$

<center>

<img src="https://i.imgur.com/VDxO4RZ.png" width=480>

</center>

---

O valor de tensão $V_{GG1}$ foi ajustado para se obter a corrente de projeto $I_{OUT} = 240\mu A$ na metade da excursão de $V_{OUT}$.

$$
V_{GG1}=0.021V
$$

<center>


</center>

O ajuste foi realizado diminuindo $V_{GG1}$, pois como se trata de um transistor canal P, a diminuição em $V_{GG1}$ se reflete em um aumento em $V_{BG1}$, aumentando o nível de inversão e consequentemente o aumento da corrente $I_D$. Assim, segue-se para a próxima etapa, os circuitos divisores de tensão.

## 3. Dimensionamento dos transistores para os divisores de tensão.

A topologia de circuitos para geração de referência de tensão utilizada, está mostrada na imagem a seguir:

<center>


###### Figura 3 - Topologia divisor de tensão

</center>

Nesta topologia, a diferença de potencial entre fonte e substrato, nos dois transistores é nula. Assim:

$$
\begin{align}
V_{Pp} = \frac{V_{GBp}-V_{T0P}}{n_p}=-\phi_t f(i_f)\tag{canal P}\\
V_{Pn} = \frac{V_{GBn}-V_{T0N}}{n_n}=\phi_t f(i_f)\tag{canal N}\\
\end{align}
\tag{10}
$$

Por inspeção da figura $(3)$, é possível determinar a diferença de potencial entre porta e substrato para cada transistor:

$$
\begin{align}
V_{GBp}= V_X - V_{DD} \tag{canal P}\\
V_{GBp}= V_X - V_{SS} \tag{canal N}\\
\end{align}
\tag{11}
$$

Combinando as equações $(10)$ e $(11)$, e dos valores de $V_X$ determinados anteriormente, calculamos $f(i_f)$, a partir disso, determinamos a inversa aproximada da função para determinar os níveis de inversão $i_f$, para então calcular as razões de aspecto através de correntes $I_D$ escolhidas.

A função inversa foi obtida realizando uma regressão logarítimica através da expressão abaixo:

$$
f(i_f)\approx A\ln\left(B(i_f)^{C}+D\right)^{E}+F
\tag{12}
$$

Os pontos escolhidos atendem a região de inversão fraca, moderada e forte, até $i_f=250$ aproximadamente: $i_f=\left[0.1,0.15,0.2,...250\right]$. A função obtida foi:

$$
f_2(i_f)\approx39.2377\ln\left(-2.71958i_f^{0.0531707}+6.60001\right)^{-5.64938}-8.49241
\tag{13}
$$

A comparação com o gráfico real $\color{red}{f(i_f)}$ e a sua aproximação $\color{green}{f_2(i_f)}$ está mostrado abaixo:

<center>


</center>

A função $f_2(i_f)$ admite inversa, deste modo:

$$
i_f\approx\left(\frac{e^{\left(\frac{f(i_f)+8.49241}{39.2377}\right)^{\frac{1}{-5.64938}}}-6.60001}{-2.71958}\right)^{\frac{1}{0.0531707}}
\tag{14}
$$

Após determinar os níveis de inversão são escolhidos correntes $I_D$ para cada divisor de tensão, de modo que seja um valor menor possível (para economia de energia) em que ainda seja possível obter $\frac{W}{L}$ dentro dos limites de fabricação.

<center>

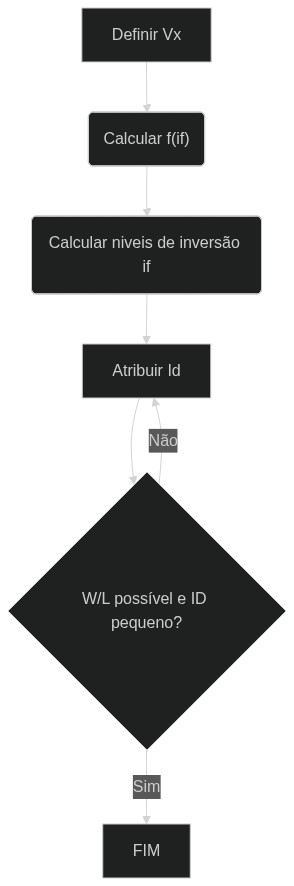[](https://mermaid.live/edit#pako:eNpNkE1OwzAQha8ymlUrtWLvBQglIEUCNkWwqCtk4jEdkdjBsaOiJKdhzSl6MZz-iVk9zfvePGl6LJ0mFPjhVbOF51xaSNPt1jkZtuzhZbeB5fIazBubmcRMVWWslAczYzOXOD8GJveAJeiCWO6IW9AEbDvy7f7HwRQ6JM68Xt8Gz-8xVRV6c_J0srL-9eoBGte2-9-OKiAocmjoK5J1N-MRzKYbw4rrAe6Lx_-7p1Q2pEO4wJp8rZIS2E-ExLClmiSKJLXynxKlHRMXG60C3WkOzqMwqmppgSoGt_q2JYrgI52hnFV6WH2ixj9-8mpa)

</center>

O script responsável por esta simulação se encontra a seguir:

% Tensões de alimentação
VDD = 0.6;
VSS = -0.6;

% Parâmetros tecnológicos
VT0n = 0.3618;
VT0p = -0.3554;
nn = 1.3790;
np = 1.2952;
ISsqn = 353.38e-9;
ISsqp = 49.514e-9;
phit = 26e-3;

% Valor das tensoes a serem obtidas
Vx = [0.021 -0.26933];

% Calculo do nível de inversão
f_if1 = (Vx-VSS-VT0n)/(nn*phit)
f_if2 = -(Vx-VDD-VT0p)/(np*phit)

if1 = ((e.^(((f_if1+8.49241)/39.2377).^(1/-5.64938))-6.60001)/(-2.71958)).^(1/0.0531707)
if2 = ((e.^(((f_if2+8.49241)/39.2377).^(1/-5.64938))-6.60001)/(-2.71958)).^(1/0.0531707)

% Escolha do I_D
Id = [12.3e-6 6.4e-6]; # Ajustado manualmente

% Calculo das razoes de aspecto
W1_L1 = Id./(ISsqn*if1)
W2_L2 = Id./(ISsqp*if2)

% Calculo das dimensoes
L1=L2=0.20 # Arbitrado
L2
W1=L1*W1_L1
W2=L2*W2_L2

Os obtidos retornados pelo script:

>> divisor_tensao_octave

f_if1 =

   7.22932  -0.86824

f_if2 =

    6.6399   15.2614

if1 =

   53.2078    1.6681

if2 =

    45.984   213.503

W1_L1 =

    0.65417   10.85686

W2_L2 =

   5.40214   0.60541

L1 =  0.20000
L2 =  0.20000
W1 =

   0.13083   2.17137

W2 =

   1.08043   0.12108

## 4. Simulação da rede de divisores de tensão e ajuste empírico

Com os valores determinados via script, foi realizada a simulação.

<center>


</center>

Os valores dos potenciais de porta estão na mesma ordem de grandeza que os valores esperados.

De acordo com a imagem anterior, foi ajustado o transistor **U3**, equivalente ao **M4** da figura $(1)$, o valor de $W$ foi ajustado:

$$
W_{M4} = 1.08\mu m \rightarrow 1.52\mu m
$$

Já na outra rede, o transistor ajustado foi o **U6**, equivalente ao **M5** da figura $(1)$:

$$
W_{M5} = 2.17\mu m \rightarrow 3.26\mu m
$$

Para aumentar o nível potencial $V_{GG1}$, foi realizado um aumento na razão de aspecto, através do aumento do comprimento $W_{M4}$. Deste modo, ocorre uma diminuição no nível de inversão deste transistor e assim, a tensão $V_{GB}$ diminui com a diminuição de $f(i_f)$ aumentando, neste transistor canal P, a tensão de porta $V_X$.

Já no ajuste do outro circuito divisor de tensão, foi necessário diminuir o valor de $V_X$ através do aumento da razão de aspecto no transistor canal N da topologia. Este aumento da razão de aspecto, através da dimensão de $W_{M5}$ ocasiona uma diminuição na inversão dese transistor, e por consequência uma menor tensão $V_{GB}$, ocasionando assim uma diminuição no nível de tensão.

Após os ajustes, temos finalmente as referências de tensão com os valores adequados:

<center>


</center>

## 5. Simulação da rede completa

Por fim, a simulação da rede completa é realizada:

<center>


</center>

<center>


</center>

Os resultados ficaram dentro do esperado, a rede completa fornece $240\mu A$ dentro dos limites conhecidos da carga $V_{out}<0.1V$.

## 6. Resultados do dimensionamento e das simulações

| Parâmetro | Valor |
| ------------------------------------------------------- |:--------:|
| $I_{OUT}$ ($\mu A$) especificada | 240 |
| $I_{OUT}$ ($\mu A$) calculados 2.1 | 183 |
| $I_{OUT}$ ($\mu A$) ajustados 2.2 | 240 |
| $I_{OUT}$ ($\mu A$) simulados 5.1 | 239.74 |
| $i_{f1}$ | 36.813 |
| $i_{f2}$ | 36.814 |
| $W_1 (\mu m)$ | 26.333 |
| $L_1 (\mu m)$ | 0.2 |
| $W_2 (\mu m)$ | 26.333 |
| $W_2 (\mu m)$ | 0.2 |
| $V_{GG1}$ ($V$) calculado | 0.0497 |
| $V_{GG1}$ ($V$) ajustado 2.2 | 0.021 |
| $V_{GG1}$ ($V$) simulado antes do ajuste do divisor 4.1 | -0.00527 |
| $V_{GG1}$ ($V$) simulado antes do ajuste do divisor 4.2 | 0.021046 |
| $V_{GG2}$ ($V$) calculado | -0.26933 |
| $V_{GG2}$ ($V$) ajustado 2.2 | -0.26933 |
| $V_{GG2}$ ($V$) simulado antes do ajuste do divisor 4.1 | -0.25541 |
| $V_{GG2}$ ($V$) simulado antes do ajuste do divisor 4.2 | -0.26997 |
| $W_3 (\mu m)$ calculado | 2.17 |
| $W_3 (\mu m)$ ajustado empiricamente | 3.26 |
| $L_3 (\mu m)$ calculado | 0.2 |
| $L_3 (\mu m)$ ajustado empiricamente | 0.2 |
| $W_4 (\mu m)$ calculado | 0.12 |
| $W_4 (\mu m)$ ajustado empiricamente | 0.12 |
| $L_4 (\mu m)$ calculado | 0.2 |
| $L_4 (\mu m)$ ajustado empiricamente | 0.2 |
| $W_5 (\mu m)$ calculado | 0.13 |
| $W_5 (\mu m)$ ajustado empiricamente | 0.13 |
| $L_5 (\mu m)$ calculado | 0.2 |
| $L_5 (\mu m)$ ajustado empiricamente | 0.2 |
| $W_6 (\mu m)$ calculado | 1.08 |
| $W_6 (\mu m)$ ajustado empiricamente | 1.52 |
| $L_6 (\mu m)$ calculado | 0.2 |
| $L_6 (\mu m)$ ajustado empiricamente | 0.2 |

<!--
https://tinyurl.com/yyw7m5cf
https://www.desmos.com/calculator/vrfzmjzpi2
https://www.desmos.com/calculator/tg1g77ebaa
-->

###### tags: `Eletrônica Analógica`