# Sin7Y Tech Review (21): Optimization of Multi-Scalar Multiplication Algorithm

Let $G$ be a cyclic group, $P_{i} \in G$ is the element in the group, $a_{i} \in \mathbb{Z}$ is the scalar, and the Multi-Scalar Multiplication (MSM) is the algorithm for calculating $\sum_{i=1}^{n} a_{i} P_{i}$ , the sum of multiple scalar multiplications. As the group operation is more complicated than the addition and multiplication of elements in the finite field, the MSM algorithm is employed to reduce the number of times of group operation as much as possible. Usually, $G$ is a cyclic group defined on the elliptic curve of $y^{2}=x^{3}+a x+b$ on the finite field of $\mathbb{F}_{p}$, with the order $|G|$ being $b \approx 256$ bits, and $0 \leq a_{i}<2^{b}$. If the group operation is conducted by the plain algorithm of fast exponentiation, the number of group operations needed for every $a_{i} P_{i}$ is $1.5 b n$ times on average, and for all $a_{i} P_{i}$ is $1.5 b$ times in total. Next, we will introduce some optimization methods corresponding to larger $n$.

## Optimization Based on the Windowing Technique
We can split the $b$ bit scalar into $c$ width windows: reduce the scalar to $2^{c}$ base system.

$$
a_{i}=a_{i, 0}+a_{i, 1} 2^{c}+a_{i, 2} 2^{2 c}+\cdots+a_{i, m-1} 2^{(m-1) c}
$$

where $m=b / c, 0 \leq a_{i, j}<2^{c}$.

Hence

$$
\begin{aligned}
a_{1} P_{1} &=a_{1,0} P_{1}+a_{1,1} 2^{c} P_{1}+\cdots+a_{1, m-1} 2^{(m-1) c} P_{1} \\
a_{2} P_{2} &=a_{2,0} P_{2}+a_{2,1} 2^{c} P_{2}+\cdots+a_{2, m-1} 2^{(m-1) c} P_{2} \\
& \cdots \\
a_{n} P_{n} &=a_{n, 0} P_{n}+a_{n, 1} 2^{c} P_{n}+\cdots+a_{n, m-1} 2^{(m-1) c} P_{n}
\end{aligned}
$$

so

$$
\begin{aligned}
\sum_{i=1}^{n} a_{i} P_{i} &=\sum_{i=1}^{n} \sum_{j=0}^{m-1} a_{i, j} 2^{j c} P_{i} \\
&=\sum_{j=0}^{m-1}\left(\sum_{i=1}^{n} a_{i, j} P_{i}\right) 2^{j c} \\
& \triangleq \sum_{j=0}^{m-1} Q_{j} 2^{j c}
\end{aligned}
$$

Here, $Q_{j}=\sum_{i=1}^{n} a_{i j} P_{i}$, so we reduce the original algorithm issue of $b$-bit MSM into a smaller $c$-bit issue. We can put the same scalars from $\sum_{i=1}^{n} a_{i j} P_{i}$ into a bucket and write them in another form:

$$
\sum_{i=1}^{n} a_{i j} P_{i}=\sum_{k=0}^{2^{c}-1} k \sum_{a_{i j}=k} P_{i}=\sum_{k=1}^{2^{c}-1} k S_{k}
$$

For example, when $c = 3$, it is calculated as:
$$
\begin{aligned}
Q_{j}=& 6 P_{1}+2 P_{2}+6 P_{3}+P_{4}+7 P_{5}+2 P_{6}+3 P_{7} \\
&+5 P_{8}+P_{9}+4 P_{10}+6 P_{11}+7 P_{12}+3 P_{13}+P_{14} \\
=&\left(P_{4}+P_{9}+P_{14}\right) \\
&+2\left(P_{2}+P_{6}\right) \\
&+3\left(P_{7}+P_{13}\right) \\
&+4 P_{10} \\
&+5 P_{8} \\
&+6\left(P_{1}+P_{3}+P_{11}\right) \\
&+7\left(P_{5}+P_{12}\right) \\
=& S_{1}+2 S_{2}+3 S_{3}+4 S_{4}+5 S_{5}+6 S_{6}+7 S_{7}
\end{aligned}
$$

When calculating $\sum k S_{k}$, set the partial sum $T_{l}=S_{l}+\cdots+S_{k}$, then

$$
Q_{j}=\sum_{k=1}^{2^{c}-1} k S_{k}=\sum_{k=1}^{2^{c}-1} \sum_{l=k}^{2^{c}-1} S_{l}=\sum_{k=1}^{2^{c}-1} T_{k}
$$

However, the operation results of $T_{l}$ can be obtained through the recurrence sequence $T_{l}=T_{l+1}+S_{l}$. It means that only one group operation is needed for the operation for each $T_{l}$. Under the MSM algorithm with $c$-bit scalar, all $S_{k}$ requires $n-2^{c}+1$ times of group operation. All $T_{k}$ requires $2^{c}-1$ times and the sum of these $T_{k}$ requires $2^{c}-2$ times of group operation. Therefore, each window with the value of $c$ requires $n+2^{c}-2$ times of group operations. The operation of $\sum_{j=0}^{b / c-1} Q_{j} 2^{j c}$ only requires the normal method of fast exponentiation by ($(b / c-1)(c+1)=b-c+b / c-1$ times of group operation.

In summary, we can conclude that the total number of group operations required by the method of the Windowing Technique of a width of $c$ is
$$
\frac{b}{c}\left(n+2^{c}-2\right)+b-c+\frac{b}{c}-1 \approx \frac{b}{c}\left(n+2^{c}\right)
$$

Set $c=\log n$, then the number of group operations is $2 b n / \log n$. When $n \approx 10^{5}$ , the number of group operations reduces to $1 / 12$ of its original value.

## Optimization Based on Group Endomorphism
For the cyclic group $G$ on the elliptic curve $y^{2}=x^{3}+a x+b$ on the finite field $\mathbb{F}_{p}$ , if the following group endomorphism of $\varphi$ can be found: there exists $\alpha, \beta \in \mathbb{F}_{p}$, satisfying $\varphi(x, y)=(\alpha x, \beta y)$ holds for all the points on $G$, then it is easy to prove that such an endomorphism is a multiplication map, namely there is a $\lambda$ making $\varphi(P)=\lambda P$ hold for all the points of $P$ on $G$, which means that whenever we know the coordinates of one point, we can change it to the coordinates of another point simply by multiplying a number in $\mathbb{F}_{p}$ to both the values of abscissa and ordinate. The algorithm can be further optimized based on this important property.

When $\lambda=-1$, $\alpha=1, \beta=-1$. The reverse value of one point can be obtained only by taking the opposite number from the ordinate. Based on this feature, in the plain fast exponentiation algorithm, the scalar can be written into the non-adjacent form (NAF), namely $\sum e_{i} 2^{i}, e_{i} \in\{-1,0,1\}$ and any two adjacent $e_{i}$ cannot be non-zero at the same time. Compared to the $b$-bit scalars, the group operation number in the fast exponentiation algorithm can be reduced from the original average of $3 / 2 \cdot b$ times to $4 / 3 \cdot b$ times. This technique can also be used to optimize the Windowing Technique. After writing $a_{i}$ to $a_{i}=\sum_{j=0}^{b / c-1} a_{i, j} 2^{j c}, 0 \leq a_{i, j}<2^{c}$, conduct the following operation:

The result of $a_{i}=\sum_{j=0}^{b / c-1} a_{i, j}^{\prime} 2^{j c}$ and$-2^{c-1} \leq a_{i, j}^{\prime} \leq 2^{c-1}$ can be obtained. Since the complexity of addition and subtraction in group operation of an elliptic curve is the same, we can put these terms into a bucket according to the absolute value of scalars. Therefore, the number of groups can be reduced from the original 2c to $2^{c}$ , and the overall number of group operations required is reduced from (1) to:

$$
\frac{b}{c}\left(n+2^{c-1}\right)=\frac{b}{c^{\prime}+1}\left(n+2^{c^{\prime}}\right)
$$

If the parameters of the elliptic curve are special, for example, the BLS curve can be written as $y^{2}=x^{3}+b$, and $p \equiv 1(\bmod 3)$, take third-order element $\alpha$ from $\mathbb{F}_{p}^{\times}$, then there is a corresponding $\lambda$ that holds $\lambda(x, y)=(\alpha x, y)$


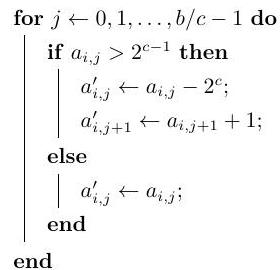
Algorithm 1: Signed Digits

In addition, $\lambda^{3} \equiv 1(\bmod |G|)$. Then the multiplication operation can be optimized as follows:
$$
\begin{aligned}
m P &=\left(m_{1}+m_{2} \lambda\right) P \\
&=m_{1} P+m_{2}(\lambda P) \\
&=m_{1} P+m_{2} \varphi(P)
\end{aligned}
$$

From [1], we can find a small enough scalar $\left|m_{1}\right|,\left|m_{2}\right|<\sqrt{G}$ to make the above equation true, which gives us a way to reduce the multiplication of $b$ bits into the multiplication of two $b / 2$ bits. Use it into the Windowing Technique, and the number of group operations is reduced to

$$
\frac{b / 2}{c}\left(2 n+2^{c}\right)=\frac{b}{c}\left(n+2^{c-1}\right)=\frac{b}{c^{\prime}+1}\left(n+2^{c^{\prime}}\right)
$$

In summary, both the above two optimization methods can reduce the number of group operations by $5.5 \%$ when $n=10^{5}$.

## References
[1] Francesco Sica, Mathieu Ciet, and Jean-Jacques Quisquater. Analysis of the gallant-lambert-vanstone method based on efficient endomorphisms: Elliptic and hyperelliptic curves. In International Workshop on Selected Areas in Cryptography, pages 21–36. Springer, 2002.