# Big O Notation
A way to evaluate the time and space **complexity** of an algorithm
---
## Space complexity
*How much space (memory) an algorithm uses to run, as a function of the input size.*
1. find all the variables (incl arrays, structs)
2. sum up their size, wrt the input size $n$ *if possible*
3. remove constants
4. give a small upper bound ($\mathcal{O}$ notation) (take the largest element)
Idea of "small upper bound": the time / space complexity **does not exceed** the bound.
---
```c
int main() {
int a = 3;
int b = 2;
int c = 1;
printf("%d\n", a - b - c)
}
```
1. find all the variables: `a`, `b`, `c`
2. sum up their size, wrt the input size $n$ *if possible*: `1`+`1`+`1` = `3*1`
3. remove constants: removing `3` gives us `1`
4. give a small upper bound ($\mathcal{O}$ notation) (take the largest element): `O(1)`
---
```c
int sumArray(int[] array, int size) {
int sum = 0;
for (int i = 0; i < size; i++) {
sum += array[i];
}
return sum;
}
```
1. find all the variables: `array`, `size`, `sum`, `i`
2. sum up their size, wrt the input size $n$ *if possible*: `n`+`1`+`1` + `1` = `n + 3*1`
3. remove constants: `n + 1`
4. give a small upper bound ($\mathcal{O}$ notation) (take the largest element): `O(n)`
---
## Time complexity
*How much time an algorithm takes to run, as a function of the input size*
1. find all **elementary operations** performed
2. sum up the time taken to execute each
3. remove consants
4. Give a small upper bound ($\mathcal{O}$ notation) (take the largest element)
Idea of "small upper bound": the time / space complexity **does not exceed** the bound.
---
## Elementary operation
A statement or bounded part of the code
Examples:
- Comparisons
- Swap
- Array indexing
- Assignment
- A Math operation (divide, add)
If an elementry operation exists inside another, multiple their complexities to get the complexity of that bit of code
---
```c
int sumArray(int[] array, int size) {
int sum = 0; <-- elementary operation (eo)
for (int i = 0; i < size; i++) { <---|
sum += array[i]; <-- eo | eo
} <---|
return sum;
}
```
1. find all **elementary operations** performed: Marked above
2. sum up the time taken to execute each: `1` + `n * 1` + `1` = `n + 2*1`
3. remove consants: `n + 1`
4. give a small upper bound ($\mathcal{O}$ notation) (take the largest element): `O(n)`
---
```c
int sumArray(int[] array, int size) {
int sum = 0; <-- elementary operation (eo)
for (int i = 0; i < size; i++) { <---|
sum += array[i]; <-- eo | eo
} <---|
return sum; <-- elementary operation
}
```
Here the time and space complexity of the algorithm is the same, but **this is not always the case**
---
```c
void sumArray(int[] array, int size) {
int sum = 0; <-- eo
for (int i = 0; i < size; i++) { <--|
for (int j = 0; j < size, j++) { <--| |
if (i != j && array[i] == array[j]) { <-- | | |
printf("Match found!\n"); |eo |eo |eo
} <--| | |
} <--| |
} <--|
}
```
1. find all **elementary operations** performed: Marked above
2. sum up the time taken to execute each: `1` + `n*n*1` = `n^2 + 1`
3. remove consants: `n^2 + 1`
4. Give a small upper bound ($\mathcal{O}$ notation) (take the largest element): `O(n^2)`
What is the space complexity of this algorithm?
---
## Why Big O?
$$T(n) \approx c_{op} \times C(n)$$
- $T(n)$: Running time
- $c_{op}$: Cost of elementary operation
- $C(n)$: number of elementary operations executed
- $n$ input size (can have multiple variables though)
---
$$T(n) \approx c_{op} \times C(n)$$
$c_{op}$ is going to depend on the computer you're running the algorithm on, we want our cost estimate to be **agnostic** of the machine we are running on.
Set $c_{op} = 1$ (elementary operation has unit size).
$$T(n) \propto C(n)$$
---
Time complexity can be one of the following:
Constant: **O(1)**
Logarithmic: **O(log n)**
Linear: **O(n)**
Superlinear: **O(n log n)**
Quadratic: **O(n^2)**
Cubic: **O(n^3)**
Exponential: **O(2^n)**
Factorial: **O(n!)**
(rare): **O(n^n)**
These are in accending order
---
Make sure you can recognise the following (at minimum):
---
### O(1)
```c
printf("Hello!")
```
---
### O(log n)
```c
while (x > 0) {
x = x / 2;
}
```
Generally, if an input reduces by half each iteration, the time complexity is O(log n)
---
### O(n)
```c
for (int i = 0; i < n; i++) {
printf("%d\n", n);
}
```
---
### O(n log n)
```c
for (int i = 0; i < n; i++){
for(int j = 0; j < n; j = j * 2) {
printf("Hey - I'm busy looking at: %d and %d\n", i, j);
}
}
```
---
### O(n^2)
```c
for (int i = 0; i < n; i++){
for(int j = 0; j < n; j = j++) {
printf("Hey - I'm busy looking at: %d and %d\n", i, j);
}
}
```
---
Remember to take the largest complexity of an algorithm...

$T_1(n) = 12n^2$ is the biggest....
---
## Search algorithms
AIM: Go through a search area (an array, possible solutions) to find a target.
Main solutions:
- Linear (sequential) search
- Binary search
---
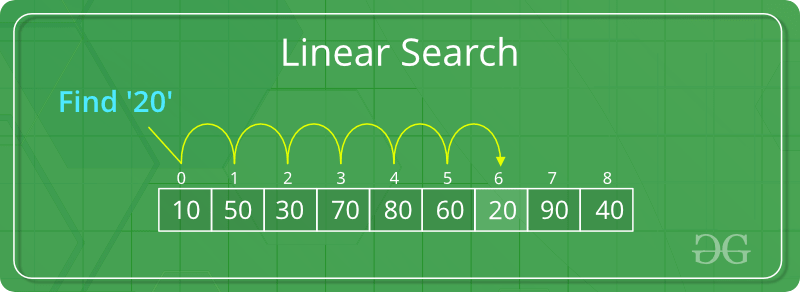
## Linear Search
Idea: Iterate one-by-one through the search space, checking if the target matches.
---
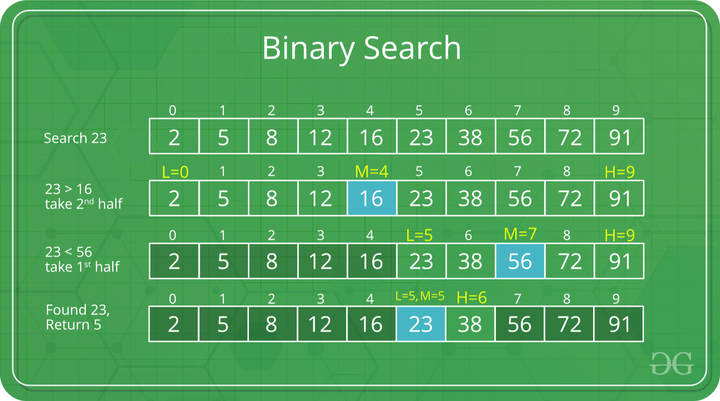
## Binary Search
Idea: Repeatedly divide the search interval by half.
Important: Only works for a **sorted** search space (array), and elements must support **order** operations (<, >)
---
Essentially all we are doing is splitting the array into two recursively...
---
## Best, Worst and Average Cases
Analysing the **performance** of an algorithm, we often consider the **best**, **worst** and **average** cases of running them.
For the average case, usually probability is involved (how likely is any permutation of an input to occur)? It's **NOT** the average of the best and worst cases
---
### Linear Search
Best Case: Find element on first comparison ie. element is first in the array
Worst Case: Element does not exist in the arry
Average Case: Element exists however it is not first
**What are the time complexity of these?**
Best Case: O(1) <!-- .element: class="fragment" data-fragment-index="1" -->
Worst Case: O(n) <!-- .element: class="fragment" data-fragment-index="1" -->
Average Case: O(n) <!-- .element: class="fragment" data-fragment-index="1" -->
---
### Binary Search
Best Case: Find element on first comparison ie. element is in the middle of the array
Worst Case: Element does not exist in the arry
Average Case: Element exists however it is not in the middle
**What are the time complexity of these?**
Best Case: O(1) <!-- .element: class="fragment" data-fragment-index="1" -->
Worst Case: O(log n) <!-- .element: class="fragment" data-fragment-index="1" -->
Average Case: O(log n) <!-- .element: class="fragment" data-fragment-index="1" -->
---
## Quick Sort
1. Choose a pivot
2. Put everything that is less than the pivot to the left side of the array
3. Put everything that is greater than the pivot into the right side of the array
4. Put the pivot into the middle
5. Repeat steps 1 - 4 on each new array until sorted
---

---
### Choosing a Pivot...
Choosing a pivot can significantly effect the time the algorithm takes to execute
Slides here to go through in your own time: https://docs.google.com/presentation/d/1QXckJIliJC3PKcDQhF8d0pH4-KDttKZqFnA9-mehgIU/edit?usp=sharing
---
### Time Complexity of QuickSort
What do we know?
1. We have to look at every element at least once
2. The number of times we look at the elements again depends on the pivot
Based on these two points we know that quick sort will be O(n * number of times we look at an element again)
---
**Best Case:** We look at the elements log(n) times again
**Worst Case:** We look at all the elements n times again
**Average Case:** We look at the elements log(n) times again
Resource for visualising this: https://iq.opengenus.org/time-and-space-complexity-of-quick-sort/
Therefore, the time complexity is **O(n log n)** in Best and Average case and **O(n^2)** in Worst case
---