The Required Serenity Active Validator Yield Model
Based on the variables that impact efficient validators' yield expectations, we introduce the Required Serenity Active Validator Yield model (RSAVY), a multivariable capital asset pricing model for determining the required rate of return for capital efficient validators. The RSAVY model is a risk-weighted pricing formula that takes into account the following return requirements and risk factors:
- The opportunity cost of allocating capital to a risk free rate
- The cost of illiquidity of ETH2
- The opportunity cost of investing in the underlying asset's benchmark
- The opportunity cost of lending the asset
- The discount/premium of the derivative asset
- The cost of validating
- The cost of penalties
- The cost of being slashed
Expressed mathematically, we obtain:
$$
R_v=R_f+\frac{C i T}{\max (1, T-t)}+\left(\beta_b-1\right)\left(R_{b m}-C_{b m i}-R_f\right)+D_a+\beta_d\left(R_{d m}\right)+C_y+P_p\left(\frac{N p}{S}\right)+P_s\left(\frac{N s}{S}\right)+\alpha_v
$$
Where:
- $R_v=$ revenue yield of validator
- $R_f=$ risk free rate
- $C_{i T}=$ cost of illiquidity at time $T$ (i.e. the spread at end of investment), or $\frac{P a-P b}{(P a+P b / 2}$ where $P a=$ price of ask and $P b=$ price of bid at time $T$, which is divided by the maximum of 1 or the expected holding period (in years)
- $\beta_b=$ beta, or $\frac{\operatorname{Covar}(R b, R e)}{\operatorname{Var}(R b)}$, of the returns of the staked asset and its benchmark (e.g. Bitcoin and Ether, respectively), minus one to account for the difference in volatility risk between the assets
- $R_{b m}=$ expected return of underlying asset benchmark, e.g. Bitcoin
- $C_{b m i}=$ cost of illiquidity of underlying asset benchmark at time $T$
- $D_a=$ discount (negative value) / premium (positive value) of the derivative, if applicable
- $\beta_d=$ yield beta of returns of lending opportunity cost, such as a DeFi benchmark, against average network validator net returns; yield beta is the slope of a plot of the benchmark's yields and the underlying asset's yields
- $R_{d m}=$ expected return on DeFi benchmark
- $C_y=$ the cost of validating

---

## Gas Cartel Attack


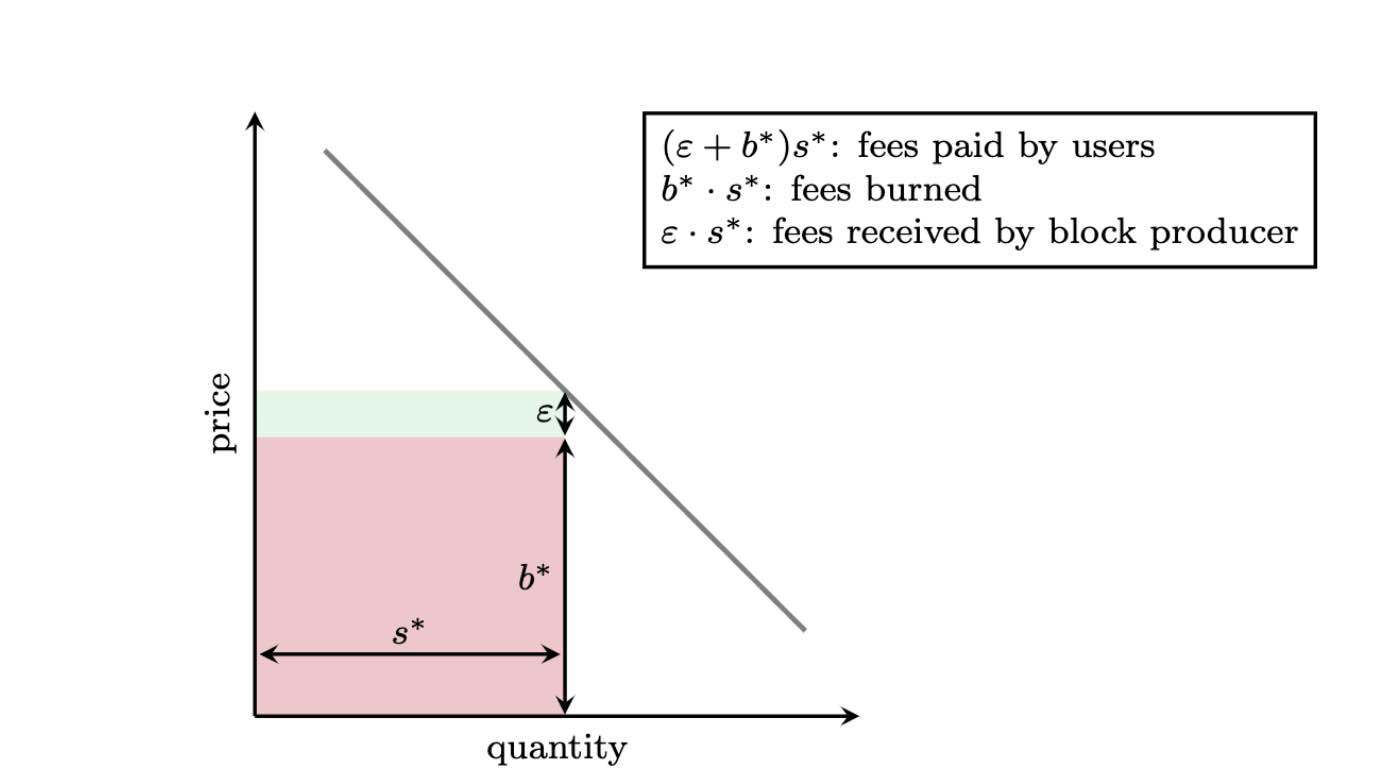
Figure 1: Demand curve for Ethereum transactions. The quantity ( $x$-axis) indicates the number of the transactions willing to pay the transaction fee (price shown $y$-axis). In steady state, $s^*$ transactions are willing to $b^*+\varepsilon$, where $b^*$ is the base fee that corresponds to the target size. The red area is the amount of fees being burned, whereas the blue area are the fees received by the miner.


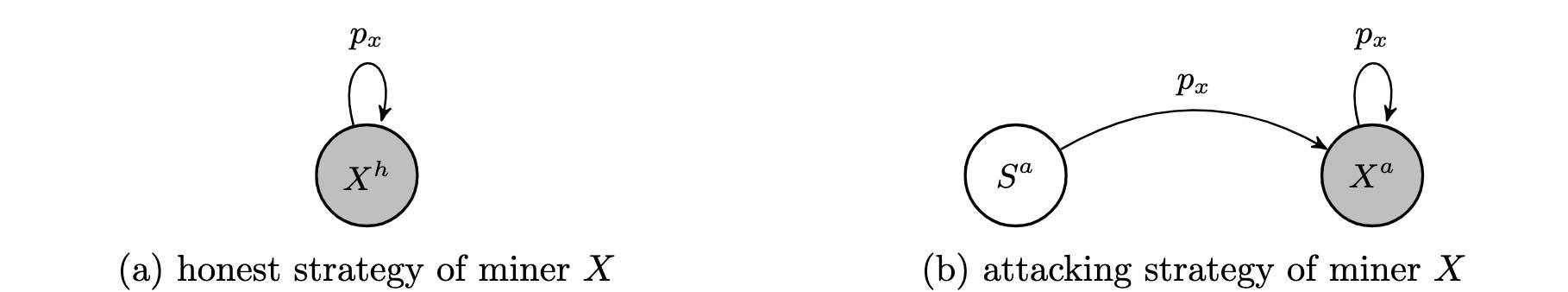
The starting point for the attack, denoted as state $S^a$, is when miner $X$ submits an empty block. Therefore, the payout in state $S^a$ is 0 . But with a probability of $p_x$, miner $X$ is chosen as the proposer for the next block and enters state $X^a$, where it submits a block at the target size. The payout in state $X^a$ can be calculated by
$$
P\left[X^a\right]=s^*\left(\phi \cdot b^*+(1-\alpha) \varepsilon\right) .
$$

Thus, as individual Ethereum pools control in excess
of 20% of the mining (staking) power


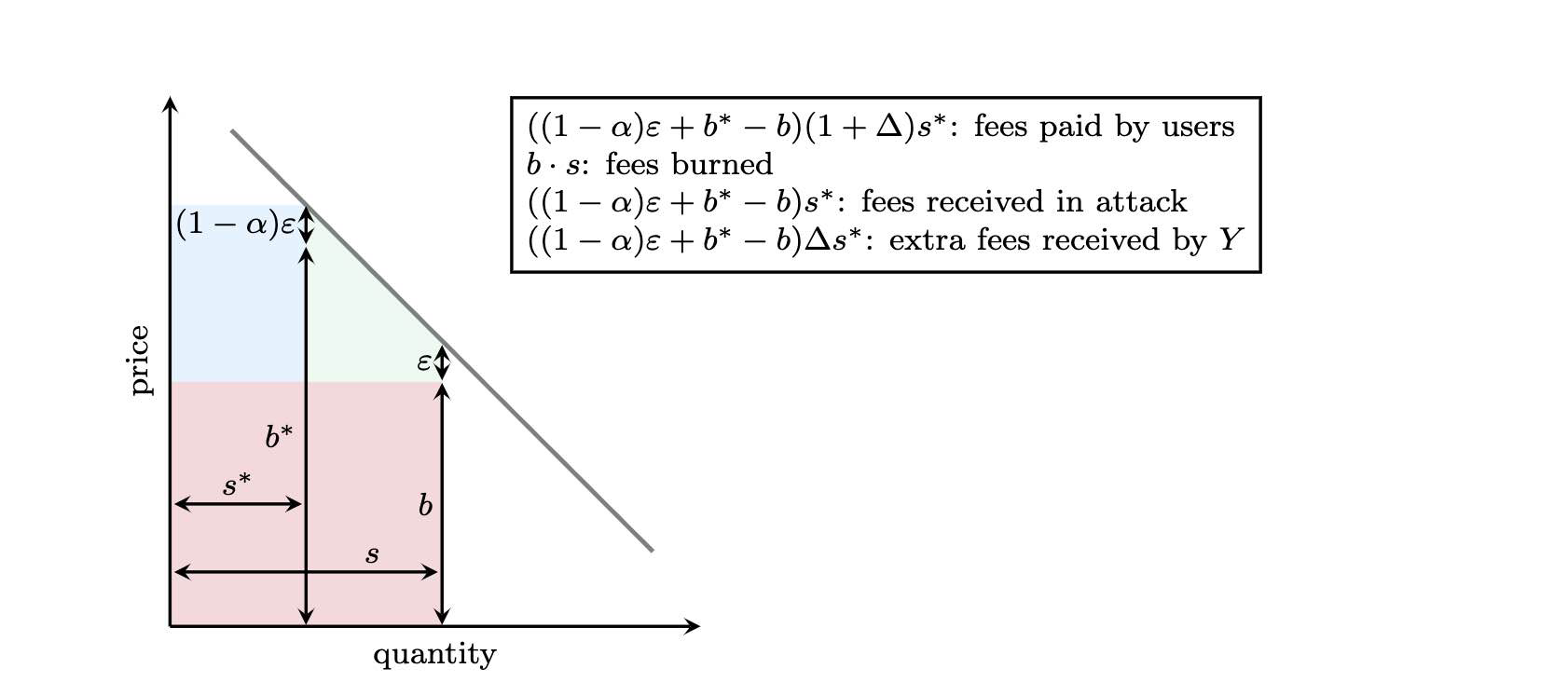
Figure 4: Demand curve for Ethereum transactions. The quantity ( $x$-axis) indicates the number of the transactions willing to pay the transaction fee (price shown $y$-axis). In steady state, we are at point $\left(s^*, b^*\right)$ on the demand curve. In case, the base fee was lowered to $b<b^*$, the demand is increased to $s \geq s^*$. An honest miner that will fill up the block with all transactions, paying at least the base fee. The red area indicates the amount of fees being burned, the blue area the fees the attacking miner $X$ received and the green area are the additional fees received by the honest miner $Y$ for including all transactions.

---

### Lending Markets

There are two common transaction reordering attacks on lending platforms utilizing fixed spread liquidations. In the first attack, the attacker observes an upcoming oracle update that will make a loan available for liquidation and back-runs (cf. Figure 1d) the corresponding transaction. The attacker wants to place its transaction immediately after the oracle update transaction to be first to claim the discount. Additionally, an attacker might observe a liquidator attempting a profitable liquidation in the mempool and perform a fatal front-running transaction (cf. Figure $1 b$ ) to steal the associated profit.

Market structure
Allocation mechanism
Relays are "brokers"
Whole block auction: The proposer sells off their entire rights to make a block.
- Relay expected to guarantee
validity of the good
Highest bid selected by mev-boost.
- Relay could fail
- Submit an invalid block
- Pay proposer less than promised
- Deliver late/not at all