---
tags: 225-spr22, specs
---

# Standards for Assessments in MTH 225

This document contains all the details for what constitutes "successful" or "acceptable" work on each type of assignment in the course. Use the table of contents in the upper-left to navigate to specific assignment types.

## Daily Prep

Daily Prep assignments are graded on the basis of **completeness and good-faith effort**. Correctness is not taken into account; but a good-faith effort to *try* to be correct must be evident. A mark of `1` is recorded for a Daily Prep on Blackboard if the work meets the standards; a mark of `0` is recorded otherwise.

| The work receives a mark of... | If it meets these criteria: |
| :----: | ---- |
| **1** | <ul><li>The assignment is submitted by the deadline, *and*</li><li>Every item on the response form has a response, *and*</li><li>There is at least one substantive question, comment, or comment reply on Perusall for either the text or a video</li></ul>
| **0** | One or more of the standards is not met: The assignment is late; or there is an item on the response form that is blank (even if by accident); or there is no substantive engagement with the reading and viewing on Perusall. |

## Learning Targets

There are three different ways to demonstrate skill on a Learning Target: By working a problem on a Learning Target quizzes, by working a problem in an oral quiz in drop-in hours, and by working a problem recorded to a Flipgrid video.

Both **written and oral quizzes** are graded on the basis of *completeness and correctness*. A mark of `Successful` is recorded for a Daily Prep on Blackboard if the work meets the standards; a mark of `Retry` is recorded otherwise.

| The work receives a mark of... | If it meets these criteria: |
| :----: | ---- |
| **Successful** | <ul><li>Each part of the problem has a good-faith attempt at a response, *and*</li><li>The response contains **no more than two simple errors**, and **no non-simple errors**, *and*</li><li>Unless specifically stated otherwise, the response must show all the significant steps used to arrive at the answers.</li></ul>
| **Retry** | Not all the standards for "Successful" are met. |

**Note:** The above are *general* criteria for successful demonstrations of skill on a quiz problem. Some quiz problems may have different or more targeted criteria that will be clearly stated on the quiz.

:::info
**What is a "simple error"?** For MTH 225, a "simple" error is defined to be *an error in logic, computation, or communication that does not pertain to the learning target and does not oversimplify the problem*.

For example, if you are adding `1011` and `1111` together in binary, and you miscopy the first number as `1101` and then go on to do the addition correctly, this is considered a "simple error" because it doesn't show evidence of an issue with your understanding of the Learning Target (because you did the addition correctly) and it didn't simplify the problem to make it easier.

However, if you are doing the same problem and "miscopy" the first number as `0000`, then that is **not** a simple error because it makes the addition problem trivial --- the problem is no longer a legitimate source of information about your ability to add numbers in binary.

Or, if you copy everything down correctly and add `1011` and `1111` but get an answer of `0100` even while showing your work, that's almost certainly a **non-simple** error that comes from misunderstanding how binary addition works. (You get `0100` if you [XOR](https://mathworld.wolfram.com/XOR.html) the bits together, but proper binary addition would give an answer of `11010`.)

Note that **an error that is considered "simple" in one situation may be "non-simple" in another**. For example, Learning Targets 12 and 15 both involve [the factorial function](https://en.wikipedia.org/wiki/Factorial). Making an error in computing this function, for example computing $10! = 1000$, would be *non-simple* for Learning Target 12 since the entire target is about computing these functions correctly; but might be "simple" in Learning Target 15 since this target is not about computing factorials but whether you can apply factorials to solving counting problems. Using the factorial in the right way but messing up the computation does not necessarily mean you haven't successfully demonstrated skill on that target.

**But keep in mind that only two simple errors are allowed on any Learning Target problem.** Having three or more simple errors indicates that a retry is in order to apply more careful attention to the attempt. So **always double-check your work when possible**, and **proofread your solutions before submitting them**.

:::

**Video solutions** are graded similarly to written and oral quizzes, but there is an additional criterion for *technical quality* of the video:

| The work receives a mark of... | If it meets these criteria: |
| :----: | ---- |
| **Successful** | <ul><li>All the standards for "Successful" shown above are met, *and*</li><li>The video is less than 5 minutes in length, *and*</li><li>Your face, voice, and handwriting are simultaneously in the frame at all times, *and*</li><li>The handwriting is legible and both the video and audio are clear.</li></ul>
| **Retry** | Not all the standards for "Successful" are met. |

## AEPs

AEP solutions are graded on the basis of *completeness, correctness, and communication quality*. Solutions are marked using the **EMRN rubric** shown below.


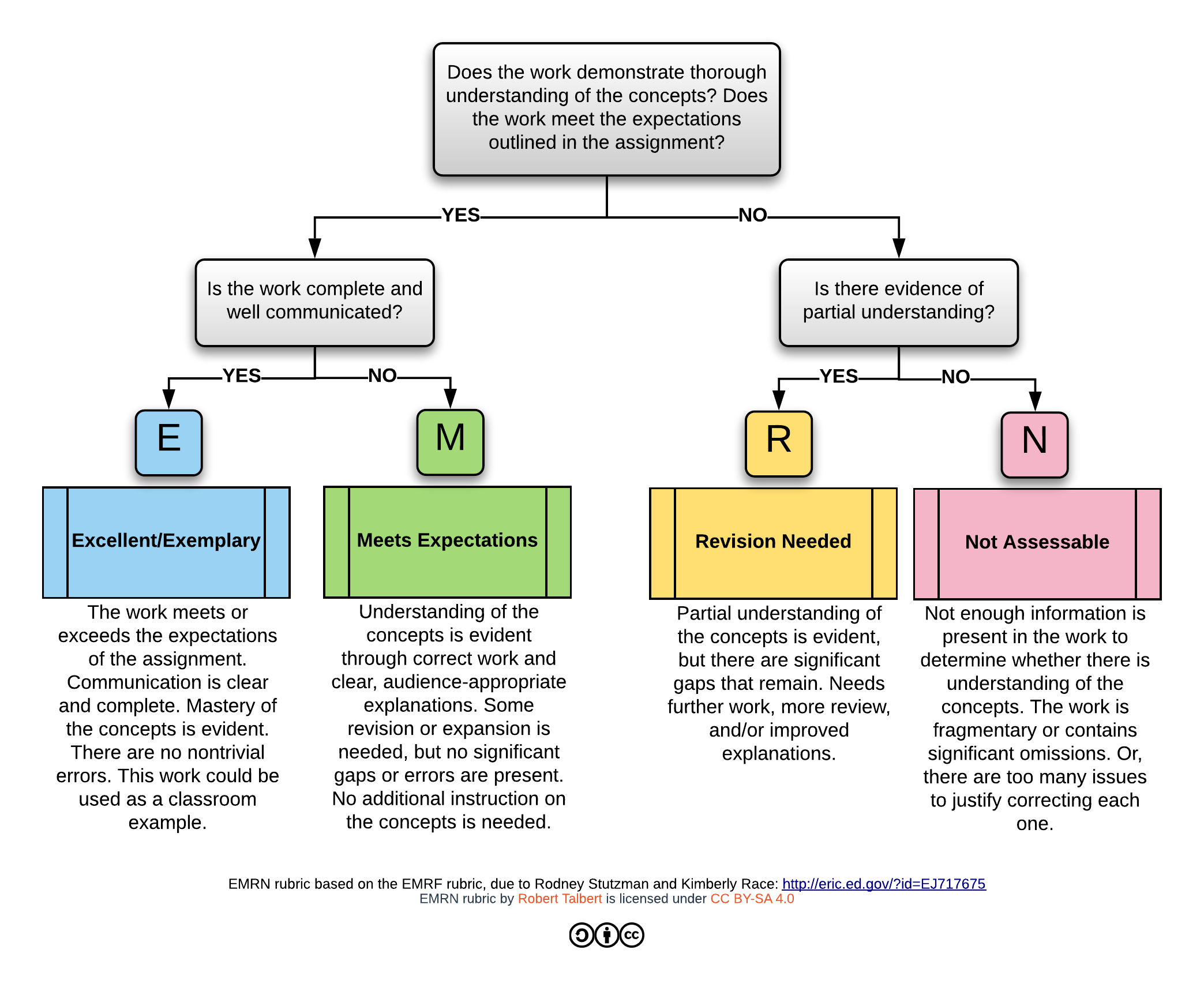
### Specific requirements for "Meets Expectations"

:::info
Note: **The audience for all AEP solutions is your classmates** --- people who have the background mathematical knowledge that you have, but who have no familiarity with the problem you are working on. **Prof. Talbert is not the audience, and neither are you** --- so don't assume that the person reading the solution has a Ph.D. or has been studying the problem for a while.
:::

For an AEP solution to "Meet Expectations", it must:

- **Obey fundamental rules of English usage** such as correct spelling, proper use of punctuation, use of complete sentences and proper paragraph structure, and so on.
- **Be mathematically correct and include no significant errors.** Note that *minor* errors can sometimes be acceptable as long as they don't derail the solution; for example a sign error in a mathematical computation *might* be insignificant in some cases. You should always proofread your work to debug those errors, because sometimes an error that is minor in one context is significant in another.
- **Give not just an answer but a full, convincing, and well-reasoned argument**. The answer is not being graded (and some AEPs may not have single right answers) --- **the thought process is what is being graded.**
- **Present a solution that thoughtfully combines mathematics and verbal explanations to be clear and convincing to the intended audience.** When giving a mathematical solution, don't just present a "wall of math" --- nothing but equations with no verbal description. Likewise, don't just talk about the solution without using any math. Instead, use a combination of words and math that explains your ideas clearly to a standard audience.
- **Define all mathematical objects that are being used**. This includes stating all assumptions in concrete terms, stating what a variable represents if you introduce one, and explaining how to construct or create any new objects before you use them.
- **Use proper mathematical notation and terminology and writing style**. For example if you want to write "x squared", type $x^2$ and not `x^2`. The use of plain text formatting of mathematical notation will result in the work being marked `R` and will require a revision. Use the equation editor found in your favorite word processor; ask for help or alternative tools if needed.

### Specific requirements for "Excellent/Exemplary"

An exemplary solution must first meet all objectives listed for "Meets Expectations". In addition, your work must also be very well communicated. There are many ways to do this: Here are some things to focus on:

* **Demonstrate fluency and comfort with the ideas in your solution**. Show that you fully understand what matters (and what doesn’t) in your solution, and how to properly use all terminology and ideas.
* **Write concisely and elegantly**. Find the most direct, clear, and unambiguous way to say what you mean. Avoid irrelevant flourishes or details. If you find a complex solution that requires many cases or a page of gnarly computations, perhaps there is a simpler way to do it -- find that simpler approach.

### Criteria for "Not Assessable"

An AEP submission is marked `N` (Not Assessable) if it does not represent a good-faith effort to meet the standards. This mark will be given in *any* of these circumstances:

- **Part of the solution is blank, partially complete, or contains insignificant attempts at a solution**. For example, completing part of a problem and then explaining that you didn't know how to complete the other parts will result in an`N`.
- There are **significant and numerous major errors** or misconceptions on mathematics or logic that occur throughout the work.
- **The submission is significantly disorganized, illegible, messy, or unprofessionally written up**. In particular, all AEP solutions must be typed; handwritten work will be automatically marked `N`.

AEP solutions that are marked `N` will be marked and returned without feedback (except for an explanation why it was marked `N`). You may revise an AEP marked `N`, but **only three such revisions are allowed during the semester**. All `N` solutions after the third one are ineligible for revision.

## Online Practice

Online Practice exercises are auto-graded on WeBWorK on the basis of *correctness only*. Each WeBWorK problem is worth 1 point, which is awarded if (and only if) the answer is correct. Partial credit is sometimes awarded on an exercise if it has multiple parts.