# 03 Statistika - CZ (8h)
###### tags: `řsss-základ`, `matika`, `mv013`
> Statistika. Popisná statistika (charakteristiky polohy a variability, pořádkové statistiky, statistiky asociace, související grafy). Diskrétní a spojité náhodné veličiny (NV). Náhodný výběr. Parametrické pravděpodobnostní modely (distribuce) NV. Centrální limitní věta. Princip věrohodnosti, bodové a intervalové odhady. Statistická inference - testování hypotéz, hladina významnosti, koeficient spolehlivosti. Testování hypotéz na jednom vzorku, dvou vzorcích, více než dvou vzorcích (včetně jednovýběrových, dvouvýběrových a párových t-testů, ANOVA a post-hoc testů), testů dobré shody. Lineární regresní model. (MV013)
---
:::success
**Vzorce** a **formální definice**.
:::
> **Vzorce** a **definice**
> [color=green]
:::info
**Volné definice** a **vysvětlení**.
:::
> **Vysvetlenie**
> [color=#0047AB]
> **Príklad**
> [color=purple]
:::warning
:book: Zdroj, další zdroje na přečtení
:::
<style>
blockquote span {color:#333;}
blockquote blockquote span {color:#333;}
span.color.fa-tag {display: none;}
</style>
Takto `*[MV013]` sú označené pojmy, ktoré nie sú v zadaní otázky, no preberali sa na MV013 a môžu sa zísť.
---
> Disclaimer: poznámky sú z veľkej miery prevzaté z [materiálov](https://hackmd.io/@uizd-suui/ryQrtIvzU) vypracovaných študentami umelej inteligencie a spracovania dát na podzim 2020.
---
:::info
**Statistika** je vědní obor, který se zabývá sběrem, organizací, analýzou, interpretací a prezentací empirických dat za účelem prohloubení znalostí určité oblasti, obvykle hromadného jevu.
:::
## Popisná štatistika
:::info
**Popisná statistika** je **statistika**, která kvantitatívně popisuje nebo sumarizuje vlastnosti nějaké sady dat, zatímco popisná statistika představuje **proces** používání a analýzy těchto popisných statistik
:::
:::info
:bulb: Popisná statistika se od **infereční statistiky** liší cílem **shrnout, resp. popsat** vzorek dat **namísto odvodzování poznatků** o populaci, kterou reprezentuje daný vzorek.
:::
**Typy proměnných**
- číselné
- kategorické
- nominální (neexistuje uspořádání), např. barva očí, pohlaví, bydliště...
- ordinálne (existuje uspořádání), např. známka ve škole, dosažené vzdělání
> _Má zmysel daná charakteristika pre daný typ premennej?_
>
> | charakteristika | číselná | nominálna | ordinálna |
> | --------------- | ------- | --------- | --------- |
> | priemer | :heavy_check_mark: | :x: | :x: |
> | medián | :heavy_check_mark: | :x: | |
> | modus | :heavy_check_mark: | :heavy_check_mark: | :heavy_check_mark: |
> | kvantil | :heavy_check_mark: | :x: | |
> | rozptyl | :heavy_check_mark: | :x: | :x: |
> | smerodajná odchýlka | :heavy_check_mark: | :x: | :x: |
> | Giniho koeficient| | :heavy_check_mark: | :heavy_check_mark: |
> | entropia | | :heavy_check_mark: | :heavy_check_mark: |
### Charakteristiky polohy
> Typická hodnota, která vystihuje danou sadu hodnot. Některé mohou být vhodnější (víc vystihující) než jiné.
> [color=#0047AB]
#### Aritmetický průměr (_mean_) $\bar{x}$
> Součet hodnot dělený počtem hodnot.
> [color=#0047AB]
:::success
$\bar{x} = \frac{1}{n} \sum^{n}_{i=1}{x_i}$
:::
- Lehce ovlivnitelné extrémními hodnotami, možné řešení: `*[MV013]`
- _trimmed mean_ = priemer po odstránení určitého počtu extrémnych hodnôt (používa sa napr. pri športoch, ktoré sú hodnotené porotou -- najnižšie a najvyššie skóre sa zruší, výsledok je priemer zostávajúcich hodnôt),
> **Príklad:** hodnoty 7, 11, 2, 6, 14 $\rightarrow$ usporiadané 2, 6, 7, 11, 14
> $0.2$-trimmed mean = by znamenalo odstranit 20 % nejnižších a 20 % nejvyšších hodnot, tudíž by výsledá sada byla 6, 7, 11.
> [color=purple]
- _winsorized mean_ = priemer po nahradení určitého počtu extrémnych hodnôt menej extrémnymi (najbližšou hodnotou zo sady).
> **Príklad:** Máme sadu 1, 5, 7, 8, 9, 10, 34. Po aplikaci winsorized mean dostaneme 5, 5, 7, 8, 9, 10, 10.
> [color=purple]
#### Medián (_median_) $\widetilde{x}$
> Hodnota nacházející se přesně v polovině **seřazeného** seznamu hodnot.
> Jinak řečeno, polovina hodnot je menší než medián a polovina je větší než medián.
> [color=#0047AB]
:::success
$\widetilde{x} = x_{(\frac{n+1}{2})}$ pre nepárne (liché) $n$, $\widetilde{x} = \frac{x_{(\frac{n}{2})} + x_{(\frac{n}{2}+1)}}{2}$ pre párne (sudé) $n$.
:::
- Ak je počet hodnôt párny (sudý), neexistuje jedna hodnota, ktorá by bola presne v polovici $\rightarrow$ počíta sa priemer z dvoch hodnôt.
- Vhodnejšia charakteristika polohy ako priemer v prípade _skewed_ dát.
- :bulb: $0.5$-kvantil
#### Modus (_mode_)
> Hodnota, která se v sadě hodnot vyskytuje nejčastěji, nemusí být určená jednoznačně.
> [color=#0047AB]
- :bulb: Vhodná charakteristika i pro kategorické proměnné.
#### Kvantil (_quantile_)
> Hodnota, která je větší nebo rovna jako $\alpha \cdot 100$ % hodnot ze sady.
> [color=#0047AB]
:::success
$q_\alpha = x_{(\lceil n\alpha \rceil)}$
:::
- $q_{0.5}$ = medián
- $q_{0.25}$ = 1. kvartil ($Q_1$)
- $q_{0.75}$ = 3. kvartil ($Q_3$)
- $q_{0.75} - q_{0.25}$ = kvartilová odchýlka ($IQR$ = _interquartile range_)
### Charakteristiky variability
#### Rozptyl (_variance_)
> Průměr ze součtu čtverců (_sum of squares_).
> Říká, jak moc se liší hodnoty od průměru.
> [color=#0047AB]
:::success
$s^2 = \frac{1}{n-1}\sum^{n}_{i=1}{(x_i-\bar{x})^2}$
:::
#### Směrodatná odchylka (_standard deviation_)
> Odmocnina z rozptylu.
> Říká, jak moc se průměrně liší jednotlivé hodnoty od průměrné hodnoty.
> Pokud budeme mít v sadě 2 hodnoty: 2 a 4, jejich průměr je 3. Obě dvě hodnoty se liší od průměru o 1. Tudíž směrodatná odchylka je 1.
> [color=#0047AB]
:::success
$s = \sqrt{\frac{1}{n-1}\sum^{n}_{i=1}{(x_i-\bar{x})^2}}$
:::
### Charakteristiky tvaru `*[MV013]`
#### Koeficient šikmosti (_skewness_) `*[MV013]`

> - **Šikmost $= 0$** značí, že hodnoty náhodné veličiny jsou rovnoměrně rozdělené vlevo a vpravo od střední hodnoty.
> - **Šikmost $> 0$** (right-skewed distribution) značí, že vpravo od průměru se vyskytují odlehlejší hodnoty než vlevo (rozdělení má tzv. right tail) a väčšina hodnôt sa nachádza blízko vľavo od priemeru.
> - Pro **šikmost $<0$** (left-skewed distribution) platí opak.
> - **Symetrické** rozdělení (včetně normálního) mají **šikmost $= 0.$**
> - Pro rozdělení s kladnou šikmostí obvykle platí, že modus je menší než medián a ten je menší než střední hodnota (pro zápornou šikmost naopak).
> [name=Wikipedia][color=#0047AB]
#### Koeficient špičatosti (_kurtosis_) `*[MV013]`

> - **Špičatost $> 0$** značí, že **většina hodnot** náhodné veličiny leží **blízko** její **střední hodnoty** a hlavní vliv na rozptyl mají málo pravděpodobné odlehlé hodnoty. Křivka hustoty je špičatější než při normálním rozdělení.
> - **Špičatost $< 0$** značí, že rozdělení je **rovnoměrnější** a křivka jeho hustoty je víc plochá než pri normálním rozdělení.
> - Normálne rozdelenie má špicatosť $= 0$.
> - Špicatosť rozdelenia nezávisí od lineárnej transformácie náhodnej veličiny, je teda napr. rovnaká pre všetky normálne rozdelenia.
> [name=Wikipedie][color=#0047AB]
### Poriadkové štatistiky (výberové charakteristiky dané poradím)
:::warning
:book: http://kfe.fjfi.cvut.cz/~limpouch/sigdat/statodn/node5.html
:book: http://user.mendelu.cz/drapela/Statisticke_metody/teorie%20text%20II.pdf
:::
:::info
**Pořádková statistika** = vzestupně uspořádané prvky souboru $x_{(1)}, x_{(2)}, \ldots, x_{(n)}$.
:::
> Z takto vytvořené pořádkové statistiky lze konstruovat kvantilové charakteristiky.
> [color=#0047AB]
### Statistiky asociace
:::info
Statistiky asociace jsou faktory nebo koeficienty, které **kvantifikují vztah** mezi dvěma nebo vícero veličinami.
:::
#### Kovariance
> Kovariance je statistickou mírou lineární závislosti dvou veličin.
> [name=Wikipedia]
:::success
Nech $x = (x_1, \ldots, x_n)^T$ a $y = (y_1, \ldots, y_n)^T$.
**Kovariance** $c$ je definována následovně:
$$
c = \frac{1}{n-1}\sum^{n}_{i=1}{(x_i-\bar{x})(y_i-\bar{y})}
$$
:::
> Od každého prvku výběru $x$ odečteme výběrový průměr (výběrový průměr je průměr vybraných prvků) $\bar{x}$, od každého prvku výběru $y$ odečteme výběrový průměr $\bar{y}$, rozdíly mezi sebou podle indexů vynásobíme ($(x_1-\bar{x})\cdot(y_1-\bar{y})$, $(x_2-\bar{x})\cdot(y_2-\bar{y})$ atď.), výsledné součiny sčítáme a vydělíme $n-1$.
> [color=#0047AB]
> Vzorec předpokladá, že výběry $x$ a $y$ mají stejnou velikost $n$.
> Pokud je $cov(X, Y) >0$, obě proměnné se mění stejným směrem (pokud roste jedna, roste i druhá a naopak), jsou si úměrné.
> Pokud je $cov(X, Y) <0$, proměnné jsou nepřímo úměrné.
> Pokud je $cov(X, Y) =0$, proměnné na sobě nezávisí.
> Kovariance nám nic neříká o síle vazby - je vyjádřená v jednotkách X a Y.
> [color=#0047AB]
#### Korelace
> Korelace znamená vzájemný vztah mezi dvěma procesy nebo veličinami. Pokud se jedna z nich mění, mění se korelativně i druhá a naopak. Pokud se mezi dvěma procesy ukáže korelace, je pravděpodobné, že na sobě závisejí, nelze z toho však ještě usoudit, že by jeden z nich musel být příčinou a druhý následkem. To samotná korelace nedovoluje rozhodnout, protože korelace neimplikuje kauzalitu.
> [name=Wikipedia]
> :bulb: Korelace je **normalizovaná** kovariance.
> [color=#0047AB]
:::success
Nech $x = (x_1, \ldots, x_n)^T$ a $y = (y_1, \ldots, y_n)^T$.
**Korelácia** $r$ je definovaná nasledovne:
$$
r = \frac{\sum^{n}_{i=1}{(x_i-\bar{x})(y_i-\bar{y})}}{\sqrt{\sum^{n}_{i=1}{(x_i-\bar{x})^2} \sum^{n}_{i=1}{(y_i-\bar{y})^2}}}
$$
:::
> Korelace se počítá podobně jako kovariance, ale čitatel se dělí odmocninou ze součinu **součtu čtverců** (_sum of squares_) pro $x$ a pro $y$.
> [color=#0047AB]
> Hodnota $r > 0.8$ znamená silný pozitivní lineární vztah, $r < -0.8$ silný negativní lineární vztah a $r = 0$ značí, že mezi veličinami neexistuje lineární vztah.
> [color=green]
> Interpretace korelace v přírodních vědách:
> $|\rho| \in \langle0;0,4)$ - malá nebo žádná korelace.
> $|\rho| \in \langle0,4;0,6)$ - slabá korelace
> $|\rho| \in \langle0,6;0,8)$ - střední korelace
> $|\rho| \in \langle0,8;1)$ - silná korelace
> [color=#0047AB]
> Korelace představuje kovarianci na škále $\langle- 1;1\rangle$.
> [color=#0047AB]
#### Matice korelace
:::info
Korelační matice je tabulka, která zobrazuje korelační koeficienty pro vybrané proměnné. Je to dobrý nástroj pro vizualizaci závislostí proměnných v datasetu.
:::

> Korelace mezi "Hours spent studying" a "Exam score" je silně pozitivní, tudíž to znamená, že pokud jsme strávili učením hodně hodin, dosáhli jsme lepších výsledků.
> Kdežto "Hour spent studying" a "Hours spent sleeping" má negativní korelaci, což znamená, že pokud jsme více hodin studovali, tak jsme méně hodin spali a naopak.
> Příklad žádné korelace může být "IQ score" a "Hour spent sleeping". Kolik hodin spánku si dopřáváme nemá prakticky žádný vliv na naše IQ
> [color=#0047AB]
#### Scatterplot
> Vizualizuje hodnoty dvoch premenných v 2D priestore. Využíva sa na sledovanie vzťahov medzi premennými.
> V prípade, že sa scatterplot používa na zobrazenie korelácie medzi premennými, zvykne sa do grafu priložiť krivka, ktorá reprezentuje tento vzťah.
> [color=#0047AB]

> Obrázek ukazuje korelaci výnosů z prodeje zmrzliny v závislosti na venkovní teplotě. Scatterplot vykazuje pozitivní korelaci, protože výnosy zmrzliny byly vyšší při vyšších (teplejších) teplotách.
> [color=#0047AB]
#### Korelogram
> Vizualizuje correlation matrix. Užitočné pri veľkom počte premenných.
> Prakticky stejné jako correlation matrix.
> [color=#0047AB]
Jedna z variánt korelogramu:
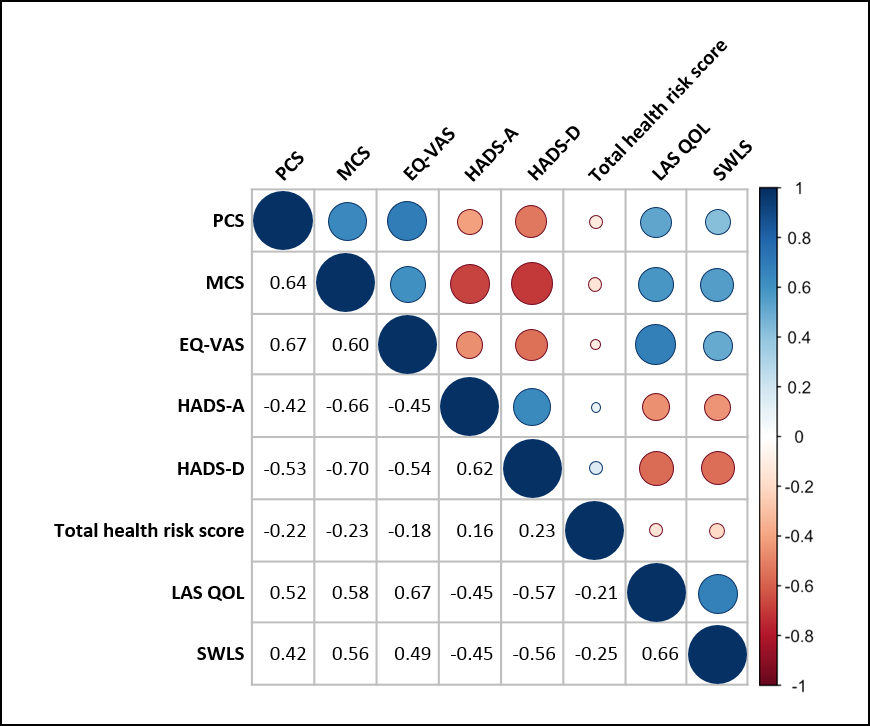
### Používané grafy
#### Boxplot
> Boxplot delí dáta na sekcie obsahujúce približne 25 % dát v dátovom súbore. Poskytujú vizuálnu sumarizáciu, vďaka ktorej je jednoduché rýchle určiť priemer, šikmosť dát, kvantily a extrémne hodnoty (outliers).
> [color=#0047AB]

## Náhodná veličina (_random variable_)
:::info
> **Náhodná veličina** je libovolná veličina, kterou je možné opakovaně měřit a její hodnoty zpracovávat metodami pravděpodobnosti nebo statistiky. Tyto hodnoty jsou před vykonáním experimentu, resp. pozorováním, neznámé.
> [name=Wikipédia][color=lightblue]
>Přesněji, **náhodná veličina** je funkce, která přiřazuje každému elementárnímu náhodnému jevu nějakou (zpravidla číselnou) hodnotu (například při hodu mincí "panně" nulu a "orlu" jedničku).
> [name=Wikipédia][color=lightblue]
:::
:::success
> Nech $(\Omega, \mathcal{A}, P)$ je pravděpodobnostní prostor.
> [name=MV013, 3. prednáška][color=green]
- $\Omega$ = neprázdna množina
- $\mathcal{A}$ = $\sigma$-algebra nad $\Omega$
- $P$ = pravdepodobnostné ohodnotenie nad $\mathcal{A}$
:::
> **Príklady:**
> [color=purple]
> - počet hláv pri 10-krát opakovanom hode mincou,
> - počet dopravných nehôd za deň,
> - doba čakania na autobus,
> - výška náhodne vybraného študenta.
Náhodná veličina môže byť **diskrétna** alebo **spojitá**.
:::warning
:book: [Wikipedie: Náhodná veličina](https://cs.wikipedia.org/wiki/N%C3%A1hodn%C3%A1_veli%C4%8Dina)
:book: https://www.statlect.com/fundamentals-of-probability/random-variables
:::
### Diskrétní náhodná veličina
:::success
Náhodná veličina je **diskrétní**, pokud se prvky výběrového prostoru $\Omega$ zobrazí na ose reálných čísel jako izolované body, označené $x_1, x_2, ..., x_k$, přičem každý z těchto bodů má nenulovou pravděpodobnost.
Pravděpodobnost, že diskrétní náhodná veličina $X$ bude mít po vykonání náhodného pokusu hodnotu $x$, značíme $P(X=x)$ nebo $P(x)$.
Výsledkem jednoho náhodného pokusu bude, že náhodná veličina bude mít právě jednu hodnotu. **Součet pravděpodobností všech možných hodnot $x$ diskrétní náhodné veličiny $X$ je rovný 1**.
$$
\sum_x{P(x)} = 1
$$
:::
:::info
**Diskrétní náhodnou veličinou** je tedy všechno, čo může nabýt jen jednotlivé hodnoty z konečného nebo nekonečného intervalu, tzn. **může se změnit pouze skokově**.
:::
> **Príklad**: pravdepodobnosť hodu kockou -- kocka vie nadobudnúť len hodnoty od 1 po 6.
> [color=purple]
:::success
Rozdelenie pravdepodobnosti diskrétnej náhodnej veličina sa vyjadrí tak, že sa určí pravdepodobnosť $P(x)$ pre všetky $x$ z definičného oboru veličiny $X$. Pravdepodobnosti týchto hodnôt sú vyjadrené funkciou $P(x)$, ktorá sa nazýva **pravdepodobnostnou funkciou**
Platí, že vo výberovom priestore **majú prvky súčet svojich pravdepodobností rovný 1**.
:::
> Hodnoty pravdepodobnostnej funckie sa často vyjadrujú tabuľkou. **Príklad**:
> [color=purple]
>| $x$ | $P(x)$ |
>|-----|------|
>| $x_1$ | 0,2|
>| $x_2$ | 0,3|
>| $x_3$ | 0,5|
> Pravdepodobnostnú funkciu vieme **využiť k výpočtu pravdepodobnosti**. Napríklad pravdepodobnosť, že náhodná veličina $X$ leží medzi hodnotami $x_1$ a $x_2$ môže byť vyjadrená ako $P(x_1 \leq X \leq x_2) = \sum_{x=x_1}^{x_2}{P(x)}$, čo znamená, že **sčítame pravdepodobnosti nadobudnutia hodnôt v danom rozsahu**.
> [color=#0047AB]
>**Rozdelenie početnosti diskrétnej náhodnej veličiny:**
>
:::success
Pomocou pravdepodobnostnej funkcie je možné zaviesť **distribučnú funkciu** vzťahom
$$
F(x) = P(X < x)
$$
Distribuční funkce je **neklesající** a **spojitá zprava**. Hodnoty distribuční funkce leží v rozsahu $0 \leq F(X) \leq 1$. Pro diskrétní náhodnou veličinu $X$ je možné pro libovolné reálné číslo $x$ vyjádřit distribuční funkci vztahem:
$$
F(x) = \sum_{t\leq x}{P(t)}
$$
Distribuční funkce nám říká, s jakou pravděpodobností nabude náhodná veličina hodnoty menší-rovno **x**.
:::
:::success
Pro popis diskrétních náhodných veličin se používají různé charakteristiky. Jednou z nejdůležitějších je **střední hodnota** označená jako $E(X)$, která je definovaná následujícím vzorcem:
$$
E(X) = \sum_{x_k}{x_k}P(X = x_k)
$$
**Rozptyl** náhodné veličiny se značí $D(X)$ a **vyjadřuje velikost odchylek hodnot náhodné veličiny od její střední hodnoty**. Vyjadřuje se jako:
$$
D(X) = \sum_{x_k}{x_k^2}P(X = x_k) - [E(X)]^2
$$
**Směrodatná odchylka**, označená jako $\sigma(X)$, je definovaná jako odmocnina z rozptylu:
$$
\sigma(X) = \sqrt{D(X)}
$$
:::
> Střední hodnota představuje číslo, **okolo kterého kolísají výběrové průměry** vypočítané ze série pozorovaných hodnot náhodné veličiny. Vypočítá se jako součet vynásobení hodnoty náhodné veličiny s její pravděpodobností.
> **Příklad**:
> - Mějme náhodnou veličinu, která s pravděpodobností 0,3 nabývá hodnoty 1, s pravděpodobností 0,2 nabývá hodnoty 2 a s pravděpodobností 0,5 nabývá hodnoty 3.
> Střední hodnota je pak (0,3 × 1) + (0,2 × 2) + (0,5 × 3) = 2,2.
> [color=#0047AB]
### Spojitá náhodná veličina
:::success
Náhodná veličina je **spojitá**, pokud její hodnoty přiřazené prvkům výběrového prostoru $\Omega$ tvoří interval na ose reálných čísel, přičemž každý bod tohoto intervalu má nenulovou pravděpodobnost.
:::
>**Spojitou náhodnou veličinou** je tedy všechno, co nabývá spojité hodnoty. Nabývá hodnoty z konečného nebo nekonečného intervalu, tzn. může se měnit spojitě **bez skoků**.
> [color=#0047AB]
> **Príklad**: doba čakania na šalinu, analógový signál
> [color=purple]
:::info
Hustota pravděpodobnosti popisuje chování náhodné veličiny. Hustota představuje ekvivalent pravděpodobnostní funkce diskrétní náhodné veličiny, a teda platí:
$$
\int_{-\infty}^{\infty} f(x)dx = 1
$$
Pravděpodobnost, že spojitá náhodná veličina nabyde hodnoty z intervalu $\langle x_1;x_2 \rangle$ může být vypočítáná jako:
$$
P(x_1 \leq X \leq x_2) = \int_{x_1}^{x_2} f(t)dt
$$
:::
>Plocha pod křivkou rozdělení se rovná jedné, protože pokrývá všechny hodnoty, které může náhodná veličina nabývat.
> [color=#0047AB]
:::success
**Distribuční funkce** spojitá náhodná veličiny $X$ je nezáporná funkce:
$$
F(x) = \int_{-\infty}^{x} f(t) dt
$$
Distribuční funkci $F(x)$ je možné vyjádřit jako **plochu pod křivkou pravděpodobnostního rozdělení**.
Pravděpodobnost, že spojitá náhodná veličina nabyde hodnoty z intervalu $\langle x_1;x_2 \rangle$ může být zároveň vyjádřená i pomocí distribuční funkce, a to následujícím způsobem:
$$
P(x_1 \leq X \leq x_2) = F(x_2) - F(x_1)
$$
:::
>Od pravdepodobnosti, že náhodná veličina $X$ nadobudne hodnoty $x_2$ a menšie odčítame pravdepodobnosť, že nadobude hodnoty $x_1$ a menšie. Ostane nám teda plocha medzi bodmi $x_2$ a $x_1$, ktorá značí pravdepodobnosť, že $X$ nadobudne hodnoty v tomto intervale.
> [color=#0047AB]
>**Vyznačení hodnoty distribuční funkce $F(x_i)$:**
>
:::success
K popisu spojité náhodné veličiny se používají číselné charakteristiky. Nejdůležitější z nich je **střední hodnota** (očekávaná hodnota), označovaná jako $E(X)$, ekvivalentně i $EX$, definovaná jako:
$$
E(X) = \int_{-\infty}^{\infty} xf(x)dx
$$
Další charakteristikou je **rozptyl**, označovaný jako $D(X)$ nebo i $var(X)$, který je možné vyjádřit jako:
$$
D(X) = \int_{-\infty}^{\infty} x^2f(x)dx - [E(X)]^2
$$
K popisu hodnot rozptýlení spojité náhodné veličiny se používá nejčastěji **směrodatná odchylka**, označená jako $\sigma(X)$. Je definovaná jako:
$$
\sigma(X) = \sqrt{D(X)}
$$
:::
> Střední hodnota u spojité náhodné veličiny má stejný význam jako při diskrétní.
> Příklad
> - Mějme náhodnou veličinu, jejíž hustota pravděpodobnosti na intervalu <0,1> je f(x) = 2x, jinde identicky rovna nule. To je rozdělení, v němž je hustota pravděpodobnosti přímo úměrná hodnotě x.
> - Střední hodnota uvedené náhodné veličiny tedy je $\frac{2}{3}$.
> [color=#0047AB]
## Náhodný výběr
:::success
**Náhodný výber** je uspořádaná n-tice náhodných veličin $X_1, \ldots, X_n$, které jsou stochasticky **nezávislé** a mají **stejné rozdělení** (ale nemusíme ho konkrétně znát).
Realizací náhodného výběru jsou konkrétní hodnoty $x_1, \ldots, x_n$.
:::
> Příklad: Budeme chtít získat informace o průměrném platu v ČR. Abychom měli přesné informace, museli bychom se zeptat všech občanů na jejich plat. Toto je prakticky neproveditelné, proto učiníme náhodný výběr lidí a těch se zeptáme na jejich plat, z čehož vypočítáme průměr.
> [color=#0047AB]
:::info
**Statistika** je libovolná funkce náhodného výběru.
:::
:::warning
:book: https://mathstat.econ.muni.cz/media/12421/nahodny_vyber_statistika.pdf
:book: https://web.vscht.cz/~zikmundm/astat/poznamky_k_AS_7.pdf
:::
## Parametrické pravděpodobnostní modely NV (distribuce)
:::warning
:bar_chart: Pre fajnšmekrov: [Databáza rozdelení pravdepodobnosti](https://sites.google.com/site/probonto/)
:book: Pre menších fajnšmekrov: [Tabuľka vzťahov medzi rozdeleniami](https://www.statlect.com/probability-distributions/)
:::
### Diskrétní rozdělení
#### Bernoulliho (Binomické) rozdělení (alternativní)
:::info
Popisuje události s **dvěma možnými výsledky** (úspěch, neúspěch), přičemž úspěch má pravděpodobnost $p$, neúspěch $1-p$.
:::
> :bulb: $\text{Bernoulli}(p)$ = $\text{Binomial}(1, p)$
> [color=#0047AB]
> **Príklad:** Hod mincí.
> [color=purple]
:::success
Náhodná veličina $X$ má **Bernoulliho rozdělení** s parametrem $p \in (0, 1)$ pokud je její pravděpodobnostní funkce definována následovně:
$$
p(x) = P(X = x) =
\begin{cases}
1 - p & x = 0 \\
p & x = 1 \\
0 & \text{jinak.}
\end{cases}
$$
- $X \sim \text{Bernoulli}(p)$
- $EX = p$
- $\text{var}X = p(1-p)$
:::
> **Pravděpodobnostní funkce** pro $p=0.65$
>
> 
>
> **Distribuční funkce** pro $p=0.65$
>
> 
#### Binomické rozdělení
:::info
Popisuje **počet úspěchů** v $n$ opakovaných (mezi sebou nezávislých) Bernoulliho pokusech, přičemž $p$ je pravděpodobnost úspěchu v jednom pokusu.
:::
> **Příklad:** Hazíme desetkrát kostkou, jaká je pravděpodobnost, že právě čtyřikrát padne šestka?
> [color=purple]
:::success
Náhodná veličina $X$ má **binomické rozdělení** s parametry $n \in \mathbb{N}$ a $p \in (0,1)$ pokud je její pravděpodobnostní funkce definovaná následovně:
$$
p(x) = P(X = x) =
\begin{cases}
{n \choose x} p^x(1-p)^{n-x} & x = 0, 1, \ldots, n \\
0 & \text{jinak.}
\end{cases}
$$
- $X \sim \text{Binomial}(n,p)$
- $EX = np$
_(čím vyšší pravděpodobnost úspěchu, tím větší počet úspěšných pokusů)_
- $\text{var}X = np(1-p)$
:::
> **Pravděpodobnostní funkce:**
>
> 
>
> _Pozn.: graf pripomína pravdepodobnostnú funkciu normálneho rozdelenia, viď napr. aproximácia normálnym rozdelením pomocou centrálnej limitnej vety._
>
> **Distribuční funkce:**
>
> 
#### Poissonovo rozdělení
:::info
Popisuje **počet výskytův nezávislé události za fixní** (časový/prostorový/...) **interval**.
:::
> **Príklad:** počet příchozích hovorů do call centra za hodinu; počet narozených dětí v Česku za den
> [Příklad na poissonovo rozdělení](https://is.muni.cz/do/rect/el/estud/prif/ps15/statistika/web/pages/poissonovo-rozd.html).
> [color=purple]
:::success
Náhodná veličina $X$ má **Poissonovo rozdělení** s parametrem $\lambda > 0$ pokud je její pravděpodobnostní funkce definovaná následovně:
$$
p(x) = P(X = x) =
\begin{cases}
e^{-\lambda\frac{\lambda^x}{x!}} & x = 0, 1, ..., \\
0 & \text{inak.}
\end{cases}
$$
- $X \sim \text{Pois}(\lambda)$
- $EX = \lambda$
- $\text{var}X = \lambda$
- $\lambda$ = očekávaný počet výskytů události za daný interval
:::
> **Pravdepodobnostná funkcia:**
>
> 
>
> **Distribučná funkcia:**
>
> 
#### Geometrické rozdělení
:::info
Popisuje **počet selhání** v opakovaném Bernoulliho experimentu **před prvním úspěchem**.
:::
> **Příklad:** počet selhání než na kostce hodíme šestku; počet přenesených bitů než se stane první chyba (pokud přenášíme pouze do první chyby).
> [color=purple]
:::success
Náhodná veličina $X$ má **geometrické rozdělení** s parametrem $p \in (0, 1)$ pokud je její pravděpodobnostní funkce definovaná následovně:
$$
p(x) = P(X = x) =
\begin{cases}
p(1-p)^x & x = 0, 1, \ldots, \\
0 & \text{inak.}
\end{cases}
$$
- $X \sim \text{Geom}(p)$
- $EX = \frac{1-p}{p}$
- $\text{var}X = \frac{1-p}{p^2}$
:::
> Někdy se definuje i jako $p(x) = p(1-p)^{x-1}$ pro $x = 1, 2, \ldots$, podle toho, jestli nás zajímá počet selhání před úspěchem (vyšší) nebo počet pokusů potřebných na dosáhnutí prvního úspěchu (tj. pokus včetně toho úspěšného).
> [color=green]
> **Pravděpodobnostní funkce:**
> (vľavo definícia "vrátane", vpravo definícia "počet zlyhaní")
> 
>
> **Distribučná funkcia:**
> (vľavo definícia "vrátane", vpravo definícia "počet zlyhaní")
> 
#### (Diskrétní) rovnoměrné rozdělení
:::info
Stejná pravděpodobnost pro každý jev z množiny $A$.
:::
> **Příklad**: poslední cifra náhodně vybraného telefonního čísla; házení kostkou
> [color=purple]
:::success
Náhodná veličina $X$ má **diskrétní rovnoměrné rozdělení** na konečné množině $A$ pokud je její pravděpodobnostní funkce definovaná následovně:
$$
p(x) = P(X = x) =
\begin{cases}
\frac{1}{A} & x \in A, \\
0 & \text{jinak.}
\end{cases}
$$
- $X \sim \text{Uniform}(A)$
- neexistuje všeobecný vzorec pro $EX$ a ani $\text{var}X$
:::
> **Pravděpodobnostní funkce:**
>
> 
>
> **Distribuční funkce:**
>
> 
### Spojité rozdělení
#### Rovnoměrné rozdělení
:::info
Přiřazuje všem hodnotám náhodné veličiny **stejnou pravděpodobnost**. Používá se při generování pseudonáhodných čísel.
:::
:::success
Spojitá náhodná veličina X má **rovnoměrné rozdělení** na intervalu $(a,b)$, kde parametry $a,b$ jsou libovolné reálné čísla, pro které platí, že $a<b$ právě tehdy, pokud její hustota pravděpodobnosti má následující tvar:
$$
f(x) =
\begin{cases}
\frac{1}{b-a}; x \in (a,b), \\
0 ; x \notin (a,b)
\end{cases}
$$
Distribuční funkce má tvar:
$$
F(x) =
\begin{cases}
0; x < 0, \\
\frac{x-a}{b-a}; a < x < b, \\
1; x \geq b
\end{cases}
$$
- $X \sim \text{R}(a,b)$
- $E(X) = \frac{a+b}{2}$
- $\text{var}(X) = \frac{(b-a)^2}{12}$
:::
>**Funkce hustoty rozdělení**:
>
>
> [color=purple]
#### Exponenciální rozdělení
:::info
Vyjadřuje **čas mezi náhodně se vyskytujícími událostmi**. Využíva se například v pojistné matematice pri určení času mezi pojistnými událostmi. Pravděpodobnost nástání události nezávisí na přečkané době.
:::
:::success
Spojitá náhodná veličina X má **exponenciální rozdělení** s parametrem $\lambda > 0$ právě tehdy, pokud její hustota pravděpodobnosti má následující tvar:
$$
f_x(x) =
\begin{cases}
\lambda e^{-\lambda x}; x > 0, \\
0 ; x \leq 0
\end{cases}
$$
Distribučná funkcia má tvar:
$$
F(x) =
\begin{cases}
1 - e^{-\lambda x}; x > 0, \\
0 ; x \leq 0
\end{cases}
$$
- $X \sim \text{Exp}(\lambda)$
- $E(X) = \frac{1}{\lambda}$
- $\text{var}(X) = \frac{1}{\lambda^2}$
:::
> Příklad: (https://is.muni.cz/do/rect/el/estud/prif/ps15/statistika/web/pages/exponencialni.html)
>**Hustota exponenciálneho rozdelenia:**
>
> [color=#0047AB]
> [color=purple]
#### Normálne rozdelenie
:::info
Normálne rozdělení, někdy nazývané i **Gaussovo rozdělení**, je najčastejšie používané rozdelenie. Má mnoho významných teoretických vlastností a z hľadiska aplikácie býva vhodné na vyjadrenie náhodných veličín, ktoré je možné interpretovať ako aditívny výsledok veľa nezávislých vplyvov (chyba merania, odchýlka rozmeru výrobku od požadovanej hodnoty, atď).
:::
:::success
**Normálne rozdelenie** pravdepodobnosti s parametrami $\mu$ (střední hodnota) a $\sigma^2$ (směrodatná odchylka), kde $\sigma%2 > 0$ má hustotu:
$$
f(x) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
$$
- $X \sim \text{N}(\mu, \sigma^2)$
- $E(X) = \mu$
- $\text{var}(X) = \sigma^2$
\
Rozdelenie $\text{N}(0, 1)$ sa označuje ako **normované alebo štandardizované normálne rozdelenie**. Toto rozdelenie má teda hustotu:
$$
f(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}
$$
:::
>**Grafy hustôt normálneho rozdelenia:**
>
>
>
>**Grafy odpovedajúcich distribučných funkcií:**
>
>
:::success
**Transformáciou** náhodnej veličiny $X$ s rozdelením $N(\mu, \sigma^2)$ na náhodnú veličinu
$$
U = \frac{X - \mu}{\sigma}
$$
dostaneme náhodnú veličinu s **normovaným (standardizovaným) normálním rozdělením** $\text{N}(0, 1)$ a distribučnou funkciou $F(u)$.
:::
> Zmenšování parametru $\mu$ posouvá rozdělení po ose $x$ vlevo, zvětšování ho posouvá vpravo. Čím větší je parameter $\sigma^2$, tým víc plochá je křivka (hodnoty se víc liší od průměru). Standardizací se od náhodné veličiny odečítá její střední hodnota $\mu$, čímž se křivka posune na x-ové ose na bod 0.
> [color=#0047AB]
:::success
Pre hodnoty $F(u)$ distribučnej funkcie normovaného normálneho rozdelenia platí
$$
F(-u) = 1 - F(u)
$$
dostaneme náhodnou veličinu s **normovaným (standardizovaným) normálním rozdělením** $\text{N}(0, 1)$.
Pre kvantily normovaného normálneho rozdelenia platí
$$
u_{1-P} = -u_P
$$
kde $0 < P < 1$.
:::
> Tieto vlastnosti plynú zo stredovej symetrie rozloženia. Pre ilustráciu si môžeme za $u$ pri výpočte hodnoty distribučnej funkcie dosadiť číslo 0,5. Po odčítaní hodnoty $F(0,5)$ od 1 dostaneme pravdepodobnosť, ktorá je vďaka stredovej symetrii rovnaká ako $F(-0,5)$
> [color=#0047AB]
>
:::success
Ak má náhodná veličina $X$ normálne rozloženie $N(\mu, \sigma^2)$, jej distribučnú funkciu je možné vyjadriť ako
$$
F(X) = F(\frac{x-\mu}{\sigma})
$$
:::
> [color=#0047AB]
> [color=purple]
#### Chi-kvadrát rozdělení
:::info
Rozdělení se používá při určování intervalových odhadů neznámých parametrů a při testování hypotéz, například když chceme určit, zda množina dat vyhovuje dané distribuční funkci - viz. https://www.youtube.com/watch?v=2QeDRsxSF9M.
:::
:::success
Rozdelenie **chi kvadrát**, taktiež nazývané aj **Pearsonovo rozdelenie**, s $n$ stupňami voľnosti je spojité rozdelenie pravdepodobnosti. Hustota pravdepodobnosti rozdelenia má tvar
$$
f(x) =
\begin{cases}
0; x \leq 0, \\
\frac{1}{\Gamma(\frac{n}{2})2^{\frac{n}{2}}}e^{-\frac{x}{2}}x^{\frac{n}{2}-1} ; x > 0
\end{cases}
$$
- $X \sim \chi^2(n)$
- $E(X) = n$
- $\text{var}(X) = 2n$
:::
>**Grafy hustôt chi kvadrát rozdelenia:**
>$k$ značí počet stupňov voľnosti
>
> [color=#0047AB]
> [color=purple]
#### Logaritmicko-normálne rozdelenie
:::info
Logaritmicko-normálne rozdelenie s parametrami $\mu$ a $\sigma$ je spojité rozdělení pravděpodobnosti jednorozmernej reálnej náhodnej veličiny $X$ také, že náhodná veličina $ln(X)$ má normálne rozdelenie so strednou hodnotou $\mu$ a smerodajnou odchýlkou $\sigma$.
:::
:::success
Hustota **logaritmicko-normálneho rozdelenia** má tvar
$$
fx(x) = \frac{1}{x\sigma\sqrt{2\pi}} e^{-\frac{(ln x-\mu)^2}{2\sigma^2}}, x > 0
$$
- $X \sim LN(\mu, \sigma)$
- $EX = e^{\mu + \sigma^2/2}$
- $\text{var}X = (e^{\sigma^2} - 1)e^{2\mu + \sigma^2}$
:::
>**Hustoty logaritmicko-normálneho rozdelnia:**
>
> [color=#0047AB]
> [color=purple]
#### Studentovo t-rozdelenie
:::info
Studentovo rozloženie je spojité rozdelenie pravdepodobnosti, ktoré sa najčastejšie používa pri **určovaní intervalových odhadov a pri testovaní štatistických hypotéz**.
:::
:::success
Nech $X$ je náhodná veličina a $n$ je prirodzené číslo. Potom táto náhodná veličina $X$ má **Studentovo rozloženie** (taktiež nazývané aj **t-rozloženie**) s $n$ stupňami voľnosti, pokiaľ jej hustota pravdepodobnosti má nasledovný tvar
$$
f_n(x) = \frac{\Gamma(\frac{n+1}{2})}{\Gamma \frac{n}{2} \sqrt{n\pi}} (1+\frac{x^2}{n})^{-\frac{n+1}{2}}
$$
- $X \sim \text{t}(n)$
- $EX = \mu$
- $\text{var}X = \sigma^2$
:::
> Stupne voľnosti reprezentujú počet nezávislých údajov, na ktorých je založený parametrický odhad.
> [color=#0047AB]
> **Funkcia hustoty Studentovho rozdelenia:**
> ($v$ značí počet stupňov voľnosti)
> 
> [color=#0047AB]
> [color=purple]
## Centrální limitní věta (CLV, _Central Limit Theorem_)
:::warning
:book: [CLV na portálu matematické biologie](https://portal.matematickabiologie.cz/index.php?pg=aplikovana-analyza-klinickych-a-biologickych-dat--biostatistika-pro-matematickou-biologii--bodove-a-intervalove-odhady--teoreticke-pozadi-intervalovych-odhadu--centralni-limitni-veta)
:movie_camera: [StatQuest: The Central Limit Theorem [YouTube] - Perfektně vysvětleno](https://www.youtube.com/watch?v=YAlJCEDH2uY)
:::
> **Centrální limitní věta** je klíčové matematické tvrzení, které popisuje pravděpodobnostní chování **výběrového průměru pro velké vzorky** a umožňuje tak sestrojení intervalových odhadů, a to nejen pro normálně rozdělené náhodné veličiny.
> [color=#0047AB]
:::success
**_Lindeberg-Lévy CLV_**
Mějme posloupnost $X_1, \ldots, X_n$ nezávislých, stejně rozdělených náhodných veličin (a.k.a. **náhodný výběr**), které mají konečnou střední hodnotu $\mu$ a rozptyl $\sigma^2 > 0$. Pak asymptoticky pro $n \rightarrow \infty$ platí:
$$
(1)\quad\overline{X} = \frac{1}{n}\sum^{n}_{i=1}{X_i} \approx \mathcal{N}(\mu, \frac{\sigma^2}{n}) \\
(2)\quad\sqrt{n}\frac{\overline{X}-\mu}{\sqrt{\sigma^2}} \approx \mathcal{N}(0,1) \\
(3)\quad\frac{\sum^{n}_{i=1}{X_i - n\mu}}{\sqrt{n\sigma^2}} \approx \mathcal{N}(0,1)
$$
:::
> Komentář: bez ohledu na to, z jakého rozdělení máme náhodné výběry, výběrový průměr bude mít (pro dostatečně velké $n$) asymptoticky normální rozdělení s určitými parametry (viz. $(1)$ výše). Po vhodné normalizaci výběrového průměru dostaneme asymptoticky standardní normální rozdělení $\mathcal{N}(0,1)$ (viz. $(2)$ a $(3)$ výše).
> Díky CLV nepotřebujeme vědět, z jakého rozložení pocházejí naše hodnoty. Pokud máme hodnoty výběrového průměru (které dle CLV budou mít normální rozložení), můžeme z nich počítat confidence intervaly, dělat t-testy (kde se ptáme, jestli jsou nějaké rozdíly mezi výběrovými průměry dvou vzorků), ANOVA a další statistické analýzy, které počítají s výběrovým průměrem.
> [color=#0047AB]
> :bulb: Centrální limitní věta funguje dokonce i tehdy, když rozdělení původní náhodné veličiny není spojité, ale **diskrétní**.
> [color=#0047AB]
:::info
**Zjednodušená interpretace CLV**: pokud je rozdělení pravděpodobnosti náhodné veličiny $X$ **normální**, pak je i **rozdělení průměru** pozorovaných hodnot **normální** (a to i pro $n = 1$). Pokud však rozdělení pravděpodobnosti náhodné veličiny $X$ normální není, pak je rozdělení průměru pozorovaných hodnot **přibližně normální**, když **$n$ je dostatečně velké** (matematicky řečeno, pro $n$ jdoucí do nekonečna).
:::
> **Minimální velikost souboru** pro výpočet průměru (Lindeberg-Lévy):
> [color=#0047AB]
> - $n \ge 30$ v případě rozdělení pravděpodobnosti podobných normálnímu;
> - $n \ge 100$ pro rozdělení, která nejsou podobná normálnímu
>
> *(názory na minimální hodnoty $n$ se liší)*
> Teorie a zároveň **princip použití CLV** pro výpočet pravděpodobnosti:
> 
> [name=MV013, lecture 4][color=green]
> cdf = cumulative distribution function (distribuční funkce)
> 
> 
> [name=MV013, lecture 4][color=green]
> **Příklad** výpočtu s použitím CLV
> 
> [name=MV013, lecture 4][color=purple]
> :::info
> :bulb: _Continuity correction_ (oprava na spojitost) se používá při aproximaci diskrétního rozdělení spojitým.
> V případě uvedeném výše, kde jsme v prvním případě (spojité) spočítali, že pravděpodobnost, že ze 100 hodů padne nanejvýš 15 šestek (P(X < 16)), je 0.429 (vzali jsme distribuční funkci a spočítali F(16)). V druhém případě jsme se dívali na diskrétní pravděpodobnost P(X $\le$ 15), tzn. F(15) = 0.327, což je jiný výsledek než 0.429. Pro tento případ využijeme _continuity correction_ a spočítáme F(15.5) = 0.377.
>
> Pro diskrétní rozdělení $P(X \le x) = P(X \lt x + 1)$. Pokud platí podmínky Moivre-Laplaceové CLV, dá se výše uvedené aproximovat pomocí $P(Y \lt x + 0.5)$
> :::
## Bodové a intervalové odhady, princip věrohodnosti
> Cílem odhadu je určení neznámého parametru náhodné veličiny $X$ na základě informace obsažené ve výběrovém souboru (realizace náhodné veličiny, datasetu). Zajímá nás především **hodnota a přesnost odhadu**.
> Většinou chceme odhadnout průměr nebo rozptyl (variance).
> Například chceme odhadnout průměrný plat v ČR. Abychom měli přesnou hodnotu, museli bychom znát plat každého člověka v ČR, což je nemožné. Učiníme proto náhodný výběr vzorku populace, zjistíme jejich platy a na základě toho vypočítáme (odhaneme) průměrný plat v celé ČR.
> [color=#0047AB]
:::info
**Nestranný odhad _(unbiased estimator)_** parametru $\theta$ je odhad, jehož střední hodnota je rovna θ a to pro každou hodnotu, které může tento parametr ze své definice nabývat. Nestrannost odhadu je celkem logickým omezením, které nám říká, že tento odhad má vzhledem ke střední hodnotě nulové vychýlení.
Odhad je **unbiased**, pokud se průměrně rovná pravé hodnotě odhadovaného parametru.
https://stats.stackexchange.com/a/31047
**Nejlepší nestranný odhad** má ze všech nestranných odhadů nejmenší rozptyl (variabilitu).
:::
> **Příklad nestranného odhadu:** výběrový průměr jako odhad střední hodnoty (parametru $\mu$) normálního rozdělení.
> [color=purple]
:::info
**Konzistentní odhad _(consistent estimator)_** odhad je konzistentní, pokud se zvětšujícím se vzorkem konverguje k pravé hodnotě odhadovaného parametru. _To be slightly more precise - consistency means that, as the sample size increases, the sampling distribution of the estimator becomes increasingly concentrated at the true parameter value._
https://stats.stackexchange.com/a/31047
:::
### Bodový odhad (_point estimate_)
> Parametr odhadujeme pomocí **jedné hodnoty**, která se snaží hodnotu parametru **aproximovat**.
> [color=#0047AB]
> 
> [color=green]
> 
> [name=MV011]
> Příklad použití je stejný, jako uvedený výše s odhadováním platu.
### Intervalový odhad (_range estimate_)
> Parametr odhadujeme pomocí **intervalu**, který daný parametr s velkou pravděpodobností obsahuje. Délka intervalu vypovídá o přesnosti odhadu.
>
> Příklad: Chceme odhadnout průměrnou výšku lidí v České republice. Proto učíníme několik náhodných výběrů lidí (např. 10x vybere náhodně 10 lidí). Z techto vybraných skupin pro každou vypočítáme výběrový průměr (sample mean). Tyto výběrové průměry nám dávají "confidence interval", který říká, že průměr celé populace s velkou pravděpodobností spadá do confidence intervalu. Viz. https://youtu.be/ENnlSlvQHO0
> [color=#0047AB]
:::success
**Interval spolehlivosti** (**konfidenční interval**) pro parametr $\theta$ se spolehlivostí $1 - \alpha$, kde $\alpha \in [0,1]$, je dvojice statistik $(T_d(\mathbf{X}), T_h(\mathbf{X}))$ taková, že
$$P(T_d(\mathbf{X}) \leq \theta \leq T_h(\mathbf{X})) = 1 - \alpha$$
:::
> * **Intervalový odhad** je konkrétní realizace intervalu spolehlivosti.
> * Koeficient $\alpha$ nazýváme **hladinou významnosti**.
> * Pro **oboustranný** intervalový odhad platí $P(\theta \leq T_d(\mathbf{X})) = P(\theta \geq T_h(\mathbf{X})) = \frac{\alpha}{2}$
> * Pro **levostranný** (dolní) intervalový odhad platí $P(T_d(\mathbf{X}) \leq \theta) = 1 - \alpha$
> * Pro **pravostranný** (horní) intervalový odhad platí $P(\theta \leq T_h(\mathbf{X})) = 1 - \alpha$
> [color=green]
> 
> #### Tvorba intervalového odhadu
> 1. Zvolíme vhodnou výběrovou charakteristiku $T(\mathbf{X})$ jejíž rozdělení závislé na $\theta$ známe.
> 2. Určíme $\alpha$ a kvantily $t_{\frac{\alpha}{2}}$ a $t_{1-\frac{\alpha}{2}}$ z $T(\mathbf{X})$
> 3. Stanovíme meze pro $\theta$ z podmínky $t_{\frac{\alpha}{2}} \leq T(\mathbf{X}) \leq t_{1 - \frac{\alpha}{2}}$
> 4. Profit!
> [color=#0047AB]
> **Příklad:** intervalový odhad střední hodnoty $\mu$ **normálního rozdělení** s neznámým rozptylem se spolehlivostí $0.95$. Máme vzorek velikosti $n$ s výběrovým průměrem $\bar{X}$ a výběrovým rozptylem $S^2$.
> 1. Zvolíme statistiku $T(\mathbf{X}) = \frac{\overline{X} - \mu}{S}\sqrt{n}$
> 2. Z vlastností Studentova rozdělení víme: $T(\mathbf{X}) \sim t(n-1)$
> 3. Dosadíme:
> $$P(t_{\frac{\alpha}{2}}(n-1) \leq \frac{\bar{X} - \mu}{S} \sqrt{n} \leq t_{1 - \frac{\alpha}{2}}(n-1)) = 0.95$$
> 4. Využijeme $t_{\frac{\alpha}{2}}(n-1) = -t_{1-\frac{\alpha}{2}}(n-1)$, tedy:
> $$P(-t_{1-\frac{\alpha}{2}}(n-1) \leq \frac{\bar{X} - \mu}{S} \sqrt{n} \leq t_{1 - \frac{\alpha}{2}}(n-1)) = 0.95$$
> 5. Vytáhneme vše z prostředku:
> $$P(\bar{X}-\frac{S}{\sqrt{n}}t_{1-\frac{\alpha}{2}}(n-1) \leq \mu \leq \bar{X}+\frac{S}{\sqrt{n}}t_{1-\frac{\alpha}{2}}(n-1)) = 0.95$$
> 6. Vyčíslíme.
> [color=purple]
### Princip věrohodnosti (_likelihood principle_)
#### Maximum likelihood estimate
:::warning
:movie_camera: [StatQuest MLE - dobře vysvětleno - stačí prvních 8 minut](https://www.youtube.com/watch?v=Dn6b9fCIUpM)
:::
:::info
MLE se snaží na základě jednotlivých data pointů odhadnout distribuci datasetu.
:::
> Log-likelihood funkce a likelihood funkce mají maximum ve stejném bodě, s log-likelihoodom se lépe pracuje.
> [color=#0047AB]
Alternatívní metody odhadování parametrů:
- _method of moments_
- _ordinary least-squares method_
Obě metody jsou neparametrické -> MLE využívá informáci o rozdělení pravděpodobnosti a je _most efficient estimator_.
Nevýhody: složitější výpočet, potřeba řešit předpoklady o rozdělení (v případě potřeby se dá použít CLV).
## Statistická inference -- testování hypotéz
:::warning
:book: [Príklady voľby štatistík pri rôznych testoch](https://k101.unob.cz/~neubauer/pdf/testy_hypotez2.pdf)
:::
> Cílem testování hypotéz je oveřit, jestli data **nepopírají předpoklad** (hypotézu).
> [color=#0047AB]
Nulová hypotéza $H_0$
Alternativní hypotéza $H_1$
> Alternatívní hypotéza je to, co nás ve skutečnosti zajímá.
> [color=#0047AB]
> $p$-value je pravděpodobnost, že při platnosti $H_0$ nabývá testová statistika $T$ své stávající hodnoty anebo hodnot ještě extrémnějších
> Zároveň je to taky nejmenší hladina významnosti, při které ještě zamítáme $H_0$
> Pokud je $p$-value menší než $\alpha$, **zamítáme** $H_0$
> Pokud je $p$-value větší než $\alpha$, **nezamítáme** $H_0$
> :movie_camera: [StatQuest - p-value explained](https://www.youtube.com/watch?v=5Z9OIYA8He8)
> [color=#0047AB]
#### Chyby v testovaní hypotéz
:::info
Chyba 1. typu nastane, když **odmítneme** $H_0$ navzdory tomu, že ve skutečnosti **platí**.
Chyba 2. typu nastane, když **neodmítneme** $H_0$ navzdory tomu, že ve skutečnosti **neplatí**.
:::
| | $H_0$ platí | $H_1$ platí |
| ------------------ | --------------------- | --------------------- |
| odmítáme $H_0$ | :x: chyba 1. typu | :heavy_check_mark: OK |
| neodmítáme $H_0$ | :heavy_check_mark: OK | :x: chyba 2. typu |
> 
[color=green]
### Parametrické testy
#### ANOVA
> **ANOVA** (**AN**alysis **O**f **VA**riance) je **parametrickým** testem testujícím zda na hodnotu náhodné veličiny má statisticky významný vliv hodnota některého znaku, který se u náhodné veličiny dá pozorovat.
> [color=#0047AB]
### Neparametrické testy
> Motivací pro neparametrické testy je fakt, že pro parametrické testy je třeba splnit podmínky (normalita, homogenita, …). Nevýhodou neparametrických je však slabší test (tedy zamítnutí $H_0$ je méně pravděpodobné).
> [color=#0047AB]
## Lineární regresní model
:::info
Linear regression model je matematická metoda používaná pro proložení souboru bodů v grafu přímkou.
:movie_camera: [StatQuest - Linear Regression](https://www.youtube.com/watch?v=nk2CQITm_eo)
:::
Příklad lineární regrese

### Least squares estimate (metoda nejmenších čtverců)
:::info
Lineární regrese představuje aproximaci daných hodnot přímkou metodou nejmenších čtverců. Zkusíme body proložit přímkou a od každého z nich vypočítat vzdálenost k přímce (tato vzdálenost se nazýva "**residual**"). Toto opakujeme tak dlouho, dokud suma "residuals" není nejmenší.

:::
### Is this a linear regression model?
> 
> Ano, toto je linear regression model.
> Je to model $Y_i = \beta_0 +\beta_1\ \log x_i + e_i$
> Lineárni model znamená, že je lineární v parametrech $\beta_j$, ne nutně v regressorech $x_i$.
> [name=MV013-11.pdf slide 23]
### Outliers and leverage observations
> Outlier point (odlehlý) je bod, který se značně liší od ostatních bodů a zároveň nesedí do našeho modelu.
> - Například. člověk co měří 3 metry a váží 50 kilo bude outlier.
> Leverage point (pákový) je bod, který se také značně liší od ostatních hodnot, ale má velký vliv na odhad našich parametrů.
> 
> Skupina 1 - jsou to outliers, ale ne leverage points
> Skupina 2 - Leverage points, ale nejsou to outliers
> Skupina 3 - Leverage points a zároveň outliers.
#### Model with outlier and without outlier
> 
> Na grafu je znázorněn model s outlier bodem (outlier bod je označen modrou barvou a model tlustou čárou). Model s tentou čárou nebere tento bod v potaz a je vyznačen tenkou čárou.
:::info
**Linear regression - final remarks**
Nevýhody:
- Velmi silné assumptions
- Prakticky odhadujeme jen na základě dat
- Citlivé na leverage body a outliers
- To je zřejmé, jeden leverage/outlier bod nám změní celý model
- Je nestabilní pro silně korelované regresory.
- ?
- Nedokáže se vypořádat s chybějícími hodnotami.
Výhody:
- Jednoduchá interpretace
- Přímá kvantifikace vlivu jednotlivých regresorů na konečný model.
- Dokážeme vypočítat jak jednotlivý bod ovlivňuje konečný model.
- Many generalizations
- ?
- Dokáže pracovat s numerickými i kategorickými proměnnými.
- It does not suffer from the curse of dimensionality
- ?
:::