# Polynomial Commitment Scheme

## 목적

Verifier는 Prover가 알고 있는 다항식 p를 특정 점에서 평가한 값, p(z)를 알고 싶다.
그런데 다항식 p를 숨기면서 p(z) = 4 라고 알려주면 맞는지 틀린지 알 수가 없다. 따라서 다항식 p를 Prover 마음대로 바꿀 수 없게 고정하는 장치가 필요하고 이것이 Polynomial Commitment Scheme이다.

### Trivial polynomial commitment scheme

Prover가 p의 모든 계수를 Verifier에게 보내주면 Verifier는 p(z)를 직접 계산할 수 있다. 하지만 문제가 있다.

- not succinct: 다항식의 차수와 commitment의 크기는 linear 관계이다.
- linear verification time: verifier는 다항식을 직접 계산해야한다.
- breaks zkness: 다항식 자체를 알게 된다.

우리가 살펴볼 scheme들은 아래의 개선이 있다.

- compressing: 다항식 계수 전체보다 commitment size는 작고 verification time도 감소한다.
- computationally binding: p(z)를 물어봤을 때 정말 polynomial을 아는 경우에만 “efficiently” 증명 생성이 가능.
- “efficiently”: 보통 linear 이하의 시간 의미. discrete logarithm problem을 풀거나 hash collision을 찾아 증명을 생성하는 것을 제외하기 위함.
- hiding: 다항식 자체는 공개하지 않거나 영지식성을 보장한다.

(ProofsArgsAndZK Ch14 207p)

## 성질

해당 commitment scheme이 다룰 수 있는 다항식 차수의 upper bound를 m이라고 하자. m은 준비된 trusted setup에 의해 결정된다.

- **binding**: commit 한 뒤 open하는 값은 반드시 다항식 p(x) 위의 한 점이다.
- **succinct**: The number of bits of commitment ≤ *log*(*m*)^*k*
- **hiding:** opening the committed polynomial at no more than *m* points
doesn’t reveal any extra information about the polynomial

(moonmath)

## 단계

1. setup
2. commit
1. Prover가 다항식을 바꿀 수 없게 p(x)의 commitment를 보낸다.
3. open
1. Verifier는 특정 x좌표 z에서의 다항식 값 p(z)를 보내라고 요청한다.
2. Verifier는 Prover가 아무 값이나 보낸 것이 아니라 정직하게 함수 p(z) 값을 주었는지 commitment를 이용해 확인한다.

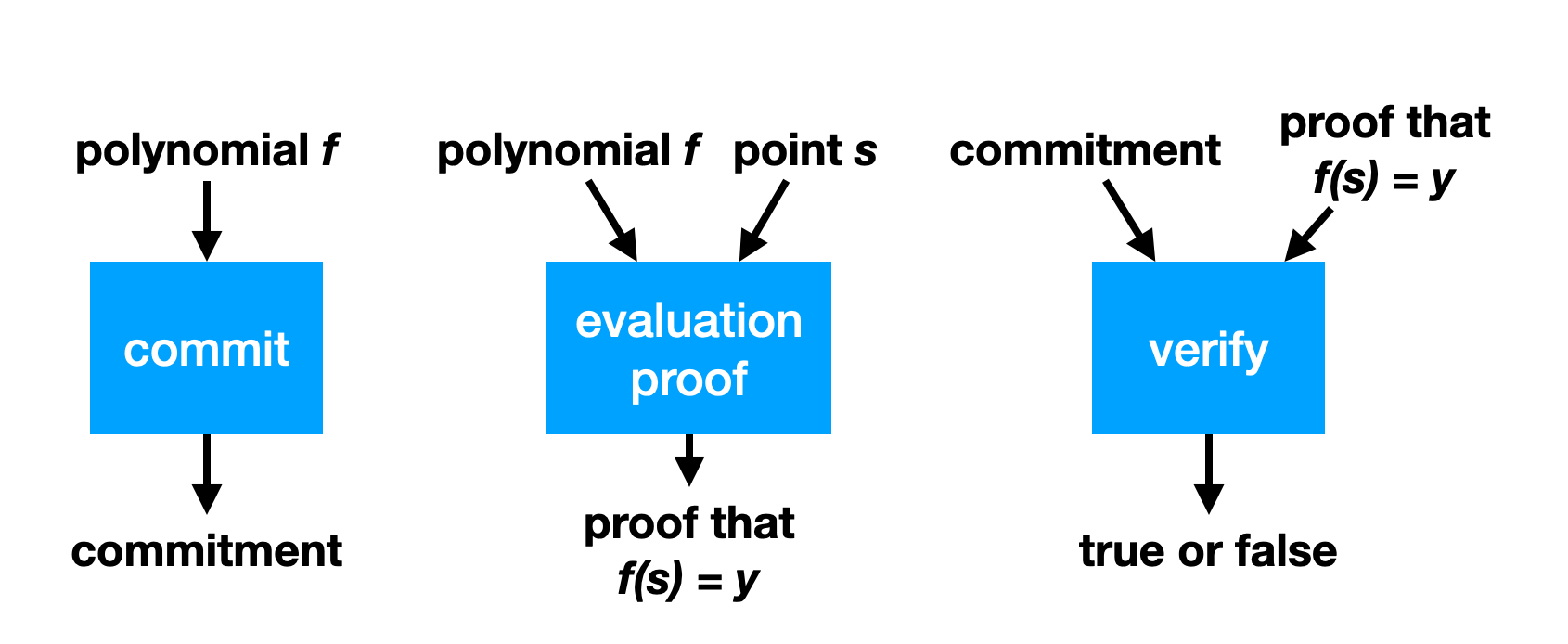
https://o1-labs.github.io/proof-systems/plonk/polynomial_commitments.html

## 종류
https://www.youtube.com/live/CsNoMKSh2e8?si=QJ9wlFge4p6F6RrT&t=1720

1. Pairing-based
1. 예시: KZG
2. Trusted setup 필요
3. elliptic curve, discrete logarithm problem 사용
2. IPA
1. 예시: Halo2
2. elliptic curve, discrete logarithm problem 사용.
3. https://arnaucube.com/blog/ipa.html
3. FRI
1. 예시: STARK
2. Trusted setup 필요 없음
3. discrete logarithm problem 사용 안 함. hash 함수 기반이므로 양자컴퓨팅으로부터 안전

오늘은 KZG만 다루자.

## Kate commitment

- Groth16, PLONK에서 사용됨.
- 최초 논문에서는 G_1 = G_2인 symmetric pairing이 사용되었으나 흔히 asymmetric pairing을 사용.
- 장점: 증명 크기가 제일 작음.
- 몇차 다항식인지 관계없이 한 점을 지난다는 것을 one group element로 증명. BLS12_381 기준 48 bytes.
- 단점: Trusted setup.
- 보완: 여러 명이 돌아가면서 $\{ 1, \tau g, \tau^2 g \}$ 를 $\{ 1, s (\tau g), s^2(\tau^2 g)$ 로 만듦으로써 $\tau = \tau \cdot s$ 로 업데이트. 한 명만 자신의 s값을 숨기면 최종 $\tau$ 를 알 수 없음. KZG ceremony에서 쓰인 방식.

Trusted setup에서 $g_1, \tau g_1,... , \tau^k g_1$을 준비하면, $P(x) = a_k x^k + a_{k-1}x^{k-1} + ... + a_1x + a_0$ 의 commitment C는 아래처럼 계산한다.

$$
C = P(\tau) g \\
= (a_k \tau^k + a_{k-1}\tau^{k-1} + ... + a_1\tau + a_0)g \\
= a_k (\tau^kg) + a_{k-1}(\tau^{k-1}g) + ... + a_1(\tau g) + a_0g
$$

### 증명 과정

p(z) = y 를 증명한다고 해보자.

표기

$e([a]_1, [b]_2) = e(G, H)^{ab} = [ab]_T$

$[a]_1 = aG, [b]_2 = bH$

과정

1. s는 trusted setup의 secret. s 는 toxic waste로 버리고 $G, [s]_1 = sG, [s^2]_1 =s^2G, ..., [s^m]_1 = s^nG$ 와 $[s]_2 = sH, ..., [s^m]_2 = s^mH$ 이 Trusted setup으로 공개된다. n은 다항식 p로 사용 가능한 최대 차수, m은 한 번에 증명 가능한 점의 개수를 제한한다.
2. Prover는 the commitment of the polynomial p(x) $C = [p(s)]_1$ 를 보낸다.
1. 예시: $p(x) = ax + b$ 라면, $[p(s)]=[as + b] = a(sG) + b(G)$
3. Verifier는 p(x) 값 계산이 필요한 랜덤 x 좌표, 즉 z 를 보낸다.
4. Prover는 $\pi = [q(s)]_1$ 와 계산값 p(z) (또는 y) 를 보낸다.
1. q(x): 다항식 나눗셈의 몫.
2. p(z) = y 를 증명하다면, $p(x) - y = q(x)(x - z)$
5. Verifier는 이 등식의 성립 여부를 확인한다. $e(\pi, [s - z]_2) = e(C - [y]_1, H)$
1. Schwartz-zippel lemma를 사용해서 x=s 에서만 $p(x) - y = q(x)(x - z)$ 의 성립을 확인함으로써 양변이 정의역 전체에서 같음을 증명한다.

Verifier의 검증 방법 풀이

$$
\begin{aligned}
e([q(s)]_1, [s]_2 - [z]_2) &= e([p(s)]_1 - [y]_1, H) \\
e([q(s)]_1, [s - z]_2) &= e([p(s) - y]_1, H) \\
e(G, H)^{q(s)(s-z)} &= e(G,H)^{p(s) - y}
\end{aligned}
$$

예시

$p(x) = x^2 + 3x$ 라고 하자

z = 3 이면, $p(x) - p(3) = q(x)(x - 3)$ 이므로 $x^2 + 3x - (3^2 + 3 \cdot 3) = q(x)(x-3)$

따라서, q(x) = x + 6 이고 $\pi = [q(s)]_1 = [s + 6]_1 = (s+6)G = sG + 6G$ 로 Trusted setup을 이용해 계산 가능.

### Correctness

절차를 따르면 통과하는 증명을 만들 수 있음

→ 위에서 증명 & 검증 과정을 보였으므로 만족.

### Binding

만약 Prover가 p(3) = 4 라고 증명하려고 하면 다항식이 나눠떨어지지 않는다.

$$
x^2 + 3x - 4/ (x - 3) = (x-1)(x+4) / (x -3)
$$

$(s - z)G$ 는 Prover도 아는 값. 여기서 $\frac{1}{(s -z)}G$ 도 구할 수 있는지가 중요.

이를 D-strong Diffie-Hellman (SDH) assumption 이라고 부른다.

> *D-strong Diffie-Hellman (SDH) assumption*, that essentially just asserts that “dividing in the exponent” by τ − *z* is intractable (ProofsArgsAndZK Ch15.2 233p)
>

이 가정은 discrete logarithm problem이 어려움을 전제한다.

만약 (s-z)G 에서 (s-z)를 구할 수 있다면 곱셈의 역수를 구하는 ax = 1 mod p 문제는 Extended Euclidean algorithm으로 풀 수 있다. 따라서 $1/(s-z), \frac{1}{(s -z)}G$ 의 순서로 계산 가능하다.

**Extended Euclidean algorithm**
a,b가 주어졌을 때 ax + py = gcd(a, p) 를 만족하는 정수 x, y를 계산해주는 알고리즘. p가 소수이면 gcd(a, p) = 1 이므로 ax = 1 mod p를 계산해주는데 사용할 수 있다.

직관적 이해: 등장하는 모든 수들을 ax + py 형태로 표현해서 마지막 gcd(a, p)까지 도달한다.
https://www.youtube.com/watch?v=IwRtISxAHY4

**만약 s가 유출된다면?**

s = 4 라는 사실을 Prover가 알고 있다고 가정해보자.

$p(4) = 4^2 + 3*4 = 28$

현재, $C = p(4) \cdot G = 28G$ 라는 commitment는 Verifier가 알고 있다.

악의적 증명자는 p(s) - y = q(s)(s-z) 만 만족하면 되기 때문에

28 - y = q(4) 를 만족하도록 q(4)를 설정한다면 원하는 대로 y값을 증명할 수 있다.

예를 들어 y = 10 을 원하면 [q(4)]_1 = 18G를 같이 보내주면 검증자는 p(4) - 10 = q(4)(4 - 3) 을 확인하고 통과시킨다. 즉, p(x) 를 지나지 않는 점을 verifier에게 보낼 수 있게 된다. Not binding!

### ZKness

위의 polynomial commitment scheme은 p(z) 값이 공개되는 것이라 완벽히 영지식은 아니다. 따라서 사용할 때 blinding factor라는 Prover만 아는 값을 추가함으로써 영지식성을 보장한다.

### The Power Knowledge of Exponent (PKoE) assumption
- The Power Knowledge of Coefficient assumption 이라고도 부름.
- Trusted setup에 Verifier만 아는 상수 $\alpha$ 배한 원소들을 추가.
- p(x) 가 다항식임을 보장하기 위함.
- proof와 $\alpha$ 배한 proof 두 개를 보내기를 요청.
- groth16에서는 이걸 안 해도 되게 만들어서 증명 개수를 피노키오의 12개에서 3개로 줄임. (조사 필요)

참고
- ProofsArgsAndZK 234p. An extractable scheme 파트
- https://electriccoin.co/blog/snark-explain3/

## Multiproof

두 점을 지난다는 것을 증명하려면?

방법1. 한 점을 지난다는 증명을 2번 한다.

방법2. $x = z_0$ 일 때 $y_0, x=z_1$일 때 $y_1$ 인 다항식과 $(z_0, y_0), (z_1, y_1)$ 에서 만난다고 한 번 증명

과정

1. 분자는 Lagrange interpolation 한 다항식으로 빼고
2. 분모는 지나는 점들을  $(x - z_0)…(x - z_{k - 1})$ 으로 나눠 떨어짐을 보여 증명할 수 있음.

$$
\begin{aligned}
I(X) &= \sum_{i=0}^{k-1} y_i \prod_{j=0 \atop j \neq i}^{k-1} \frac{X-z_j}{z_i-z_j}
\\
Z(X) &= (X-z_0) \cdot (X-z_1) \cdots (X-z_{k-1})
\end{aligned}
$$

한 점을 지난다는 증명과 유사하게 다항식 나눗셈의 몫 q(x) 를 구하자.

$$
q(X) = \frac{p(X) - I(X)}{Z(X)}
$$

이를 x=s에서 평가한 q(s)를 타원곡선의 generator에 곱해서 증명을 생성한다. 즉 $\pi = [q(s)]_1$.

장점: 여러 점을 지남도 one group element(타원곡선 위의 점 하나), 48 byte로 증명.

예시

QAP에서 제약식의 개수가 곧 증명할 점의 개수가 되므로 여러 점을 한 번에 증명하기 위해 사용된다.

### 참고

- ProofsArgsAndZK Ch14 207p, Ch15.2
- https://dankradfeist.de/ethereum/2020/06/16/kate-polynomial-commitments.html
- https://cryptologie.net/article/525/pairing-based-polynomial-commitments-and-kate-polynomial-commitments/