# Алгоритми на матрицях
Ці алгоритми всі використовують матрицю --- двовимірний масив (як в numpy) або список списків (нативно в Пайтоні).
Іноді можна реалізувати матрицю як список рядків (але це для випадків, коли цю матрицю не потрібно буде змінювати в процесі).
В задачах (якщо не сказано іншого) потрібно **повернути** нову матрицю, а не змінювати матрицю на вході.
## Створення матриці
Створити матрицю NxM елементів, яка складається з нулів.
```python=
In [12]: gen_matrix(10, 5)
[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
```
Уважно при створенні! Зміна одного елементу матриці не повинна призводити до зміни інших елементів!
## Зробити копію матриці
Це може здаватись просто, але це не так просто як здається.
```python=
matrix = gen_matrix(10, 5)
print(matrix)
# [[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
new_matrix = matrix # чи працює це як копіювання?
matrix[0][0] = 10000000
print(matrix)
# [[10000000, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
print(new_matrix)
# [[10000000, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
```
Звісно, можна використати `copy.deepcopy()`, але так не цікаво. Цікаво розібратись чому просте присвоєння не працює і як це обходити.
## Віддзеркалення матриці
Реалізувати горизонтальне та вертикальне віддзеркалення матриці
```python=
matrix = [
[0, 0, 0, 0, 0],
[0, 1, 2, 3, 4],
[0, 2, 4, 6, 8],
]
print(vert_flip(matrix))
# [[0, 2, 4, 6, 8],
# [0, 1, 2, 3, 4],
# [0, 0, 0, 0, 0]]
print(horizontal_flip(matrix))
# [[0, 0, 0, 0, 0],
# [4, 3, 2, 1, 0],
# [8, 6, 4, 2, 0]]
```
## Транспонування матриці
Транспонування матриці --- це віддзеркалення по діагоналі.
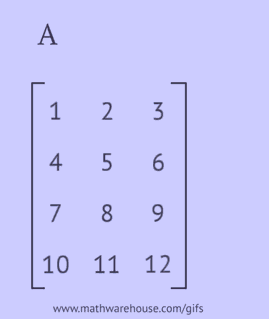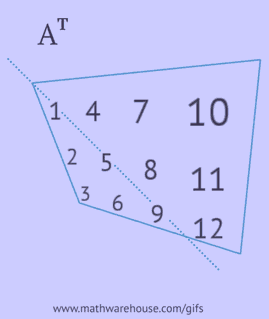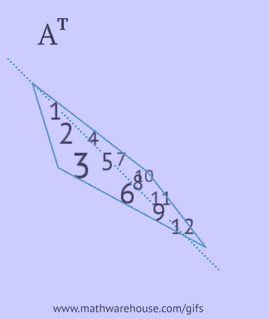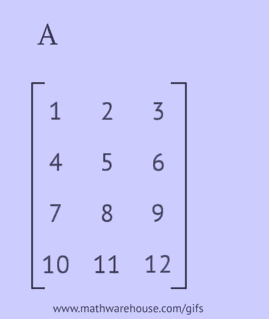
Реалізувати.
```python=
matrix = [
[0, 0, 0, 0, 0],
[0, 1, 2, 3, 4],
[0, 2, 4, 6, 8],
]
print(transpose(matrix))
# [[0, 0, 0],
# [0, 1, 2],
# [0, 2, 4],
# [0, 3, 6],
# [0, 4, 8]]
```
## Поворот матриці
Реалізувати поворот матриці на 90 градусів (в обидві сторони).
Підказка: поворот матриці можна зробити через комбінації транспозицій та віддзеркалень!
Підказка 2: поворот в одну сторону можна реалізувати через повороти в іншу сторону!
```python=
matrix = [
[0, 0, 0, 0, 0],
[0, 1, 2, 3, 4],
[0, 2, 4, 6, 8],
]
print(rotate_left(matrix))
# [[0, 4, 8],
# [0, 3, 6],
# [0, 2, 4],
# [0, 1, 2],
# [0, 0, 0]]
print(rotate_right(matrix))
```
## Порахувати кількість ненульових елементів матриці
```python=
matrix = [
[0, 0, 0, 0, 0],
[0, 1, 2, 3, 4],
[0, 2, 4, 6, 8],
]
print(nonnull_count(matrix))
# 8
```
## Алгоритми класичного Тетрісу
### Копіювання матриці в матрицю
В комп'ютерній графіці є термін під назвою `blit`, який означає копіювання пікселів картинки в певну точку екрану.
Потрібно реалізувати це ж, але для машої матриці.
В Тетрісі ігрова дошка задається як матриця, а фігурки задаються як маленькі матриці. Тому щоб поставити фігуру на дошку потрібно скопіювати матрицю фігурки в матрицю дошку в певну координату.
### Накладання елементів
Для перевірки колізій в Тетрісі потрібно спробувати скопіювати матрицю фігурки в матрицю дошки, і якщо хоча б в одному місці буде "колізія" (накладення), то це означає неможливість подальшого руху.
На фігурку діють 2 сили --- гравітація, яка рухає вниз, і гравець, який може рухати в обидві сторони (і вниз). Щоб перевірити чи фігурку можливо рухати в сторону або вниз, потрібно:
- скопіювати поточну дошку
- спробувати поставити фігуру в напрямку руху (на 1 клітинку правіше, лівіше, або нижче)
- якщо колізії не було, то продовжувати гру
- якщо була колізія, то заборонити рух в цю сторону
- якщо колізія сталася при русі вниз, то це означає що фігурка досягля низу
- а отже, потрібно зафіксувати поточне положення фігурки на дошці
## Алгоритми 2048
### Випадковий елемент
Потрібно згенерувати у випадковому місці матриці 4х4 число --- з ймовірністю 75% число 2, і з ймовірністю 25% число 4.
Важливо, що випадково згенероване число не повинно накластись на уже існуюче число в матриці.
### Свайп
Реалізувати "свайп" в одну зі сторін.
Свайп в інші сторони можна реалізувати через поворот дошки в "зручну" сторону, свайп, а потім поворот дошки назад.
## Алгоритми Powder Toy
https://www.youtube.com/watch?v=VLZjd_Y1gJ8&list=LL&index=1&ab_channel=JohnJackson
{%youtube VLZjd_Y1gJ8%}
## Алгоритми в шахах
### Які поля під ударом
Для кожної фігури (король, ферзь, слон, тура, кінь, пішак) отримати список полів, які знаходяться під ударом цієї фігури, якщо відома координата фігури.
### Блокування ходу
У всіх фігур (окрім коня) хід може бути обмежений через наявність фігур на лінії ходу (своїх або чужих). Отримати список можливих полів для ходу з врахуванням цих перешкод.
### Перевірка шаху, пату і мату
Перевірити, чи для король знаходиться під ударом суперника (шах) і чи може король зробити хід (пат, якщо не може) не потрапивши під удар іншої фігури. Якщо одночасно шах і пат, то це мат.
## Алгоритми Го
### Захоплення території
Написати алгоритм, який визначає чи територія захоплена (і яка саме територія).